基于AHP-TOPSIS的山区低等级公路路面破损评价方法

裴玉龙，常 铮，金英群

(东北林业大学 交通学院，黑龙江 哈尔滨 150040)

2019年9月中共中央、国务院印发了《交通强国建设纲要》，明确提出要形成广覆盖的农村交通基础设施网。我国是一个多山的国家，山区面积占全国总面积的2/3，因此，做好山区公路研究是实现交通强国的必要基础。目前对山区公路路面平整度的评价主要有加权纵断面评价方法(WLP)[1]、弯沉检测法[2]和基于SVM的路面性能评价[3]等评价方法，而且大多适用于高等级公路，计算方法一般相对复杂，对山区低等级公路路面平整度的评价适用性不强。山区公路的路面破损一般分为路面开裂、路面坑槽和车辙破损等多种类型[4]，每种破损类型的危害程度都有所不同，通常特定的原因都会导致固定的路面破损类型，因此在评价路面破损指数时，可先确定各类路面破损危害性的权重，进而计算出每条路面的破损指数。本文拟采用AHP法来逐层分析道路破损的原因，并计算出各类原因危害性的权重，将权重值带入到TOPSIS模型中，计算出各路段的路面破损指数，将指数进行排序，指数越高路段的路面破损越严重。此模型计算简便，且数据容易获取，可最大限度地降低由主观臆断造成的误判，可在山区低等级公路路面平整度评价方面提供相对准确的参考。

1 基于AHP-TOPSIS的山区公路路面评价模型

山区低等级公路路面破损指数是对山区低等级公路路面破损程度的定量评价指数，按照道路交通系统构成，可将导致山区公路路面破损的原因按照环境因素、人与车的因素和道路自身因素分为三部分：环境因素包括动植物的影响、山体滑坡、雨水冲刷[5]和环境温差[6][7]；人与车的因素包括车辆超载超重[8]、山区农民因耕种等行为而对公路造成的人为破坏；道路自身因素包括路面的自然收缩与沉降[9][10]。基于此，可建立山区低等级公路路面破损原因的层次结构模型，如图1所示。

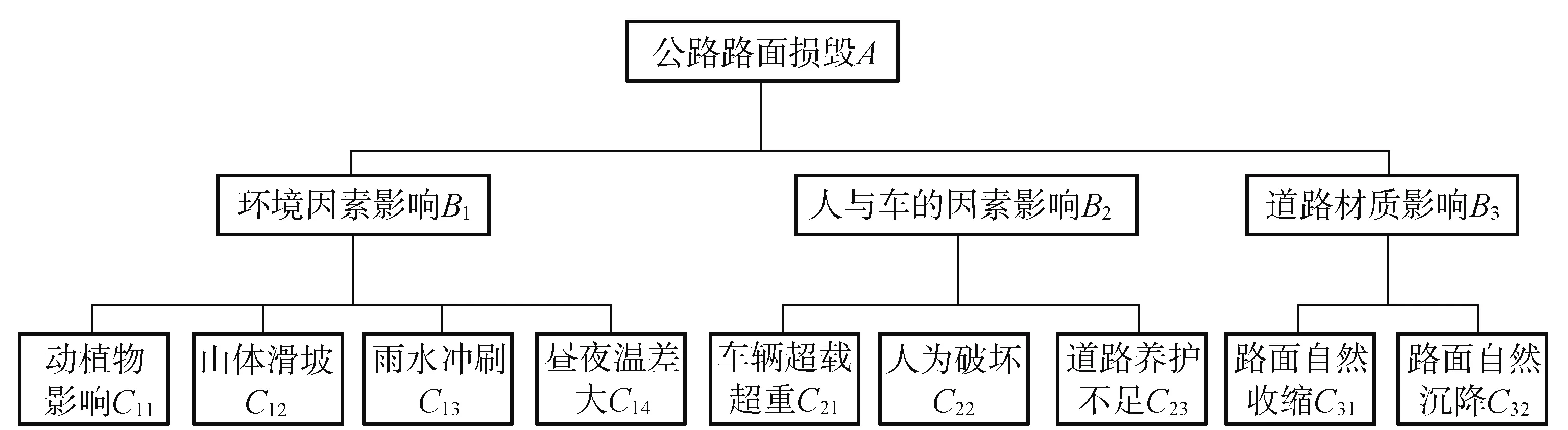
图1 山区低等级公路路面破损层次结构模型

1.1 基于AHP的不同类型路面破损危害性权重计算

1.1.1 标度方法

层次分析法(简称AHP法)是由美国运筹学家T.L,Satty等人在20世纪70年代初提出的一种定性与定量分析相结合的多准则决策方法[11]，比较适合解决交通安全评价这类层次性和模糊可变性较强的问题[12]。其评价指标的主要依据是两两比较标度，并利用二元对比法对同层次的两个评价指标进行比较及赋值，采用数字1～9作为标度来定义判断矩阵A=(aij)n×n，如表1所示[13]。

表1 判断矩阵标度

1.1.2 构造不同类型路面的破损危害性矩阵

根据图1所示信息，可参照表1所述重要度指标、按式(1)逐层构造不同类型的路面破损危害性判断矩阵

(1)

1.1.3 权重计算及一致性检验

运用AHP法计算不同类型的路面破损危害性权重向量的方法有四种，因四种方法计算得出的数值一般情况下都比较接近，故本文采用算数平均法计算权重向量，如式(2)、式(3)所示

(2)

(3)

在得到不同类型的路面破损危害性权重向量后，为验证判断矩阵是否合理，需要对矩阵进行一致性检验，检验方法如式(4)所示

(4)

当CR<0.10时，可认为判断矩阵的一致性是可接受的，否则要对矩阵做适当修正。一致性指标如表2所示。

表2 一致性指标

1.2 基于AHP-TOPSIS的路面破损模型

1.2.1 建立路面破损指数初始评价矩阵

逼近理想解排序法(简称TOPSIS)是由Hwang和Yoon于1981年首次提出的一种有限方案多目标决策的评价方法[14]，能够对评价对象与理想目标的接近程度进行合理排序[15]，在进行山区低等级公路路面评价时，可利用TOPSIS模型来计算公路路面破损指数。设待评价的路段集为R={R1,R2,…,Rn}，各路段的评判指标为图1所示路面破损的9种类型，评价指标rij表示第i条路段的第j种路面破损类型(其中i∈[1，n]，j∈[1，9])，如式(5)所示

(5)

1.2.2 建立AHP-TOPSIS路面破损指数加权评价矩阵

评价矩阵中各评价指标所对应的数值为不同类型的路面破损数量，其中单个类型的破损数量越多说明路面破损越严重。将2.1.3中运用AHP法得到的权重向量W与矩阵R的列向量相乘，即可获得基于AHP-TOPSIS模型的加权评价矩阵Bij=(bij)，如式(6)所示，将矩阵B利用式(7)进行归一化处理，得到归一化矩阵

(6)

(7)

1.2.3 路面破损指数计算

在本文所述的模型中，路面破损指数的数值用待评价路段各指标数值与最优解的贴近程度来表示，单个指标数值越大，表示此种类型的路面破损数量越多，因此该模型的最优解D+为矩阵P=(pij)列向量的最大值，最差解D-为矩阵P=(pij)列向量的最小值，其计算方法如式(8)、式(9)所示

D+=(maxmpmn).

(8)

D-=(minmpmn).

(9)

待评价路段各指标数值与最优解贴近程度的计算方法如式(10)、式(11)所示

(10)

(11)

根据上述计算，可得山区低等级公路路面的破损指数计算式为

(12)

如果待评价路段与最优解相同，则贴近度为1，如果待评价路段与最差解相同，则贴近度为0。由此可见山区公路路面破损越严重，路面破损指数越高，因此，将路面破损指数由大到小排列，路面破损指数最高的公路路面损毁最严重。

2 案例应用

贵州榕江县某山区路面破损严重，经调查人员的实地考察，得到3条待评价公路路面的破损情况，如表3所示。

2.1 构造判断矩阵并分配不同种类路面破损危害性权重

根据第二段图1所示的层次结构模型，运用德尔菲法[16]获得设计单位工作人员及专家对各类路面破损原因危害性的反馈结果，建立如表4～表7所示的判断矩阵。

表3 待评价山区公路路面破损情况

表4 Bi判断矩阵

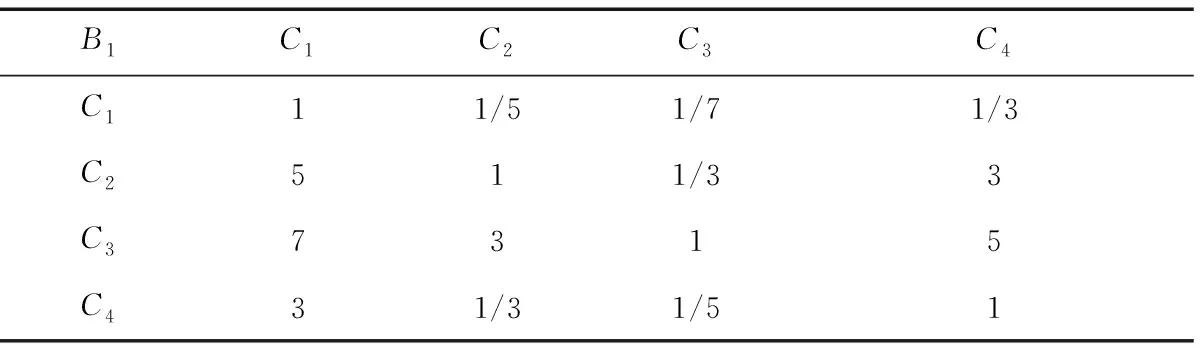
表5 C1j判断矩阵

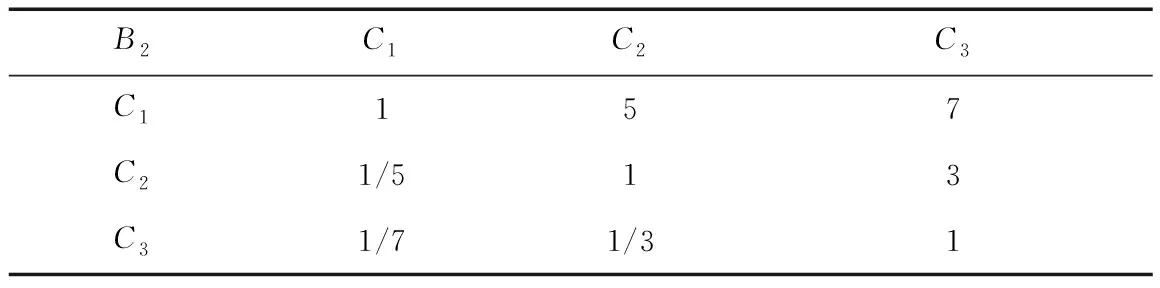
表6 C2j判断矩阵

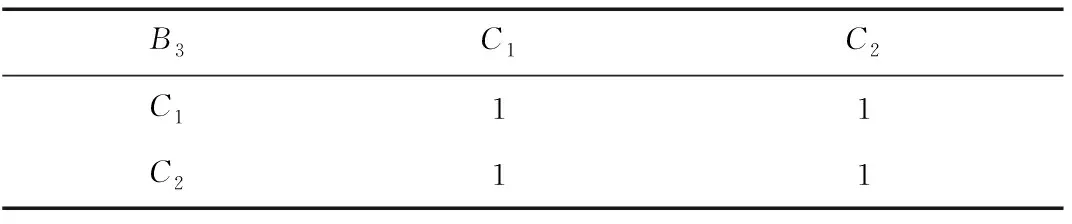
表7 C3j判断矩阵

将表4列向量按式(2)、式(3)计算，得出不同种类路面破损危害性的特征向量WA及AWA

最大特征值

一致性比例

CRB1=0.044，CRB2=0.063，CRB3=0.

一致性检验所得结果均小于0.1，因此，以上矩阵均通过了一致性检测，具有令人满意的一致性，进而得到山区低等级公路不同种类路面破损的危害性权重，如表8所示。

表8 山区低等级公路不同种类路面破损危害性权重

2.2 路面破损指数的计算

根据表3所示的待评价公路路面破损情况，由式(5)、式(6)、式(7)可得到三条公路的路面破损情况是基于AHP-TOPSIS的归一化矩阵

根据式(8)、式(9)可计算出待评价的三条公路所构成的模型最优解和最差解分别为

D+=(0.811 1 0.681 0 0.768 2 0.577 4 0.696 0 0.820 8 1 0.813 7 0.7493)，D-=(0.324 4 0.425 6 0.384 1 0.577 4 0.464 8 0.164 2 0 0.348 7 0.46 83).

根据式(10)、式(11)计算路段1各指标与最优解和最差解之间的距离为

根据式(12)计算出各路段1的路面损毁指数Ei为

同理，可计算出路段2与路段3各指标与最优解和最差解的距离，及其路面损毁指数，如表9所示。

表9 山区公路路面损毁评价结果及排序

根据表8可知，路段2的路面破损指数为0.728 1，在3个路段中路面破损程度最高，因此，应着重对路段2进行养护与修复。

3 结束语

本文根据山区公路里程长、等级低的特点，提出了公路路面破损指数的概念，并引入了AHP-TOPSIS模型对公路路面破损指数进行计算，克服了传统公路路面评价方法只适用于高等级公路、且计算过程相对繁琐的缺陷。该模型仅依靠简单的数据便可对山区低等级公路路面做出相对客观的评价，同时也避免了传统方法在山区公路路面评价时由专家的主观臆断所造成的误判。所得结果可为山区低等级公路的养护工作提供有效数据参考，该方法也可推广至山区公路路基评价，进而为我国山区低等级公路建立更加完善的评价体系。