基于客流加载的城市轨道交通网络关键点分析

巨玉祥，李文霞，李 卓，何晓平，陈晓明

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

城市轨道交通作为交通系统的骨干及城市规模较大地区的主要交通出行工具,其系统化发展和网络化运营为城市居民的出行带来了极大便利,在很大程度上缓解了大型城市的交通拥挤和交通压力。城市轨道交通高密度、高频率的运营优势,同时也带来了防护设施及通道应急薄弱的运营特点,尤其是当部分重要站点和区间出现突发事件，会对全网产生级联失效影响(即某一节点受到破坏后向全网传播的速度)[1]。网络化运营的模式加强了车站之间的关联度，同时由于车站客流分布的差异化，使车站的重要程度也出现了较大程度的分化[2-3]。因此，借鉴科学成熟的理论研究方法并结合轨道交通网络的运营实际，准确有效地识别出重要节点，对提高系统运营的安全性及优化网络布局具有十分重要的意义。

复杂网络是研究城市轨道交通网络运营特性的重要方法之一，网络节点中心性的研究也是其主要应用。刘志谦[4]等基于space L方法对广州地铁网络拓扑建模，对节点的度、聚类系数、平均路径长度等指标的分布规律进行了探究，并对换乘车站故障情况下的网络可靠性进行了深入研究；Xingtang Wu等[5]提出一种优化换乘次数和旅行距离的乘客出行主观策略，以此评价网络的结构效率，并引入一种称为“节点占用概率”的中心度来评估站台利用率；李倩[6]结合城市轨道交通网络特性综合考虑节点的局部属性、全局属性及连通属性，建立了6个相关指标，并运用变异系数法和TOPSIS法对节点进行重要度排序。以上研究内容所建立的指标从网络自身结构属性及网络整体连通等角度对节点重要度进行评估，如节点的度(与该节点相连的边数)侧重反应节点的连通性，节点的邻近中心性(给定节点到网络中其他节最短距离之和)侧重反映节点在网络全局的可达性，这些指标具有不同的侧重，且已有研究并未提出节点综合中心性测算方法，即从节点的连通性、可达性及枢纽能力等方面进行综合评价[7-9]。

既有研究对客流加载条件下的网络节点重要度相关研究也较少。在客流分配方面，黄鉴等[10-11]分析了网络中弧阻抗的计算方法，提出了城市轨道交通客流平均分配模型。在节点重要度评估方面，裴玉龙等[12]构建基于相邻站点的多模式拓扑网络模型，基于复杂网络理论对多个结构特征指标值进行分析；胡映月等[13]分析了不同类型车站的运输特点，构建了客流传播模型，基于复杂网络理论提出了4个评价指标；陈培文等[14]通过建立网络客流分配模型，结合AFC数据对网络客流聚集程度和客流中心性进行分析，提出客流驱动下网络的特性会发生显著变化，但仅对客流进行单一路径的全有全无分配，这与网络客流多进路分布的运营实际有较大出入。

综上所述，为改进已有研究中单个指标评价的片面化，便于决策者进行全局性决策，基于城市轨道交通的网络物理拓扑结构，考虑网络的不同换乘方式，从用户均衡原则出发，将全网客流进行分配，对网络客流进行加载，对客流加载条件下城市轨道交通网络节点重要度进行定义。同时，进一步分析客流加载条件下各指标与客流量的关联性，提出节点综合重要度计算方法，从网络全局出发对节点的重要性进行评价。最后，以北京地铁网络为例，验证该方法的有效性。

1 城市轨道交通网络客流分配模型

从城市轨道交通网络的结构特性出发，基于经典space L模型，建立城市轨道交通网络模型，将城市轨道交通网络中的不同车站抽象为网络中的节点，将不同车站间的运行线路抽象为节点间的连接边，基于此得到城市轨道交通拓扑网络是一个复杂网络，该网络的数学表达式为G=(V,E)，其中V=(v1,v2,…,vn)表示网络中所有节点的集合，E=(e1,e2,…,em)表示网络中所有边的集合。

1.1 阻抗函数的确定

建立模型对城市轨道交通网络进行客流分配是分析客流加载条件下网络节点重要度的前提，通过客流分配将网络全局客流分配到不同OD对的不同线路中，进而得到不同线路的客流数据，并将所分配的客流数据引入到指标构建中。在构建网络拓扑结构的基础上，建立客流均衡分配模型，关于阻抗函数的计算在此借鉴文献[8]的内容。

1.1.1 运行弧阻抗

运行弧阻抗包括区间运行时间和高峰期内车站客流量急剧增大带来的拥挤换算时间。其中区间运行时间以相邻车站间的平均运行时间和列车在站、停站时间之和来表示。

Te=tt+tsp，∀e∈E1.

(1)

式中：Te为区间运行时间，tt为列车区间平均运行时间，tsp为列车在出发站台的停站时间。

拥挤换算时间是指车站高峰期时间段由于大量客流的涌入给乘客带来的不适感产生的额外时间。当在车乘客数小于列车座位数时，乘客不会感到拥挤；当在车乘客数大于列车座位数、而小于列车定员数时，会产生一定的不适感；当在车乘客数大于列车定员数时，由于过度拥挤不适感会增强。

(2)

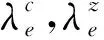
综上所述，运行弧的总阻抗计算公式为

Re=Te·[1+Ce(c)]，∀e∈E1.

(3)

1.1.2 换乘弧阻抗

换乘弧阻抗由换乘走行时间和换乘等待时间组成，换乘走行时间为乘客在换乘通道内的走行时间，换乘等待时间由换乘线路上平均发车间隔决定，通常取发车间隔的1/2[10]，同时由于乘客在换乘走行过程中会消耗体力，因此，对旅客由于换乘而带来的时间消耗乘以惩罚系数，将时间进行放大。

Re=ε·(tw+Il/2)，∀e∈E2.

(4)

式中：ε为换乘惩罚系数，tw为换乘走行时间，Il为换乘线路列车的平均发车间隔。

1.1.3 关联弧阻抗

关联弧阻抗仅表示车站与换乘站之间的关系。为避免在最短路搜索时将关联弧作为最短路，此处将关联弧阻抗取为一个较换乘弧大的实数M,避免将客流分配到关联弧。

Re=M，∀e∈E3.

(5)

1.2 客流分配模型及算法

对客流加载条件下的网络节点重要度进行分析,首先需要将客流在全网进行分配,通过对近年来在道路交通路网客流分配中发展较为成熟的Frank wolfe算法进行改进,将客流在全网进行均衡分配[15]，进而构建出符合实际且有效的测度指标。

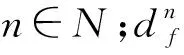
(6)

(7)

(8)

(9)

上述模型满足Wardrop(用户均衡)条件， 即将网络全局客流量分配后，各个路径阻抗相等且等于最短路径阻抗。利用matlab软件编程，进行frank Wolfe算法搜索，对模型进行求解。

2 城市轨道交通网络节点重要度评价指标

2.1 网络节点重要度指标构建原则

目前，城市轨道交通呈现出网络化运营状态，使线路间所承担的客流量产生明显差异，导致车站的客流承载压力出现分化、网络的异质性增强，因而，仅从网络的物理状态出发，对城市轨道交通网络中的节点进行评估，与网络运营实际不相符。因此，基于经典的网络中心性评价指标，考虑网络运营实际，将客流在全网进行分配，对客流加载条件下节点重要度的综合测度指标进行深入定义。所构建的三个指标中，节点承载压力STi反映节点客流出行需求对基础设施的局部压力，即从节点本身的属性出发，反映其在网络中的连通程度，STi值越大，则与该节点衔接的区间客流输送压力越大；节点服务水平NSLi从客流出行的角度得到节点在网络中的可达性与便捷性，侧重于反映节点在网络全局中的重要度；节点加权介数BKi从分方向换乘客流量差异性的角度出发，考虑节点在网络中的连通能力与枢纽作用，侧重于反映节点的区域重要度。当节点的物理网络属性与客流属性同时达到最优时，该节点才可定义为关键节点。

在构建网络拓扑结构过程中，针对节点加权介数指标，将网络中的换乘站台转化为分方向的换乘节点，针对节点承载压力与节点服务水平两个指标，将换乘站各站台节点整合，视为一个超节点，换乘枢纽抽象超节点如图1所示。

图1 换乘枢纽抽象超节点示意图

2.2 节点承载压力

节点承载压力的定义综合考虑网络的物理属性及客流属性，其中物理属性以节点度的物理意义为基础，节点的度描述为与节点i直接相连的节点个数，该指标反映了节点在全局的连通性，客流属性考虑节点间的断面客流量，以复杂网络中节点客流强度与节点度的比值来表示节点承载的压力STi，从节点自身的客流属性出发，反映其在网络中的重要程度。

(10)

式中：pij为节点i与节点j之间的断面客流量，Ki为节点的度。

2.3 节点服务水平

节点服务水平的构建综合考虑网络的客流属性与物理拓扑属性，其中客流属性考虑该节点的客流权重(单OD对间的客流量与所有OD对间总客流量的比值)，网络物理属性考虑所有OD对间旅行距离，以二者的乘积来刻画节点服务水平，其中旅行距离考虑OD对间实际最短路径距离，同时将由于换乘带来的旅行时间增加转换为等效时间内的旅行距离，该指标从整个网络层面评估客流条件下节点的服务水平，能够更有效反映节点的服务能力。

(11)

式中：NSLi为节点服务水平；dij为节点i到节点j之间的最短路径长度；m为节点i到节点j之间最短路径上需要换乘的次数；θ为换乘的路径距离放大系数，取0.2[11]；λij为0-1变量，若车站i到车站j之间最短路径上需要换乘，取值为1，否则为0；n-1为网络规模。

2.4 节点加权介数

该指标的构建同时考虑网络物理拓扑结构属性和客流属性，为定义该指标，首先对传统中心性指标中的介中心性进行解释。介中心性定义为路网中所有OD对间最短路径经过指定节点的次数，物理拓扑结构中位于网络中心位置的节点介中心性最高，该指标反映节点在网络全局的衔接能力。为在介中心性这一物理指标中加载客流属性，在此，考虑换乘枢纽内各换乘站台的客流量，提出节点加权介数，该指标定义为该换乘枢纽不同换乘方向上的客流权重(换乘站台客流量与该换乘枢纽总客流量的比值)与各换乘站台介中心性的乘积求和，体现了该节点在网络中的纽带作用，也即连通能力。

(12)

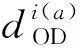
3 网络节点综合重要度计算方法

为得到节点综合重要度计算公式，需对上述三个指标间的内在联系进行分析，通过对上述指标的定义可知，节点服务水平和节点加权介数侧重反映了节点在网络全局的可达性及便捷性，是旅客出行路径选择的重要指标，而节点的承载压力也进一步反映了节点在网络中的连通性，在网络化的运营中节点的连通性是网络进行客流输送的基础保障，在网络中该指标的重要性是其他指标带来的优势所不能替代的。综上所述，采用多目标决策的组合规则[10]，得到节点承载压力与节点服务水平、节点加权介数为乘积关系，同时节点服务水平与节点加权介数相互独立且线性互补，因此是加法关系，得到节点综合重要度计算公式为

SIDi=STi·(ω1·NSLi+ω2·BKi).

(13)

为得到上述三个指标的内在联系，采用SPSS软件分别分析其与客流量的相关性，选取2016年11月3日，北京地铁7—9月早高峰地铁AFC刷卡数据，得到客流发送量，通过数据分析可得节点承载压力、节点服务水平、节点加权介数与客流量的相关性分别为0.312、0.542、0.580，即分别为中度相关、强相关、强相关。为确定ω1、ω2的权重值，参考节点服务水平、节点加权介数两个指标值与节点客流量的Pearsong相关性系数，同时考虑旅客换乘活动对节点加权介数重要度的影响，对相关系数进行修订，确定ω1=0.48，ω2=0.52。

4 算例分析

4.1 客流分配

为进一步验证所建立指标的正确性，并方便计算，选取以北京地铁1号线、2号线、4号线、5号线、10号线、13号线所组成的地铁网络拓扑结构图进行实例验证，构建得到北京地铁1、2、4、5、10、13号线组成的地铁网络拓扑结构，如图2所示。为便于表述，图中只列出各换乘站和线路上的主要车站。

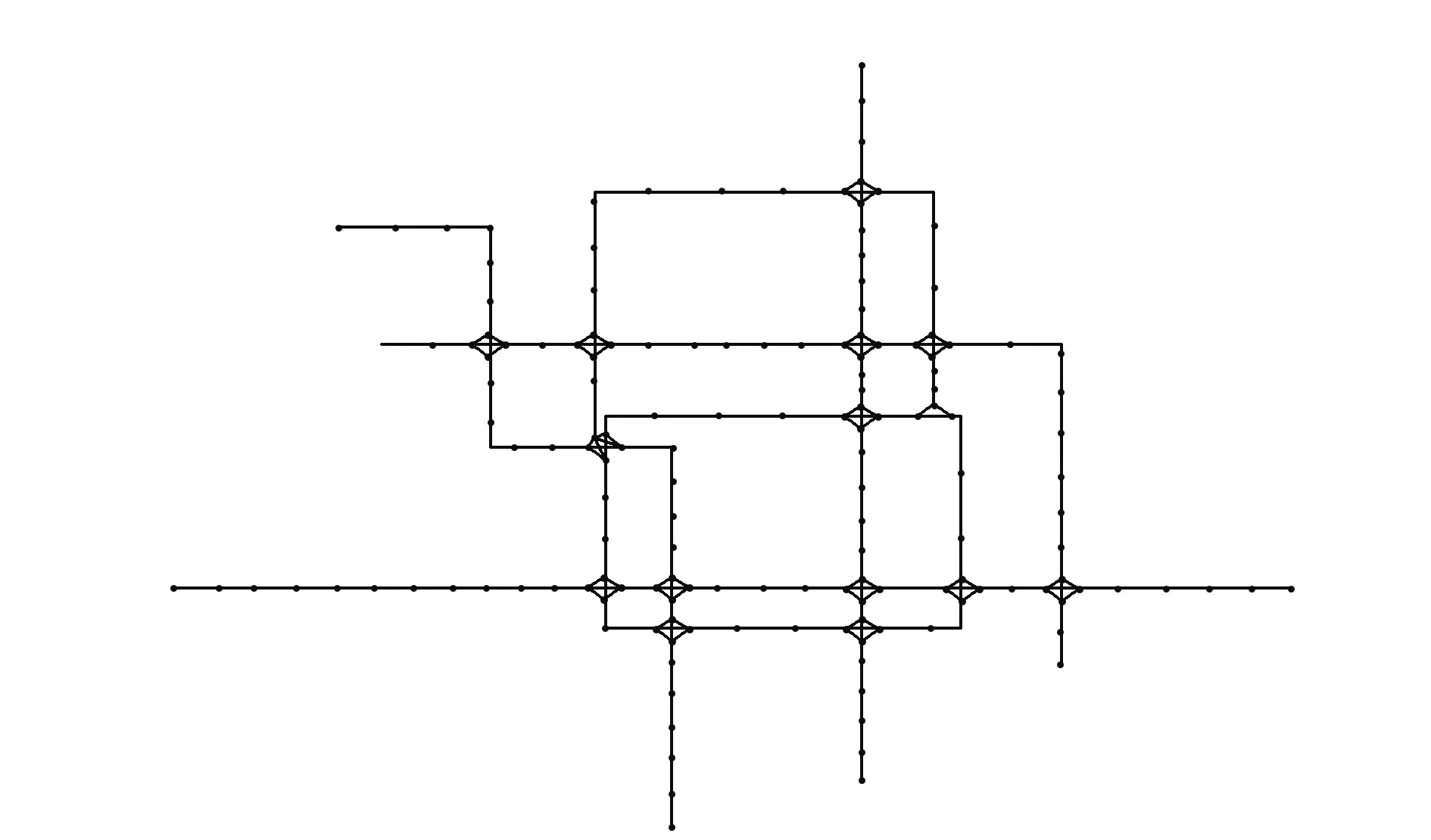
图2 北京地铁1、2、4、5、10、13号线组成地铁网络

首先对构建的北京地铁网进行客流均衡分配。选取2016年6月13日北京地铁该网络中各车站工作日全天OD客流数据，为降低计算难度假定OD客流矩阵对称。为进一步对客流进行分配，结合客流分配模型，对frank Wolfe算法各待定参数进行标定[10]，定义如下：平均发车间隔Il为3 min；列车服务频率fl.e为20对/h；列车定员为2 300人；列车标准座位数c为340人；列车平均停站时间tsp为40 s；拥挤校正系数α=1.2，β=1.8；换乘惩罚系数ε为1.5；换乘平均走行时间tw为3 min。根据用户均衡配流的frank Wolfe算法，选择MATLAB软件进行编程求解，得到各换乘站及站内各换乘站台客流量,如表1所示。

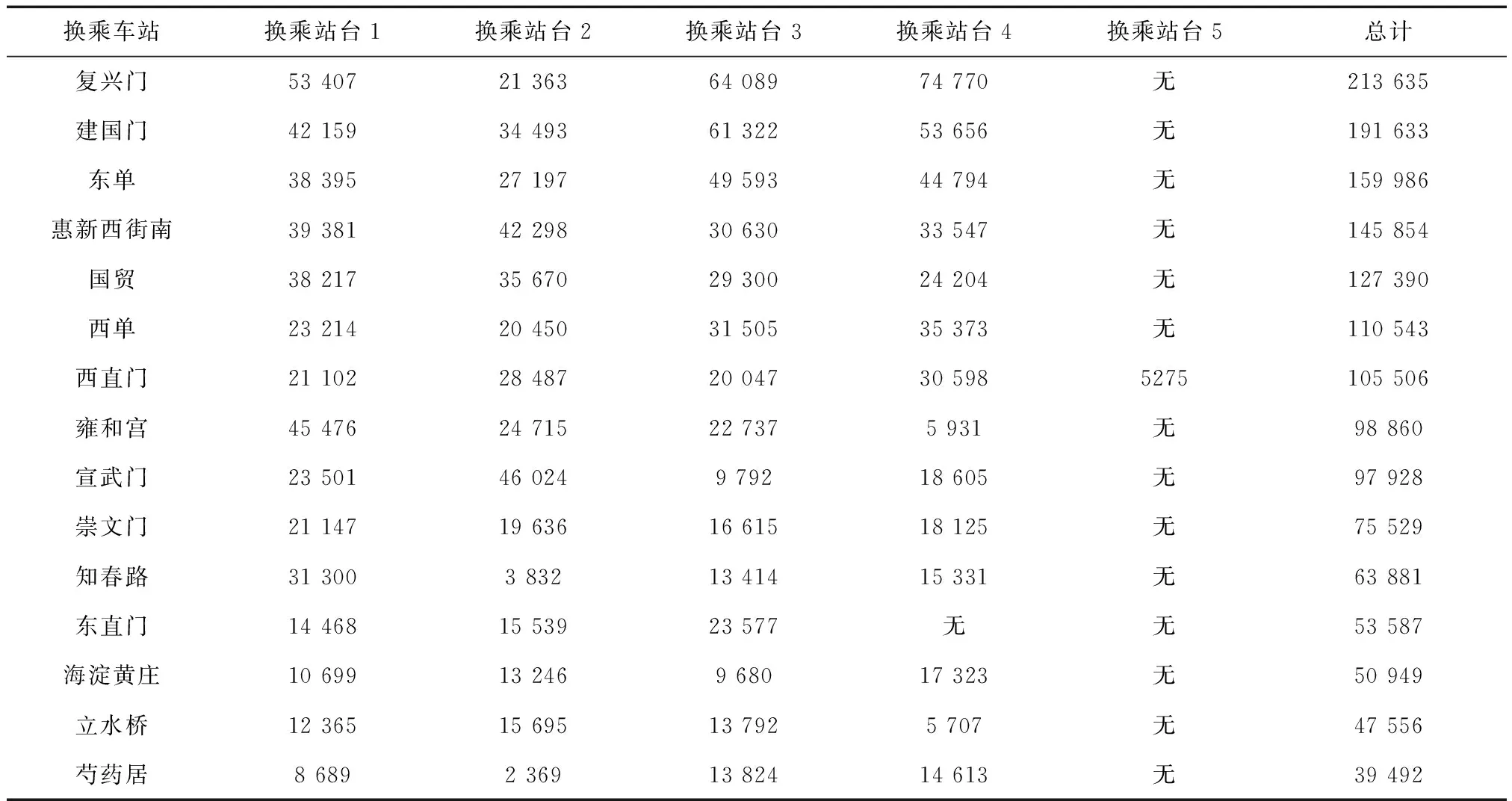
表1 各换乘站及站内各换乘站台客流量 人次

4.2 节点重要度分析

根据表1客流分配的数据结果，结合构建的客流加载条件下各指标值定义，计算得到各换乘车站标准化后的节点承载压力、节点服务水平、节点加权介数及节点综合重要度指标，如图3所示。

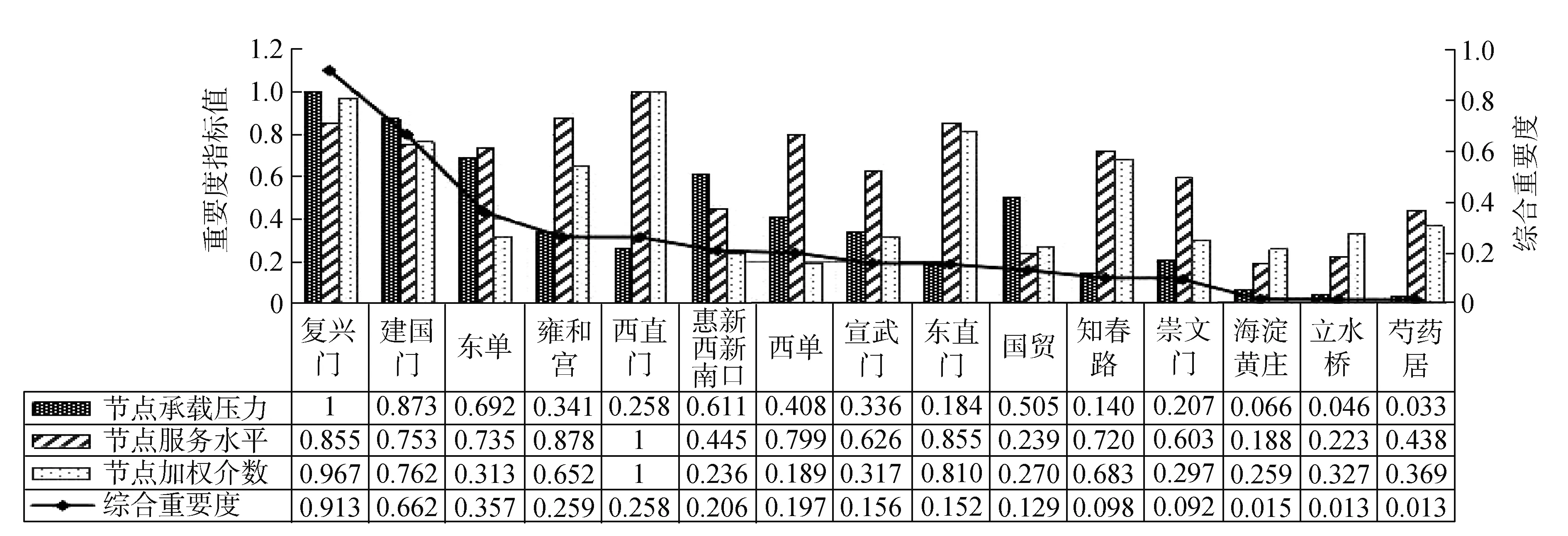
图3 各换乘站重要度指标对比

由图3 可知，综合重要度排名前4位的复兴门、建国门、东单及雍和宫的综合节点重要度分别为0.913、0.662、0.357、0.259，变化幅度达0.654 5，有较强下降趋势；后11位车站综合重要度最大值为0.258，最小值为0.013，变化幅度为0.245，变化相对缓慢，总体上趋于稳定。沿着节点综合重要度的下降方向，节点承载压力呈现出较为规律的下降趋势，节点服务水平及节点加权介数的变化规律性较弱，即节点综合重要度值较高的车站其节点服务水平及节点加权介数值并未出现相同的变化趋势。总体来看，大部分车站的综合重要度与客流承载压力具有正相关性，小部分车站由于网络全局的便捷性与区域的枢纽作用使得其系统要度排序有所变化，如惠新西街南、国贸等虽然节点服务水平和节点加权介数较低，即它在全局的可达性与局部的连通能力较弱，但由于该区域经济发展吸引使其承担了较大的客流压力，因此，这些车站在网络中同样居于比较重要的地位；相反，如西直门、东直门、雍和宫等节点虽然承担的客流量较小，但由于在该车站衔接的线路数较多且在网络中位于几何中心位置，其节点服务水平和节点加权介数值较大，节点的综合重要度也比较大。这也进一步说明提出节点综合重要度的意义，即单个指标值并不能够全面体现出节点在网络全局的重要性，通过分析客流量与上述三个指标间的相关性，分析其内在联系，得到的综合重要度指标更具有实际意义，便于决策者进行综合决策。

4.3 节点重要度影响因素灵敏度分析

在节点综合重要度的计算中节点承载压力进一步反映了节点的连通性，具有其他两个节点不可替代的重要性，再此不做进一步分析。为探究节点服务水平、节点加权介数对综合重要度的影响，对上述两个指标进行单因素灵敏度分析，得到节点服务水平、节点加权介数对综合重要度影响的灵敏度分析，如图4所示。加权客流侧重于从节点内各换乘方向上的纽带作用和客流占比两个方面考虑，因而，排名靠前的主要为衔接线路数目较多且各换乘方向上衔接能力与客流量成正比的车站。同时，由于各换乘枢纽换乘站台的客流比重和衔接能力差异较大，使得节点加权介数变化范围较大。其次，综合重要度计算方法中节点加权介数的权重较高，因而综合重要度值对节点加权介数比服务水平更敏感；节点服务水平由该节点到达全网其他节点的方便程度(考虑到最短路径距离、中转换乘次数、列车服务频率)和各路径上客流比重两个方面计算得到，因此，排名靠前大多位于网络中的几何中心，且客流聚集度较高。

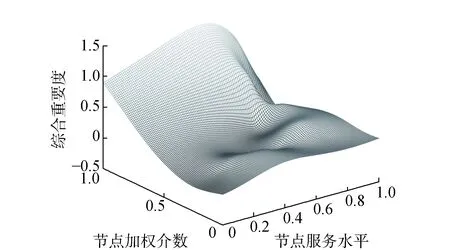
图4 节点服务水平、节点加权介数对综合重要度影响的灵敏度

5 结 论

城市轨道交通网络中关键节点的识别对初期线网建设规划具有重要指导作用，在综合考虑节点物理拓扑属性及客流属性的前提下，提出在客流加载条件下城市轨道交通网络节点重要度的相关评价指标，通过分析相关指标与客流量的相关性，得到节点综合重要度评价方法，进而对节点的重要度进行综合评估，以北京地铁网络进行实例分析，并得到以下结论：

1)节点承载压力与节点综合重要度之间呈现一定的正相关性，即沿着节点综合重要度的下降方向，节点承载压力呈现出较为规律的下降趋势。

2)节点服务水平、节点加权介数与节点综合重要度之间并无明显相关性，进一步说明单个指标具有不同侧重点，而综合指标更能从物理拓扑结构及客流属性方面体现节点的重要性。

3)节点综合重要度高的车站大多位于贯穿城区的干线和环线交汇的换乘站，以及对区域经济发展有较大影响的换乘站。

本文着重在宏观上识别客流网络中的重要站点，并未对站点重要度随全日时段不同的动态变化进行研究。同一车站分时段客流聚集现象差异巨大会使得站点各指标计算结果会发生显著变化，因此，将全日分时段来计算网络中车站节点的重要度动态变化是下一步的研究方向。