考虑乘客出行体验的需求响应式公交规划

于 展

(北京交通大学 交通运输学院，北京 100044)

在交通运输行业与“互联网+”交叉融合的背景下，符合共享经济发展趋势的需求响应式公交，利用互联网信息交互功能，为乘客量身定制出行方案。具体表现在预约和合乘两个方面。预约体现在用户通过移动端向运营方提交起讫点、乘车时间等相关信息。合乘体现在运营方面通过收集到的用户信息规划合乘站点和车辆行驶线路，合乘站点布设过多会导致车辆运行时间的增加，进而影响到乘车准时性的问题。合乘站点过少，则会导致资源浪费，无法体现预约公交公益性优势。因此，既要便利乘客出行，使乘客走行距离最小，又要充分考虑合乘站点数量与合乘路径的问题，合理的站点布设就显得尤其重要。在合乘站点布设方面蔡永旺[1]等对DBSCAN算法进行改进，实现对需求点的聚类；阮冠轩[2]等考虑乘客支付意愿,提出一种乘客出行中心点和孤立点乘客的确认方法，并基于重力模型求解；叶秋君[3]考虑固定站点站间距、服务区域宽度和乘客出行密度的影响因素，将站点的服务区域进行分割，以系统成本最低构建需求响应式公交站点选址模型；郭晓俊[4]根据地点决策、线路决策等实时定制公交系统关键要素分析，并结合北京天通苑社区的实际路网进行仿真模拟，证实模型定制流程可以在一定范围内提供服务水平较高的公共交通服务；胡列格[5]等人在确立了定制公交应有的合乘站点布局原则，并运用基于密度的孤立点检测方法，将一定区域内远离集中预约请求区域的“孤立点”进行剔除； 但结合需求响应式公交的运营情况，乘客步行距离及等候时间成本是影响乘客满意度的重要因素。因此需要将需求点抽象为具有软时间窗的需求点，并建立步行距离成本及等候时间成本的总成本模型，对公交站线进行规划。本文拟提出一种以乘客走行与等待成本最少为目标，以聚类为主要思想，对远离乘客密集区的相对孤立的乘客进行剔除，并基于DBSCAN、K-means进行合乘站点布设研究，并采用算例对其路径规划进行说明，为其投入实际运营建立系统化的方法。

1 模型构建

1.1 模型假设

1)需求点与合乘站点间的距离为二者的走行路线的平均距离;

2)需求点具有软时间窗区段，且等待时间具有成本;

3)对于每个需求点来说，仅由一个合乘站点提供服务;

4)对站点进行具体选址时，不考虑实际区域建设中该点是否适合设站。

1.2 需求点模拟

图1 带有模拟需求点的实验区域

2 合乘站点布设

2.1 剔除数据中的噪音点

为了向尽可能多的乘客提供服务，因此在站点布设过程中仅对远离乘客密集区的孤立乘客进行剔除，即去除“噪声点”。对于模拟需求点，为避免模拟点中的极端值影响，应先对模拟数据进行清洗，对于空间二维离散点，采用密度聚类的方法进行数据的先行筛选。在聚类数不可预知的情况下，可利用DEBSCAN算法进行一次聚类。该算法需要确定最小聚类数和最大扫描半径。考虑行人可接受最长行走距离将乘客所能接受的乘车最远步行距离平均值d作为筛选噪声点的主要依据。考虑需求响应式公交的开行要求，一个站点最少向两名乘客提供服务，当一个站点只服务两名乘客时，两个乘客间的最大距离为2d。

因此根据DBSCAN算法的性质，采取的聚类参数为Eps=2d，MinPts=4。根据问卷调研数据和相关参考文献，我们d值选定为800。筛选后结果及收剑速度如图2所示。

图2 筛选噪声点结果与收敛速度

考虑到随着城市交通发展，出行需求不断增加，一个站点服务的乘客过少势必造成资源的浪费。一辆小汽车最多同时能为4名乘客提供出行服务，为了承担更多客流。故在算例中将聚类参数调整为Eps=1 600，MinPts=4，再去除噪声点后，实验区域聚类效果如图3所示。随着聚类要求的提高，噪声点数量增加。DBSCAN的参数取决于数据中最稀疏的区域，其他较密较高的区域不受参数趋于严格的影响，因此DBSCAN算法对于剔除服务困难的乘客是十分有效的。

图3 优化参数后去除噪声点后聚类的结果

2.2 站点区域划分

对于去除噪声点后的数据集，由于预聚类采用密度聚类原理的DBSCAN算法，数据集中度较高，一般的聚类算法无法达到良好的聚类效果。针对该问题，采用基于距离聚类的K-means算法作为进一步聚类的核心指标，该算法将两点距离作为评价相似度的基本指标，可以将密集度较高的数据集进行进一步的簇类划分。K-means算法特点在于：同一聚类簇内的对象相似度较高，而不同聚类的簇内的对象相似度较小。应用过程中其难点在于初始K值的选取，文中采用K值从1开始逐步增加，直至达到乘客至合乘站点的步行距离满足要求。

K值不能无休止的增长，其最大值为簇类乘客数量，当K值等于乘客数量时，意味着每一名乘客的步行距离为0，变成一种“车找人”的模式，这势必会导致停车过于频繁，这种模式适用于乘客密度较低的情形。对于乘客密度较高的区域，为降低过多停站对乘客出行体验和成本带来的影响，可以规定一个站点的最少服务人数pmin，因此K值上限K*为簇类乘客数/pmin。因此布设站点前应对簇类乘客密度高低进行区分。

一个簇类的乘客密度即该簇类单位面积所含有的乘客数，由于乘客的分布是随机的，不确定的，使用包裹簇类的最小凸多边形作为簇类面积将会使得乘客密度偏小，因此在计算乘客密度时，以包裹簇类的凹多边形作为该簇类的面积。某一实验区域聚类范围如图4所示。图4中内侧线表示凹多边形，外侧线表示凸多边形。

3.HBO组患者治疗前后肺通气功能及动脉血气分析的变化：经1个疗程治疗后，HBO组患者的肺通气功能明显提高，低氧血症明显改善，与治疗前比较差异有统计学意义(P<0.01)。见表3。

图4 需求点封闭区域面积对比

2.3 参数优化

对于大规模的数据处理，凭经验手动调整聚类参数K值是不现实的，因此需要采用算法对聚类参数K进行进一步优化计算。采用走行距离和最小为优化目标，采用启发式算法进行大规模求解，具体算法描述如下：

1) 按照密度聚类结果，将数据集进行预分类。

2) 对于低密度类，无需进行优化直接输出K值即为最优参数。

3) 对于高密度类对K赋值并计算各站点距离和Z。

4) 若得到Z值小于原有Z值，将新值覆盖原值。

5) 改变K值重复(2)～(4)步骤直至最大循环步长结束。

对于1区域，K=3满足要求，聚类结果及站点布设情况如图5所示。

图5 k=3时站点布设情况

由于K-means寻找质心的过程是启发式的，同一K值时，每次迭代得到的聚类结果都略有差别。因此再每次确定K值后，可进行多次迭代，以乘客平均距离尽可能小为收敛目标，寻找较优结果，若一定次数后仍无法满足条件则继续累加。

但是仍然希望对所有的乘客都提供服务，因此对于完成站点布设后依旧无法提供服务的乘客，若接受较大的步行距离，可以对其票价进行适当优惠，以达到吸引客流的目的。

3 线路规划3.1 具有软时间窗的多车队约束模型

将需求响应式公交的服务模式可抽象为每辆车从起点出发，依次经过各个具有软时间窗的需求点最终到达终点的最短路径规划问题。由于需求点的访问过程必须在规定的时间窗内访问，如早到，则等待至指定时间，并计算等待费用；如晚到，则拒绝服务。因此对该问题进行研究并得到良好的决策结果对于公交运营服务质量的提升有重要意义。在建立模型时的条件约束主要是乘客时间窗约束、车队容量约束。考虑到需求响应式公交的运营特性，文中采用综合成本包括运输成本、等待成本和固定使用成本作为目标函数。

在约束条件方面，算法实现过程中，在每一个站点均要考虑：

1)软时间窗(Time Windows)。 车辆在整个过程中需要遵守时间规则：当到达指定需求点时，如早到，则等待至指定时间，并计算等待费用；超出时间范围则提前通过客户端告知乘客，对乘客进行票价优惠等补偿。

2)车队(Fleet)。 Fleet 由Vehicles 组成，且对其设置最大数量限制。

Fleet 的起终点均在发车中心Depot。车队的装载能力统一为Capacity。装载量在任何时刻不得超过装载能力。

一般认为Fleet 的服务范围为全路网，运行速度v=60 km/h。

实际应用过程中，可通过移动端收集乘客的起讫点及到达起讫点的时间窗数据，针对同一个时间窗内的起讫点布设合乘站点。站点布设完毕后，每个站点将具有服务人数、服务时间窗两个属性，即可建立数学模型进行求解。

3.2 模型建立

假设模拟实验区域内有一个站场中心，n个乘客上车点和对应的m个下车点，对每个乘客，要求将其从上车点送至下车点，所有站点的集合为V。车辆从站场中心出发并最后返回中心，且在本文中车库(站场中心)集合K中只有一个元素时，即单车型。每辆车的装载能力已知，每时刻每辆车承载人数不得大于满载人数。到达公交站的时间需满足相应的时间范围约束。期望综合各种因素使得综合成本(包括运输成本、等待成本、固定使用成本)最低。

公交车从站场中心出发，服务完乘客后仍需返回站场中心。每次载客人数应满足限制要求。车辆到达公交站点的时间必须在乘客要求的最晚时间前到达(含)，同时，先于客户要求的最早到达时间则有等待成本，路上时间为运输成本。

从站场中心出发要满足各个点的乘客出行预期需求，同时还要满足车辆自身的承载能力与用户点的软时间窗约束，具体的成本包括运输成本、等待成本和固定使用成本之和作为目标函数。因此，本例中决策变量为每辆车经过各站点的顺序以及到达、出发的时刻。目标函数变量声明如表1所示。

表1 目标函数变量声明

(1)

(2)

(3)

(4)

(5)

(6)

(7)

计算得出各合乘站点的信息汇总如表1所示。算例中共500个模拟需求点，且规划出站点共60个，其中上车点30个下车点30个，车辆满载为30人。各合乘站点的位置图如图6所示。

将60个规划站点信息输出即可得到表2。

最终可为车队形成完整的调度及运行方案，得到的车辆路径信息见表3。

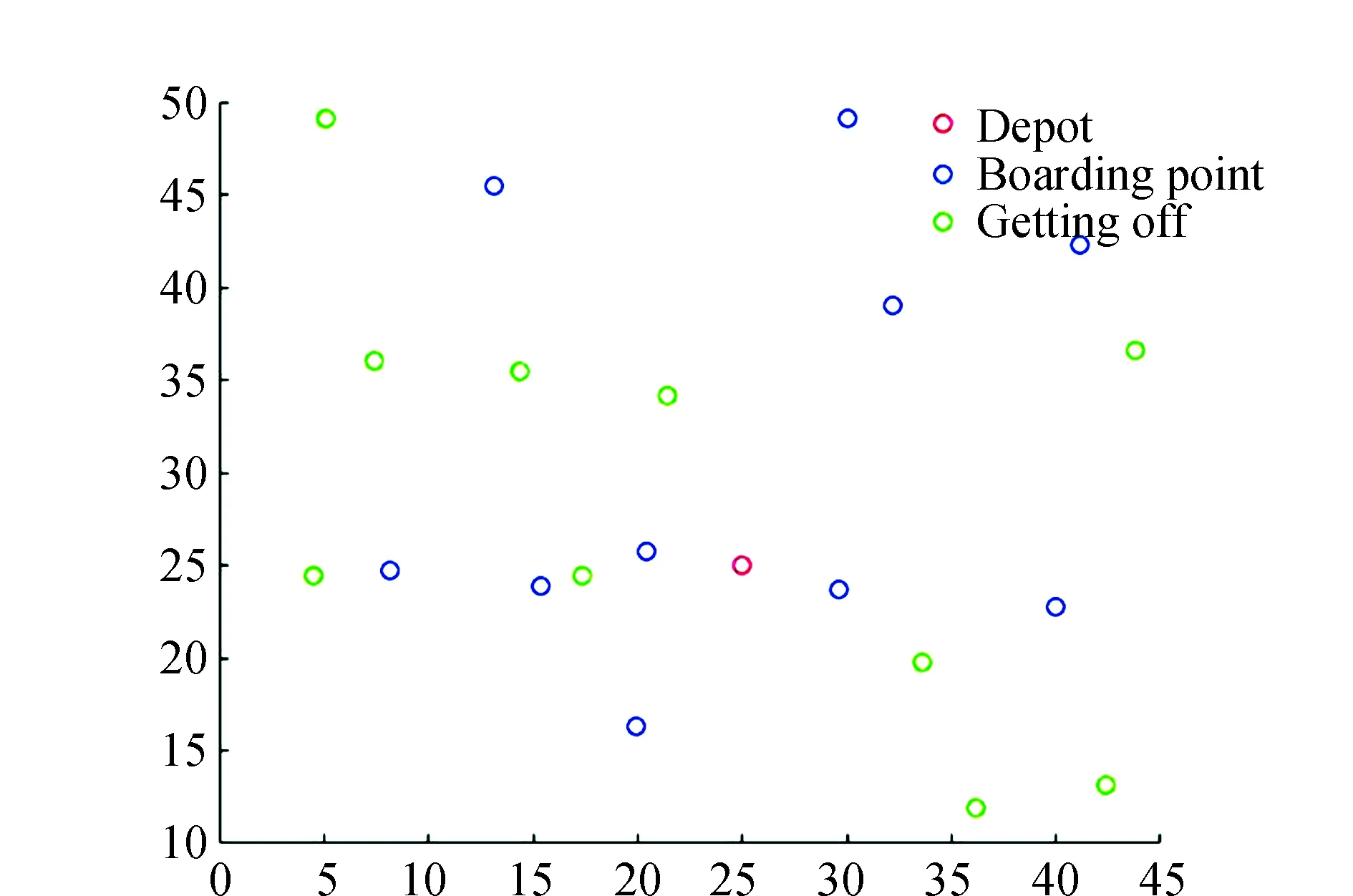
图6 合乘站点位置示意图

表2 各合乘站点信息汇总

表3 车辆顺序经过模拟点的序号

本例仅对单车型进行了计算，该模型也可以调整车队容量约束，将模型拓展应用于多车型车辆联运的调度方案。

4 结 论

本文充分考虑了行人走行距离，通过对具有软时间窗的需求点数据进行二次聚类，采用密度聚类算法进行预聚类，将清洗后的精细化数据进行按距离聚类，并将数据集进行分类，采用启发式算法对参数进行优化。对于聚类结果，基于行人走行距离和最短作为约束条件对站点选址进行分析。

对于规划好的站点选址建立具有软时间窗的多车队规划模型，并对模型进行求解，最终可以得到优化后车辆走行方案。可以有效地减少行人的步行距离及候车时间，对优化乘客乘车体验，提高车辆上座率，节约公交企业的经营成本具有重要意义。