高动应力水平下软粘土动力特性研究及应用
2020-04-21王元战李世纪雷继超
王元战,李世纪,雷继超
(天津大学 水利工程仿真与安全国家重点实验室 高新船舶与深海开发装备协同创新中心,天津 300072)
近年来,我国大量港口海岸工程结构建造在软土地基上。在波浪等动力荷载作用下,软土强度会发生明显变化。作用于结构的循环荷载会使软土地基不同位置产生大小不同的循环动应力,土体在不同水平动应力下其动力特性有较大差异。当地基土体受低水平动应力荷载作用时,土体的累积孔压和累积变形在一定循环次数后会达到稳定状态,土体发生一定程度的强度弱化现象;当地基土体受高水平动应力荷载作用时,土体累积变形和累积孔压快速发展,在一定循环次数后土体变形急剧增加,土体发生强度破坏。高、低动应力水平的临界值称之为临界动应力。Larew和Leonards[1]最早提出临界循环应力比的概念;Sangrey等[2]研究在不同应力水平下饱和粘土的循环动力特性,发现不同应力水平下土体具有截然不同的循环动力特性,在低动应力水平荷载作用下土体一直处于循环稳定状态,在高动应力水平荷载作用下土体会发生循环破坏。
目前,对低水平动应力作用下土体强度循环弱化问题,已开展大量研究工作。闫澍旺[3-4]得到了软粘土的抗剪强度弱化率随动应力、静偏应力变化的关系曲线;Soroush和Soltani-Jigheh[5]利用动三轴试验对混合土循环后剪切强度进行了研究,发现随着粒状颗粒的增加,土体会表现出类似超固结土的性质;Kaya和Erken[6]对Adapazari软土进行了研究,发现软土的循环后剪切强度随着塑性指数的增大而减小;王元战等[7-8]研究得到了考虑不同因素影响下的土体强度弱化模型,并将模型应用于有限元计算当中;Wang等[9]通过动三轴试验对海洋土进行了研究,发现软土循环后剪切强度随着不排水静偏应力、循环动应力和循环次数的增大而减小。
针对高动应力水平下的动强度研究,Ansal & Eren等[10]通过循环单剪试验对软粘土进行研究,认为软粘土的动强度与logN(N为循环次数)之间成线性关系;Tan K等[11]通过一系列动三轴试验,指出在较小静偏应力条件下预压作用会使土体动强度提升;Hirao & Yasuhara[12]通过一系列动三轴试验对重塑软粘土进行研究,通过引入不排水静剪切强度,得到了动强度与动荷载循环次数N之间的幂函数变化关系式;唐益群等[13]发现原状软粘土在长期荷载作用下的动强度随着动荷载循环次数的增加而降低;陈颖平[14]通过对萧山原状土进行动三轴试验研究,得到了动强度随围压和循环次数的幂函数变化公式;王军[15]通过一系列动三轴试验,指出随着土体超固结比的增大,土体的动强度增加;蒋关鲁等[16]分析了红层泥岩在低围压条件下的动强度特性,即在循环次数较小时,动强度的下降幅度更大。
循环荷载作用会在地基土体中产生高、低不同的循环动应力。目前研究大多针对低水平动应力作用下土体强度循环弱化问题。针对高动应力水平下的动强度变化规律,相关学者对动强度随循环次数和围压的变化关系进行了研究,并建立起了动强度模型,但建立的模型中没有考虑静偏应力和超固结比等因素对动强度的影响。虽然也有少数学者研究了超固结比等单一变量对动强度发展规律的影响,得到了动强度随超固结比等单一变量的定性变化规律,但并没有学者综合考虑循环次数、围压、固结静偏应力和超固结比对动强度的影响并建立起综合考虑上述影响因素的动强度模型。高动应力水平下土体的强度变化特性及其对地基承载力的影响,以及综合考虑高、低动应力水平下不同土体强度特性的数值计算方法等,是有待进一步研究的问题。
本文针对烟台重塑饱和软粘土开展了一系列动三轴试验,以循环次数、围压、排水静偏应力和超固结比为影响因素,研究了高动应力水平下重塑饱和软粘土的动变形和动强度发展规律,建立了综合考虑循环次数、围压、排水静偏应力和超固结比的土体动强度模型。依据已有的低水平动应力下循环强度弱化模型和本文建立的高水平动应力下动强度模型,通过二次开发将其在ABAQUS软件中实现,建立了综合考虑不同动应力水平下土体强度循环弱化和循环破坏的有限元数值模型,并通过实例研究了土体强度循环破坏对地基承载力的影响。
1 动三轴试验

表1 土样物理力学指标Tab.1 The physical and mechanical indexes of soil
1.1 重塑土样

图1 动三轴试验系统Fig.1 Dynamic triaxial test system
本文试验土样采取烟台港淤泥质粉质重塑软粘土样,利用原状淤泥质粉质粘土的容重和含水率作为控制条件(见表1),根据SL237-1999土工试验规程,采用分层击实法制备重塑土样。具体流程为先将原状土样碾散,放置碾碎后将土粒过0.425 mm筛,将过筛土分五层在高为80 mm、直径39.1 mm的标准圆柱形击实仪内击实,利用真空饱和法制备得到饱和重塑软粘土试样。
1.2 试验仪器
如图1所示,饱和重塑软粘土动三轴试验仪器选用英国GDS动三轴试验系统,该仪器可靠性好、功能齐全,可以非常直观的控制、设置仪器的试验参数,以及对试验过程进行动态监测。
1.3 试验步骤
将饱和试样取出,在等向围压σc下固结24 h,后保持排水阀开启,继续对土样施加排水静偏应力σh进行偏压固结,待静应变和孔压稳定之后,关闭排水阀,向土样施加循环动应力σd,使土体在循环过程中破坏,试验过程如图2所示。
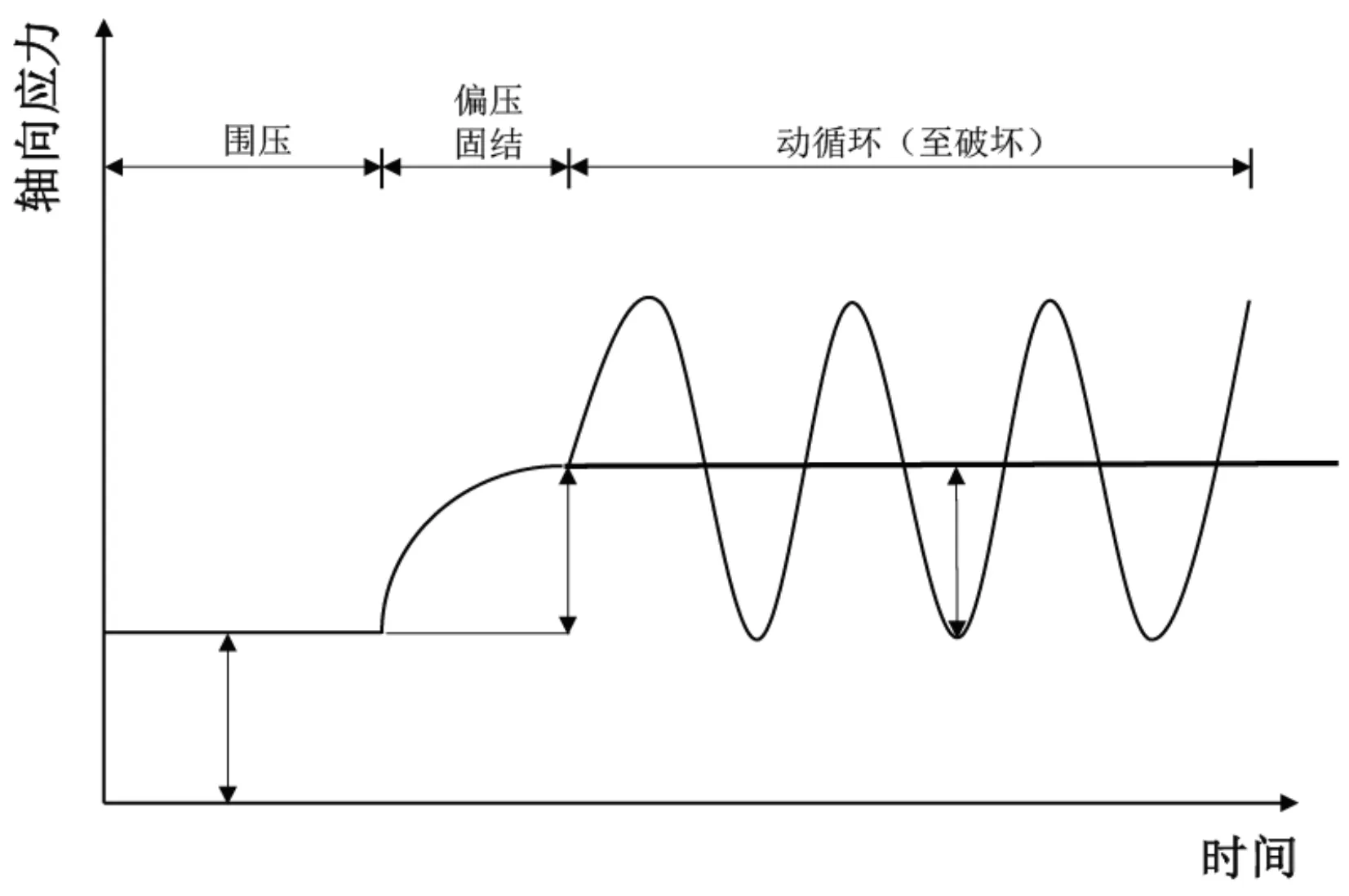
图2 加载过程图Fig.2 Loading process diagram
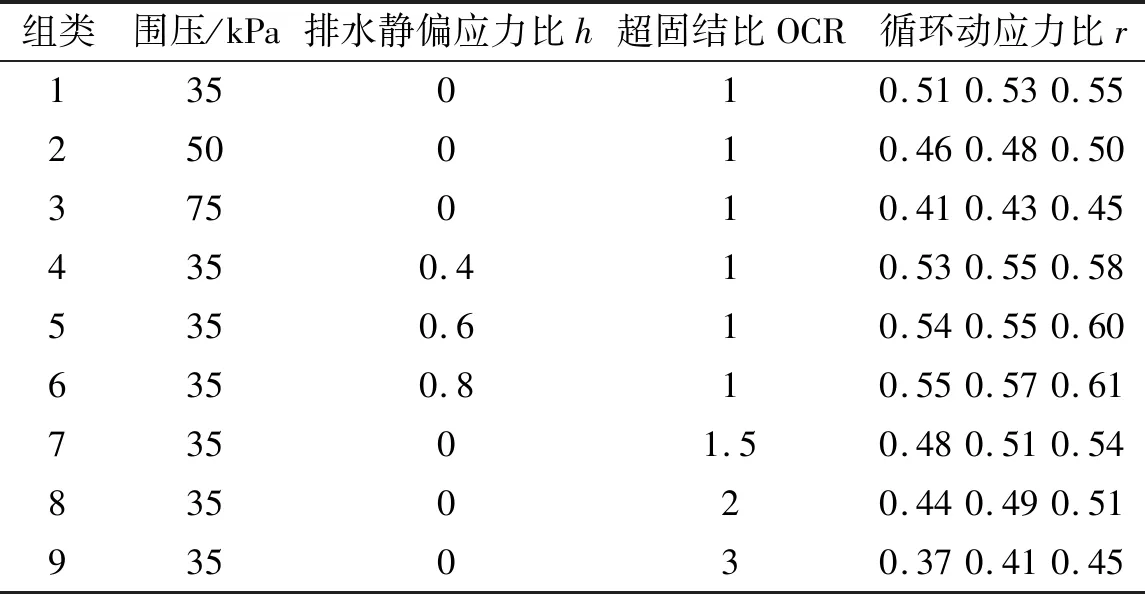
表2 动三轴试验方案Tab.2 Dynamic triaxial test scheme
1.4 试验方案
本文研究不同围压σc、排水静偏应力σh、超固结比OCR、循环动应力σd和循环次数对于软粘土循环特性的影响。OCR=Pc/P0为超固结比,Pc、P0分别为先期固结压力和现有固结压力;定义h=σh/σc为排水静偏应力比;r=σd/σc为循环动应力比。动三轴试验方案如表2所示。
2 试验结果及动强度模型
软粘土在动应力作用过程中存在临界动应力,当作用于土体上的动应力大于临界动应力时,塑性变形将出现显著增长并快速发展到破坏,当土体动应力小于临界动应力时,土体塑性变形随着加载次数的增加而趋于稳定。本文利用动三轴试验得到的不同围压固结条件下的动变形发展规律来对土体的临界动应力进行研究,动变形发展规律如图3所示。
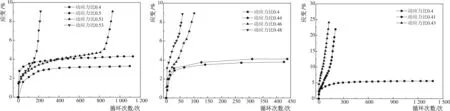

3-a35kPa围压下动变形发展曲线3-b50kPa围压下动变形发展曲线3-c75kPa围压下动变形发展曲线图3 不同固结围压条件下动变形发展曲线Fig.3Dynamicdeformationdevelopmentcurveunderdifferentconfiningpressureconditions
从图3可以看出,重塑软粘土在不同固结围压条件下的临界动应力不一样。在相同围压固结条件下的土体存在一个动应力比,当作用在土体上的循环动应力大于此动应力比时,在较短时间内土体动变形达到较大值,发生破坏;当土体的循环动应力比小于此动应力比时,土体动变形发展会随着循环次数的增大而逐渐趋于稳定,此动应力比称为临界动应力比。
根据试验得到的规律,在35 kPa围压固结条件下的土体,随着循环动应力比的增大,土体的动变形发展由一定循环次数后的循环稳定状态转变为在较短时间内动变形快速发展的形态,由试验结果可知,当循环动应力比小于0.5时,土体在一定循环次数后动变形保持稳定,当循环动应力比大于0.5时,土体在较短循环次数内达到较大变形,土体破坏,此时可以认为35 kPa围压固结条件下土体的临界动应力比为0.5。同理,利用相同的方法可以确定50 kPa和75 kPa围压下固结时的临界动应力比分别为0.45和0.4。可以发现,随着土体固结围压的增大,土体的临界动应力比不断减小。
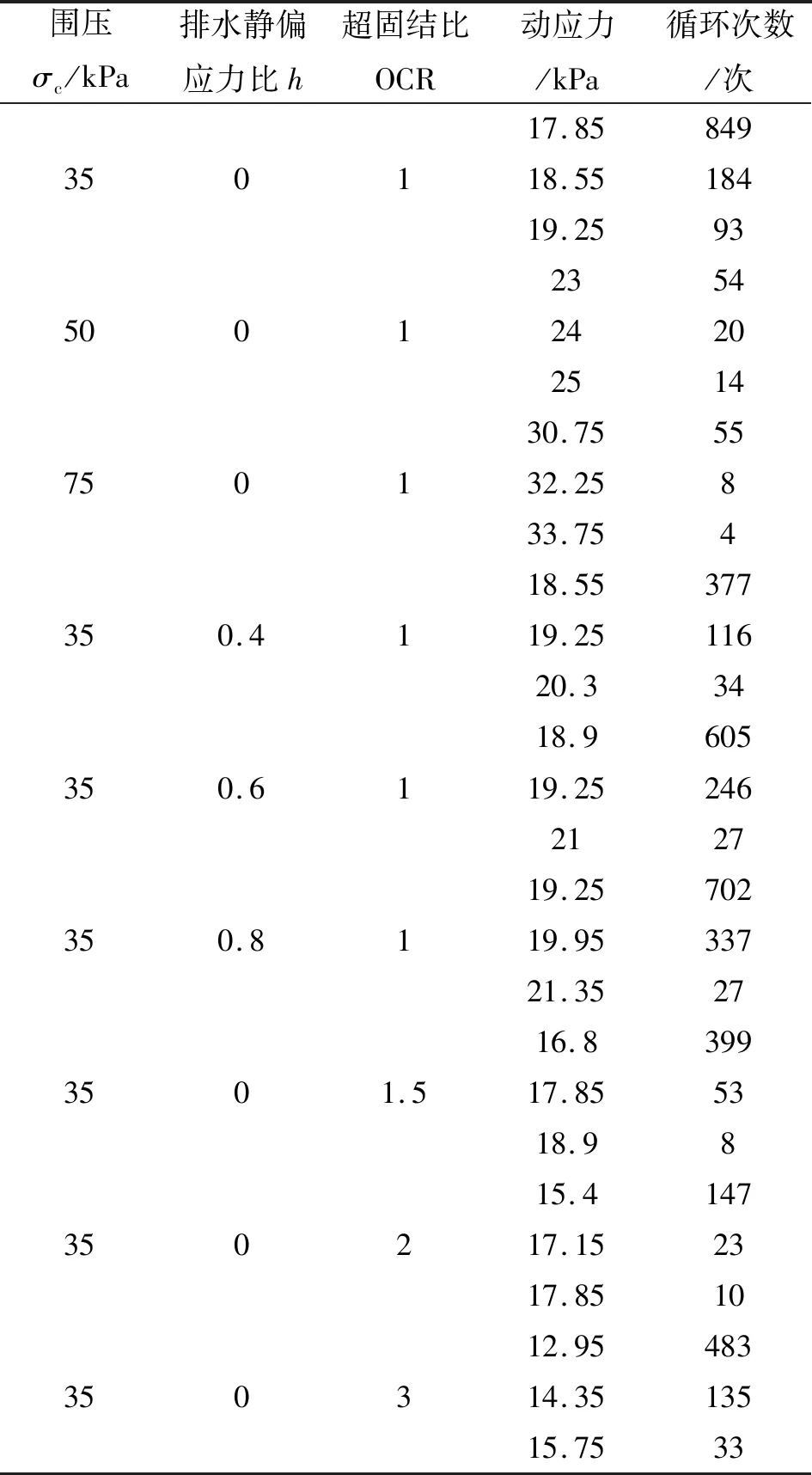
表3 5%应变破坏标准下的动强度数据Tab.3 Dynamic strength data under 5% strain failure criterion
本文针对Ansal & Eren模型进行一定的改进,建立考虑循环次数,围压,排水静偏应力和超固结比的动强度模型,如式(1)所示。
(1)
式中:σd为动应力;N为循环次数;σc、σj分别为围压、排水静偏应力;OCR为超固结比;a、b、c、d、e为相关拟合参数。
现取5%的累积轴向应变作为破坏标准,通过动三轴试验得到在此破坏标准下的动强度试验数据结果,利用动三轴试验数据拟合动强度模型相关参数,拟合数据如表3所示。
拟合结果如式(2)所示
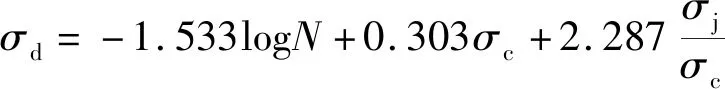
(2)
如图4结果所示,动强度在半对数坐标系下的发展规律近似地呈线性变化,动强度随着循环次数的增大而逐渐降低。由图4可知,将拟合出的动强度模型在半对数坐标系下展现,动强度模型对试验数据的拟合效果较好,R2=0.993。通过利用动强度模型可较好地预测土体动强度变化特性。
取5%的轴向累积应变作为破坏标准时,对不同围压条件下拟合的动强度直线拟合结果进行研究,可以发现不同围压下动强度的大小随着围压的增大而增大;同理,对于不同的排水静偏应力,可以发现动强度的大小随着试验静偏应力的增大而增大;在不同超固结比条件下,动强度大小随着超固结比的增大而减小。
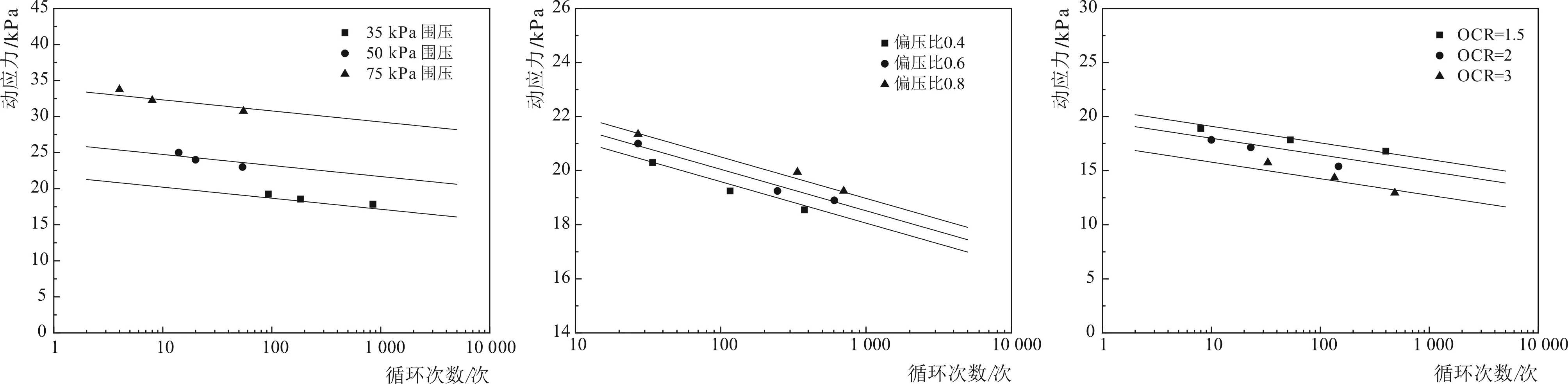

4-a不同围压条件下动强度直线拟合4-b不同偏压比条件下动强度直线4-c不同超固结比条件下动强度直线图4 5%破坏标准动强度直线拟合结果Fig.4Dynamicstrengthfittingresultunder5%strainfailurecriterion
3 有限元模型开发及验证
3.1 相关参数确定
为验证第3节建立的动强度变化模型的有效性,本节建立条形基础有限元模型来对不同工况下的地基极限承载能力进行分析,对比不同工况下数值模型的计算结果,探究偏压固结、循环弱化以及土体动强度变化规律等因素对地基极限承载力的影响。
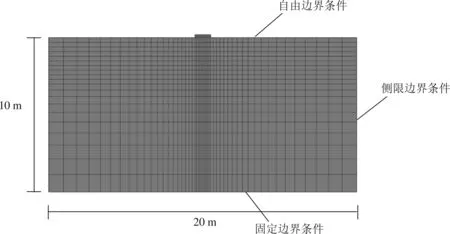
图5 土体边界条件图Fig.5 Soil boundary condition
条形基础有限元分析模型中土体采取摩尔-库伦本构模型进行计算,条形基础长取1 m,高取0.2 m,土体区域高为10 m,宽为20 m,土体边界如图5所示。土体的粘聚力c取30 kPa,内摩擦角φ取10°。在条形基础上施加应力控制的循环荷载,循环次数为300次,动力荷载幅值为20 kPa,荷载施加周期为8 s。
3.2 计算步骤
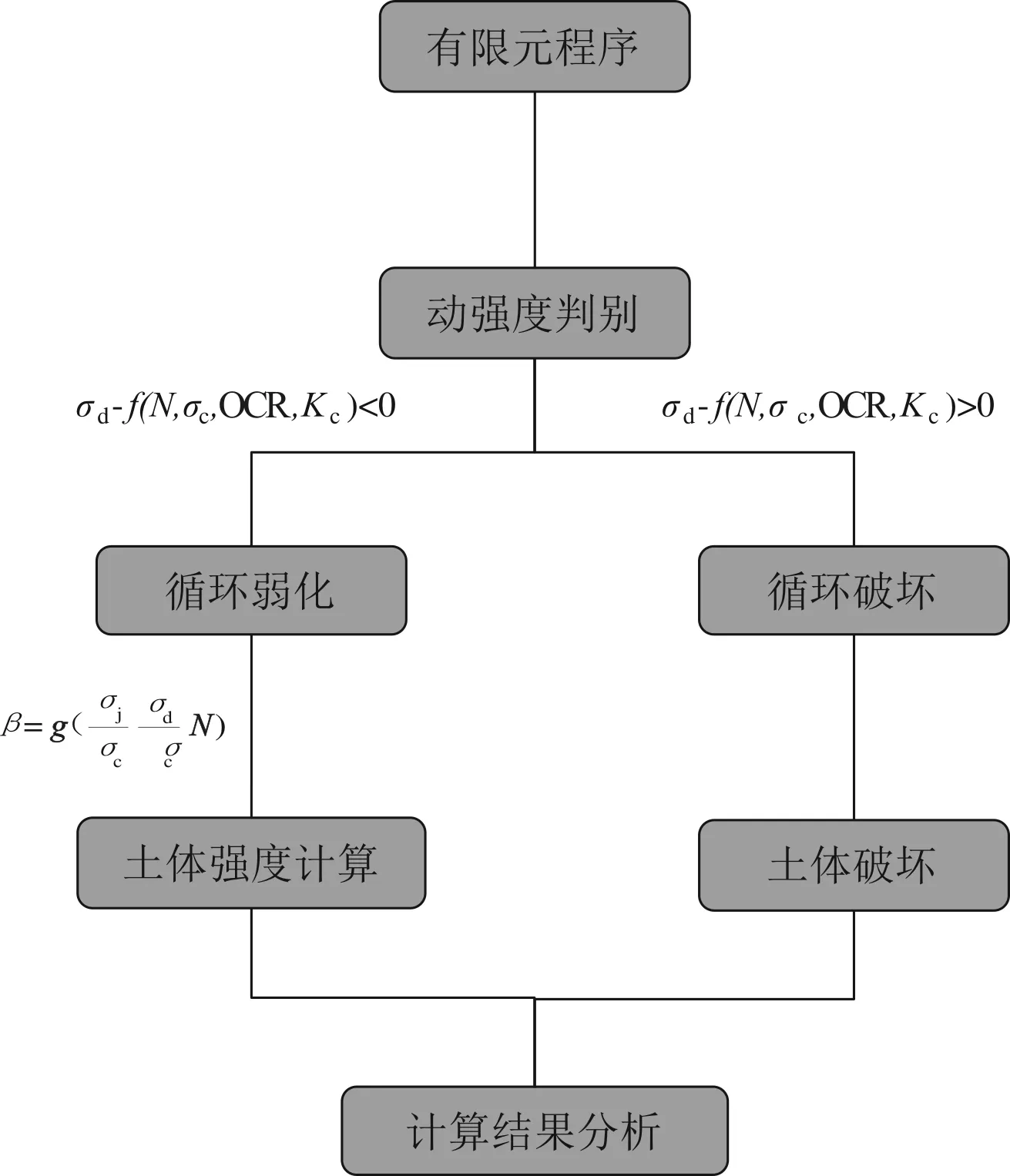
图6 数值计算流程图Fig.6 Numerical calculation flow chart
以往研究中已经得到了低动应力水平下的土体循环强度弱化模型,为了在有限元计算中对受到不同动应力幅值范围的土单元强度变化规律进行更为准确的数值模拟,需将动强度模型与弱化强度弱化模型进行结合。胡珅榕[17]利用弱化模型在ABAQUS中进行二次开发来实现了强度的不断变化,实现了强度指标c、φ的动态变化,如式(3)、(4)所示,其中循环强度变化系数γ是随着循环次数、围压、排水静偏应力、动应力变化的量。
φ′=arctan(γ(σc,σh,σj,σd,N)·tanφ)
(3)
c′=γ(σc,σh,σj,σd,N)·c
(4)
利用式(6)的动强度变化模型与胡珅榕的强度弱化模型进行结合,动力计算时在有限元程序中进行动强度判别,对不同应力水平下的地基土体强度进行计算,图6为模型计算流程图。
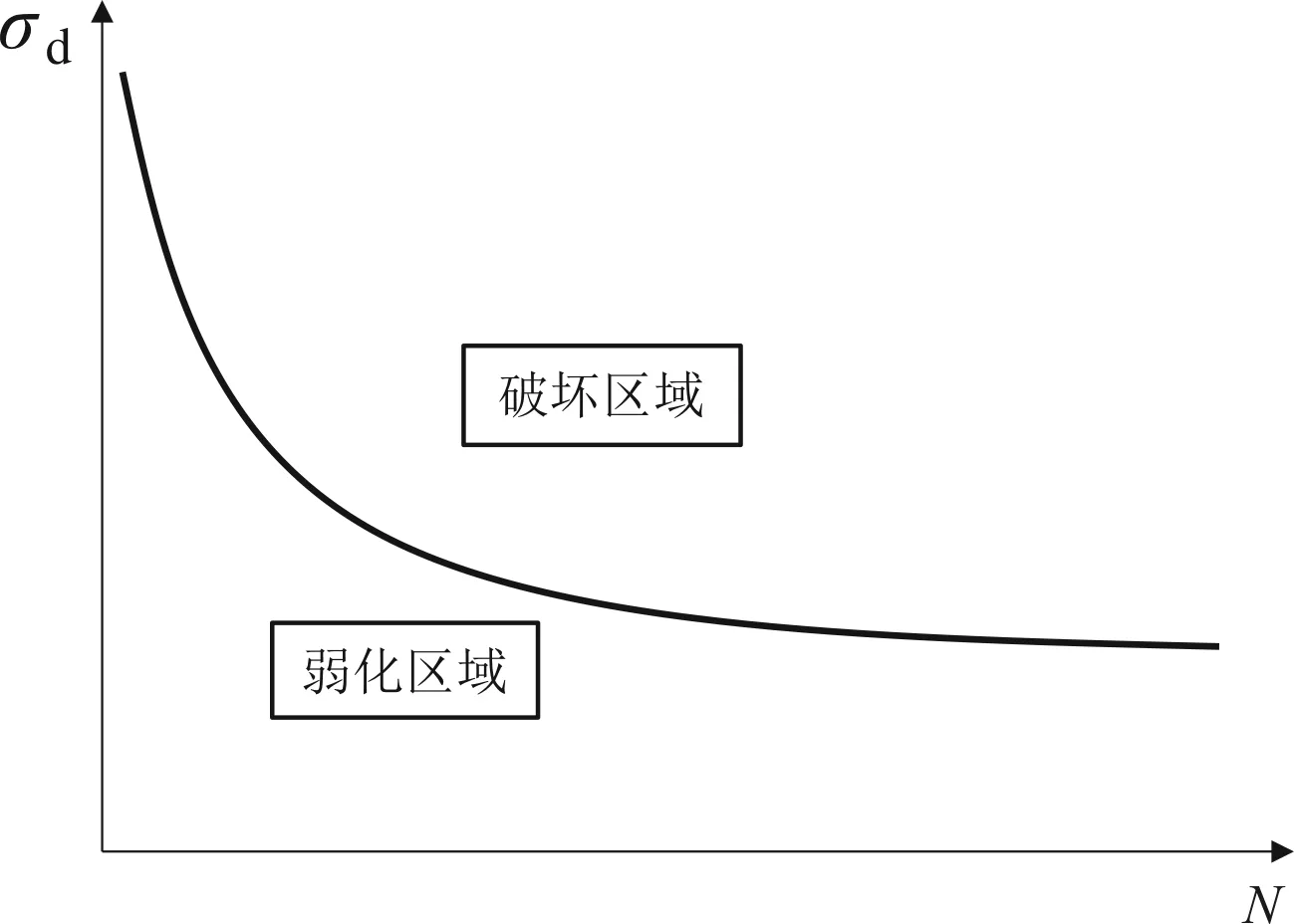
图7 土体破坏判定计算示意图Fig.7 The cyclic failure determination of the soil
如图7所示,图中曲线是动强度公式在线性坐标轴上的体现,动强度变化曲线将土体计算划分成破坏区域和弱化区域,在数值计算当中,模型通过子程序进行判定,当土体实时动应力小于动强度模型动应力时,可以认为土体处于循环弱化状态,土体利用弱化模型进行计算;当土体实时动应力大于动强度模型动应力时,认为土体在此时会迅速破坏,强度急剧衰减,定义土体强度并输出破坏区域。
3.3 条形基础模型验证
为验证条形基础有限元模型的合理性,本文采用普朗特尔地基承载力计算公式[18]对有限元模型计算得出的地基承载力结果进行验证。
普朗特尔基本公式形式为
pu=cNc+qNq
(5)
式中:
(6)
(7)
将数学模型计算得到地基极限承载力与普朗特尔理论解进行对比,结果如图8所示。
由图8可知,利用有限元模型计算得到地基极限承载力为279 kPa,普朗特尔理论地基极限承载力为250.5 kPa,模型计算结果与理论解误差为11.4%,两种解法误差较小且在允许范围内,说明建立的数值模型是可靠的。
3.4 动强度模型对地基承载能力影响
为探究动强度模型对地基极限承载能力的影响,本节利用上文建立的有限元模型对不同工况条件下的地基极限承载力进行计算,研究不同工况条件下地基极限承载能力的变化规律。
图9为条形基础的位移破坏图,在向条形基础施加幅值为20 kPa的循环荷载之后,再向条形基础施加逐步增大的竖向荷载使土体剪切破坏,条形基础边缘点下土体发生剪切破坏,且剪切破坏区域在地基中形成一片,成为连续滑动面,地基发生整体剪切破坏。


图8 有限元模型地基承载力结果与普朗特尔理论解对比Fig.8Comparisonoffoundationbearingcapacityresultsoffiniteelementmodelandprandtltheoreticalsolution图9 条形基础破坏图Fig.9Thefailureofstripfoundation
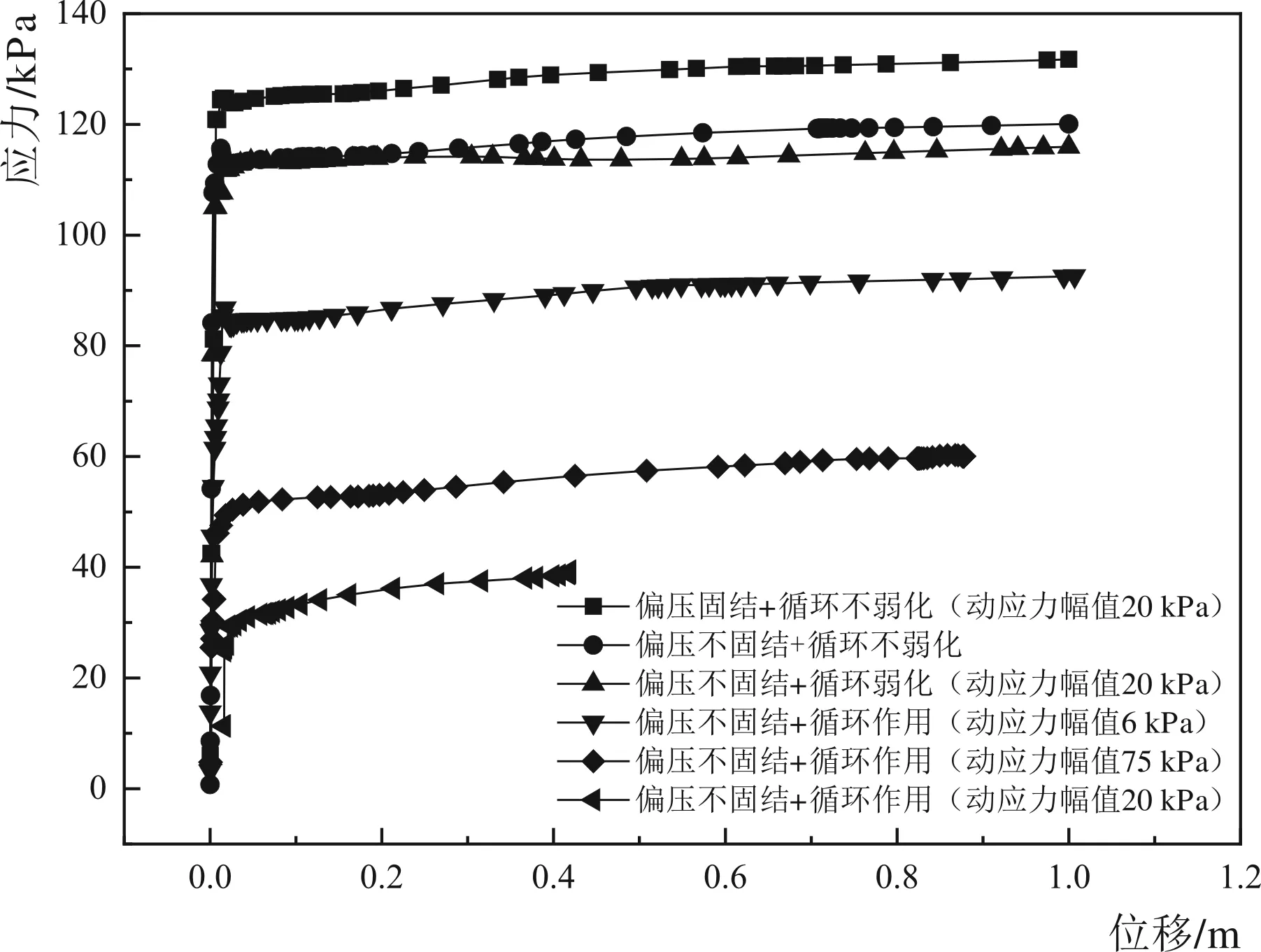
图10 不同工况下P-S曲线Fig.10 The P-S curve in different conditions
提取条形基础上某特征点的竖向位移,输出剪切破坏阶段的P-S(荷载-沉降)曲线,由于地基破坏属于整体剪切破坏,可以发现在不同工况条件下P-S曲线在沉降达到一定程度时曲线都会趋平。依据常用的地基失稳判别标准[19-20]本节取基于极限承载力的判别标准来对地基承载能力进行判别,即取P-S曲线趋于平稳,斜率为0时的竖向荷载作为地基的极限承载力。
图10为不同工况下的P-S曲线。采取20 kPa循环动应力幅值的偏压固结+循环不弱化,偏压不固结+循环不弱化,偏压不固结+循环弱化工况,以及循环动应力幅值分别为6 kPa、7.5 kPa和20 kPa的偏压固结+循环作用(考虑动强度变化规律)工况来研究其地基极限承载能力的变化规律;表4为不同工况下地基极限承载力及其相对偏压不固结+循环不弱化工况的地基极限承载能力的变化情况。

表4 不同工况下地基极限承载力及其变化率Tab.4 Ultimate bearing capacity and its rate of change in different conditions
由图10和表4可以得知,偏压固结作用对地基的承载能力有一定程度的提升,不考虑动强度变化规律的循环弱化会对地基承载能力造成一定程度的折减,在考虑动强度变化规律的循环作用下的地基承载能力相对偏压不固结+循环不弱化工况有大幅度折减,且随着加载于结构的循环动应力的增大,地基承载能力的折减程度有显著的提高。产生这种现象的原因是在较大动荷载作用下的地基土体发生破坏,土体强度急剧退化,对整体地基承载能力造成较大影响。
4 结论
本文通过动三轴试验和数值模型分析计算,得到的主要结论如下:
(1)在不同围压、排水静偏应力和超固结比条件下,土体动变形均随着循环次数的增大而增大,且高动应力水平荷载作用下的土体动变形存在拐点,在此拐点之前动变形稳定发展,在此拐点之后动变形迅速增长,土体在短时间内发生破坏。随着土体循环动应力比的不断增大,动变形增长越来越趋近线性变化,拐点变得不明显。
(2)临界动应力的变化规律:饱和重塑软粘土存在临界动应力,土体在35~75 kPa围压固结条件时,土体临界动应力是线性变化的,在此围压范围内临界动应力随着围压的增大而不断增大。
(3)建立了综合考虑围压、排水静偏应力和超固结比的土体动强度变化模型,分析了动强度的变化规律,可知土体动强度随着循环次数的增大而减小,随着围压和排水静偏应力的增大而增大,随着超固结比的增大而减小。
(4)将动强度模型应用于ABAQUS有限元计算当中,可知偏压固结作用可以提升地基承载能力,循环弱化对地基承载能力有一定程度削弱,若土体受循环荷载作用时考虑动强度变化规律,则地基承载能力会在循环弱化的基础上有进一步的折减,且随着循环动应力的增大,地基极限承载能力折减程度有显著提高。其原因是高动应力水平荷载作用下土体发生破坏,对整体地基承载能力造成一定影响。
