基于PSO 优化BP 神经网络的科技园区电力负荷预测
2020-04-21焦丰顺鲍重廷张瑞锋高洪洋
韦 波,焦丰顺,鲍重廷,周 浩,张瑞锋,高洪洋
(1.深圳供电局有限公司,广东 深圳 5180015;2.清华大学深圳国际研究生院材料与器件检测中心,广东 深圳 518055)
0 引 言
深圳供电局在深圳湾科技生态园已建成的智能电网项目(B-TEC),是2014—2016 中美智能电网合作期间的4 个示范项目之一,是南方电网在智能配电网领域的代表性项目。该项目建设了智能光伏微电网,制定了需求侧响应策略,开发了基于云平台的智能计量与高级用能系统,集成并检验了智能化的调度、配电、用电、分布式能源及可视化展示等核心技术。通过技术集成与商业模式创新,为电网提升客户服务能力进行了积极探索,提升了客户体验与价值。在未来亟需加强用户电力预测方面的研究,短期高精度电网电力预测是实现智能电网的关键,可带动“源-网-荷”智能化互联,为综合能源高效运行提供基础支撑,保障电网安全、可靠与高效运行。
电力系统中的电力数据的精准预测是主动配电网迈向智能化的重要步骤。短期电网预测是电网电力预测的重要分支。短期电网预测一般指对将来连续数小时到以天为单位的电网负荷数据进行预测,对电网调度电力的合理支配性[1-2]、发电机组的最佳出力组合、节点潮流最优而言极为重要,尤其是对未来智能化配电网及其电力经济性具有重要意义[3-5]。电网电力的预测精度的提升,还有利于减缓发电设备投资建设,同时提高现有机组的设备利用率[6-7]。
短期电网电力预测的探索由来已久,清华大学、华北电力大学、上海交通大学、国家电网、深圳汽航院等单位和康重庆、夏清[8]、牛东晓[9]、Chow Moyuen[10]、Willis H L[11]等许多电力方面的研究员,在理论和方法上做出大量的研究,有力地促进了电力预测精度的提升。在电力数据的预测过程中,大量的随机因素不断影响预测的精度,部分传统的神经网络因其拟合非线性的局限性,无法进一步提高预测精度,因此亟需不同技术理论之间的相互融合发展,以推动电力电网的短期预测水平的发展。本文中楼宇的短期电网电力数据特点有工作日和节假日电力规律各自的周期性,其中包括不同种类日内相同时段变化规律的相同性和近几年法定节假日负荷数据规律的相似性。
针对电网电力负荷的短期数据预测,方法有同类型相似日预测、周期性时间序列法以及气象因素的预测方法等。其中,BP 神经网络因在拟合非线性函数问题上的优势,在许多预测场景中被高频使用,但其在训练过程中易陷入局部最优,存在训练难以快速收敛等缺点[12-13]。经研究得知,遗传进化算法优化后的BP神经网络精度高于未优化的BP 神经网络,但仍存在局部寻优能力不足,易快速收敛、迭代速度慢等缺陷[14]。因此,本文提出PSO-BP 预测模型,避免了权值和阈值参数易陷入局部最优的困境,具有较强的泛化能力。最后,通过对深圳湾科技生态园的楼层负荷进行预测,分析优化后与未优化的各类指标,证明了本文所建立的短期预测模型的有效性。
1 粒子群优化BP 神经网络模型设计
1.1 神经网络结构设计
BP 神经网络的通用思想是梯度下降法,关键因素是信息沿着拓扑正向传递,并反馈计算结果误差。在信息传递过程中,参数信息从输入通道经隐含层逐层处理到输出通道。如果输出的结果未能达到预期设定结果,需根据误差结果和反向传递调整网络权值和阈值参数,使得神经网络预测的结果和已知输出结果尽可能一致。本文为了弥补天气数据的不足,提高电网电力数据的预测精确度,把输入层设置了包含一天最高温度、最低温度、天气、星期几、是否节假日、每天时刻、预测点前的两个历史负荷值输入等8 个输入神经元。
隐含层节点数的选择导致神经网络的结构变化,也影响着预测精度的高低。在经验公式的指导下,反复测试,根据结果得知可能的最佳隐藏层神经元的数量,并设置为最终训练用隐含层结构。输出层是预测的电力负荷Pout,为一个节点。BP 神经网络的整体构造图如图1 所示。
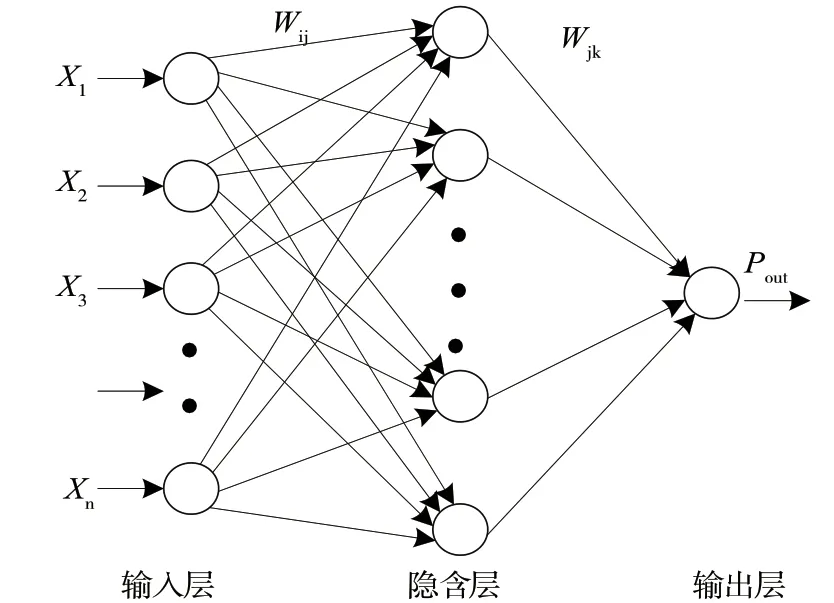
图1 BP 神经网络的拓扑结构
1.2 粒子群算法设计
BP 神经网络算法本身是非线性函数的“拟合器”,可将优化算法加入寻找最优目标值,否则算法很快会陷入局部最优值。
在一个D维的解空间内,有n个个体集合的解集X=(X1,X2,…,Xn),其中第i个个体代表一个D维的向量Xi=[xi1,xi2,…,xiD]T,表示第i个个体在D维解的区域的位置,也表示为该问题的一个可能优质解。根据目标适应度函数,可得出每个个体参数集Xi相对的个体函数值。第i个个体的速度为Vi=[Vi1,Vi2,…,ViD]T,其个体极值为Pi=[pi1,pi2,…,piD]T,个体集合的全部极值为Pg=[pg1,pg2,…,pgD]T。
在每一次迭代计算中,个体通过其最优值和全局最优更新自己的速度和位置,变换公式为:
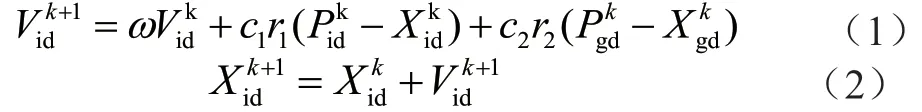
式中,w为权重因子;i=1,2,…,N;d=1,2,…,D;k为目前迭代计算的代数;Vid为个体的速度大小;c1和c2为非负定值数,也为加速度因子;r1和r2为出现在[0,1]中的随机数。为防止算法个体的盲目搜寻,可将位置的区域和速度大小限制在一定范围内;速度最大最小值[-Vmax,Vmax]及个体所在区域范围[-Xmax,Xmax]对个体移动计算作限定。
粒子的适应度即均方差为:
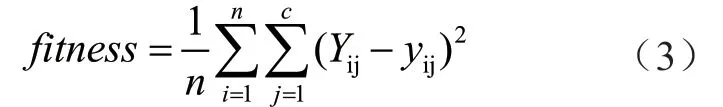
式中:n为训练集个数,c为结果输出个数;Yij是第i个训练样本的第j次训练的结果;Yij是第i个样本的第j次输出实际值。
采用粒子群进化算法对网络的权值和阈值迭代优化,计算过程如下:
①设置个体个数、位置边界[Xmin,Xmax]、个体移动速度的最大值和最小值[Vmin,Vmax]以及权重因子w、迭代终止条件和学习因子c1和c2,并对个体的位置xi与速度vi初始化;
辽东湾新区财政收支矛盾日趋突出,如何应对财政收支矛盾尖锐和资金压力日趋突出难题,成为摆在各级财政部门面前突出的问题。下面以盘锦辽东湾新区为例,简要分析近年来财政运行中存在的主要问题及困难,并从收入、支出以及财政预算管理等方面研究化解财政收支矛盾的对策思路。
②由输入数据集和输出数据集,利用式(3)算出每个个体适应度函数值,同时调整并记录粒子的极值pbest和群体极值Gbest;
③根据式(1)和式(2)对个体的速度和位置进行迭代更新;
④根据下式计算个体的速度和位置,不符合条件的按约束调整;
若Vi>Vmax,则Vi=Vmax;若Vi<Vmin,则Vi=Vmin;
若xi>Xmax,则xi=Xmax;若xi<Xmin,则xi=Xmin。
⑤重新计算粒子适应度值;
⑥是否达到结束要求,若目前迭代次数计算等于之前设定的停止条件,则结束迭代;否则,返回步骤①进行循环操作。
2 算例仿真
案例中,输入参数与BP 神经网络预测负荷相同,有8 个参数输入和1 个误差参数输出。该神经网络的构造为8-5-1,据神经网络计算法则得45 个权值和6 个阈值,因此算法设置的个体长度是51。粒子群参数设置为:学习因子1.49,迭代次数100,种群规模20,速度上下限和位置边界的绝对值为5。
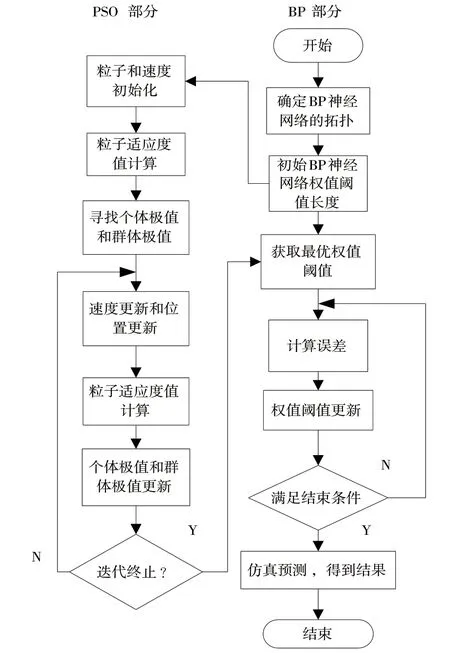
图2 算法流程
由图3~图7 可知,10 栋A 座8 楼上半年几乎没有负荷数据产生,下半年数据是典型的M 型写字楼工作日负荷曲线,与办公用电性质吻合、特点明显。因此,选取数据较为完整且有意义的下半年数据进行网络训练用以预测。选取深圳湾科技生态园10 栋A 座8 层7月1日至12月27日负荷及天气得到4 320 组输入输出数据。前4 296 组数据将作为训练数据,用于网络训练;剩余24 组作为测试数据,即预测27日负荷。把训练数据的均方差作为个体适应度值,个体适应度值越小,该个体越优。此外,7月1日至12月31日最高最低温度如图8 所示。
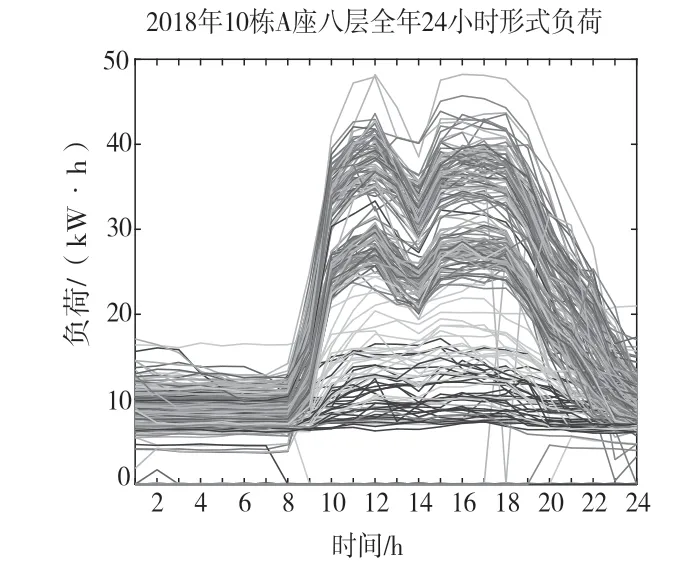
图3 2018年深圳湾10 栋 A 座 8 层负荷
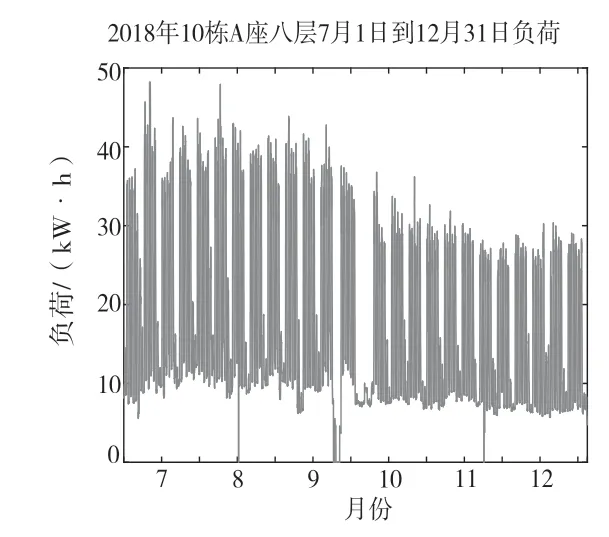
图4 2018年深圳湾10 栋A 座8 层半年负荷

图5 2018年1月1日至 6月30日负荷
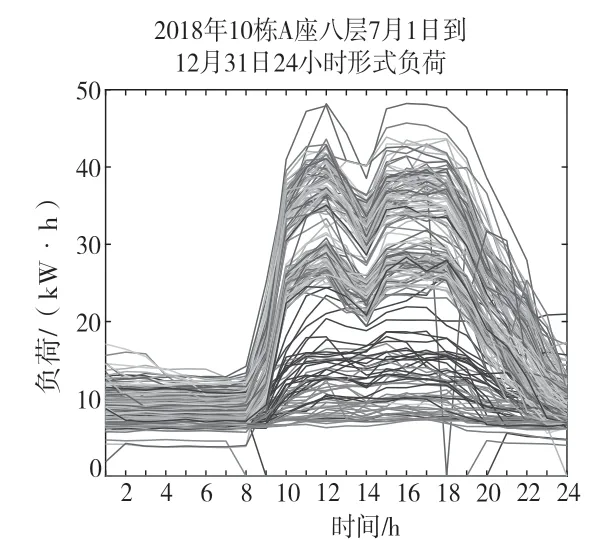
图6 2018年7月1日至 12月31日负荷

图7 7月1日至12月31日星期类型负荷

图8 7月1日至12月31日最高最低温度
从图9、图10 和表1 可以看出,经过PSO 优化过的BP 神经网络预测精度提高明显,具有重要的实际应用意义。
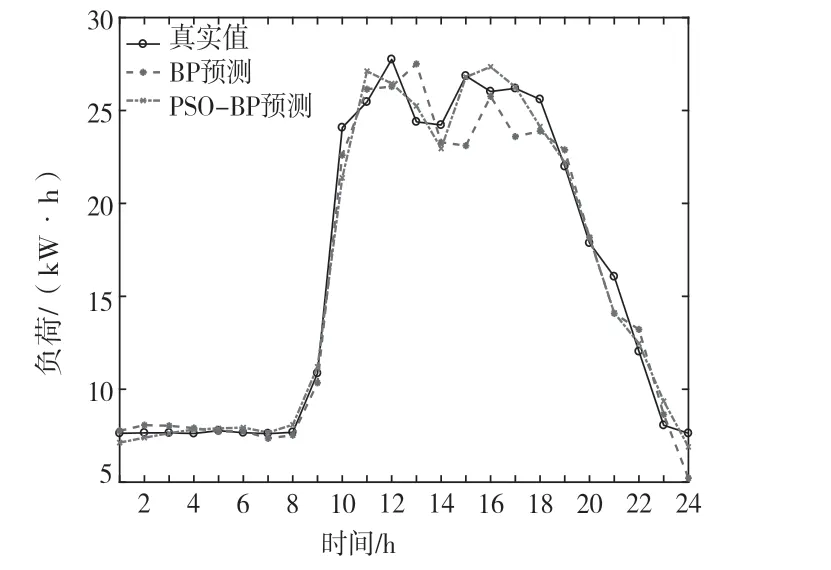
图9 PSO-BP 与BP 预测值对比
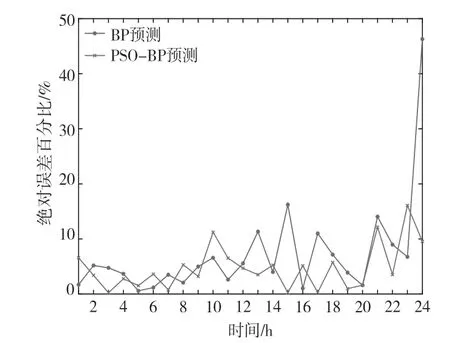
图10 PSO-BP 与BP 绝对误差百分比对比
为进一步验证预测算法的合理性和有效性,采用该算法分别预测连续工作日、星期五和星期六、星期日和星期一的两日负荷,预测结果如图11~图13 所示。
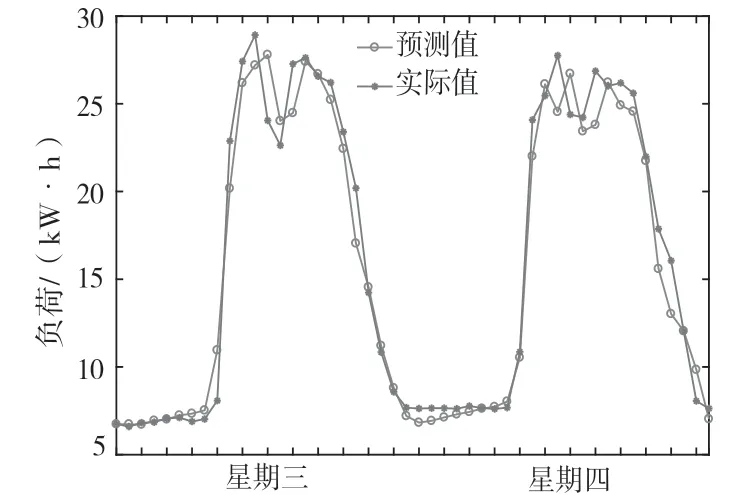
图11 预测连续工作日负荷
负荷预测值用于实际调度规划时,须考虑预测误差给调度带来的影响。本文提出的方法中需要考虑以预测值的±10%作为负荷波动的上下限考虑调度优化,如图14 所示。
3 结 论
通过采用PSO 算法优化BP 神经网络的初始权值与阈值,可以解决BP 神经网络初始权值和阈值确定的低效性、训练易早期陷入局部最优。建立的PSO-BP模型可以预测负荷趋势,可较为精确地预测居民用电,提高电网电力数据预测精度,具有较好的全局寻优能力,较为精确地预测了科技园区用户用电规律,具有一定的现实指导意义。后续工作可以通过改变进化代数、网络结构等方法,进一步提高电力负荷预测精度。

表1 两种方法预测指标
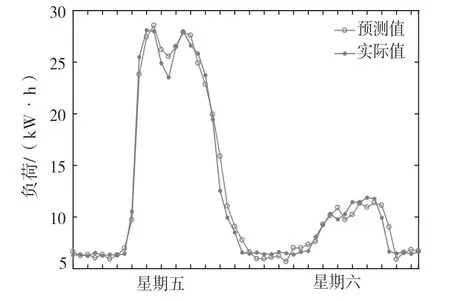
图12 预测星期五和星期六
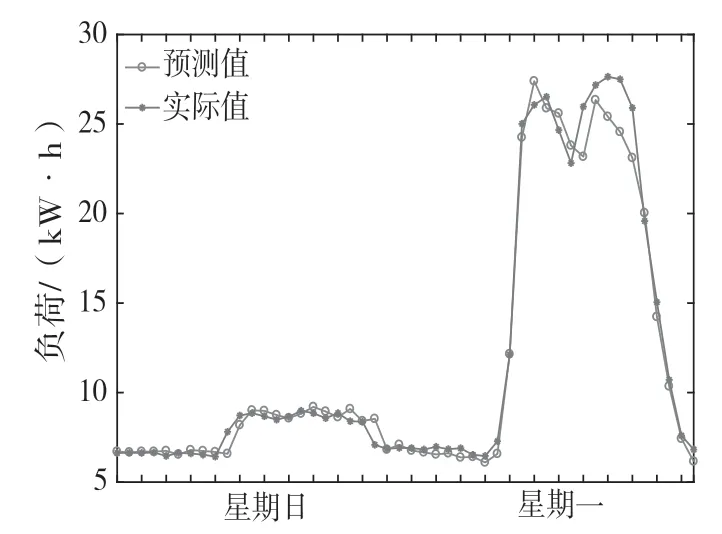
图13 预测12月23日和24日负荷

图14 预测负荷用于调度使用的误差带
