改进的粒子群算法在故障定位中的研究
2020-04-21段颖梨刘鹏华段小妹
段颖梨,刘鹏华,段小妹
(1.黑龙江科技大学 电气与控制工程学院,黑龙江 哈尔滨 150000;2.国网河南省电力公司直流管理处,河南 郑州 450000;3.国网汤阴供电公司,河南 汤阴 456150)
0 引 言
我国电网检测技术进展迅猛,传统的配电网定位划分为故障测距定位研究、直接定位算法和智能算法故障定位研究[1]。(1)测距定位研究。测距定位主要根据电源端所得的故障定位信息判定故障点和故障发生时间,有效降低了对工作人员的要求。(2)通过馈线自动化装置(Feeder Terminal Unit,FTU)上传的过流信息进行电网定位[2]。(3)基于智能方法的故障定位,在机器学习的基础上完善求解速度,用来提升定位的准确度。常用的人工智能算法包括遗传算法、模拟退火算法和粒子群算法[3]。
1 故障定位模型的建立
1.1 传统配电网故障区域定位模型
传统配电网中,故障定位不需要思量分布式电源,只需计及网络中主要的电源。传统配电网中故障定位编码只有0、1两种编码方式。配电网故障区间定位装置,如图1 所示。
1.2 含DG 配电网故障区域定位模型
1.2.1 故障电流的编码
由于接入DG 后电流方向会因为DG 的存在而发生改变,因此对开关编码方式重新定义,具体如下:(1)1,检测到正方向的故障电流;(2)-1,检测到负方向的故障电流;(3)0,未检测到故障电流。根据编码规则和故障点,可以判定出各个FTU 上传的故障过流信息。

图1 配电网故障区间定位装置

式中:Ij表示第j号支路处上传的电流信息。此处规定,送电端到受电端的方向为正方向。
1.2.2 开关函数
接入DG 后的配电网,当网络某支路短路时,经过开关的功率可能由多个DG 提供,故需建立新的开关函数:
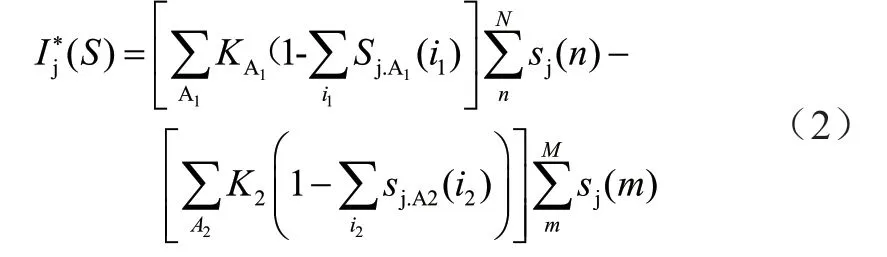
式中:第j号节点为分开点;KA1和KA2是对电源的关合因子,值为“1”表明电源连接电网,值为“0”表明电源未接入;Sj.A1与Sj.A2分别表示上半部分电源A1和下半部分电源A2到开关j 的路径中所经过线路的状况值;Sj(m)与Sj(n)分别表示j 号节点上、下半区的线路状况值;M、N表示上、下半区线路总数。
1.2.3 评判函数
评判函数值越低,表示关合电流与传递信息量的类似度越高。因此,建立评判函数如下:
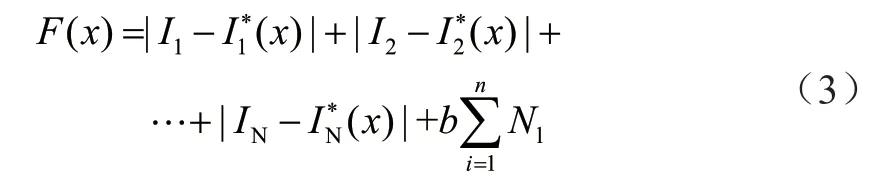
式中:IN为第N条支路FTU 传送的具体状况信息;为第N条支路的期望状况函数,即开关函数;N为节点总数;n为故障支路的数量;N1为故障支路数;b是修正系数,为防止误判而设定,b=0.5。
2 基于混沌理论和自适应改善的BPSO 算法故障定位
2.1 粒子群算法
粒子群(Particle Swarm Optimization,PSO)算法由Eberhart 和Kennedy 依据种群的进化捕食提出,传统粒子群的公式如下:

式中c1、c2为学习因子,表示各代粒子向最优值的学习因数,取值均为常数;rand()取值在[0,1]之间;ω为比重值;T是最大寻优次数;vid(t+1)和xid(t+1)表示t+1 次的速度和位置;vid(t)和xid(t)表明t次的速度和位置;t是目前优化次数;pid(t)是个体最优位置;pgd(t)是群体最优位置。
2.2 二进制粒子群(BPSO)算法
对于DG 的配电网故障定位,电流编码只有0、1和-1 三种编码方式,因而需要采纳离散的二进制粒子群算法求解[2]。对于粒子位置,取0 或1。粒子位置的取值取决于粒子速度的大小。对于定位问题,公式如下:

式中,rid(t+1)是在每次求解时生成的变化数,范围是[0,1]。sigmoid 是S 型。一般为了防止因变量越限过于平坦,设定速度范围[-4,4],公式如下:
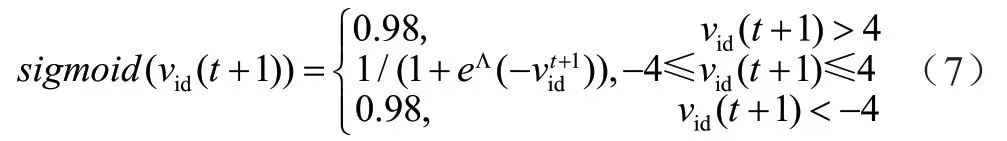
2.3 混沌理论
它具有不确定性、针对初始状态非常敏锐的特点[5]。混沌理论依照Logistic 理论,方程如下[6]:
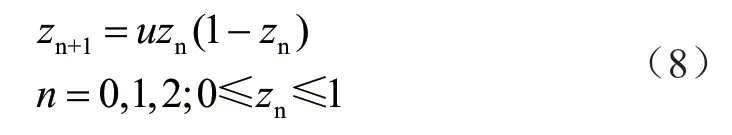
式中共进行n次变换,控制因子u取4 达到最优解。控制因子决定整体粒子的混沌情况。zn是变量,最优混沌群体如下:

ηj是变动的数,可以随机调整。根据式(10)进行自适应变换:
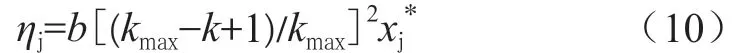
式中,b为邻边搜索半径,b=0.1。kmax是最终求解代数,k是目前代数,xj*是最优粒子。
2.4 混沌理论改进BPSO 算法
混沌数列可以改进BPSO 的初始值,从而解决了传统PSO 算法易于陷入小范围优化解的问题。同时,针对PSO 收敛时间长的问题,根据式(11)利用目标函数自适应改变权重变化:

f是当下目标值,fmax是目标均值,fmax是最大目标值。
改进算法流程如图2 所示。
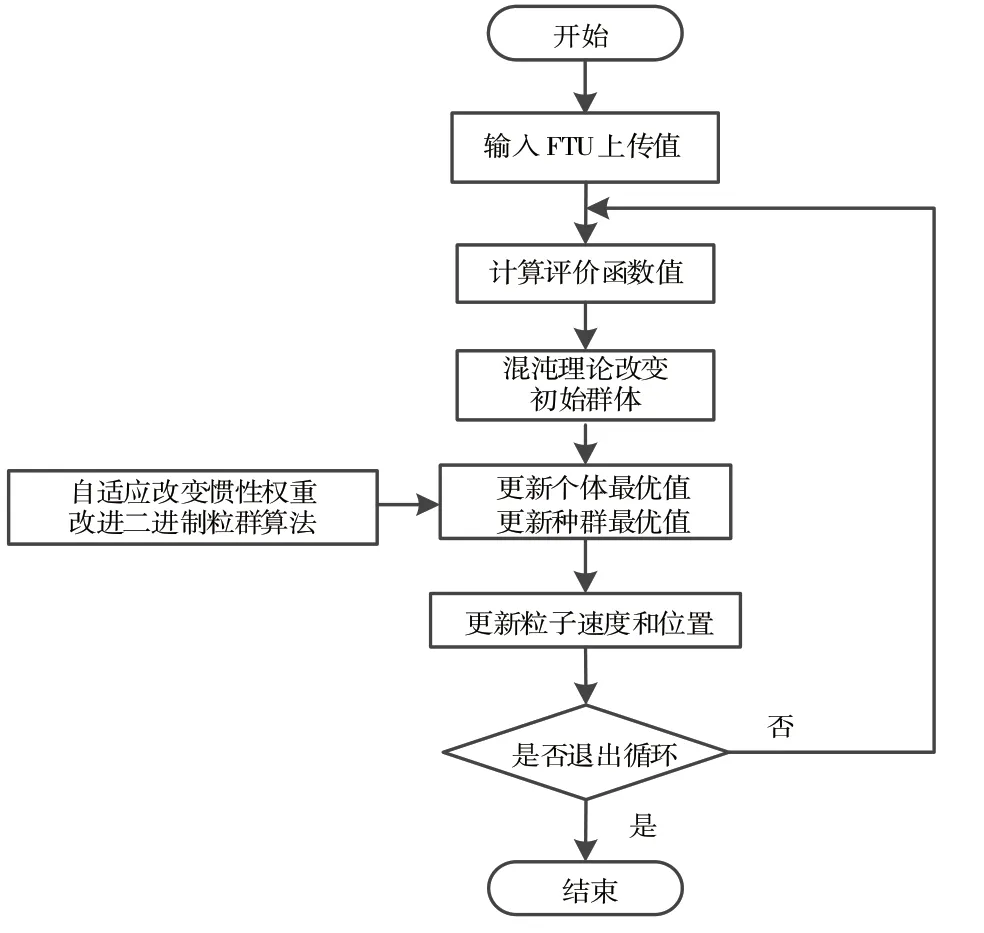
图2 改进BPSO 算法的故障定位流程图
3 算例分析
本文采用改进的IEEE33 节点配电网作为算例,在22 和33 节点加入DG,如图3 所示,在MATLAB R2018b 中进行仿真[6]。改进BPSO 算法参数设置如下:粒子群范围为20,最大迭代次数设为100,c1=c2=1.5,ωmax为 0.9,ωmin为 0.4,控制因子u取 4,搜索边界b=0.1。先由混沌理论找到最优群体范围,然后通过式(11)进行惯性权重的调整。
为验证文中所述模型和算法的优越性,本节利用标准粒子群算法和改进粒子群算法进行优化计算,同时采用几种典型的故障类型进行测试分析。
3.1 单点故障仿真
假设在不同线路发生单一故障,同时考虑不同的错误传递信息进行仿真分析,结果如表1 所示。
分析表1 的故障定位结果可以发现,在网络发生单点故障时,无论故障发生在什么位置和故障信息是否发生畸变,结论均正确。
3.2 多点故障仿真
假设线路发生多处故障,如表2 所示,分别进行BPSO 和改进 BPSO 求解。
从表2 分析可知,发生多处故障且信息变化时,改进算法仍能正确判定故障。
3.3 适应度曲线分析
如图4 和图5 所示,本文所采用混沌理论改进的BPSO 算法,在迭代次数、寻优时间方面更小,能够在短时间寻到故障,对应的最小适应度为1.6。
下面对两种方法下100 次内的寻优时间和准确率进行仿真分析,结果如表3 所示。

图3 包括DG 的33 节点配网图

表1 单点故障仿真结果

表2 多点故障仿真结果

表3 两种方法单点、多点故障定位仿真结果对比

图4 单点故障BPSO 和改进BPSO 算法的适应度曲线
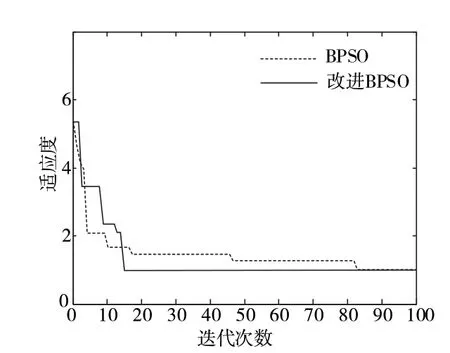
图5 多点故障BPSO 和改进BPSO 算法的适应度曲线
4 结 论
本文对BPSO 算法采用混沌理论改进,和普通BPSO 算法相比,混沌数列可以改进BPSO 的初始值,从而改变传统BPSO 算法易于陷入小范围优化解的情况。在MATLAB 中的仿真,证明了改进方法的有效性。
