一种高效的移动对象伴随模式挖掘算法

王齐童,王 鹏,赵郁亮,2,汪 卫

(1.复旦大学 计算机科学技术学院,上海 201203; 2.公安部第三研究所,上海 200031)

0 概述

卫星导航和无线通信等技术的广泛应用产生了大量位置信息数据,使得路径导航、社交网络地点推荐等基于位置的服务(Location Based Service,LBS)成为研究热点[1]。移动对象的轨迹相似性是时空数据挖掘的重要问题,对相似性的研究可以只考虑空间特征,如野生动物的迁徙轨迹分析、车辆轨迹分析,也可以同时考虑时间和空间2个维度的特征,如本文研究的移动对象伴随模式挖掘问题[2-3]。

移动对象的伴随模式挖掘是指找到在给定时间段内经常同时出现在某些地点的对象集合,该技术在智慧城市与城市安全、基于地理位置的用户行为分析中有广阔的应用场景:在城市道路监控摄像头捕捉到的车辆过路信息数据集中挖掘伴随车辆,有利于公安队伍寻找团伙犯罪的嫌疑车辆;在手机基站接入信息数据集中挖掘伴随人群,有利于移动运营商分析用户的时空特性,协助基站的规划与建设;在社交网络地点签到数据集中挖掘伴随用户,可以协助社交软件进行好友、兴趣点等多维度的推荐,也可以提供拼团服务。

在上述移动对象的伴随模式挖掘应用中,对象(车辆、人群、用户等)在时间维度上密集地连续分布,但在空间维度上则是离散分布(道路摄像头、手机基站、商铺等),这与传统的野生动物迁徙轨迹分析等轨迹相似性分析应用中对象时空信息由安装的GPS传感器定期传输,也即时间离散、空间连续的特点完全不同。此外,上述应用中数据量大且中间结果冗余度高,对此,传统方法是在每个离散的时刻进行空间聚类,再计算两个或多个对象被聚集到同一聚类中的次数,与给定阈值进行比较。而本文研究的移动对象伴随模式挖掘问题的数据量超过了传统方法能够处理的范围。以北京市道路监控摄像真实数据集为例,每天的捕捉到的不同车辆数约200万,车辆的相遇次数逾2亿,但其中超过99%的相遇都是冗余结果,这两个特点给移动对象的伴随模式挖掘带来了挑战。

本文面向时空数据相似性挖掘中时间连续、空间离散的新型应用场景，定义并形式化移动对象伴随模式挖掘问题。针对移动对象时间连续、空间离散的特点，设计基于单位步长滑动窗口的算法框架，并采用贪心选择策略[4]消除滑动窗口之间的重叠，利用Apriori性质[5]生成多个对象的伴随模式；针对移动对象时空局部性的特点，设计基于摘要信息的细粒度剪枝方法，并根据不同强度的时间和空间局部性提出4种摘要信息提取策略。本文将这两种剪枝策略层叠使用到算法的基本框架中，以提高对移动对象伴随模式挖掘问题的求解效率。

1 相关研究

大量学者针对移动对象轨迹相似性挖掘进行了研究,方向主要是空间维度的轨迹聚类[6]和时空2个维度的移动对象聚类[7-8]。

对于不同的移动对象时空聚类应用场景,先后有Flock[9-10]、Convoy[11]、Swarm[12-13]、Gathering[14-15]等问题被提出并研究。这四种移动对象聚类模式的基本算法框架均为在每个时间片上分别进行空间聚类,判断2个或多个对象是否满足定义的方法,是计算其位于同一聚类的时间片数量是否超过给定阈值,主要优化方法则是利用相邻时间片之间聚类的相似性。在基本框架上,Flock以距离半径来确定空间是否接近,并要求位于同一聚类中的时间片是相邻的。Convoy用基于密度的聚类方法来获得空间上的相似性,同样要求时间上的相邻性。Swarm定义相似模式可以在一定时间阈值内间隔性出现,聚类方法也是基于密度的聚类。Gathering定义相似模式的对象集合中的对象可以是动态变化的,例如在游行中会有人随时进入和离开。但上述4种问题定义均是在时间离散、空间连续的背景或假设下进行的,且对象的数量少,这与本文研究的应用场景中时间连续、空间离散、对象量大、中间结果冗余度高的特点是不一致的,直接使用除了会因为时间分割而带来漏解的问题,也会由于大量冗余中间结果严重影响性能。

在近期其他相关的工作中:文献[16]从子图搜索的角度研究了移动轨迹相似性的问题,但并未考虑轨迹的时间特性;文献[17]与本文研究的问题背景相似,采用了基于Apache Spark[18]的分布式计算流程,但未能解决大量冗余中间结果的问题。文献[19]采用了基于Apache MapReduce[20]框架设计的分布式Swarm挖掘算法,但同样未解决大量冗余中间结果的问题。文献[21]提出的Episode与本文的问题定义类似,但要求模式中的对象在时间上保持顺序。

2 问题定义

本文研究的移动对象伴随模式挖掘问题,针对的是在给定时间段内经常出现在同一地点的对象集合。为明确出现在同一地点的含义,首先定义相遇的概念,然后为精确计数对象集合出现在同一地点的次数定义最大有效相遇集合的概念,其大小即对象集合出现在同一地点的次数。将计数对象限制为有效相遇是为了消除对某对象某一次出现的重复计数。下面将分别对以上概念和移动对象伴随模式挖掘的问题加以形式化说明。

定义1(k-相遇) 给定时间长度阈值εt和记录集合R={r1,r2,…,rk},若∀r1,r2∈R,ri={oi,li,ti},rj={oj,lj,tj}满足oi≠oj、li=lj、|ti-tj|≤εt这3个条件时,称R为一次k-相遇,记为e。

不失一般性,在此假设∀r1,r2∈e,如果i≤j,则ti≤tj。因此∀r1,r2∈R,|ti-tj|≤εt等价于tk-t1≤εt。称t1为相遇e的开始时间,tk为相遇e的结束时间。

定义2(有效相遇集合) 给定时间长度阈值εt和对象集合O,满足以下2个条件的相遇集合E={e1,e2,…,ek}被称为对象集合O的有效相遇集合,也记为E(O):1)∀ei∈E,{oi,j|ri,j={oi,j,li,j,ti,j}∈ei}=O;2) ∀ei≠ej∈E,ti,1>tj,k∨tj,1>ti,k。

第2个条件要求在同一个集合中的相遇在时间上是不重叠的,称为非重叠性。一个对象集合O会有多种不同的有效相遇集合E(O),把最大的有效相遇集合记为EL(O),指O中对象相遇的最多次数。

定义3(伴随关系) 给定时间长度阈值εt和频率阈值εe,对象集合O满足伴随关系当且仅当|O|≥2且|EL(O)|≥εe。

将所有满足伴随关系的对象集合记为C,所有满足伴随关系的大小为k的伴随关系集合记为Ck。由于满足伴随关系的对象集合会具有冗余性(例如满足伴随关系的对象集合的非平凡子集都满足伴随关系),因此本文进一步给出闭合伴随关系的定义:

定义4(闭合伴随关系) 对象集合O满足闭合伴随关系当且仅当∀O′∈{Oi||EL(Oi)|=|EL(Oi)|},O∉O′。

对象集合O满足闭合伴随关系,即O的所有超集的最大有效相遇集合都小于O的最大有效相遇集合。移动对象的伴随模式挖掘问题是在给定数据集合中找出所有闭合伴随关系,移动对象伴随模式挖掘定义为:给定时间长度阈值εt和频率阈值εe,返回数据集RRec中所有满足闭合伴随关系的对象集合。下文以图1所示的记录为例对移动对象伴随模式挖掘问题和相关定义进行说明。

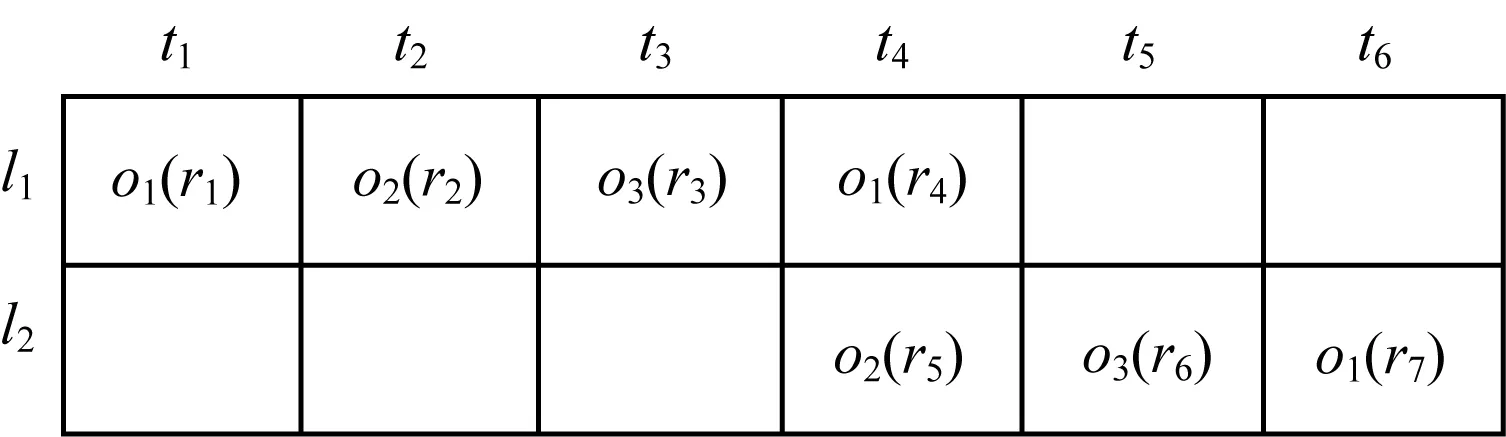
图1 记录样例Fig.1 Example of records

图1中的每一个元组代表了一条记录,l1行t1列的元组o1(r1)代表对象o1在t1时刻位于位置l1,也即记录r1,r1={o1,l1,t1}。不失通用性,本文假设时间等间隔分布,间隔长度为1,即∀i,j,|ti-tj|=|i-j|。给定长度阈值εt=4和频率阈值εe=2,在表1中分别给出定义1～定义4的样例。

表1 定义1～定义4样例Table1 Examples of definition 1 to definition 4

表1中的样例基于图1中的记录。在满足εt的[t1,t4]内,o1出现了2次,o2和o3各出现了1次,因此,有2个3-相遇(e4与e7)和5个2-相遇(e1、e2、e3、e4、e5、e6)。生成相遇之后,按照非重叠性的要求构造有效相遇集合,共得到19个有效相遇集合(包括11个大小为1的集合),并从中选择最大有效相遇集合。当候选的最大有效相遇集合不止一个时,任取一个即可以满足定义要求。所有的最大有效相遇集合均大于等于εe,因此,得到4个满足伴随关系的对象集合,其中C4为满足闭合伴随关系的对象集合。

表1的样例也体现了移动对象伴随模式挖掘问题的大量冗余的中间结果这一特点与挑战。在表1提供的样例中,虽然只有1个满足闭合伴随关系的对象集合,但需要检查11个相遇、19个有效相遇集合和4个满足伴随关系的对象集合,其中只有2个相遇、1个有效相遇集合与查询到的满足闭合伴随关系的对象集合相关。

3 基于滑动窗口的宽度优先搜索算法

本文设计基于滑动窗口的宽度优先搜索算法框架,采用Apriori 剪枝策略挑选候选对象集合、缩减搜索空间,利用贪心策略直接选择具有非重叠性的最大有效相遇集合。由于中间结果的冗余性是移动对象伴随模式挖掘的难点,因此额外设计针对2-相遇的剪枝过程。

本文算法设计的基本思路是首先生成满足伴随关系的大小为k的对象集合,再利用Apriori性质来选择大小为k+1的候选对象集合。在生成满足伴随关系的大小为k+1的对象集合时,分别检查每个地点按时间排序的每个记录rj,生成长度为[tj-εt,tj]的滑动窗口,窗口中每组(对象不同的)k条记录均可与rj组成相遇,通过每次有新记录rj加入的方式来消除滑动窗口之间的重叠,也便于通过选择最早结束相遇的贪心策略直接生成最大有效相遇集合。

3.1 Apriori 性质

获得满足伴随关系的大小为k的对象集合后,本文利用Apriori性质来选择大小为k+1的候选对象集合。Apriori性质的形式化定义见定理1。

定理1(Apriori性质[22])对Oi⊂Oj,有|EL(Oi)|≤|EL(Oj)|。

Apriori性质说明,如果一个对象集合的任意子集不满足伴随关系,则此对象集合不满足伴随关系。因此,可以得到剪枝函数如下:

其中,P(O)=false指O不能通过Apriori性质来判断是否可以剪枝。

3.2 最大相遇集合贪心选择策略

为在保证非重叠性的同时直接选择最大有效相遇集合,本文设计选择最早结束相遇的贪心选择策略。

定义5(最早结束) 给定相遇集合E,如果一个相遇ei∈E满足∀ej∈E,ti,k≤tj,k,称ei是E中最早结束的相遇,此处ei={ri,1,ri,2,…,ri,k},ej={rj,1,rj,2,…,rj,k}。

对当前相遇ei是否最早结束的判断基于与ei有相同对象的所有相遇集合。为获取最早结束的相遇,对所有相遇按结束时间进行检查。对于对象集合O,每次获得尚未加入到最大有效相遇集合的相遇ei,检查ei开始时间是否长于已加入到最大有效相遇集合中相遇的结束时间的最大值,若满足则将ei加入到O的最大相遇集合中,否则抛弃ei,继续检查下一个相遇,这样通过一次扫描即获得所有对象集合的最大有效相遇集合。

3.3 闭合性检查

生成Ck+1后,对Ck进行闭合性检查。如果O∈Ck的超集均不满足伴随关系,则O已闭合。闭合函数定义如下:

3.4 算法基本框架

算法1提供了包含Apriori剪枝、贪心选择策略和闭合性检查的基于滑动窗口的闭合伴随关系挖掘算法基本框架的伪代码。

算法1基于滑动窗口的闭合伴随关系挖掘算法

输入εt,εe,RRec

输出所有满足闭合伴随关系的对象集合CC

1.k=1,初始化C1

2.while Ck≠∅ do

3.C′k+1=Apriori_Generate(Ck)

4.过滤不在C′k+1中对象的记录

5.for li∈LLoc

6.for rj∈Sorted(Rec(li))

7.Greedy_Choose({rk|tk∈[tj-εt,tj]})

8.更新C′k+1

9.过滤C′k+1,得到Ck+1

10.Close_Check(Ck,Ck+1)

11.更新CC

12.k=k+1

13.return CC

对于Ck,k=1时用所有出现次数大于等于εe的对象初始化Ck,k≠1时用Apriori性质进行初始化。算法1第5行的过滤可以减少需要检查的记录的数量,也可以减少需要检查的相遇数量,第8行对大小为k+1的未检查相遇中结束时间最早的相遇进行检查,并对候选集合C′k+1进行更新。检查过所有相遇之后,对频率进行过滤,并挑选闭合伴随关系,开始下一次迭代。假设所有的相遇数量为|NE|,该算法的复杂度即为|NE|。该算法不仅能够有效地生成所有的闭合伴随模式集合,而且可以通过贪心策略进行优化,筛除不能组成最大有效相遇集合的相遇。

基于算法1的基本框架,可给出如图2所示的算法流程。算法在从小到大的宽度优先搜索过程中,分别对每个地点、每个滑动窗口的每个相遇进行检查,检查的主要内容为是否满足贪心条件,添加的剪枝操作也在此处进行,同时在生成候选伴随模式集合和闭合伴随模式集合的过程中会进行闭合性检查。

图2 算法1流程Fig.2 Procedure of algorithm 1

4 2-相遇剪枝算法

在算法1中C1生成C2时,由于C1是所有对象的集合,只能根据每个对象在数据集中出现的总次数进行剪枝,而不能利用任何时空信息(时空信息只在考虑相遇时有用),因此Apriori性质对C2候选集的剪枝效果是最差的,2-相遇具有最高的伪命中率,需要针对2-相遇设计专用的剪枝算法。2-相遇剪枝是指对大小为2的对象集合和相遇集合的剪枝操作,在算法1中用于替代由C1生成C2的过程。添加剪枝操作后的算法框架如图3所示。

图3 加入剪枝操作后的算法流程Fig.3 Procedure of algorithm after adding pruning operations

本文提出的2-相遇剪枝算法是结合了基于哈希的迭代过滤和基于摘要信息的过滤的两层剪枝算法,剪枝的过程随着2-相遇的搜索同时进行。基于哈希的迭代过滤即PCY算法[19],其针对具有相同哈希值的一组对象集合进行剪枝;基于摘要信息的过滤则利用了对象的时空局部性特点求解对象集合的相遇上界进行细粒度的剪枝。

因为基于哈希的迭代过滤和基于摘要信息的过滤分别使用了不同的原理与信息进行剪枝,所以可以结合这两种方法来增强剪枝效果。

4.1 基于哈希的迭代过滤

基于哈希的迭代过滤是将2-相遇对应的对象集合散列到一个哈希空间上,每一个分桶用来计数拥有对应哈希值的2-相遇个数。如果某个计数值小于εe,则说明对应该哈希值的所有对象集合的总2-相遇个数小于εe,他们都是可被剪枝掉的冗余对象集合和冗余相遇集合。在进行一轮剪枝之后,可以对未能剪枝掉的对象集合进行第2轮散列、计数与剪枝,此时由于第一轮被剪枝掉的对象和记录已不再计数,因此迭代可以提供更好的剪枝效果。

以下为基于哈希的迭代过滤的形式化定义:任意一个2-相遇ei={ri1=(oi1,li1,ti1),ri2=(oi2,li2,ti2)},不失通用性,使oi1

PH(ei)=H[h(oi1,oi2)]<εe

Mj=|{ei|h(oi1,oi2)=j}|

若PH(ei)=true,则ei对应的对象集合Oi不能满足伴随关系,因为与ei哈希值相同的相遇总数小于εe。

对于多层的哈希索引,剪枝公式为:

PH(ei)=

基于滑动窗口的算法2用于生成哈希表H。其中,第4行代码确定当前滑动窗口范围[rj.t-εt,rj.t],第5行扫描当前窗口的所有2-相遇,增加对应哈希值的计数。算法2的复杂度同样为|NE|,但由于该算法不存储每个相遇的具体信息,在线性的算法复杂度基础上具有非常小的常数,因此效率较高。

算法2哈希表H生成算法

输入εt,εe,RRec,NH

输出H=[H1,H2,…,HNH]

1.for n ∈ [1,NH]

2.for li∈LLoc

3.for rj∈Sorted(Rec(li))

4.for rk∈Sorted(Rec(li)) and rk.t≤rj.t∧rk.t+εt≥rj.t

5.for n ′∈[1,n)

6.If H′n[h′n(oi1,oi2)]≥εe

7.Hn[hn(oi1,oi2)]+=1

8.return H

在算法2中,可以用额外的哈希表记录单个对象能组成的2-相遇数,从而对记录进行筛选,从而在生成不同层次的哈希表H过程中减少需要比较的记录数量。

4.2 基于摘要信息的剪枝方法

基于摘要信息的过滤计算2个对象能够相遇的次数上界,能够充分利用对象的时空信息。在每个位置l,对象oi和oj有效相遇次数的上界是oi和oj出现在l的较小值,对所有位置的上界加和可得到全局上界B。若B<εe,则oi和oj有效相遇次数小于εe,是可以被剪枝掉的冗余值。进一步可以考虑应用场景中不同的时空特性,通过改变“位置”的粒度,对位置进行聚类或者按时间分割,可以调节计算复杂度与剪枝率之间的权衡。

下面给出基于摘要信息的剪枝的形式化定义。对对象oi,摘要信息S(oi)是记录其在每个位置出现次数的字典结构,形式化定义如下:

S={S(oi)|oi∈OObj}

S(oi)=[(L1,ai,1),(L2,ai,2),…,(LNL,ai,NL)]

ai,j=|{rk|rk=(ok,lk,tk),ok=oi,lk=Lj}|

对于对象集合Oi={oi1,oi2},通过摘要信息S可以计算得到Oi的最大有效相遇集合的上界为:

其中,min{ai1,k,ai2,k}是oi1和oi2在地点Lk的最大有效相遇次数的上界,加和之后得到oi1和oi2的最大有效相遇次数的上界,可以利用此上界进行剪枝:

PS(ei)=B({oi1,oi2})<εe

对于不同的时间长度阈值εt和频率阈值εe,摘要信息S可以复用,不需要重复计算。

在基于摘要信息剪枝的基础上,本文提出2种优化方法:

1)充分利用应用场景的时空特性,改变“位置”的粒度,如将L1、L2与L3组合成分组G1,作为统计摘要信息和计算上界的基本单元,如果|LLoc|很大且S是稀疏的,分组策略可以降低内存消耗,提高算法效率,本文针对不同的应用场景分析特点,提出2种不同的分组策略。

2)提前停止,即如果部分地点的上界和已满足一定条件,则不需要继续计算完整的全局上界。

4.2.1 生成摘要信息的分组策略

首先给出基于分组G={G1,G2,…,GNG}的摘要信息和上界如下:

S(oi)=[(G1,ai,1),(G2,ai,2),…,(GNG,ai,NG)]

ai,j=|{rk|rk=(ok,lk,tk),ok=oi,lk∈Gj}|

本文提出4种不同的分组策略,其中最常用的分组策略是一个位置作为一个组,称为单地点分组策略。单地点分组策略在2种情况下会失效。第1种情况是|LLoc|很大,上界B的计算消耗了主要的时间。第2种情况是位置Lj是一个非常频繁的位置,即|RRec(Lj)|很大,很多对象在Lj的出现次数都临近εe,导致上界B松弛,非常容易达到εe。

针对|LLoc|很大的情况,最直接的方法是将位置按记录数量均匀分组,称为随机分组策略。如果可以从记录中提取连通性信息,也可以将位置基于连通性进行聚类,按照聚类结果进行分组,称为聚类分组策略。在社交网络中,连通性通常对应兴趣点之间的用户转移。对连通性可做如下处理:以位置为顶点初始化构造一张图,对于ri、rj,不妨设ti≤tj,如果oi=oj,li≠lj且tj-ti≤εt,则将li与lj之间边的权重加1,满足上述条件隐含着oi在εt时间内从li移动到了lj,说明li与lj之间很有可能是连通的,权重的大小也能体现li与lj之间通路的频繁使用程度,可以用图上的顶点聚类方法对位置进行聚类,在本文实验中采用层次聚类。

社交网络中的伴随模式挖掘通常具有|LLoc|很大的特征,因为通常网络中的POI的数量比较大,文献[23]中使用的Foursquare数据集在过滤了少于10个用户访问的POI之后有105个POI,而且POI用户访问的稀疏性是非常高的,所以对POI进行分组可以在不影响过滤效果的同时显著缩短计算时间。在进行分组和聚类时可以考虑POI的类别或城市功能区的特点,从而进一步利用数据的空间特性。

针对RRec(Lj)很大的情况,可进一步将RRec(Lj)按时间等分为子记录集合,构成分割分组策略。例如,按时间排序的Lj位置的记录集合RRec(Lj)=[ri,1,ri,2,…,ri,10]可以被划分成RRec(Gj,1)=[ri,1,ri,2,…,ri,5]和RRec(Gj,2)=[ri,6,ri,7,…,ri,10]。需要注意的是ri,5和ri,6有可能会组成相遇,因此,需要对划分的集合保留一定重叠以保证上界成立。

城市道路监控车辆数据集和手机基站接入信息数据集通常具有RRec(Lj)很大的特征,因为监控摄像头和手机基站都可以被动捕捉附近对象的信息。由于车辆和手机的使用者数量都是非常大的,而且不同用户的交通行为通常具有一定的时间规律,例如很多车辆只会在早晚高峰出现,工作日和周末的出现特征不同,因此,分割之后可以显著降低每个组上界的B,从而提高剪枝率。在进行分割时可以充分考虑数据集的规律性,如按照早晚高峰和非高峰时段、工作日和周末进行划分,从而进一步利用数据的时间特性。

在实际使用中也可以堆叠不同的摘要信息进行多层的摘要信息过滤。例如可以采用聚类分组策略和划分分组策略结合的方法,对于数据量小的地点进行聚类,对数据量大的地点进行划分,利用聚类分组策略计算速度快、分割分组策略上界更紧的性质来平衡运算速度和过滤效果。

4.2.2 提前停止

可以使用由前i个分组计算得到的部分上界Bi进行剪枝,定义如下:

在上式中,加号右侧是未检查的分组2个对象各自的出现总次数的最小值,可以在检查每个地点时通过减去当前地点的出现次数来进行更新。部分上界Bi(Oj)具有∀i∈[1,NG],Bi(Oj)≥B(Oj)的性质,因此,如果在计算B(Oj)的过程中发现某部分上界Bi(Oj)<εe,则B(Oj)<εe,Oj可以被剪枝掉,形式化定义如下:

4.3 两层剪枝算法伪代码

算法3给出了2-相遇剪枝算法的伪代码。算法的框架与算法1基本一致,只是在第7行考察是否要贪心地将当前相遇加入到候选集合中前,先后进行了基于哈希的剪枝和基于摘要信息的剪枝以缩减候选集合。

算法32-相遇剪枝算法

输入εt,εe,RRec,NMR,NMC,S

输出C2

1.过滤掉出现次数少于εe的对象

2.调用算法2生成H

3.k=1,初始化C1

4.for li∈LLoc

5.for rj∈Sorted(RRec(li))

6.for rk∈Sorted(RRec(li)) and rk.t≤rj.t∧rk.t+εt≥rj.t

7.If not PH({rj,rk})∧not PS({rj,rk})

8.贪心选择{rj,rk}

9.更新C2

10.Return C2

5 实验结果与分析

实验在单台机器进行,处理器为Intel Core i5-3570 3.4 GHz,内存大小为16 GB,操作系统为64位Windows 8.1,JDK版本为1.8.0_152。

实验在国内某市道路车辆监控车牌识别真实数据集上进行,相关统计信息见表2,由于实验前已对数据进行了清洗和隐私处理,因此表中的时间为采集数据的持续时间,对象数量即不同的车辆数,地点数量即不同的监测点数量。在实验过程中,由于基本算法和其他对比方法[12-13,19]均不含有任何剪枝操作,需要的内存空间超过系统内存上限,估计运行时间比实验中报告的各最差时间慢至少1个数量级(×10),因此在以下部分不单独报告基本算法和其他对比方法的运行时间,与基本算法和其他对比方法的比较通过剪枝率来体现。

表2 测试数据的统计信息Table 2 Statistics information of test data

基于哈希的迭代过滤算法生成了两层哈希表。生成多层哈希表虽然会进一步提高剪枝率,但由于增加了生成哈希表的初始化时间和额外一次哈希检查的时间,运行时间反而会有一定程度减少。实验中报告的所有运行时间均为5次实验的平均值。

5.1 数据集规模对算法性能的影响

图4给出了各算法在不同大小数据集上的运行时间,图5给出了各算法在不同大小数据集上的剪枝率,图6给出了两层剪枝算法在不同大小数据集上各步骤的运行时间,图7给出了各算法运行在不同大小数据上通过过滤的相遇中真实相遇的比例,其中真实相遇指最终组成伴随模式的相遇,即对应伴随模式的最大有效相遇集合。实验中使用的哈希表单层的长度为150 000 000,相遇时间阈值εt=180,相遇次数阈值εe标记在图中。相遇次数阈值εe的选择方法是使算法找到的伴随模式数量大致相同且均不超过1 000,方便在后续寻找犯罪团伙的嫌疑车辆等应用中的人工参与。

图4 不同数据集规模下的运行时间Fig.4 Running time under different sizes of dataset

图5 不同数据集规模下的剪枝率Fig.5 Pruning rate under different sizes of dataset

图6 不同数据集规模下两层剪枝算法各步骤的运行时间Fig.6 Running time of each step of two-layer pruningalgorithm under different sizes of dataset

图7 不同数据集规模下的真实相遇比例Fig.7 True encounter ratio under different sizes of dataset

从图4和图5可以看出,算法在不同规模的数据集上都能够有效地运行,且本文提出的两层剪枝算法具有最低的剪枝率,剪枝率均小于1%。剪枝率的计算方法是通过过滤的相遇个数除以总的相遇个数。总相遇个数是在按照相遇次数阈值对记录进行过滤之后计算出的,过滤的方法是检查每个记录对应的对象在整个数据集中出现的总次数是否小于相遇次数阈值,如果小于相遇次数阈值则将该条记录从数据集中删除。除在15 d的数据集上以外,两层剪枝算法都具有最短的运行时间。在7 d和15 d的数据集上仅利用摘要信息的剪枝方法与其他2种方法的剪枝率相差最小,由于仅利用摘要信息的剪枝方法不需要对不同的参数进行初始化,因此在15 d的数据集上反而具有最短的运行时间。

图5显示了两层剪枝算法各个步骤的运行时间,基于哈希的迭代过滤算法也具有类似的特性。其中:初始化步骤是指初始化哈希表;过滤步骤是指进一步对通过剪枝过滤的对象集合进行检查,找到真实的伴随模式;生成步骤是指从大小为2的伴随模式生成更大的伴随模式的过程。从图5中可以看出,初始化过程占据了多数运行时间。此外,随着数据集的增大,生成过程所用的时间也逐渐增加。

图7显示了通过剪枝过滤的相遇中真实相遇的比例,可以看出两层剪枝算法中真实相遇比例是最高的,均超过了50%。

5.2 摘要信息分组策略对算法性能的影响

图8和图9显示了不同的摘要信息分组策略下算法的运行时间和剪枝率。实验是在7 d的数据集下运行的,相遇时间阈值εt=180,相遇次数阈值εe=38,哈希表单层的长度为100 000 000。后缀 O 指单地点分组策略,S 指分割分组策略,G200指分为200组的随机分组策略,C200指分为200组的聚类分组策略。从图8可以看出,两层剪枝算法运行时间最短。在两层剪枝算法中使用聚类分组策略可达到最短的运行时间,因为在两层剪枝算法的剪枝率都很高的情况下,聚类分组策略的计算代价较小。在不同分组策略的横向比较中,组数越多剪枝率越高。聚类分组策略由于可以利用空间局部性,效果比随机分组策略好。通过图8与图9的比较也可以看出,运行时间与剪枝率成正比,剪枝率越高,运行时间越短。

图8 摘要信息分组策略对运行时间的影响Fig.8 Influence of summary information groupingstrategies on running times

图9 不同摘要信息分组策略下的剪枝率Fig.9 Pruning rate under different summary informationgrouping strategies

5.3 相遇次数阈值对算法性能的影响

图10～图13显示了不同相遇次数阈值下算法的运行时间和剪枝率。实验是在7 d的数据集下运行的,相遇时间阈值εt=180,哈希表单层的长度为100 00 000。

图10 相遇次数阈值对运行时间的影响Fig.10 Influence of thresholds of encounter time on running times

图11 不同相遇次数阈值下两层剪枝算法各步骤的运行时间Fig.11 Running time of each step of two-layer pruningalgorihm under different thresholds of encounter time

图12 不同相遇次数阈值下的剪枝率Fig.12 Pruning rate under different thresholds ofencounter time

图13 不同相遇次数阈值下的真实相遇比例Fig.13 True encounter ratio under different thresholds ofencounter time

从图10可以看出,除最高的42次相遇次数阈值之外,两层剪枝算法都具有最短的运行时间。当相遇次数阈值为42时,由于比较高的相遇次数阈值使得候选对象集合减少、剪枝率提高,且基于摘要信息的剪枝算法不需要初始化时间,基于摘要信息的剪枝算法运行时间最短。从图11可以看出,随着相遇次数阈值的提高,初始化时间逐渐稳定,且占据了两层剪枝算法多数的运行时间。从图12可以看出,两层剪枝算法和基于哈希的剪枝算法的剪枝率随相遇次数阈值提高而有所下降,主要是因为随着相遇次数阈值的提高,候选对象集合的数量有所下降。而对基于摘要信息的剪枝算法而言,剪枝率随相遇次数先降后升,主要是由于在相遇次数阈值提高时,基于摘要信息的剪枝算法的剪枝效果更为明显。从图13可以看出,两层剪枝算法仍具有最好的剪枝效果,真实相遇比例基本稳定在50%以上。

5.4 相遇时间阈值对算法性能的影响

图14～图17对在不同相遇时间阈值下算法的运行时间和剪枝率进行了介绍。实验是在7 d的数据集下运行的,相遇次数阈值εe=30,哈希表单层的长度为100 000 000。

图14 不同相遇时间阈值下的运行时间Fig.14 Running time under different thresholds ofencounter time

图15 不同相遇时间阈值下两层剪枝算法各步骤的运行时间Fig.15 Running time of each step of two-layer pruningalgorithm under different thresholds of encounter time

图16 不同相遇时间阈值下的剪枝率Fig.16 Pruning rates under different thresholds ofencounter time

图17 不同相遇时间阈值下的真实相遇比例Fig.17 True encounter ratio under different thresholds ofencounter time

从图14可以看出,除最低的90 s相遇时间阈值之外,两层剪枝算法都具有最短的运行时间。在最低的相遇时间阈值时基于摘要信息的剪枝算法具有最短的运行时间的原因与图10中相遇次数阈值为42的情况类似,都是因为候选对象集合的数量较少,而基于摘要信息的剪枝算法不需要初始化时间,因此整体运行时间较短。图15中各个步骤的运行时间比例也体现出,随着相遇时间阈值的提高,剪枝步骤所占据的时间逐渐提高。从图16和图17中可以看出,在不同相遇时间阈值下,两层剪枝算法具有最高的剪枝率,且通过两层剪枝算法过滤后的相遇中真实相遇比例也最高。

6 结束语

公安犯罪团伙嫌疑车辆分析、基于地点的社交网络用户推荐等应用具有时间连续、空间离散、时空相关、数据量大的特点,针对此类场景中的移动对象相似性挖掘需求,本文研究移动对象的伴随模式挖掘问题,构建基于Apriori框架和贪心选择的算法框架,提出一种结合基于哈希迭代剪枝和摘要信息剪枝的两层剪枝算法,以解决中间结果过多的问题,提高挖掘效率。基于真实数据的实验结果表明,本文算法可以稳定去除99%以上的中间数据。为进一步提高算法的可扩展性,后续将基于Apache Spark[20]等分布式计算平台实现算法及相应的剪枝策略,以应对分布式情景带来的挑战。