一种维持约束网络相容性的双向传播策略
2020-04-20司怀伟郭宗沂李东雨谭国真
李 晓,司怀伟,郭宗沂,李东雨,谭国真
(大连理工大学 电子信息与电气工程学部,辽宁 大连 116024)
0 概述
约束网络满足弧相容(Arc Consistency,AC)要求,对于任意变量,变量论域中的任何取值可以在任意包含该变量的约束中找到支持。在回溯搜索中维持弧相容是求解约束满足问题常用的对搜索减枝的技术[1]。研究人员提出用于实现弧相容的算法,其中,AC3粗粒度弧相容算法及其扩展算法维持了一个需要修订的元素列表,在初始阶段将约束网络中的所有变量(或约束,取决于采用的传播策略)加入到列表中,然后迭代取出对列表中的元素执行修订,将修订过程中引入的需要修订的元素重新加入到列表中,当列表为空时,当前满足连通性的约束网络实现弧相容[2]。AC3粗粒度弧相容算法使用轻量数据结构并且易于实现,因此被广泛用于回溯搜索解决方案[3]。
在维持相容性的过程中,可以将修订应用于变量、弧或约束,依此可以分为基于变量的传播策略、基于变量间约束关系的传播策略和基于混合变量关系(弧)的传播策略,不同传播策略维持的待修订的元素列表分别有不同的实现[4]。基于变量的传播策略维持一个待修订变量的集合,集合中每个变量所在的约束关系均是相容性被打破的约束,算法按照一定的顺序从集合中取出变量并维持其所在约束的相容性,同时将维持当前约束相容性而修改论域的变量放入集合,直到集合为空。当前网络实现相容性或证明当前网络不满足相容性,通常以任一变量论域删除来识别当前网络不满足相容性,即该网络无解。使用一个集合维持当前待维持相容性的变量,不必在每次维持相容性时完整地扫描整个网络,因而是一个增量维持相容性的过程,基于约束的传播策略和基于弧的传播策略均是采用这种增量维持相容性的过程,因而也维持一个待更新的元素的集合,只是基于约束的传播策略维持的是约束,基于弧的传播策略维持的是弧,3种传播策略分别实现了不同的识别并避免冗余传播的优化手段,具体请见文献[3]。实验结果验证,基于变量传播策略的算法实现通常有较为优秀的性能表现[3,5]。本文提出的双向传播策略在维持相容性时同样维持的是待修订的变量的集合,但将当前变量所在约束上的相容性维持分成2个独立的阶段,这种分阶段维持相容性可以有效避免一些冗余传播,综合求解性能优于现有的基于变量的传播策略。
列表中元素的处理顺序对修订的效率具有显著影响[5],因此对其有效排序并进行修订是使用时序计数的主要目的。修订效率上产生的影响将由核心运算单元得到的计算时间反映出来。研究者已经提出了多种修订排序启发式方法,首先利用约束网络的信息,例如变量域范围区间、约束阶数和允许的值组合对列表中的元素进行排序,dom/ddeg启发式是一种动态的启发式排序算法,按照当前变量域大小对变量进行排序,对提高算法效率有重要作用[6]。dom/ddeg与AC3粗粒度弧相容系列算法的基于变量间关系或基于混合变量关系的传播方案同时应用是目前先进的传播策略,主要用于解决弧相容算法的加速问题[7]。在文献[7]中,基于变量的方案与dom/ddeg修订排序启发式集成,可以显著减少约束检查的数量。在文献[8]中,有关约束权重的信息用于对列表中的元素进行排序,不仅减少了约束检查和表约束[9]的数量,还可以减少已探索搜索树的大小压缩解空间[10]。
文献[11]结合路径一致性给出一种解空间压缩方式,这种解空间压缩方式缺点在于得到加权有向图的过程属于一种紧凑表示过程,当缩小权值范围时导致部分可行解丢失,没有维持满足性条件。目前关注较多的约束满足性问题的求解技术包括简单表缩减STR、MDDC技术,是约束关系压缩表示技术[12]。基于约束关系的表约束过滤算法的传播队列包含必须重新修订的约束信息[13]。文献[14]建立了一种基于关系的软约束模型,使用搜索方法探索解空间,适合处理少量变量的情况。文献[15]使用搜索技术提出了并行的维持局部一致性的方法,但是由于时间代价大,尚未被广泛应用在求解中。文献[16]提出按位运算的表压缩过滤算法有效压缩处理元组,这种基于表约束的边界处理方法使压缩过程明显加速。
本文基于增量的更新子网的方式,提出一种新的基于时序计数的传播方案,将accumulateRevision和pushRevison作为双向修订的主要过程,并通过文献[1]测试集进行实验。
1 研究背景
一个约束网络是一个元组(X,C),其中,X={x1,x2,…,xn}是一个n个变量的集合,C={c1,c2,…,cm}是m个约束的集合。每个变量xi有一个域值dom(xi),代表变量xi可行的取值集合。每个约束ci有一个约束范围scp(ci)和一个关系rel(ci),其中scp(ci)是X的子集,并且rel(ci)是scp(ci)中满足ci的元组的集合。一个二元约束只涉及2个变量,将一个xi和xj之间的二元约束描述为cij。如果2个变量共享一个约束那么被称为邻居。一个弧是一个对(cij,xi),其中xi∈scp(ci)。当关注二元约束时,任何弧(cij,xi)可以表示为满足xi,xj∈scp(cij)的变量对(xi,xj)。
弧(xi,xj)是AC或xi关于cij满足AC的当且仅当对每一个a∈dom(xi),存在一个值b∈dom(xj),使得(a,b)满足cij。在这种情况下,称b在cij上支持a。一个弧(xi,xj)的修订或者说与xi有关的cij需修订保证dom(xi)所有值都支持dom(xj)。一个约束网络是弧相容当且仅当变量没有空域并且所有的弧都满足弧相容。弧相容算法从dom(xi)删除所有与不支持xi的约束。
约束满足问题(CSP)的实例由约束网络定义。一个约束满足问题是可满足的当且仅当存在至少一组解,否则该约束满足问题无解。解决CSP问题的实例涉及找到一个(或多个)解决方案或确定其不可满足性。解决方案为所有变量赋值,以使所有约束都是满足的。
1.1 基于约束关系的传播策略
基于约束关系的传播策略存储以变量之间的关系为主,主要包括存储弧和非单纯变量,修订时占用的存储空间比基于变量的存储空间大。基于纯变量之间关系cij的传播策略以变量之间的弧为传播存储单元,在FIFO结构中,每个关系也即弧单元(xi,xj)存储到列表中,依次弹出队列进入修改区,如果弧单元(xi,xj)已被修改,即修订标记Reivise中DELETE元素的布尔属性反转为True,那么将新的弧单元(xk,xi)作为新的修订内容,即做再次修订。在初次正向修订时,对弧中所有关系考察变量赋值,遍历所有变量取值某个变量xi,若不存在任意一个满足弧的取值,那么将此变量从弧关系中删除,发生一次修订,记录一次DELETE反转。
1.2 基于混合变量关系的传播策略
在基于混合变量关系的传播策略中,存储单元为变量之间的关系,即弧和涉及变量,简写为(cij,xj),可以使用累加计时器CTR(cij,xi)避免冗余修订,本文引入辅助参数needsNotBeRevised支持混合变量关系(cij,xj)的筛选和修订,若needsNotBeRevised为真,那么忽略此修订,否则将revise(cij,xj)赋给nbRemoval,如果nbRemoval(cij,xj)>0,那么判断xj的域空间是否清空,如果域空间为空,那么此变量不满足弧相容,在涉及此变量的所有相关关系的约束处理上,即对满足cjk|cjk≠cij∧xj∈vars(cjk)的变量xj,将其放入队列结构。CTR累加转变为:ctr(cjk,xj) ←ctr(cjk,xj)+nbRemovals。这是基于混合变量的单一循环结构。
1.3 基于变量的传播策略
当Q为空或变量域消失时,AC算法终止。在3种传播方案中,基于变量的方案优于其他2种方案。在文献[18]中,CTR是某个事件发生的时间计数器,随时间跟踪算法的进度识别冗余修订。本文在基于变量的传播策略上运用时序计数标记,每个变量的时序计数CTR标识一个全局唯一的计数,表示该变量论域最新发生修改的事件,每个约束的时序计数表示该约束最新满足弧相容的时间[17]。
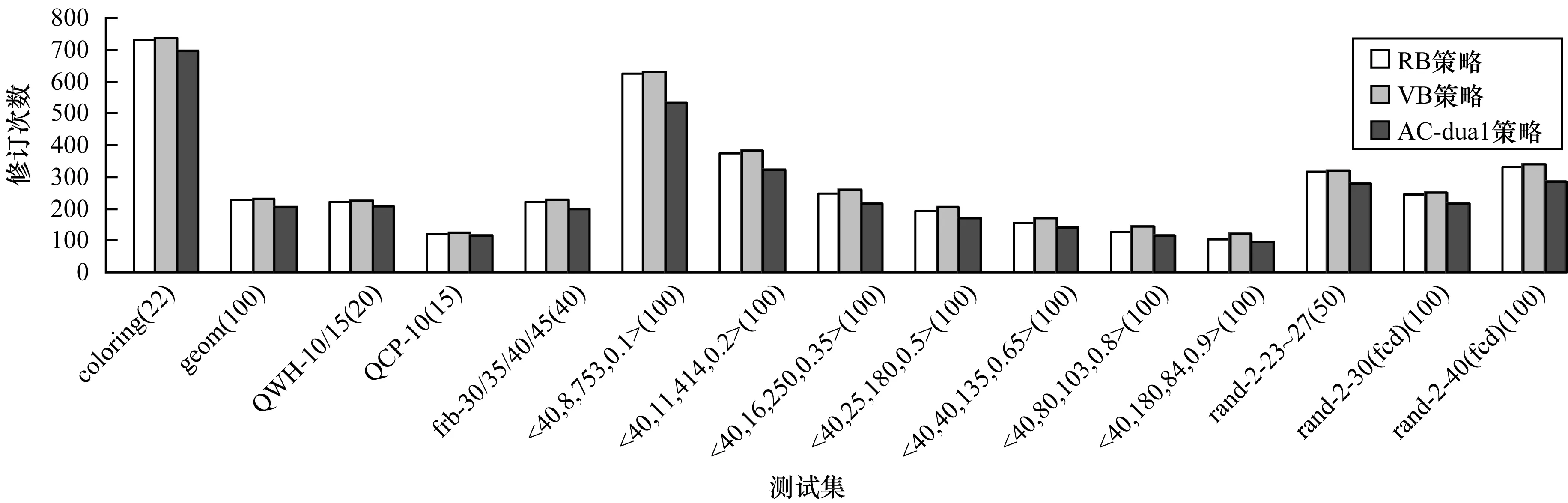
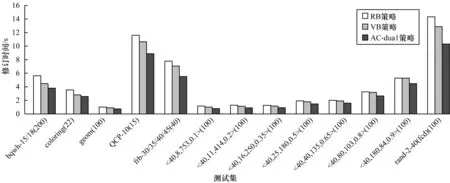
为了简化描述,本文使用revise(xi,xj)表示在xi上与cij相关的修订。当在一个约束cij上建立弧相容时,如果CTR[xi]>CTR[cij],那么revise(xi,xj)是必要的,否则,revise(xi,xj) 是冗余的。在现有的采用时序计数检测冗余revision的传播策略中,假设cij是待处理的约束,存在一种情况,xi是最新从Q中取出来的变量,并且存在CTR[xi]>CTR[cij],而xj先于xi被处理并且存在CTR[xj] 在基于二元约束首尾变量的传播策略中,修订列表存储的是变量xi,xj,xk,…,在队列queue或其他数据结构中初始化列表存储这些变量。依次从基本数据结构中弹出每个变量,对每个涉及的变量xi及其约束满足eachcij|xi∈vars(cij)进行修订。累加计数器CTR用于识别冗余,∀cij∈C,∀xi∈vars(cij),CTR置为1,依然引入辅助参数needsNotBeRevised,返回逻辑运算单元(ctr(cij,xi)>0 and ∃xj∈vars(cij) |xj≠xi∧ctr(cij,xj) > 0),支持混合变量关系(cij,xj)的筛选和修订,如果needsNotBeRevised为真,那么忽略此修订,否则将revise(cij,xj)赋给nbRemoval;如果nbRemoval(cij,xj)>0,那么判断xj的域空间是否清空;如果域空间为空,那么此变量不满足弧相容,在涉及此变量的所有相关关系的约束处理上,即对满足cjk|cjk≠cij∧xj∈vars(cjk)的变量xj,将其放入队列结构。CTR累加至ctr(cjk,xj) ←ctr (cjk,xj)+nbRemovals,对所有满足x∈vars(cij)的变量 ctr (cjk,xj)置0。当从传播集合Q中选取变量xi时,现有的基于变量的方案依次处理与xi相关的约束,对每个约束的处理包括修改约束中涉及的弧。 双向传播策略算法如算法1~算法6所示。 算法1AC3-dual算法 begin 1.Q←{xi| xi∈ X}; 2.∀cij∈C,CTRs[cij]← 0 3.∀xi∈X,CTRs[xi]← 1 4.while Q ≠∅ do 5. pick and delete xifrom Q 6. If xi∈past(P) then 7. Continue; 8. accumulateRevision(xi) 9. pushRevision(xi) 10.Return true; end 算法2accumulateRevision(xi)算法 begin 1.for each cij| xi∈ scp(cij) ∧ CTR[xj] > CTR[cij] do 2. if revise(xi,xj) then 3. if dom(xi) =∅ then 4. clear Q(xi); 5. return false; 6. CTR = CTR[xi]; 7. setCTR(xi); 8. if CTR[cij] > CTR then 9. setCTR(cij); end 算法3pushRevision(xi)算法 begin 1.for each cij | xi ∈ scp(cij) ∧ CTR[xi] >CTR[cij] ∧ xj∈ past(P) do 2. if revise(xj,xi) then 3. if dom(xi) =∅ then 4. clear Q(xi); 5. return false; 6. Q← Q ∪ {xj}; 7. setCTR(xj); 8.setCTR(cij); end 算法4revis e(xi,xj)算法 begin 1.for each a ∈ dom(xi) do 2. if seekSupport(xi,xj,a) = false then 3. remove a from dom(xi); 4. return true; 5.return false; end 算法5setCTR(m)算法 begin 1.CTR = CTR + 1; 2.CTR[m] = CTR; end 算法6clearQ(x)算法 begin 1.CTR[x] = 0; 2.while Q ≠ ∅ do 3. pick and delete xifrom Q; 4. CTR[xi] = 0; end 算法1给出了一种基于二元约束首尾变量的双向传播方案——AC3-dual,AC3-dual将维持相容性的修订操作分为2个独立的阶段。past(P)是约束网络P中已实例化变量的集合,如果检测到约束网络P不是弧相容的,则返回false,否则返回true。 算法2对应AC3-dual的第1阶段。该阶段变量xi迭代xi的所有邻居约束寻找支持,当a∈dom(xi)在任意一个约束中无法找到有效支持时,从dom(xi)中删除a。本文利用时序计数标记变量与约束被修订的先后顺序,只有CTR[xj]>CTR[cij]的弧(xi,xj)被修订。当修订是有效时(至少一个值从dom(xi)中删除),并且dom(xi)为空,说明在该次修订中,dom(xi)中所有值均在至少一个约束中没有有效支持,因此当前网络不满足相容性,算法调用clearQ,清空传播集合Q,并且返回false,表示当前赋值序列产生的约束网络无解,触发上层搜索算法回溯,撤销导致无解的赋值。当修订是有效的,并且dom(xi)没有被删空时,CTR[xi]被更新,表示dom(xi)被更新是最新的操作。注意到如果在更新CTR[xi]之前,CTR[cij]>CTR[xi],说明约束cij在xi修改了与cij有关的约束后已经是弧相容。在这一步更新CTR[cij]从而使得CTR[cij]>CTR[xi],避免在与cij相关的xj的冗余修订。 算法3对应AC3-dual的第2阶段。所有xi的邻居节点满足CTR[xi]>CTR[cij],并根据cij进行修订。由于xi在第1阶段根据所有xi的约束进行修订,并且dom(xi)的规模在当前传播中不再修改,寻找一种在xi上的支持非常必要。执行修订后,如果dom(xj)为空,表示当前网络不滿足相容性,当前赋值序列无解,算法调用clearQ(x)并返回false,否则,xj被添加到Q中并且设置CTR [xj]将dom(xj)的修改标记为最新的操作。最终约束cij变为弧相容,并且CTR[cij]被更新。 在AC3-dual中,在修订变量xi及其所有邻居后,涉及xi的所有约束都是弧相容(AC)的,这是AC3-dual与现有的基于变量的方案之间的主要区别。为了更好地说明,本文给出以下示例。 图1是一个二元CSP的子网络。假设所有包含x1的约束依c12,c13,…,c16进行处理。x1被选出并且从Q中删除,变量的时序计数和约束如下:CTR[x2] < CTR[c12],CTR[x3] < CTR[c13],CTR[x4] > CTR[c14],CTR[x5] < CTR[c15],CTR[x6] > CTR[c16]。 图1 二元约束CSP的一个子网络 在现存的基于变量的传播策略中,如果在处理c14时dom(x1)减小,则违反了在c14之前处理的所有约束的一致性,并且需要对它们进行进一步的修改,因此x1再次被添加到Q中,这种情况会在处理c16时再次发生。最终,在修改x1及其所有邻居之后,涉及x1的约束不保证弧相容且x1可能仍然在Q中。在约束网络上应用算法1时,所有k= 2,3,…,6的弧(x1,xk)在第1阶段中满足弧相容,因此dom(xi)在当前传播中不再减小。然后所有k= 2,3,…,6的弧(xk,x1)在第2阶段中满足弧相容。因此,在修改x1及其所有邻居之后,所有涉及x1的约束都将成为弧相容,而x1将不会再次添加到Q中。 当检测到约束网络不满足相容性时(算法2的第3行以及算法3的第3行),发生回溯。约束网络需要恢复到先前的弧相容状态。时序计数标记针对变量或约束的操作在全局上的先后顺序,这种数据结构相对回溯搜索是稳定的[18],即搜索算法发生回溯时并不需要将时序计数恢复为原来的状态,因此也不需要对搜索各阶段的时序计数备份,但是为了避免冗余修订,所有的时序计数CTR[xi]应该设置为小于所有时序计数CTR[cij]的整数[9]。本文将搜索期间约束网络的所有变量划分为3个组。第1组包括Q中的变量;第2组仅包括最近从Q中挑选的一个变量;第3组包括所有其他变量。在理解了AC执行的过程之后,如果至少存在约束cij使得CTR [xi]> CTR [cij],那么xi必须属于第1组或第2组。因此,当回溯发生时,只需要处理属于组1或组2的变量的时序计数来实现。特别地,相关变量的标记CTR[xi]需要设置为小于所有标记CTR[cij]的整数。这是通过算法3中的clearQ(x)的程序完成的,该操作可以直接将时序计数CTR[xi]设置为0。 AC3-dual的时间复杂度主要取决于修订启发式的结构,对于二元约束的数据集存在的e个约束关系,假设每个约束的约束关系包含的2个变量的论域大小为m、n,则每个约束的修订复杂度为O(mn),为了便于观察数量级,令m=n=k,则每个变量的修订复杂度为O(k2),使用dom/ddeg动态决策启发式一定程度上会减小修订操作的计算量,但最坏时间复杂度仍与queue相同,为O(ek3)。 本文实验是在3.20 GHz Intel 8thcore i5处理器上运行,内存为8 GB。图2为使用基于约束关系、基于混合变量关系和基于变量的双向传播策略,这3种策略应用queue在不同测试集的修订次数的平均对比结果。图3为3种传播策略使用dom/ddeg在不同测试集的修订次数。图4给出3种传播策略使用queue在不同测试集的修订时间。图5给出3种传播策略使用dom/ddeg在不同测试集的修订时间。本文测试了超过1 600个实例,并在有限的600 s时间内区分是否超时,有关测试实例的详细信息可以在C.lecoutre的主页上找到。 图2 3种传播策略使用queue在不同测试集上修订次数的对比结果 图3 3种传播策略使用dom/ddeg在不同测试集上修订次数的对比结果 图4 3种传播策略使用queue在不同测试集上修订时间的对比结果 图5 3种传播策略使用dom/ddeg在不同测试集上修订时间的对比结果 本节通过对比不同传播方案的修订时间和修订次数研究了本文传播策略。其中,AC3-dual表示本文提出的传播方案,RB表示经典的基于关系的方案,应用ctr来识别冗余修订,VB表示应用时间戳[18]的基于变量的传播方案。回溯搜索采用的变量排序启发式是dom/ddeg[6],值排序是按照字典序的排序方式。 在2种revision启发式中,即queue启发式和dom/ddeg启发式,AC3-dual采用的传播策略在扩展单个节点的平均revise次数,即算法在求解时调用算法4的总次数除以总扩展节点数,总是小于VB和RB中的revise次数,这说明AC3-dual采用的传播策略在保证相容性不变的同时,的确降低了算法执行revise的次数,原因已经在本文第3节做了分析。AC3-dual在实例集<40,8,753,0,1>上降低revise操作的效果比较明显,这是因为在<40,8,753,0,1>上表示的约束网络含有大量的环,导致VB和RB在执行revise时,会频繁地由邻居节点传向自身,增加了在维持相容性时的revise操作,AC3-dual运行在该类存在大量环的网络中时,先执行accumulateRevision,确保所有由邻居节点改变带来的对该节点的修订都已经完成,再执行pushRevision,将对该节点的修订引起的网络的变化更新到所有邻居节点上,在网络上存在较多环时,部分避免了对当前节点的修订操作会频繁地通过邻居传回自身。 从图4和图5可以看出,无论在queue启发式还是在dom/ddeg启发式中,AC3-dual降低revise操作数量带来了求解效率的提升,AC3-dual在上述问题上的修订时间均小于VB和RB,对于revise操作降低比较明显的实例集,求解效率提升较为显著,这说明AC3-dual采用的传播策略在降低revise操作的同时,没有带来太多额外的计算代价。 本文提出一种新的基于时序计数的传播方案。该方案保留了在建立弧相容时需要修改的变量列表,并与修订列表的启发式相结合,在域过滤过程中进行双向修订,减少修订次数和域过滤变量的数量。实验结果表明,加入启发式的双向修订及应用时序计数的排序方法,提高了该传播方案在整体求解速度和占用修订时间性能。虽然本文弧相容传播策略在大量问题实例中速度明显提升,但主要是应用在二元约束背景中,下一步将本文传播策略应用到多元约束满足问题,为基于问题重构的高阶相容性[20]引入新的删除冗余的方法,以降低维持弧相容的代价。2 基于变量的双向传播策略
2.1 双向传播策略算法
2.2 双向传播示例

2.3 时间复杂度
3 实验与结果分析


4 结束语
