黑河金盆水库坝区三维渗控效应评价与材料参数敏感性分析

周邠鹏， 柴军瑞， 雷 艳

(1.西安理工大学， 陕西 西安 710048； 2.中国电建集团西北勘测设计研究院有限公司， 陕西 西安 710065)

1 研究背景

土石坝的渗流控制是减小地下水渗漏，降低地基、围岩及坝体渗透压力进而改善其渗透稳定性最重要的工程措施。土石坝工程中主要的防渗措施包括防渗墙、防渗面板、防渗帷幕和防渗铺盖等。为了揭示各种渗流控制措施的物理机制和渗流控制效应，进而评价工程的安全稳定，需要对工程区渗流场及防渗系统的渗控效应进行精细模拟。

大量研究者已经采用有限元方法对土石坝的渗流分析开展研究。刘豪杰等[1]、江浩源等[2]、温立峰等[3]、王正成等[4]研究了深厚覆盖层上土石坝渗流控制技术，系统分析了覆盖层地基的渗流控制效应。毛海涛等[5]对无限深透水地基上土石坝的渗控效应开展了评价研究。陈守开等[6]采用节点虚流量法对中、小型土石坝渗流场开展了渗流分析。岑威钧等[7]采用剔除单元法和渗透系数放大法对土石坝进行了饱和-非饱和三维渗流场有限元数值模拟，研究了土工膜不同缺陷对大坝整体及局部渗流场的影响。涂扬举等[8]对瀑布沟土石坝进行了渗流分析，计算了影响渗流安全关键部位的水力坡降。此外，沈振中等[9]、金建峰等[10]对土石坝的绕坝渗流进行了计算和分析。已有研究较多地集中在土石坝枢纽工程的单体结构方面，比如覆盖层上的大坝、大坝两岸的山体等。而评价土石坝工程的渗控效应，进而分析其安全稳定，需要对整个枢纽区进行精细模拟。

有限元数值分析方法是渗控效应评价的主要手段，其主要难点在于渗流场的精细模拟。渗流场的精细模拟的主要要点是溢出点和自由面的确定，应属强边界非线性问题。目前渗流自由面的有限元数值模拟方法包括初流量法、剩余流量法、渗透系数调整法等方法[11-14]以及有着更严密理论基础的变分不等式方法[15-17]。其中，Zheng Hong等[17]建立的Signorini型变分不等式提法，在理论上消除了出渗点的奇异性和由此引起的网格依赖性，在实际工程中应用效果良好。陈益峰等[18]基于Signorini型变分不等式方法建立了分析含复杂渗流控制系统的稳定-非稳定渗流分析的SVA方法。Signorini型变分不等式方法较多运用于地下厂房围岩渗控效应的分析和优化设计中，并已得到工程验证[19-20]，但是在土石坝枢纽渗流分析与评价中较少运用。

本文采用Signorini型变分不等式方法对黑河金盆水库坝区渗控效应进行精细模拟。通过建立枢纽区三维有限元模型评价了枢纽区渗流控制效应和安全稳定性，进而开展了枢纽区渗流场对黏土心墙、防渗帷幕及山体渗透性的敏感性分析。

2 渗流分析的变分不等式方法

渗流分析的变分不等式方法通过将传统方法只对湿区定义和分析渗流问题，扩展到包含干区的整个区域上，并采用Signorini型互补条件描述潜在溢出边界，即可采用理论基础更加严密的Signorini型变分不等式方法求解含自由面的渗流问题[17]。

为了完成对饱和渗透系数ks(m/s)按照公式(1)和公式(2)的调整，在变分不等式方法引入Heaviside阶跃函数H(φ-z)作为相对渗透系数kr：

k=krks=H(φ-z)ks

(1)

(2)

式中：φ为总水头，m；φ=z+p/γw；z为位置水头,m；ε0为一任意小的值；Ωw为湿区；Ωd为干区。

在Darcy定律中，饱和区渗透系数取ks，非饱和区取为0，再将求解域由仅湿区Ωw扩大到全域Ω。改变定义后的Darcy定律可用公式(3)表示：

v=-ks▽φ+v0

(3)

式中： ▽为梯度算子；v为水渗流的速度，m/s；v0为最始流速,m/s，通过引入v0来消除干区Ωd上的虚假渗流场。

上述各式中若φ与时间无关，则相应的控制方程和边界条件退化为稳定渗流情况。公式(1)～(3)应满足下列边界条件：

(1)水头的边界条件

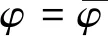
(4)

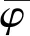
(2)流量的边界条件

(5)

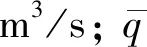
(3)溢出面Signorini型互补边界条件

(6)

(4)自由面边界条件

qn|Ωw=qn|Ωd=0

(7)

针对上述偏微分方程提法，Zheng Hong等[17]和Chen等[15-16]分别建立了针对稳定渗流和非稳定渗流的抛物线型变分不等式提法。这种提法将溢出面Signorini型互补边界条件与自由面边界条件全部转化为自然边界条件，从而大幅度降低了选取试探函数的难度，该方法与偏微分方程提法在理论上是完全等价的。

3 工程概况

西安市黑河金盆水库位于周至县境内黑河峪口以上1.5 km处。该工程于1996年开工建设，2003年5月开始蓄水试运行。水库正常蓄水位594.00 m，死水位520.00 m，总库容2.0×108m3，坝后电站装机量200 MW。枢纽主要建筑物由黏土心墙砂卵石坝、泄洪洞、溢洪洞、引水洞、坝后电站、左岸单薄山梁防渗处理及副坝等组成。

拦河坝为黏土心墙砂卵石坝，最大坝高为128.90 m，坝顶高程600.00 m，坝顶长443.63 m，坝顶宽度11.00 m。上游坝坡1∶2.2，下游坝坡1∶1.5。坝体典型剖面图1所示。心墙防渗体坐落在弱风化岩石上；上、下游坝壳河床段座落在砂砾石覆盖层上，两岸置于清基后的岩面上。枢纽工程水泥帷幕防渗工程包括心墙基础(含两岸坝肩)、单薄山梁和副坝防渗帷幕灌浆3部分。心墙基础防渗帷幕采用封闭式帷幕，设计标准为单位吸水率q≤3 Lu，帷幕轴线与坝轴线重合，主帷幕孔深一般在40～80 m之间。两坝肩岸幕采用单排孔帷幕，最大孔深位于左坝肩为105 m，右坝肩最大孔深75 m。单薄山梁防渗位于大坝左岸金盆北山梁，帷幕灌浆轴线长1344.98 m，防渗帷幕按单排孔设计，孔距2 m，起灌高程为600.00 m，孔底高程为520.00 m高程。单薄山梁防渗标准为q≤5 Lu。副坝坝基防渗帷幕与单薄山梁防渗帷幕线相接，帷幕设计标准为q≤5～8 Lu。

枢纽区布置了渗流监测系统用于监测坝体和坝基渗透压力、渗流量、绕坝渗流。坝体渗流压力采用渗压计监测。在桩号0+088、0+316和0+225 m断面心墙和上、下游坝料中不同高程共布置21个测点。坝基渗流压力采用渗压计监测，在桩号0+088、0+225、0+316 m心墙与混凝土垫层之间和桩号0+225 m心墙混凝土垫层与基岩之间的帷幕上、下游共布置37个渗压计测点。典型断面的渗压计布置如图1所示。左、右岸山体采用地下水位监测孔观测地下水位，总共包含30个观测孔。采用量水堰测量各关键部位的渗流量。

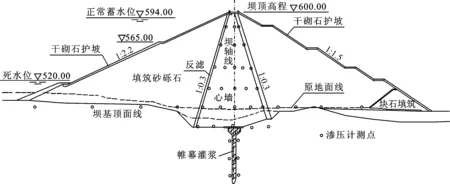
图1 黑河金盆水库黏土心墙坝典型剖面图

4 计算模型

4.1 计算模型和边界条件

采用变分不等式方法对黑河金盆水库库区进行渗流分析与计算。三维渗流计算模型以河流横向为x轴，指向左岸为正；以河流流向为z轴，下游方向为正；以垂直水平面方向为y轴，垂直向上的方向为正。坐标原点选取在大坝轴线河床中点位置的0标高处。模型计算范围取为上游边界为防渗线上游200 m，右边界为右岸灌浆隧洞端头以右200 m，左岸边界应包括左岸灌浆隧洞、单薄山梁和副坝，下游边界为下游坝脚以外400 m，基础边界为河床坝基帷幕以下200 m。

采用三维八节点六面体等参数单元模拟各分区渗流。网格划分中，对黏土心墙、防渗帷幕以及坝体等重点部位网格进行了适当加密处理，对计算结果影响较小的周围山体及大坝基础部位的网格采用适当过渡、减密处理。有限元模型总共剖分416 728个节点，390 521个单元，计算模型如图2所示。模型上游施加上游水头边界；对于下游及坝体下游水位以上施加潜在出渗边界，其余施加下游水头边界；左、右两侧以及底部均施加不透水边界。

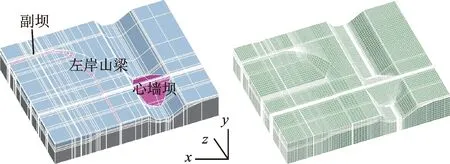
图2 有限元计算模型

4.2 计算参数

黑河金盆水库三维渗流计算分析考虑区域内涉及的所有材料分区，共5种。各不同材料分区的渗流计算参数根据现场原位试验，采用试坑法确定，在此基础上类比相似工程渗透参数，再对试验获得的渗透系数进行修正，从而确定最终参数，具体取值如表1所示。

表1 各材料分区渗流计算参数

5 结果分析

5.1 不同运行状态下渗流场分布规律与评价

为了分析不同水位运行状态下的水库坝区渗控效应，分别计算了死水位、正常蓄水位和校核洪水位情况下渗流场的分布规律。正常蓄水位情况下，x=0剖面(坝体最大剖面)和y=488.5 m剖面(建基面剖面)的水头等值线如图3和4所示。坝体坝基面典型位置处的总水头和水力坡降分布规律如图5和6所示。

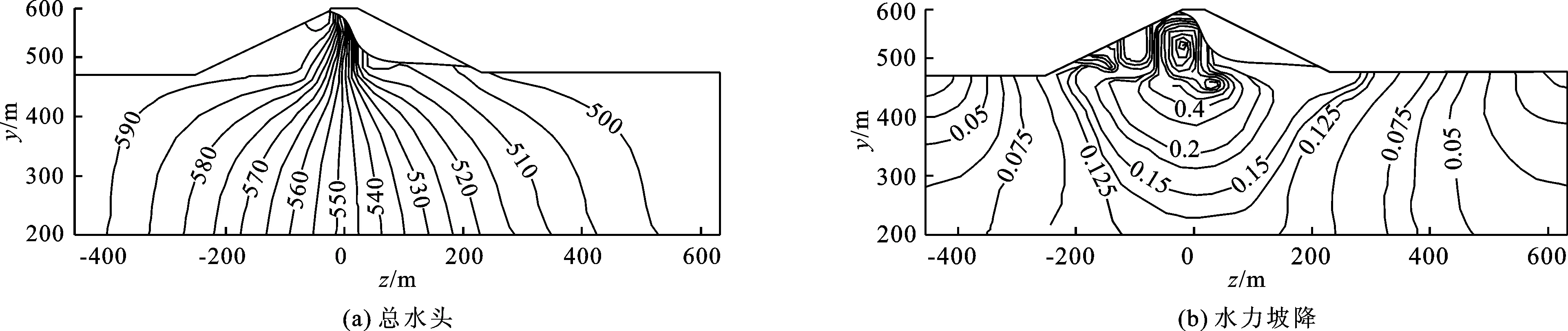
图3 x=0剖面总水头及水力坡降等值线

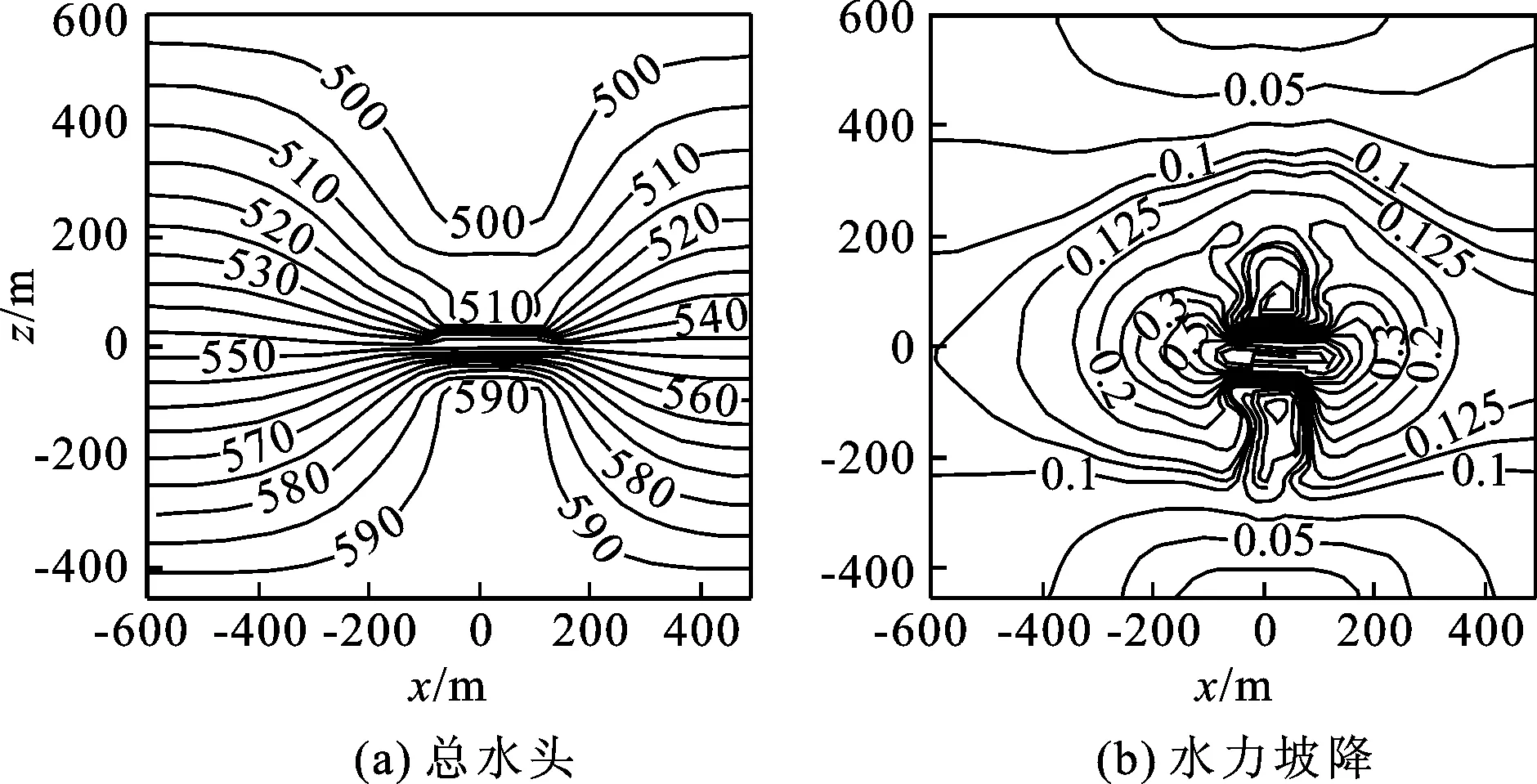
图4 y=488.5 m剖面总水头及水力坡降等值线

由图3和图4可知，水头等值线在坝体心墙部位分布较为密集，说明心墙具有较好的防渗作用。通过心墙后浸润线明显降低。坝体两岸山体产生绕过坝体向下游渗流的情况。计算所得水头等值线结果符合土石坝渗流的一般规律。在不同蓄水位上、下游水头差作用下，由于帷幕具有相对基岩较小的渗透系数，因此在帷幕上、下游侧产生相应的水头差。随着上、下游水头差的增加，不同部位帷幕上、下游侧的水头差相应增加。正常蓄水位左右两岸帷幕的最大水头差较大，约为15 m。河床中心防渗帷幕的最大水头差相对较小，约为6 m。由图5可知，沿顺河向通过心墙区域后，心墙上、下游侧水头产生明显降落。沿着坝轴线方向，心墙内部的总水头值相差较小，说明整个防渗系统沿坝轴线方向均发挥较好的防渗效果。由图5和6可知，计算所得总水头值与实测结果分布规律基本一致，正常蓄水位情况下坝体最大剖面基岩面高程处计算总水头值与实测总水头值相差2.3 m，发生在心墙上游侧的位置，其余部位计算与实测总水头值相差均小于2 m。结果表明，计算总水头值与实测结果吻合较好，说明本文采用的变分不等式方法可以用于大型土石坝枢纽工程的渗流计算。

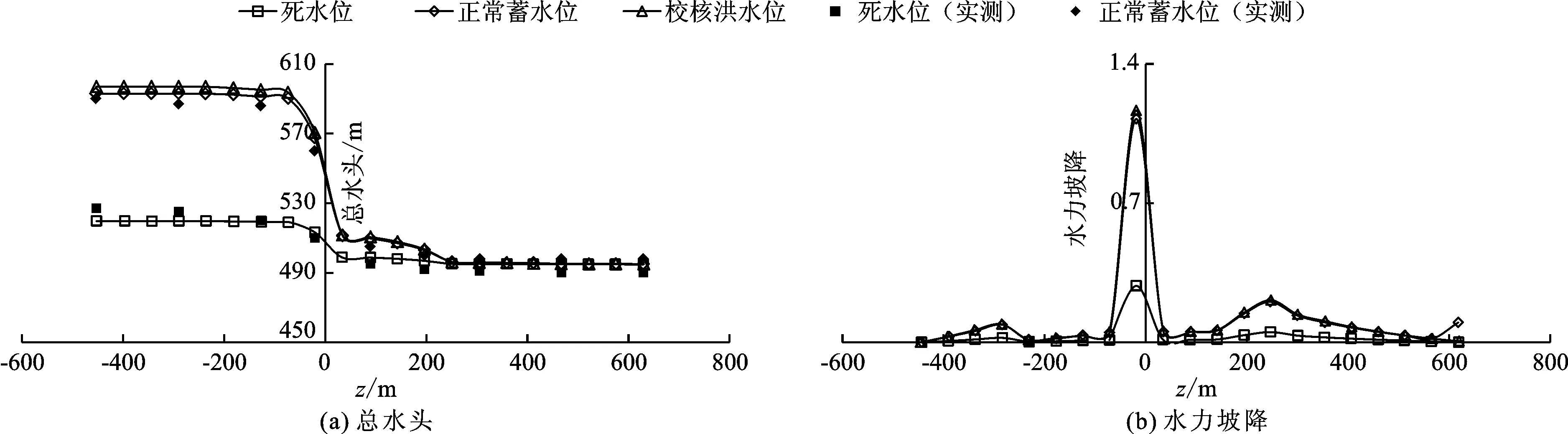
图5 不同蓄水位x=0，y=488.5m位置(坝体最大剖面基岩面高程处)总水头和水力坡降沿顺河向分布

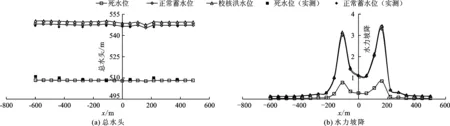
图6 不同蓄水位z=0，y=488.5m位置(坝轴线剖面基岩面高程处)总水头和水力坡降沿坝轴线方向分布

计算所得不同工况下关键部位的最大水力坡降如表2所示。与关键部位上下游水头差相对应，关键部位的水力坡降随着上游水位的增加而增加。其中死水位是水力坡降明显较小，正常蓄水位和校核洪水位相对于死水位增加明显。由图5和6可知，顺河方向心墙部位的水力坡降明显大于两侧坝壳料的水力坡降，这是由心墙上下游明显的水头差引起的。沿坝轴线方向水力坡降在大坝最大剖面附近产生明显较大的水力坡降，这是由最大剖面位置处上下游侧较大的的水头差引起的。总体而言，各部位的水力坡降均小于临界水力坡降，各岩土层满足渗透稳定要求，说明大坝整体防渗措施设置合理。不同工况下，不同部位渗流量计算结果如表3所示。随着上游水位的增加，各部位的渗流量明显增加，由于正常蓄水位与校核洪水水位的差异较小，因而两工况下各部位渗流量差异也较小。正常蓄水位工况下总渗流量为201.47 L/s，其中左岸山体的渗流量为74.53 L/s，占总渗流量的37.18%，为整个坝区的主要渗流区。原因在于左岸山体较为破碎，其渗透系数较大。左岸副坝、右岸山体、坝体以及坝基渗流量相对较小。

5.2 黏土心墙渗透性敏感性分析

本节讨论坝区渗流场对黏土心墙渗透系数的敏感性。在正常蓄水位情况下分别将黏土心墙渗透系数放大和缩小5倍进行渗流计算，分析黏土心墙渗透系数对坝区渗流场的影响。不同黏土心墙渗透系数下，x=0，y=488.5 m位置总水头和水力坡降沿顺河向变化分布如图7所示。z=0，y=488.5 m位置总水头和水力坡降沿坝轴线方向变化分布如图8所示。

图7和8表明，黏土心墙渗透系数增加时，坝体内部总水头也相应增加。这是因为黏土心墙渗透系数较小时，防渗性能较好，可以有效降低坝体内部，特别是心墙下游侧的水头值。总体而言，不同心墙渗透系数情况下，水头值相差较小，这是因为黏土心墙渗透系数的取值相差不大造成的。黏土心墙渗透系数缩小5倍时，左岸、右岸及河床帷幕部位的水头差分别增大0.46、0.09以及2.37 m，可见黏土心墙渗透系数缩小5倍，增强了心墙的防渗作用，帷幕上、下游面水头差均不同程度增大，尤其是河床中心防渗帷幕水头差增加最大。

由表2可知，黏土心墙渗透系数增加时，各关键部位的最大水力坡降均相应增加，但增加幅度整体较小，其中大坝下游坡脚处的最大水力坡降增大5.0%，相对于其他部位增加相对较大。因为黏土心墙的渗透系数很小，即使将黏土心墙渗透系数放大5倍，黏土心墙的渗透系数也相对较小，因此各关键部位的水力坡降和渗流流速变化较小。

由表3可知，黏土心墙渗透系数缩小5倍时，各部位的渗流量总体呈减小的趋势，总渗流量减小幅度为1.17%，减小幅度很小。原因是黏土心墙不是本工程的主要渗流区域，总渗流量主要受山体破碎程度、金盆左岸单薄山梁及副坝的渗透系数控制。同样将黏土心墙渗透系数增加5倍的情况下总渗流量略微增大，增大幅度只有0.57%，因为黏土心墙渗透系数放大后依然很小，且不是主要渗流区域。需要注意的是，黏土心墙渗透系数减小的情况下，左岸山体的渗流量反而会增加，这是因为坝体防渗措施较好的情况下，迫使渗透性较强的左岸山体产生较大的渗流量。

5.3 帷幕灌浆渗透性敏感性分析

在正常蓄水位情况下分别将帷幕灌浆的渗透系数放大10倍和缩小5倍进行渗流分析计算，分析帷幕渗透系数对坝区渗流场的影响。不同帷幕渗透系数对x=0，y=488.5 m位置总水头和水力坡降沿顺河向影响变化分布如图9所示；z=0，y=488.5 m位置总水头和水力坡降沿坝轴线方向变化分布如图10所示。

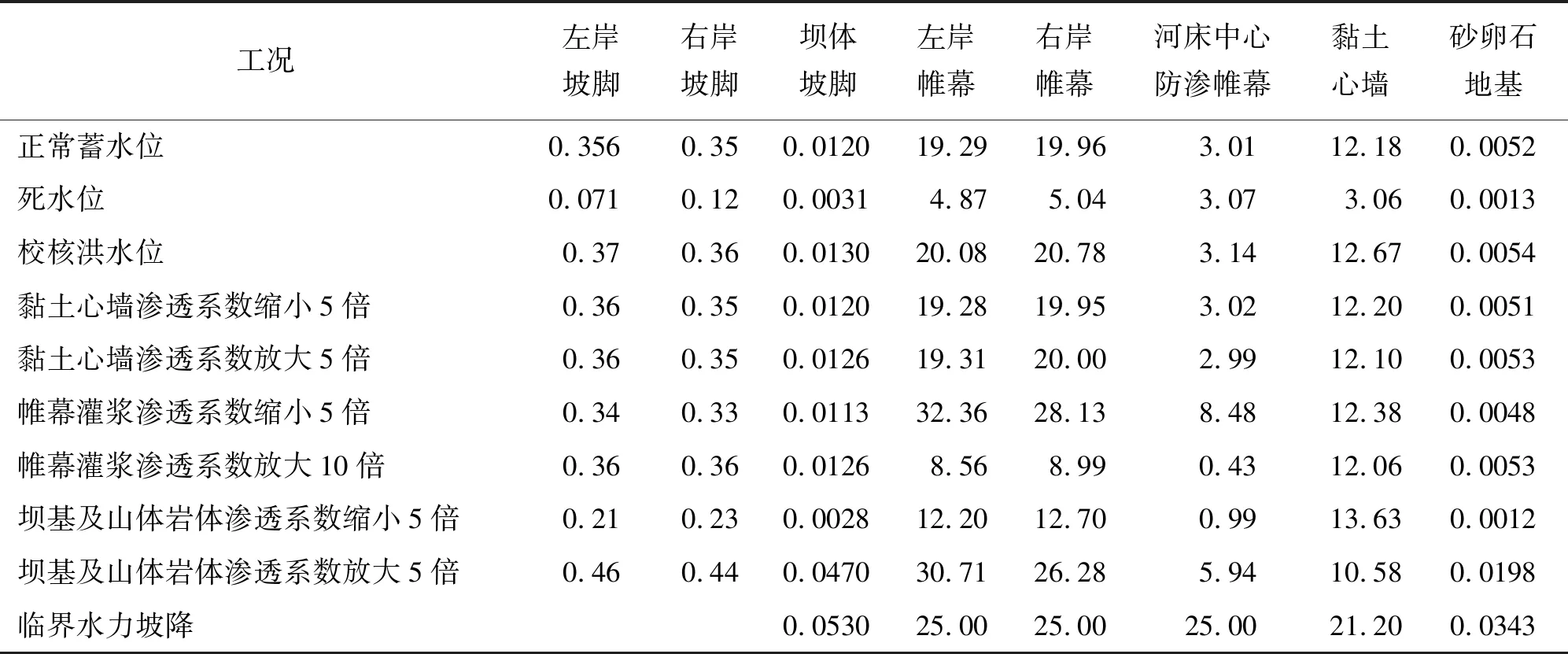
表2 不同工况关键部位最大水力坡降

图9和10表明，帷幕渗透系数减小时，坝体内部，特别是坝体下游侧总水头相应减小。帷幕灌浆渗透系数缩小5倍时，帷幕上、下游面的最大水头差均有较大幅度的增加，左岸帷幕、右岸帷幕及河床中心防渗帷幕上下游最大水头差分别增大14.03、14.28及12.58 m。由达西定律可知其水力坡降增加，说明帷幕的挡水效果有较大的增强。帷幕灌浆渗透系数放大10倍时上述关键部位水头差分别减小14.03、14.90及5.74 m，可见将帷幕渗透系数放大10倍后，帷幕上、下游最大水头差急剧减小，因为渗透系数放大后的帷幕和基岩的渗透系数相仿，即帷幕几乎没有挡水能力。

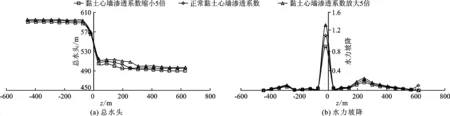
图7 不同黏土心墙渗透系数x=0，y=488.5 m位置总水头和水力坡降沿顺河向分布

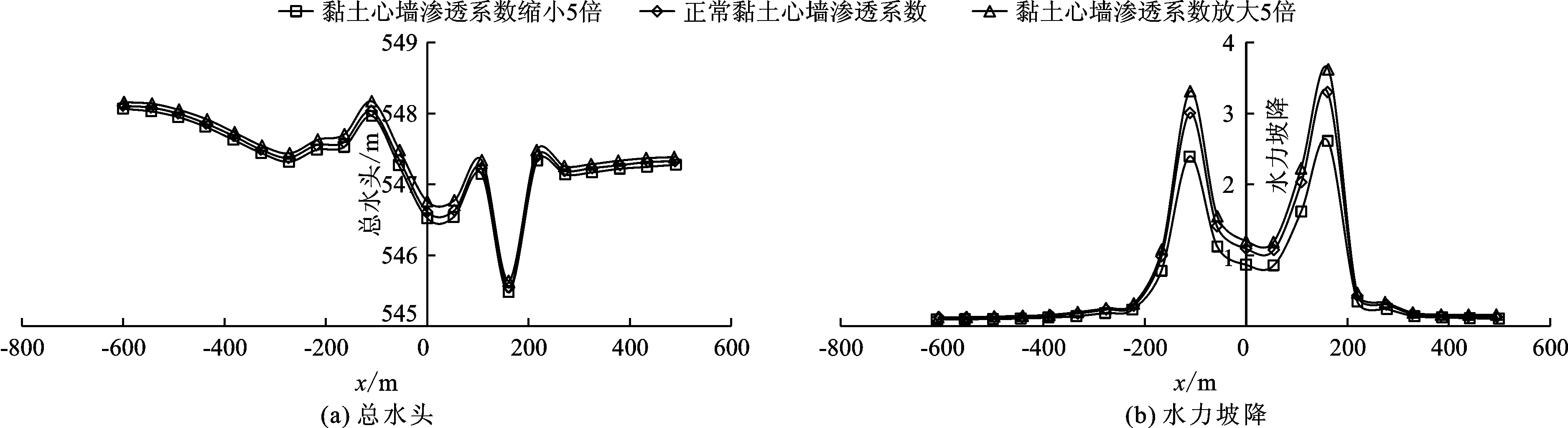
图8 不同黏土心墙渗透系数z=0，y=488.5 m位置总水头和水力坡降沿坝轴线方向分布

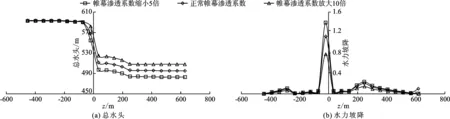
图9 不同帷幕渗透系数x=0，y=488.5 m位置总水头和水力坡降沿顺河向分布

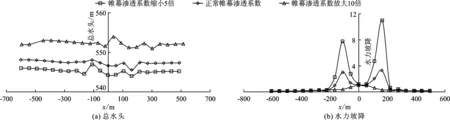
图10 不同帷幕渗透系数z=0，y=488.5 m位置总水头和水力坡降沿坝轴线方向分布

不同帷幕渗透系数情况下各关键部位水力坡降如表2所示。由表2可知，帷幕渗透系数缩小5倍时，帷幕处的水力坡降增幅较大，因为帷幕渗透系数缩小则挡水效果增强，帷幕上、下游面处的水头差增大，水力坡降提高。左右岸帷幕处的水力坡降超过允许渗透坡降25.0，因帷幕工作环境受到周围山体的约束，因此可以认为帷幕仍然处于渗透稳定状态。帷幕灌浆渗透系数放大10倍时，坝体下游坡脚和防渗帷幕的最大水力坡降具有较大的变化，其中坝体下游坡脚最大水力坡降增大5.0%，防渗帷幕的最大水力坡降减小54.96%，其中防渗帷幕的最大水力坡降减小幅度较大，因为帷幕渗透系数减小则拦水能力减弱。

由表3可知，帷幕灌浆渗透系数缩小5倍时，各部位的渗流量总体呈减小的趋势，总渗流量减小幅度为5.40%。因此将帷幕渗透系数缩小5倍在一定程度上减小了大坝下游的总渗流量，能较大程度地起到防渗作用，因为帷幕渗透系数的减小增强了自身的防渗能力，延长了上游水流的渗透路径。将帷幕渗透系数放大10倍时，总渗流量明显增加，因为帷幕渗透系数放大时，其挡水效果减弱，穿过帷幕的水流增多，即渗透路径缩短进而使渗流量增加。

5.4 坝基及山体渗透性敏感性分析

在正常蓄水位情况下分别将坝基及山体岩体渗透系数放大和缩小5倍进行渗流计算，分析坝基及山体岩体渗透系数对坝区渗流场的影响。不同坝基及山体岩体渗透系数下，x=0，y=488.5 m位置总水头和水力坡降沿顺河向变化分布如图11所示；z=0，y=488.5 m位置总水头和水力坡降沿坝轴线方向变化分布如图12所示。

图11 不同山体渗透系数x=0，y=488.5 m位置总水头和水力坡降沿顺河向分布

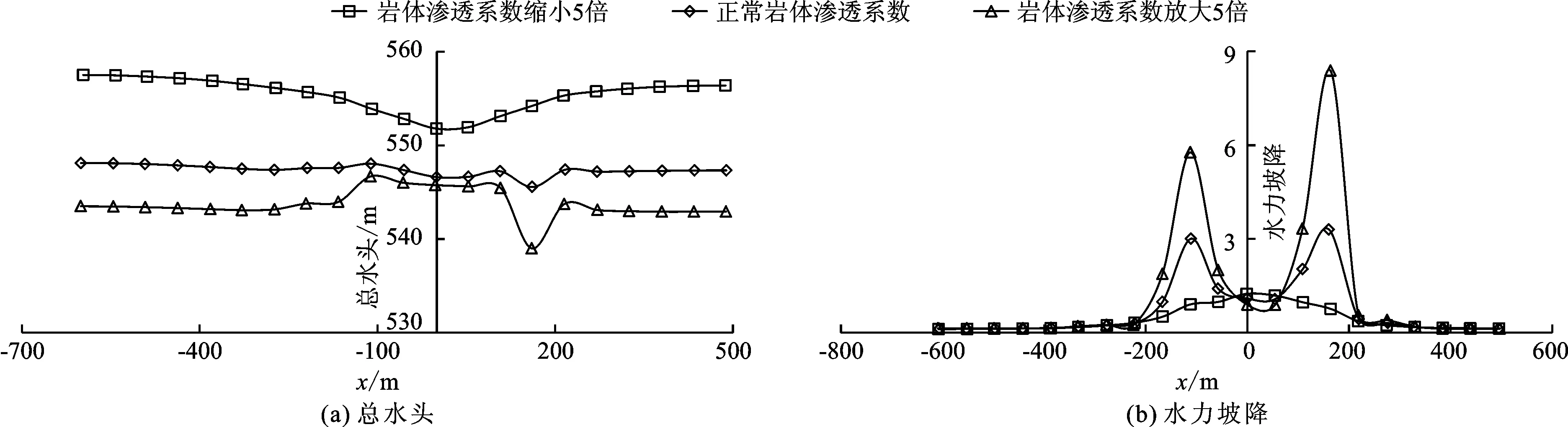
图12 不同山体渗透系数z=0，y=488.5 m位置总水头和水力坡降沿坝轴线方向分布

图11和图12表明，坝基及山体岩体渗透系数增加时，坝体内部总水头相应减小。随着坝基及山体岩体渗透系数的增加，各关键部位的最大水头差相应增加。

坝基岩土渗透系数放大5倍时，左岸帷幕、右岸帷幕及河床中心防渗帷幕上、下游面最大水头差分别增大12.96、13.87以及6.07 m。坝基及山体岩体渗透系数减小时，严重削弱了两岸防渗帷幕的防渗作用，增强了河床中心防渗帷幕的防渗作用，两岸主要是基岩阻水，河床中心主要是由心墙和帷幕阻水，因此两岸帷幕上、下游水头差很小，河床中心帷幕上、下游水头差相对较大。

不同坝基及山体岩体渗透系数情况下个关键部位水力坡降如表2所示。坝基及山体岩体渗透系数减小时，除黏土心墙外，其余各材料的最大水力坡降均有较大幅度的减小。基岩渗透系数缩小增强了其挡水能力，黏土心墙将承担更大挡水份额，因此心墙水力坡降增大；另一方面基岩渗透系数缩小，大坝上游会消耗了大部分水头，因而需大坝下游承担拦水的份额大大减小，因此帷幕、下游坝体坡脚及砂卵石料的水力坡降减小。

由表3可知，坝基及山体岩体渗透系数增大时，各部位的渗流量明显呈增加的趋势。坝基及山体岩体渗透系数缩小5倍时，计算的总渗流量减小了75.97%，坝基及山体岩体渗透系数放大5倍时，总渗流量增幅高达321.15%，说明下游总渗流量对基岩渗透系数的变化很敏感，坝基及山体岩体是主要渗流区域。

6 结 论

本文采用Signorini型变分不等式方法对黑河金盆水库坝区渗控效应进行了精细模拟。基于数值计算结果深入分析了坝区的渗控效应及渗透稳定性，研究了渗控效应对黏土心墙、帷幕、山体材料参数的敏感性。所得主要结论如下：

(1)采用Signorini型变分不等式方法获得的水头和渗流量计算结果与实测结果吻合较好，说明Signorini型变分不等式方法是精细描述土石坝枢纽渗流问题的有效方法。

(2)坝区各分区渗流量和各关键部位的最大水力坡降均在安全稳定范围内，工程渗控措施效果显著。因左、右岸岩土体较为破碎以及受左岸西北方向金盆单薄山梁和副坝的渗流场影响，坝区总渗流量主要来源于左岸山体的渗流量以及绕过帷幕的渗流量。

(3)坝区渗控效应对黏土心墙、防渗帷幕及山体材料渗透系数的变化均较为敏感，在实际工程的渗流计算中，准确把握防渗结构及山体的渗透性至关重要。