基于GA-SVR-PSO的航运安全投入优化研究

杨玉梅，张庆年，杨 杰，涂 敏，丛 喆，张 威

(1.武汉理工大学交通学院，湖北 武汉 430063；2.武汉理工大学信息工程学院，湖北 武汉 430070)

航运具有运量大、成本低、耗能少、污染小等优势，在国民经济中发挥着重要的作用。“21世纪海上丝绸之路”的提出以及建设长江黄金水道的推出，将航运业融入了国家的重大发展战略[1-2]。随着国家对航运业的重视，航运业得到了蓬勃发展，其在拉动国民经济的同时，也显露出安全事故频发的问题。2018年仅仅是长江海事局辖区内，就发生了172起航运安全事故，其中27起是船舶等级以上事故，共造成35人死亡失踪、沉船19艘，直接经济损失高达3 925.6万元[3]。因此，航运安全日渐成为航运管理者关注的重点。而航运安全与航运安全投入密切相关，航运安全投入是能够保障航运安全的必要手段，但是由于安全投入的效益是间接性的，且金融危机之后，近几年航运业的发展势态并不乐观，许多航运企业在进行安全投入决策时，考虑到成本的原因，大多尽可能地压缩安全投入，这就间接导致了航运事故率持续升高。

针对安全投入的研究，很多学者做了大量的研究，也取得了很多研究成果，但是这些研究成果主要集中在煤矿、建筑和工程建设领域。在煤炭领域中，李树刚等[4]构建了基于“人—技术—管理”的多因素煤矿安全投入评价指标体系；陈赞[5]构建了基于IPSO-SVR的绿色煤矿生产安全投入优化模型；屈奎[6]建立了基于灰色预测的煤电厂安全投入优化模型等。在建筑和工程建设领域中，王永柱[7]采用系统动力学仿真模型对建筑施工企业安全投入进行了动态分析；周建明等[8]利用李克特5分法量化了施工项目风险指数并对不同建设项目间安全投入的分配进行了研究；冯领香等[9]采用蒙特卡罗方法对Agent模型仿真得到的建设项目安全投入指标的敏感性进行了排序等。而对于航运安全投入的研究则相对较少，且大部分的研究主要集中在定性研究方面，能提出切实可行建议的定量研究较少。如陈超[10]通过费效分析提出了航运企业的安全投入产出模型，通过计算可得到航运企业成本效益最优化的安全投入费用，可为航运企业的安全管理模式和安全投入决策提供指导；邵万兵[11]利用广义DEA模型对江苏地区30家航运企业的安全投入和安全风险数据进行了分析，得出了各个航运企业的安全投入效率和安全风险分布情况，进而推动了航运企业对安全投入的重视和管理力度；容敏敏等[12]建立了航运企业安全投入的博弈模型，确定了影响航运安全投入决策的因素，并指出政府应充分发挥其监管作用;李昊[13]提出了航运系统动态安全域价值理论，并利用最小二乘法拟合了特定安全范围里的超平面，解析了航运系统安全与安全投入的关系。

综上研究可见，煤矿、建筑和工程建设领域对于安全投入的研究相对成熟，有一定的借鉴意义。为此，本文结合航运企业安全的实际情况，提出了一种基于GA-SVR-PSO的航运安全投入优化方法，构建了航运安全投入的优化模型，并通过Z航运公司2018年安全投入的实例分析，验证了该模型的可靠性和可行性。

1 相关理论

1.1 遗传算法(GA)

遗传算法(Genetic Algorithm,GA)参照了Mende的遗传学说和Darwin的进化论，是一种由模拟自然界内生物进化机理发展而来的具有随机性全局搜索及优化能力的方法。遗传算法不像传统搜索优化方法那样依赖梯度信息，而是利用编码技术，对由染色体组成的对应群体的进化过程进行模拟来寻求最优解。该算法利用选择、交叉、变异等操作产生新个体，通过选择适应度较高的个体形成新种群，建立起一个迭代过程，使种群里的个体不断地进化，并使种群渐渐接近最优，最终解决最优化计算问题。其中，选择操作，即根据个体适应度，参照一定的方法或者规则，例如联赛选择、 轮盘赌选择、Boltzmann选择等，从当前种群里选择优良个体作为父代繁殖下一代，达到选择的目的，同时体现了达尔文适者生存的思想；交叉操作，它是遗传算法里重要的操作之一，通过交叉操作能产生组合父辈特性的新个体，以某个交叉概率交换群体内搭配成对的个体之间的部分染色体，即进行部分信息交换，则能得到互换信息后的新个体，常用的交叉操作的方法主要有点交叉、多点交叉和均匀交叉等；变异操作，即通过变异概率来改变种群中的个体里某一个或某些基因座上面的基因值为其他等位基因，从而产生新个体。

1.2 支持向量回归(SVR)模型

支持向量机(Support Vector Machine,SVM)是Vapnik[14]在1995年提出的以统计学习理论为基础的多方面应用的一种新方法。SVM借助最优化理论，能成功地解决模式识别问题(SVC)和回归问题(SVR)等，是数据挖掘中能推广到综合评价和预测领域的一种新技术[15-20]。本文应用支持向量回归(SVR)模型模拟航运安全投入与经济损失之间的定量关系。

SVR模型将输入的自变量指标x1,x2,…,xm映射至高维特征空间[φ(x1),φ(x2),…,φ(xm)]中，能将原始非线性模型转化为特征空间里的线性模型，即:

f(xi)=ωTφ(xi)+B

(1)

式中：xi为样本点;φ(xi)为非线性映射;f(xi)为特征空间中的线性函数；ω为待辨识的权重；B为常数项。

根据结构风险极小化和SVR原则，对该回归模型中待辨识的权重ω和常数项B进行处理，得到SVR模型的优化函数：

(2)

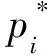
从而得到SVR模型的决策函数：

(3)

K(xi,x)=exp(-g‖xi-x‖2)

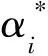
1.3 交叉验证

交叉验证(Cross Validation,CV)是一种应用于验证分类器性能的统计分析方法，其基本思想是将原始数据在某限制下划分组别，一部分当成训练集，另一部分当成验证集，先将训练集输入模型训练模型，再将验证集输入训练好的模型进行测试，并以此作为评价性能指标。常见的CV方法有Hold-Out Method、K-fold Cross Validation(K-CV)和Leave-One-Out Cross Validation(LOO-CV)三类。CV方法能保证模型的可靠性和稳定性，因此本文选取K-CV方法进行交叉验证，将原始数据均分为K组，用每个子集分别做一次验证集，剩余的K-1组子集当成训练集，结果生成K个模型，将K个模型最终验证结果的平均数作为该K-CV方法的性能指标。

1.4 粒子群优化算法(PSO)

粒子群优化算法(Particle Swarm Optimization,PSO)源于对鸟群觅食全过程的模拟，被Kennedy等[21]于1995年开始用于优化计算，大量的实践证明PSO是很好的优化算法[22-29]。PSO算法基于群体的概念而产生，一系列个体粒子组成粒子群，个体粒子在自变量定义域确定的搜索空间中进行运动，在搜寻最优解的过程中，飞行经验会对粒子的飞行速度进行即时动态调整，见公式(4)，每一个粒子的位置代表着每一个可能解，见公式(5)：

(4)

(5)

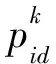
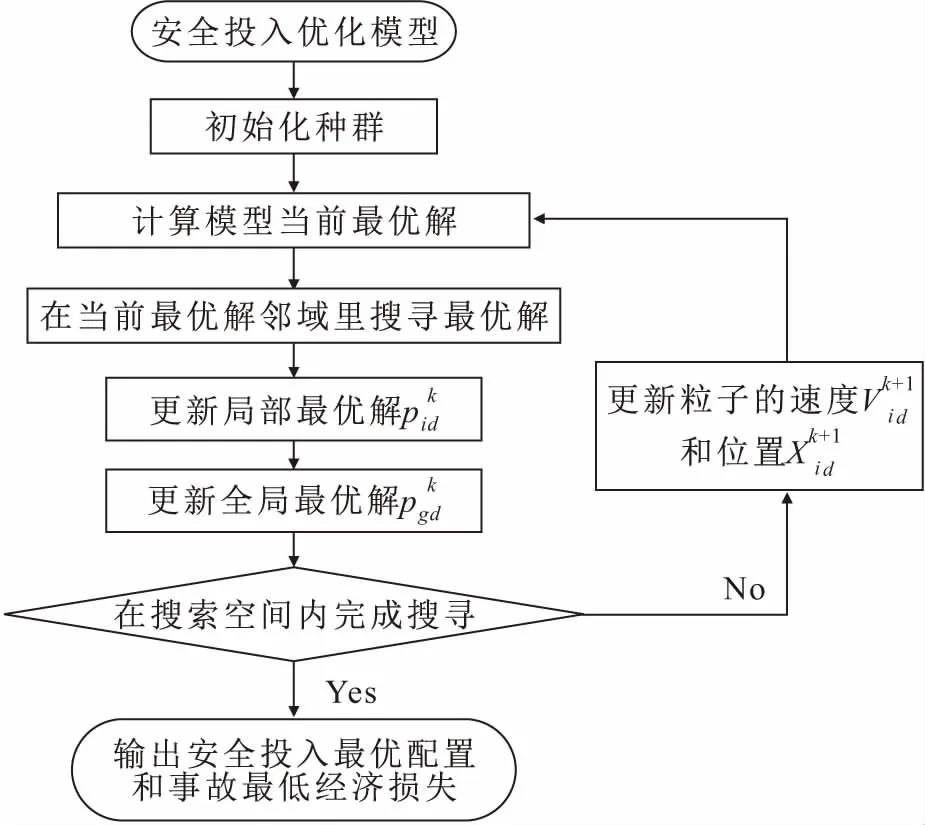
图1 PSO算法流程图Fig.1 PSO algorithm flow chart

2 GA-SVR模型的构建

SVR模型的预测精度受参数c、g、p的影响较大，惩罚因子参数c设置太大或太小都会引起模型过学习或者欠学习，核函数参数g也会间接地影响模型构建分类器空间的性质，不敏感损失系数p对模型支持向量的数目和预测精度也有影响。GA算法具有全局搜索和速度快的优点，而K-CV方法能有效地避免欠学习和过学习状态，因此将两者结合能较好地优化SVR模型的参数。因此，本文采用GA和K-CV结合的方式对SVR模型的参数进行优化。GA-SVR模型的构建流程见图2。

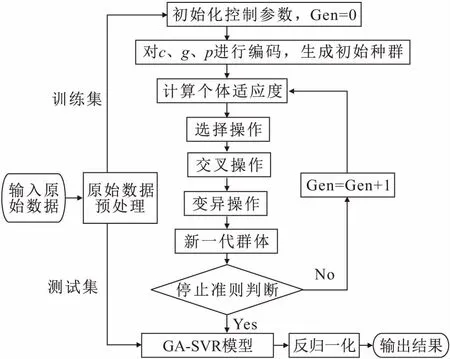
图2 GA-SVR模型的构建流程图Fig.2 Construction flowchart of GA-SVR model注：Gen为迭代次数

3 某航运公司安全投入的预测与优化

3.1 GA-SVR模型训练与验证

3.1.1 某航运公司安全投入指标原始数据

影响航运安全的因素很多，但是实际上航运企业能通过安全投入改善安全状态的因素主要集中在“人—机—管理”这一系统里。本文结合“人—机—管理”系统工程理论和实际调研情况，将2001—2018年Z航运公司安全投入指标和当期航运事故造成的经济损失原始数据列出，见表1。

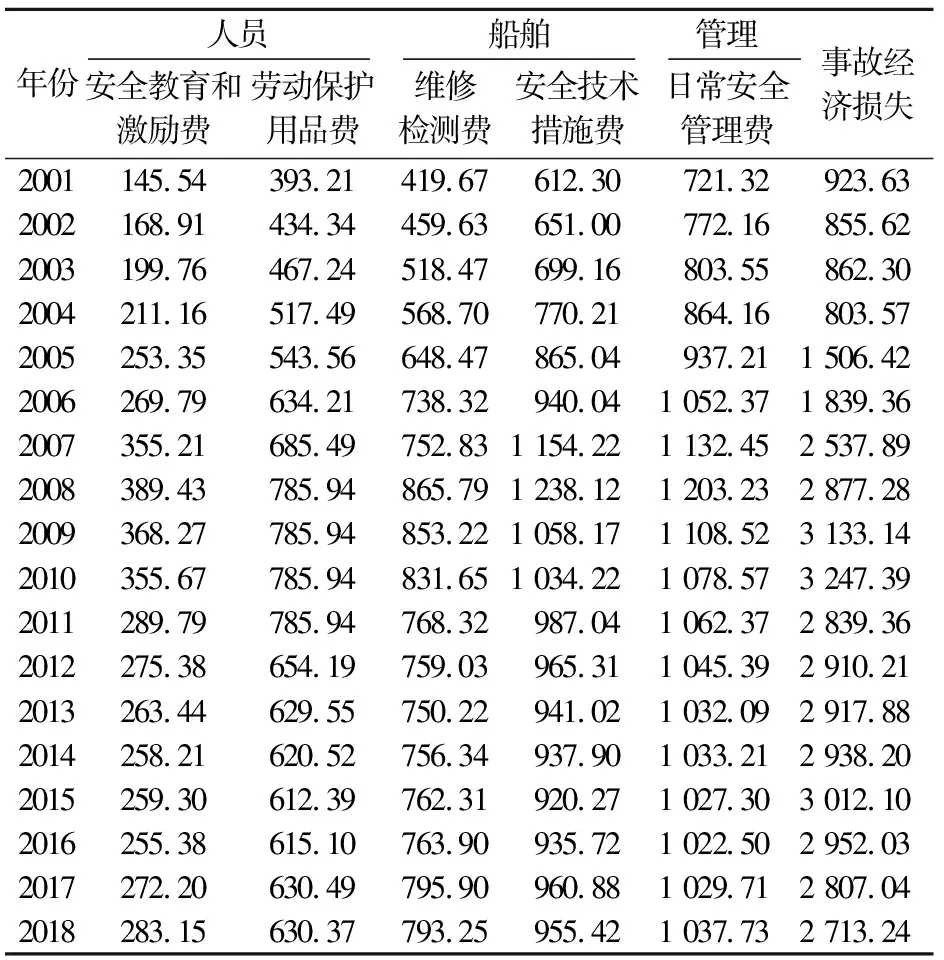
表1 2001—2018年Z航运公司安全投入指标和航运事故经济损失原始数据表(单位：万元)

由表1可知，随着航运业的发展，航运量不断增加，Z航运公司不断扩大规模，因此安全投入费用也相应增加；但是在2008年金融危机之前的鼎盛期，Z航运公司的安全投入已跟不上公司规模扩大后航运安全的需要，导致航运事故经济损失出现高升状态，2008年经融危机之后，航运业一直处于低迷状态，Z航运公司在已扩大的规模上进行相应的安全投入已经有点力不从心，因此航运事故经济损失仍保持在较高的水平。

3.1.2 原始数据预处理

为了方便模型训练以及数据统一化，本文采用最大最小化方法对原始数据进行归一化处理，将原始数据控制在[0,1]范围内。原始数据具体的归一化处理公式如下：

(6)

3.1.3 模型参数的初始设置

交叉验证采取5折验证的方式，将原始数据均分为5组，用每一个子集分别做一次验证集，剩余的4组子集当成训练集。GA算法中的进化代数设为250，种群数量根据经验应为变量数目的4～6倍[31]，即为20～30个，本文采用试凑法确定其为30个。c、g、p参数的初始范围分别设置为[0,100]、[0,100]、[0,1]。

3.1.4 模型训练与验证

本文采用2001—2015年Z航运公司安全投入指标数据作为训练集，其中将“人员—船舶—管理”涉及的[安全教育和激励费、劳动保护用品费]、[维修检测费、安全技术措施费]和日常安全管理费这五个安全投入指标数据作为GA-SVR模型的输入指标，以航运事故经济损失作为输出指标，并采用2016—2018年Z航运公司安全投入指标数据作为测试集验证模型训练的效果。GA算法对SVR模型参数进行寻优过程中，种群适应度函数曲线见图3，最终搜寻到的最优参数为c=14.631 7、g=0.396 54、p=0.033 287。

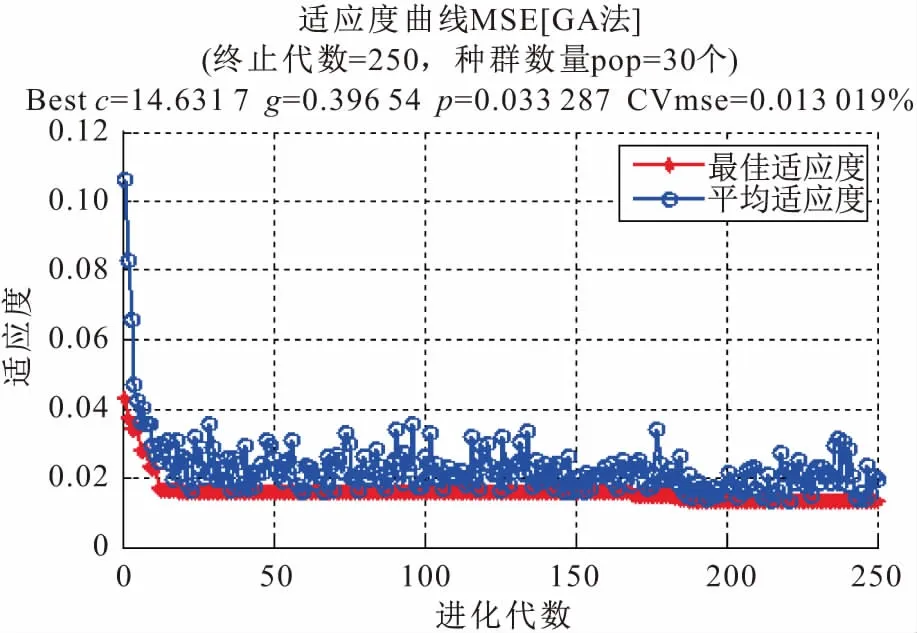
图3 种群适应度函数曲线Fig.3 Population adaptation function curves

将最优参数输入SVR模型对训练集数据进行训练，得到训练好的SVR模型，模型中训练集和预测集的拟合曲线见图4。训练集预测的均方误差MSE为0.01，相关系数为0.91，其拟合效果较好。

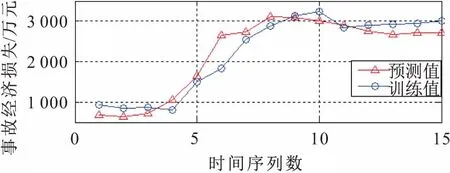
图4 训练集的拟合效果图Fig.4 Fitting effect diagram of the training set

将测试集数据代入训练好的GA-SVR模型中验证模型预测的精度，模型中测试集和预测集的拟合曲线见图5。测试集预测的MSE为0.005，其预测精度较高。

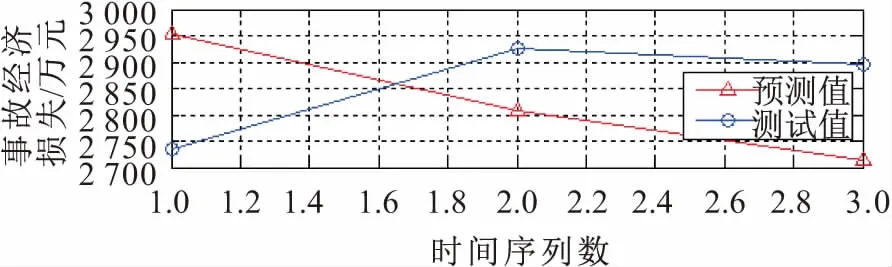
图5 测试集的拟合效果图Fig.5 Fitting effect diagram of the test set

经过模型训练与验证，说明构建的GA-SVR模型能很好地表达出Z航运公司安全投入与事故经济损失之间的定量关系，可为后续该公司航运安全投入优化研究奠定基础。其定量关系表达式如下：

(7)

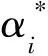
3.2 基于PSO算法的航运安全投入优化

3.2.1 航运安全投入优化目标与约束条件

本文以Z航运公司2018年安全投入为例进行航运安全投入优化研究。Z航运公司2018年安全投入总费用约为4 000万元，安全投入优化目标是在2018年总安全投入费用4 000万元以及分项投入约束条件下当期航运事故经济损失最小。根据相关规定和Z航运公司安全决策限制，为了防止安全投入在每一个投入分项里投入不足或者过高，对每一个投入分项设置投入上、下限，Z航运公司安全投入的优化决策表达式如下：

目标函数为

(8)

目标约束为

(9)

3.2.2 基于PSO算法的安全投入优化计算

由于决策函数是高维空间的线性函数，用一般的寻优算法难以进行寻优，因此本文采用自适应权重PSO算法对目标函数最小值进行搜索，PSO算法参数的初始设置见表2。

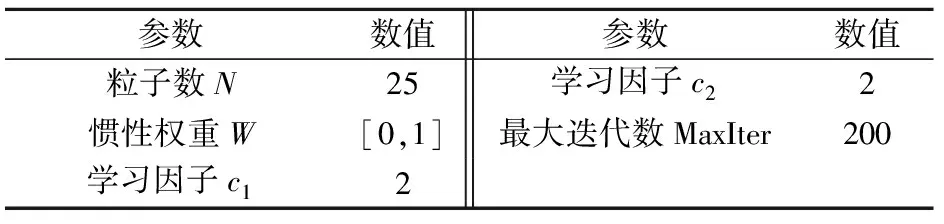
表2 PSO算法参数的初始设置

通过PSO算法编程计算，经过约8.5 s，计算得到该航运公司航运事故经济损失最小值为1 979.96万元，比2018年该公司航运事故实际经济损失降低了733.28万元，此时最优的安全投入组合为x=[507.51,430.41,434.52,1 146.74,1 153.39]，合计总安全投入费用约为3 700万元。

将计算结果与实际情况进行对比可知，本文建立的航运安全投入-事故经济损失关系模型与航运安全投入优化模型能够很好地结合，可为航运企业安全投入决策提供依据。

4 结论与建议

本文验证了通过GA-SVR模型构建的航运安全投入与事故经济损失定量关系模型的有效性和可靠性，并结合实际决策限制，利用PSO算法对航运安全投入优化模型进行了优化，最后以Z航运公司2018年安全投入为实例，验证了基于GA-SVR-PSO的航运安全投入优化方法的可靠性，经安全投入优化组合后预计能降低733.28万元的航运事故经济损失。该方法可为航运企业安全投入决策提供可靠的依据，从而提高航运安全投入效率，减少事故经济损失。

本文在模型构建时，由于样本数量有限，并受到实际安全投入财务资料的限制，模型参数设置受到随机因素的影响。但该方法若能应用于多家航运企业，并能采用更长年份的历史数据，则可进一步提高模型的预测精度，从而提高其实际应用价值。