基于汉堡车辙试验的沥青路面永久变形预估模型研究
2020-04-20曹荣吉吴春颖
李 锋,曹荣吉,吴春颖,刘 伟
(1.苏交科集团股份有限公司,江苏 南京 211112; 2.新型道路材料国家工程实验室,江苏 南京 211112)
0 引 言
车辙是沥青路面的主要病害之一,车辙深度的发展趋势对于养护决策和未来养护规划具有重要意义,因此,车辙深度预估模型也成为了国内外沥青路面技术研究的热点。总体而言,沥青路面车辙深度的预估方法主要包括经验法、力学-经验法和力学理论分析法。经验法缺乏对车辙开展机理分析的理论基础,难以对不同结构、不同材料和不同环境的路面永久变形做出准确估计,结论不具有普适性,难以进行大规模的推广。力学理论分析法理论相对比较完善,且耗资少,但全面反映沥青混合料在重复荷载作用下永久变形的本构理论和试验测定方法还不成熟,有待进一步深入研究。力学-经验法在经验法的基础上引入力学参数, 实现了路面结构-材料一体化设计,是目前沥青路面设计的主流方法[1-3]。中国也借鉴了AASHTO 2002中的MEPDG力学经验设计方法[4-5],形成了适用于半刚性基层的沥青路面力学经验设计方法。其中,在沥青路面永久变形预估模型中,按照弹性层状体系,将沥青路面面层分为不同的亚层,按照各层的永久变形进行累加,模型中考虑温度、荷载、荷载作用次数以及厚度等影响因素。
然而,现行规范中的车辙预估模型主要基于国产车辙板试验而来,标准试件尺寸为长300 mm、宽300 mm、高50 mm,对于既有路面而言,各层厚度不同,尤其上面层一般仅有40 mm,难以满足车辙板试件尺寸要求,方形试件取样也较难。因此,对于养护工程,通过车辙板试验评估老路面材料的高温稳定性,进而采用基于车辙板试验的车辙模型预估养护后路面的车辙深度发展趋势已较难实现。汉堡车辙试验可通过钻芯取样的方式开展老路面材料的高温稳定性评价,取样方式简单,试件直径为150 mm,厚度为38~100 mm[6]。因此,本文的主要目的是通过汉堡车辙试验建立车辙深度预估模型,为路面养护和规划提供决策依据。
1 国标和汉堡车辙试验相关性分析
为了建立国标车辙试验和汉堡车辙试验之间的相关性,在室内成型4种沥青混合料,分别开展国产车辙试验和汉堡车辙试验,其中国产车辙采用长300 mm、宽300 mm、高50 mm的方形车辙板试件,汉堡车辙采用旋转压实成型后钻取直径为150 mm、高度为60 mm的圆柱体试件,试验条件均为60 ℃、0.7 MPa,3种沥青混合料分别为改性沥青SMA-13、改性沥青AC-13和普通沥青SUP-25[7-8]。SMA、AC类混合料采用马歇尔设计方法,SUP类混合料采用Superpave设计方法,最终确定的沥青混合料材料组成和合成级配分别如表1、2所示。在最佳油石比下,沥青混合料的最佳油石比与马歇尔试件的体积参数如表3所示,各项指标满足现行规范的技术要求,混合料性能验证均满足要求。车辙试验结果如图1所示。

表1 材料组成

表2 合成级配

表3 混合料体积参数
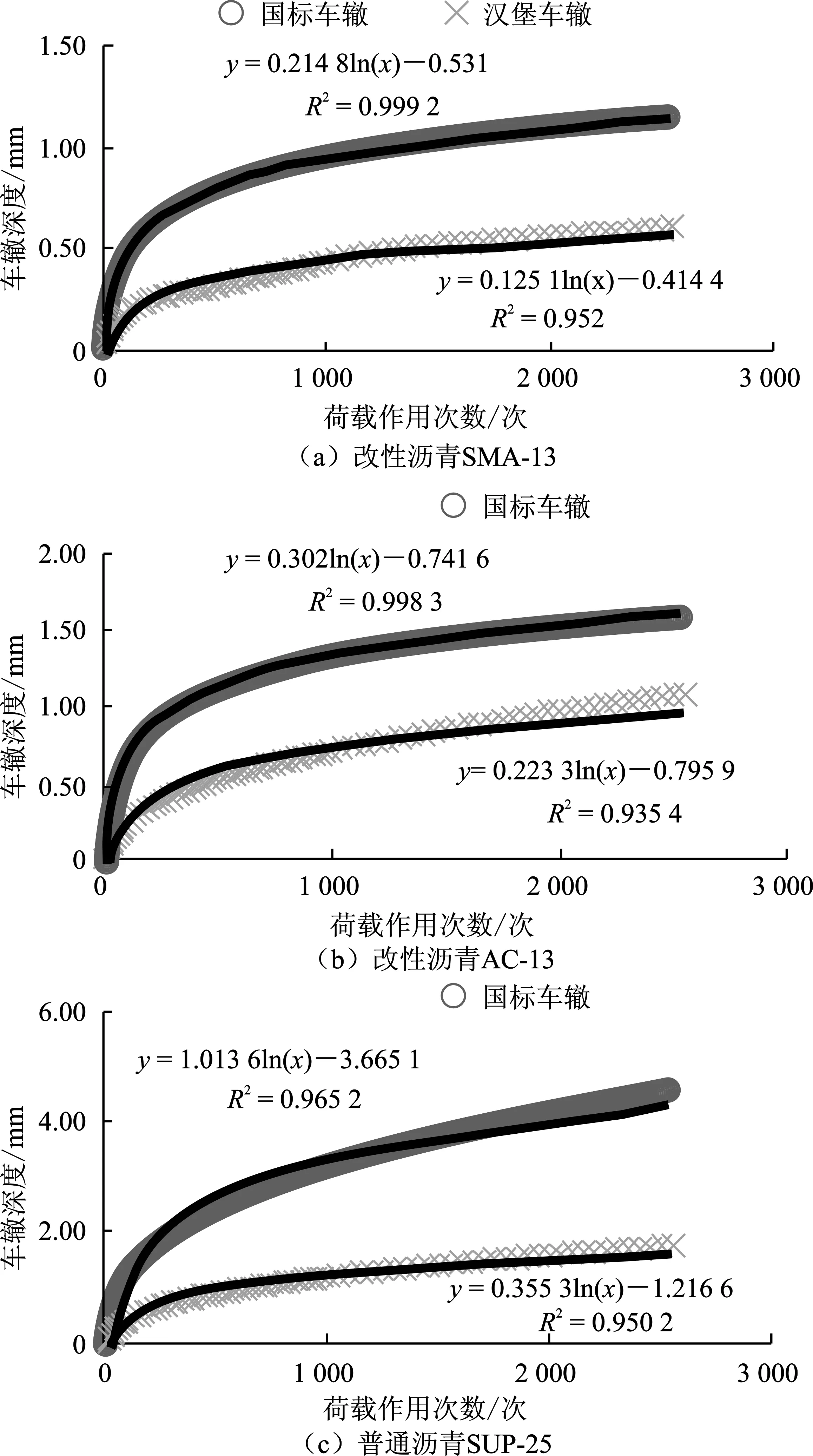
图1 车辙深度试验结果
结果表明,车辙深度与荷载作用次数之间存在很好的相关性,对于改性沥青混合料和普通沥青混合料,汉堡车辙深度和国标车辙深度之间存在一定的差异,普通沥青混合料的差异相对较大。在相同的荷载作用次数下,国标车辙深度明显大于汉堡车辙深度。
基于改性沥青SMA-13和AC-13沥青混合料的国标车辙和汉堡车辙试验结果,通过回归分析得到两者之间存在很好的线性相关性,判定系数R2为0.94,如图2所示。基于对数回归得到的普通沥青SUP-25沥青混合料车辙深度与荷载作用次数之间的关系,可推出普通沥青混合料国标车辙和汉堡车辙之间的关系。最终的关系式分别如式(1)、(2)所示。
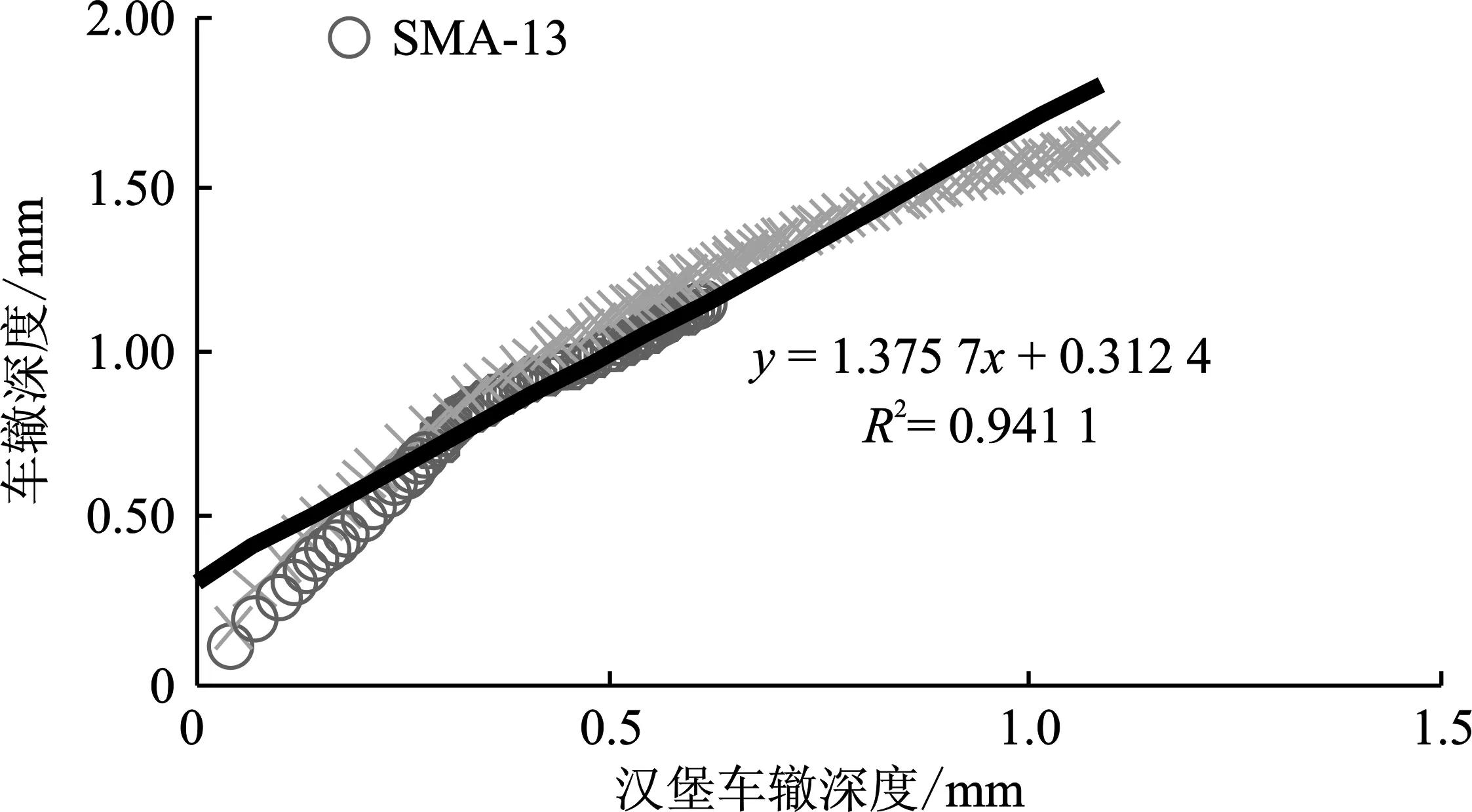
图2 国标车辙与汉堡车辙的相关性
对于改性沥青混合料
RGB=1.38RHB+0.312
(1)
式中:RGB为国标车辙深度(mm);RHB为汉堡车辙深度(mm)。
对于普通沥青混合料
RGB=2.85RHB-0.195
(2)
2 室内车辙试验
2.1 汉堡车辙试验
在某高速公路进行取芯,路面结构为4 cm改性沥青SMA-13+6 cm改性沥青AC-20+8 cm改性沥青AC-25,芯样直径为150 mm。分别针对上、中、下面层材料进行切割,然后开展室内汉堡车辙试验,试验方案考虑了温度、荷载大小和荷载作用次数3个因素。根据交通荷载状况,选择的试验轮胎荷载包括标准接触应力700 N,超载应力800 N和900 N,试验温度由低到高依次为50 ℃、60 ℃和70 ℃。分别记录每隔2 000次荷载作用的车辙变形深度,试验结果如图3所示。
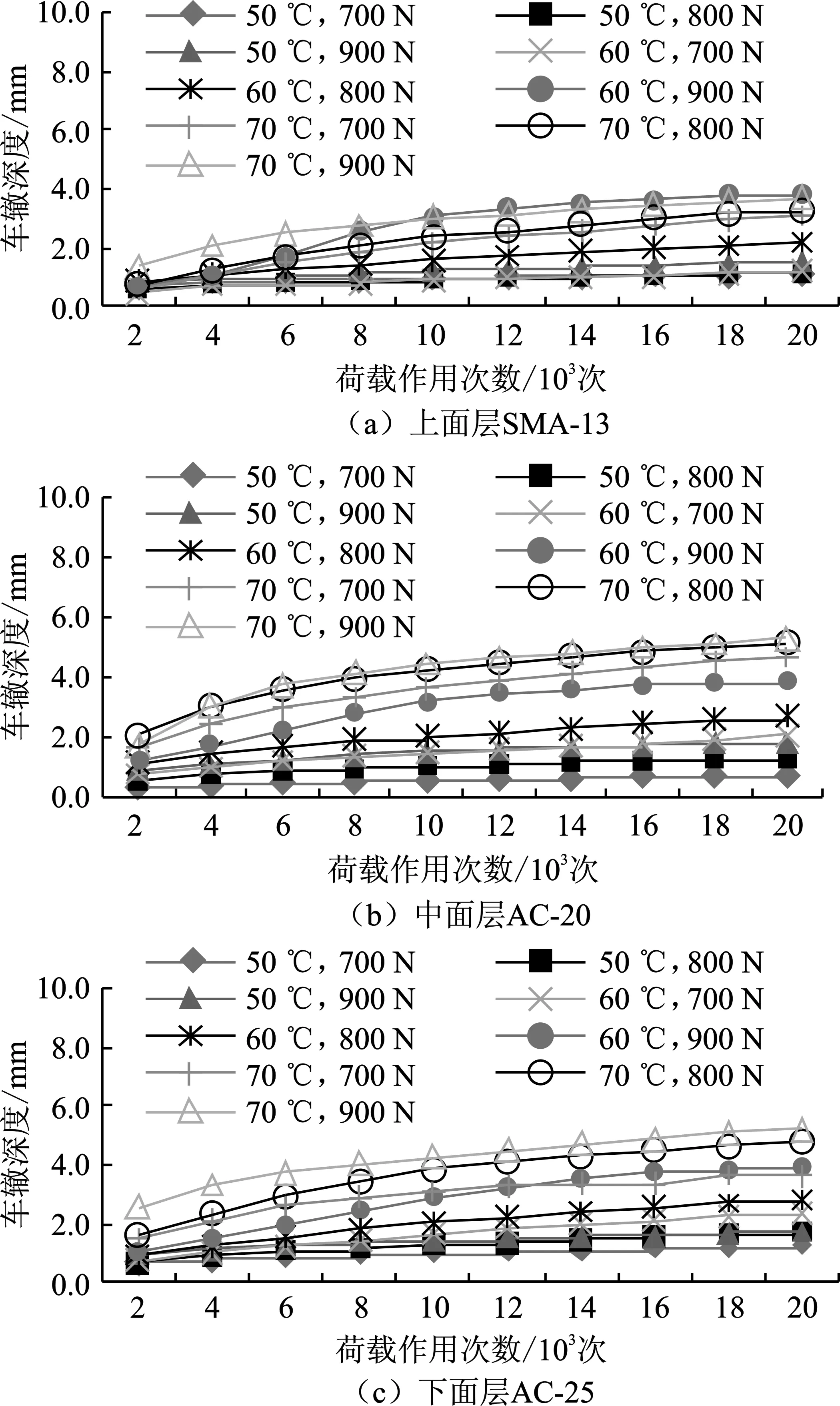
图3 车辙发展趋势
2.2 国标车辙试验
为了扩充样本数据,提升回归模型的可靠性,在此引用同济大学《沥青混合料和沥青面层抗永久变形预估》研究报告中的国标车辙试验数据[9],通过前文研究得到的汉堡车辙深度与国标车辙深度之间的关系,将国标车辙试验数据转换为汉堡车辙数据,然后与本项目中的汉堡车辙试验数据共同回归分析,得到车辙深度室内模型。引用的国标车辙数据包括普通沥青混合料AC-20,以及改性沥青混合料AC-13、AC-20和SMA-13。根据前文得到的回归方程转换得到的汉堡车辙试验数据,如表4所示。
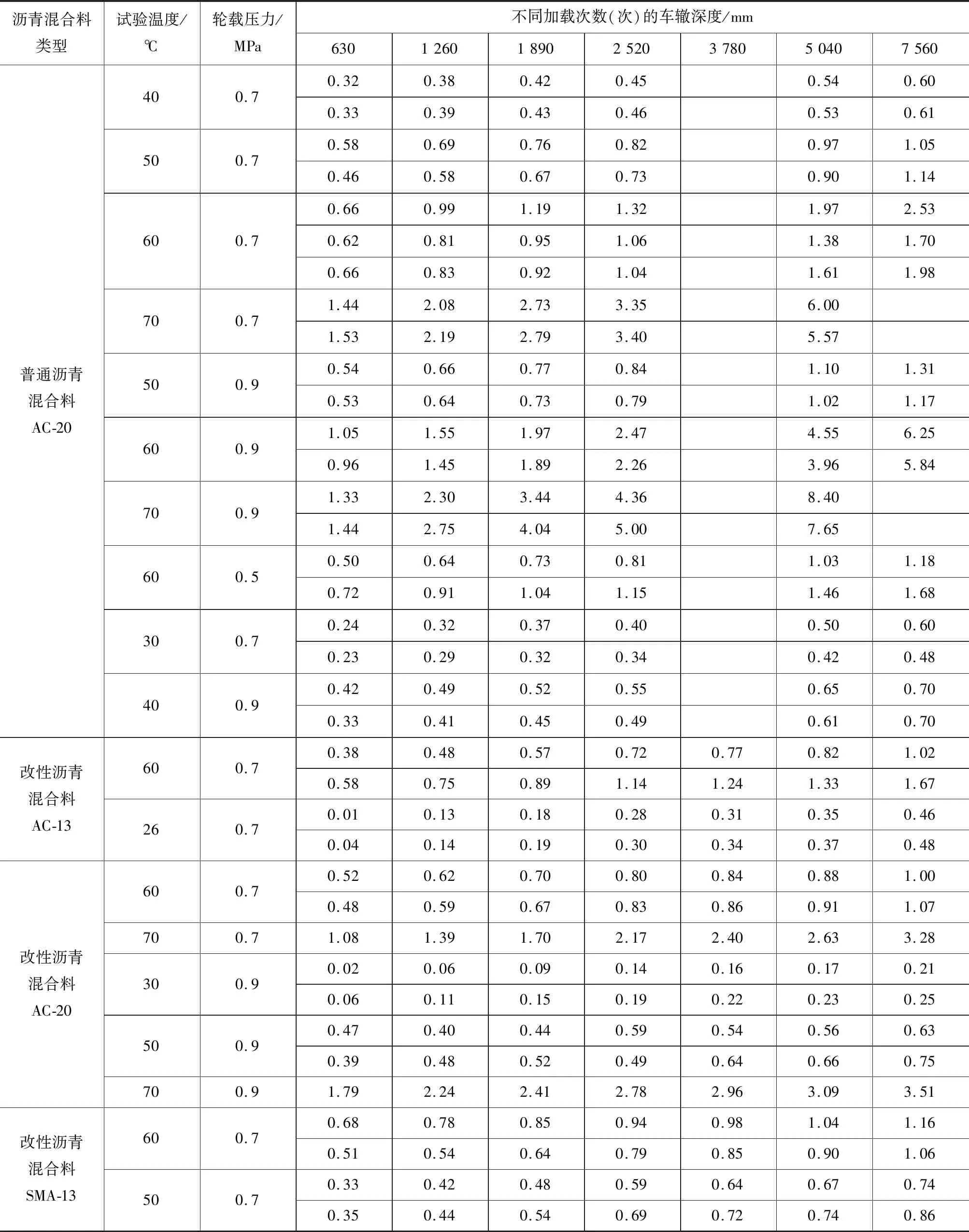
表4 国标车辙数据转换成汉堡车辙数据结果
3 室内车辙深度模型
3.1 建立室内车辙模型
采用车辙深度因子R0表征沥青混合料的车辙深度性能,并作为惟一的反映材料高温稳定性参数的材料因子。原路面材料R0可通过汉堡车辙试验得到,养护材料的R0可进行国标车辙试验,并通过与汉堡车辙之间的关系转换。影响R0的因素很多,重点考虑了轴载累计作用次数N、作用压力P以及试验温度T三个主要环境因素。由于室内试验采用的试件厚度与实际路面厚度不同,为了消除厚度对预估模型的影响,引入了层次厚度参数d,通过固定的室内试件厚度,推求其他厚度下的车辙深度。
通过对沥青混合料车辙深度基本模型的调研,确定采用Shami建立的沥青混合料车辙深度预估模型R=f(R0,T,N)为基本形式,建立车辙深度R与温度T、荷载P、作用次数N等因素之间的关系。针对各个因素的不同水平,分别采用预估因子T/T0,P/P0,N/N0,将各个因素等效换算至标准条件。同时,考虑原路面各分层厚度不同,引入厚度因子d/d0(d0为初始厚度)。由此得出考虑温度、荷载、作用次数和厚度因素,沥青混合料车辙深度预估模型的初步形式为
(3)
式中:t、p、n为回归参数;k为修正系数;R0,T0,P0,N0为标准条件下的测试结果。
标准车辙试验的条件为:P0=0.7 MPa,T0=60 ℃,N0=20 000次,d0=60 mm。以标准试验条件下的汉堡车辙试验为基准,将其他试验条件下的车辙深度R除以标准试验条件下的车辙深度R0,以其他试验条件分别除以基准条件,得到数据组:R/R0、T/T0、P/P0、N/N0、d/d0,对该数据组中的每个数据取对数。采用Excel数据分析功能,以lg(R/R0)作为因变量,以lg(T/T0)、lg(P/P0)、lg(N/N0)和lg(d/d0)作为自变量,对270组数据组进行多元回归分析,可以得到车辙深度的室内模型的各项回归指数。对本项目研究得到的270组汉堡车辙试验数据,以及通过相关关系将国标车辙转换成的207组汉堡车辙试验数据,进行多元回归,结果如式(4)所示。
R=5.91×10-6T1.921P0.405N0.333d0.249R0
(4)
回归分析结果表明,车辙深度与各项参数之间的相关性达到了0.906,判定系数R2为0.821,具有很好的相关性。各项参数中,厚度d、温度T、荷载P、作用次数N对车辙深度R的P-value均远远小于0.05,具有很好的相关性,且P-value大小依次为:d>P>T>N,表明在车辙深度各影响因素中,荷载作用次数最显著,温度次之,厚度显著性相对较差。
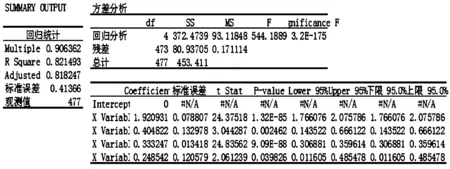
图4 统计分析结果
3.2 验证室内车辙模型
为评价室内车辙深度预估模型的预测精度,选取不同路段的旧路面材料和新成型的养护材料开展汉堡车辙试验,实测不同类型材料的实际车辙变形量Rr,与车辙预测模型得到的计算值Re进行对比,通过相对偏差等指标计算,以相对偏差小于20%验证室内车辙深度预估模型的可靠性。分别对8条在役高速公路共38个断面进行了取芯,开展中、下面层混合料的汉堡车辙试验,得到共计414组车辙深度实测数据,计算各类材料的车辙深度,并计算相对偏差,结果如表5所示。分析结果表明,在20组数据中,共有18组数据的相对偏差小于20%,平均相对偏差为14.8%,可见建立的室内车辙模型满足预测精度。根据图5中的实测值与预估值的相关性可知,模型的精度相对较高,判定系数R2达到了0.917 6。
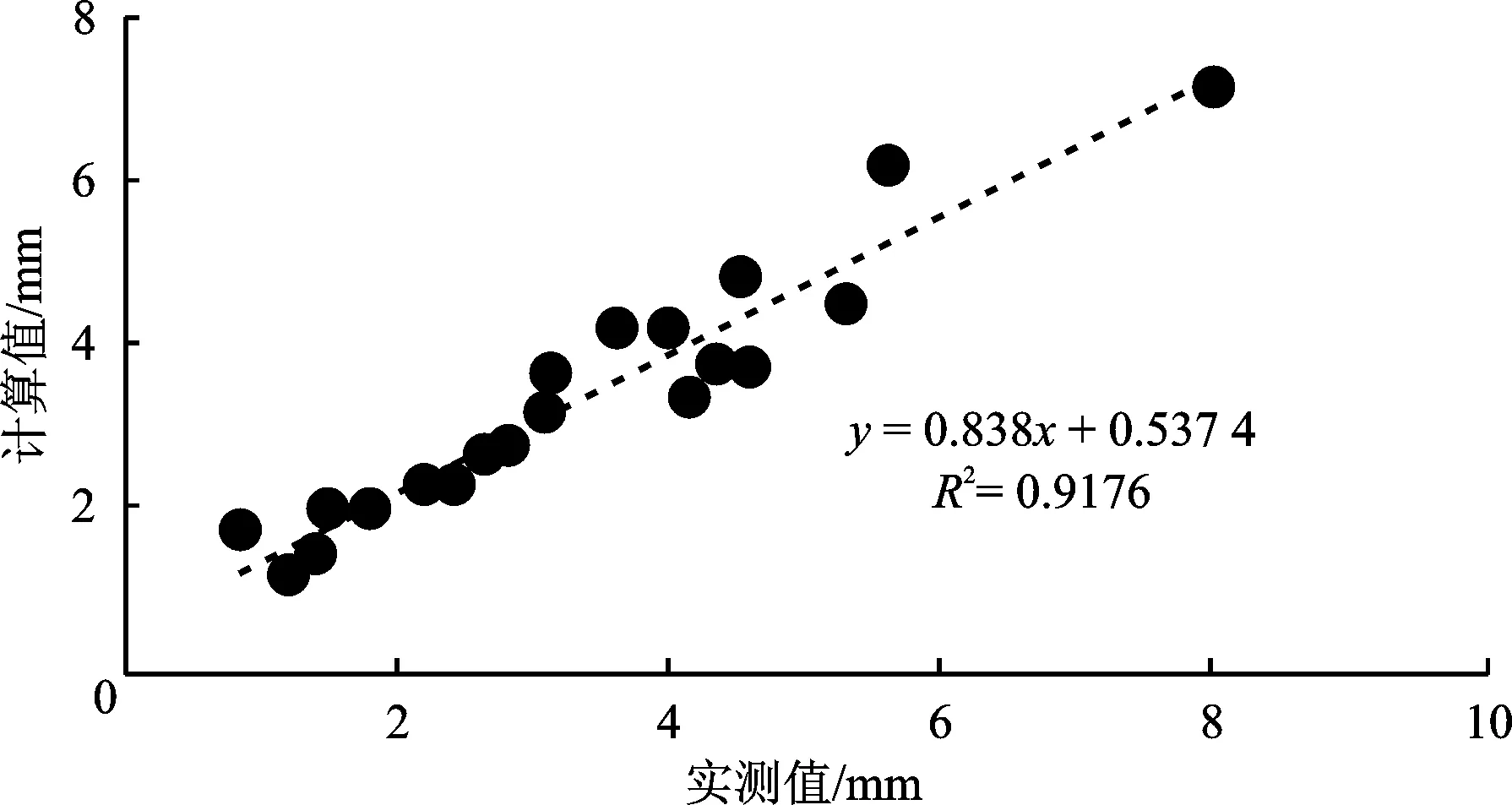
图5 实测值与计算值的相关性

表5 室内车辙模型验证结果
4 结 语
(1)基于室内成型新沥青混合料试件,开展了国标车辙试验和汉堡车辙试验相关性分析,分别建立了改性沥青混合料和普通沥青混合料汉堡车辙深度与国标车辙深度之间的关系,二者之间存在较好的相关性,在同样条件下,国标车辙试验结果大于汉堡车辙试验。
(2)基于既有路面芯样,分别针对上、中、下面层开展不同温度、荷载和荷载作用次数条件下的汉堡车辙深度试验,并结合已有国标车辙试验数据,通过二者之间的相关关系转换为汉堡车辙深度数据,共得到477组数据,通过多元回归建立了基于汉堡车辙试验的车辙深度室内模型。
(3)通过对8条高速公路38个断面进行取芯,分别开展各芯样中面层和下面层汉堡车辙试验,得到共计414组车辙深度实测数据,并结合已有文献中的车辙深度试验数据,对建立的室内车辙模型进行验证,平均相对偏差为14.8%,实测值与预估值的相关性系数R2达到了0.917 6,车辙模型预测精度满足要求。
