巧用消去法

黄旭军

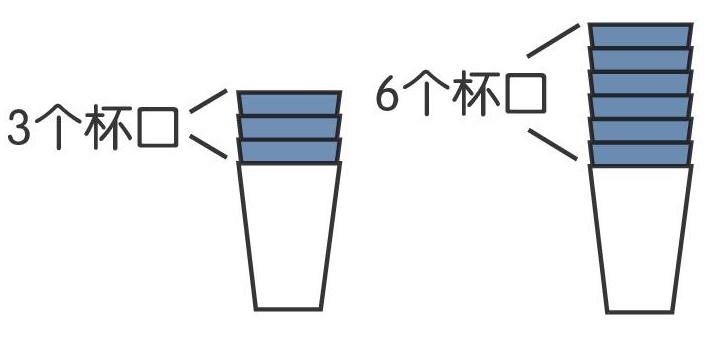
今天这节数学课，老师拿出了两摞杯子，用尺子量了量后，乐呵呵地问： “谁能快速算出每个杯子有多高？”

一石激起千层浪，教室里一下子热闹起来。

“设未知数x，用方程解！”

“老师，直接量！”

……

“还有其他方法吗？”老师问。

“用消去法算！”班长接着说，“把左边看成是3个杯口加1个杯子的高度，右边看成是6个杯口加1个杯子的高度。然后，两边同时消去1个杯子和3个杯口，右边就剩下3个杯口的高度，24-18=6（厘米），那么杯子的高度就是18-6=12（厘米）。”

“没错，当题中有多个量时，我们可以先用消去法消掉一些量，再逐个‘击破其他的量。‘消去用得好，解题没烦恼！”说完，老师开始举例讲解。

例1 3袋大米和5袋面粉共重135千克，9袋大米和4袋面粉共重240千克。6袋大米比1袋面粉重多少千克？

观察开始

已知条件很多，可以先用消去法求出一部分量，再求问题。这里每个量的数量不一样，需要利用倍数关系进行转换。

常规思路

为了便于分析，先把已知条件用等式表示出来：

3袋大米+5袋面粉=135（千克） （1）

9袋大米+4袋面粉=240（千克）  （2）

通过比较，发现只要把（1）式中的每一项都扩大3倍，就可以得到新等式“9袋大米+15袋面粉=405（千克）”。

再比较（2）式和新等式，发现405-240=165（千克），就是15-4=11（袋）面粉的重量。那么，每袋面粉重165÷11=15（千克），每袋大米重（135-15×5）÷3=20（千克）。

所以，6袋大米比1袋面粉重6×20-1×15=105（千克）。

另辟蹊径

仔細观察一下，我们可以发现消去法的另一种用法。

把等式中的排列顺序倒过来：

9袋大米+4袋面粉=240（千克）

3袋大米+5袋面粉=135（千克）

两式相减，得6袋大米-1袋面粉=105（千克），即6袋大米比1袋面粉重105千克。

常规思路

审题时，如果已知量很多，一般都用消去法消掉一部分，可先列出等式，再思考，这样比较好。

观察开始

根据表中数据列出等式：

1A+3B+4C+5D+6E=1876     （1）

1A+5B+7C+9D+11E=2984    （2）

尝试用（2）式减去（1）式，得2B+3C+4D+5E=1108，问题没解决。

另辟蹊径

观察数据特征，可使题目更简单！

1A+3B+4C+5D+6E=1876      （1）

1A+5B+7C+9D+11E=2984     （2）

让（1）式等号两边同时乘以2，得到新等式：

2A+6B+8C+10D+12E=3752  （3）

（3）式与（2）式比较，正好多了“1A+1B+1C+1D+1E”。也就是说，用（3）式减去（2）式即可得结果，1A+1B+1C+1D+1E=3752-2984=768（元）。

训练一二一

买3张桌子和5把椅子，共用去480元，买同样的6张桌子和3把椅子，共用去519元。买3张桌子和12把椅子共要用多少元？（答案见下期）

上期答案：长方形的面积是15平方厘米，三角形的面积是12平方厘米。