基于经典TSP问题的物流运输任务规划
2020-04-19程铁信
何 慧 程铁信
(天津工业大学经济与管理学院 天津 300387)
一、问题的背景
双十一购物节让众多的商家及购物客户疯狂,物流业在这一天承担超负荷的商品运送任务。随着城市的快速发展,越来越多的大型物流公司集结在城市周边。城市白天不允许货车入城,只能限定在夜间24点至凌晨4点入城。城区按各商业中心商场为圆心,7km为半径的总体外包络为界。城区外运行不受时间限制。
某城市物流集团有B01~B07等7个物流分公司中转站,各中转站均配备一定数量的货车。物流集团需要调配7个物流公司中转站的货车夜间进城收集需要运送的商品,每个收货点收货装载平均大约10分钟。货车执行完任务后需返回原物流公司中转站。货车装载参数:I型货车限装0.6吨,II型货车限装1吨。假设货车城区平均车速25km/h。
根据任务要求,需完成收货目标有A01~A10等10个商业区域,每个商业区域包含数量不等的网销商家,其中中心商城是该商业区域中网销规模较大综合性商场,所有商业区域的商家的具体坐标参数见表1,假设每个网销商家之间都有道路相连,路长简化为直线距离。
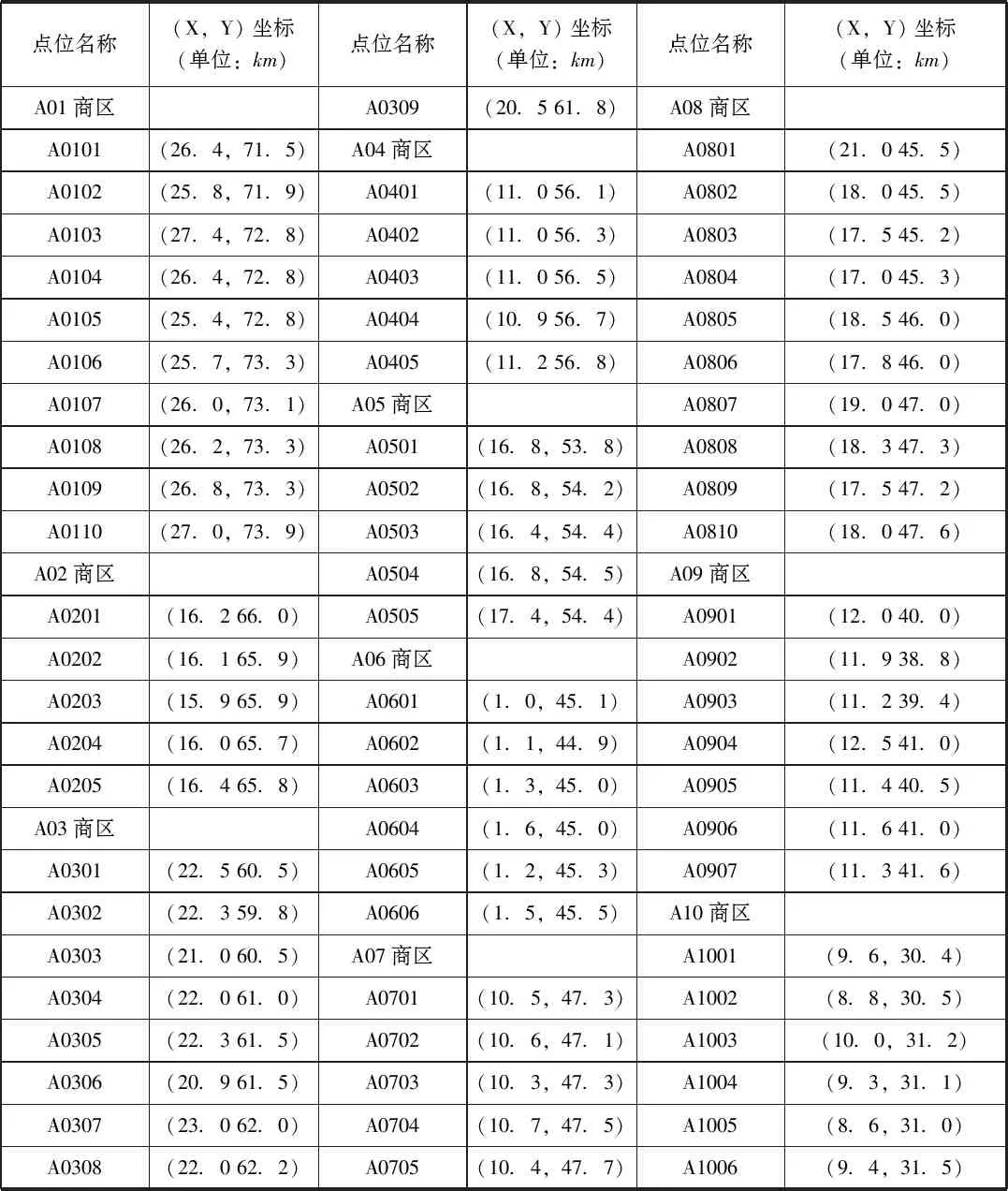
表1 物流分公司中转站的相关信息
二、文献综述
邓先瑞、于晓慧、李春艳等人提出一种基于种群分类粒子群算法的物流区域配送中心车辆运输路径调度优化方法,建立配送中心车辆运输路径调度的数学模型,目标函数为最短配送路径,通过粒子群算法对车辆调度数学模型进行求解,完成配送中心车辆调度的协调性优化,该方法可以合理的选择运输路径,但不能合理的完成车辆运输路径的装载[1]。张倩、鲁渤、杨华龙提出了一种物流区域配送中心车辆路径的鲁棒优化方法,该方法根据算例对车辆路径的鲁棒性度量指标效果进行分析,对适用于车辆运输路径方案的鲁棒性指标进行选择,通过两阶段优化算法完成配送中心车辆运输路径调度的协调性优化,该方法可以合理的对车辆运输路径进行装载,但得到的运输路径不合理[2]。
三、模型的建立
本文要求在不考虑装载容量及运输成本的情况下,确定行车方案,使得所有运货车辆在城内的运送工作时间总和最短。在车辆匀速行驶的条件下,要使运送工作时间总和最短,即要求车辆行驶路径最短。由于不需要考虑每辆车的装载容量,所以首先派出一辆车入城收货,遍历所有的收货点,求这辆车的最短路径,这样就成为一个典型的旅行商(TSP)问题。然后建立单目标多约束的线性优化模型,调用蚁群算法求解模型。再运用逐步推进法确定第一辆车的行驶路径,判断是否需要加派车辆,完成本文中的最短行驶时间的目标。
(一)建立求解各个商区内最短路径的模型
1.选取决策变量
由于匀速行驶,计算一个商区内的最短行驶时间,等价于计算最短行驶路径,即转化成典型的旅行商问题。选取货车从收货点i到收货点j的整数型0-1变量xij、收货点i和j之间的行驶距离dij为决策变量。
2.确定目标函数
以最短行驶时间为目标,建立一个商区内的单目标多约束的线性优化模型。以商区A01为例建立模型,选取货车在该商区内运行时间函数t:
式中,dij为两个收货点i和j之间的行驶距离,v为货车行驶的速度,由题目知v=25km/h,定义0-1整数型变量xij=1表示货车从收货点i到收货点j,否则xij=0,10为每个收货点收货的时间,n为每个商业区商场的数量。
3.对目标函数做以下约束:
(1)货车到达收货点i后,接下来的目的地j只能有一个:
(2)对于收货点j,只能由一个收货点i出发到达此处:
(3)确保货车行驶路线中没有子回路的产生:
问题一与TSP的不同在于终点的不同,TSP问题的终点即起点,根据题意问题一的终点是最后一个收货点。
xi1i2+xi2i3+…+xik-1ik≤k-1(i1,i2,…,ik=1,2,…,n;k=2,3,…,n-1)
(4)判断货车经过收货点i后是否紧接着要经过收货点j:
综上所述,货车在A01商区内的线路优化模型为:
(二)建立求解城内最短路径的模型
基于已知相关数据,以货车在城区内进行货物运送的路线为研究对象,求其最优行车路线和货车调度策略。先考虑只派出一辆货车的情况,求得两个商业区域间的运送时间最短的方案。然后判断该车接下来是直接回中转站还是去邻近商区,若去邻近商区的时间比从中转站重新派车的时间长,则需要重新派车。在每一个商业区收货结束后都需要重复判断,直至最后一个中转站。从而实现调度分配与行车路线规划。本题以时间最短为目标,建立单目标多约束的货车行车路线线性优化模型。
1.选取决策变量
因为货车匀速行驶,行驶时间最短等价于行驶路程最短,又已知各个商场的坐标中转站的坐标,所以选取任意两点之间的运行时间fk为决策变量。
2.确定目标函数
为了使所有运货车辆在城内的运送工作时间综合最小,选取总时间函数T:
其中fk为货车在第k个商业区域内的运送工作时间。
3.确定约束条件
(1)判断某商区是否由某物流中转站派出货车:
其中,l指的是第l个中转站,k指的是第k个商区。
(2)计算每个商区内的运送工作时间
dlk1表示从第l个中转站派车去第k个商区的第1个商场在城内所经过的距离,dkn1表示从第k个商区的第n个商场收货完成后回到第l个中转站的城内的距离。
(3)每个物流中转站在派车时,需要考虑中转站自身的货车数量。需满足派出的货车数量小于等于该中转站的货车数量的条件:
式中,对商区的某个中转站派遣货车数量累计求和,小于等于该中转站总货车数量,其中,货车数量上限分别为n1=3,n2=2,n3=3,n4=2,n5=3,n6=2,n7=3。
(4)物流中转站派出的货车数量应满足是非负整数
ni∈N
式中,N表示物流中转站可派的货车数量,i表示物流中转站的标号。
(5)为了能有效完成所有商业区的货车运送任务,不考虑装载容量和运输成本的条件下,至少需要派出一辆货车进行运送,因此有以下约束:
综上所述,货车行车路线优化可以归结为以下模型:
四、模型的求解
(一)蚁群算法求解TSP问题
由于在某一商区区域内的货车行驶时间最短问题可以转换为TSP问题,且蚁群算法采用了分布式并行计算机制,易于与其他方法结合,具有很强的鲁棒性,因此我们选用蚁群算法来解决TSP问题,该算法基本步骤如下:
step1:首先初始化,设迭代次数为NC,初始化NC=0;将m只蚂蚁置于n个顶点上;初始化信息素及其他参数。
step2:进入循环,按照分段函数计算全局转移选择因子,计算转移概率,m只蚂蚁按概率函数选择下一座城市,完成各自的周游。设蚂蚁k当前所在顶点为i,那么蚂蚁k由点i向点j移动要遵循概率函数而迁移选择下一点。
step3:判断第k只蚂蚁是否到达终点,若到达终点,则k=k+1,否则返step2;记录本次迭代最佳路线,按照蚂蚁行驶路径更新局部信息素。
step4:判断所有蚂蚁是否完成搜索,若全部完成搜索,进行全局信息素更新,否则返回step3。
step5:达到循环结束的条件后,循环停止,输出计算结果最优路径,否则NC=NC+1。
(二)确定商区内最短行车路线
由于每个商业区域内的收货点比较密集,若不只派一辆车进入同一个商区收货,将会使货车在城区内的运行时间及成本大大提高,不满足题意及实际需求,因此可以将每一个商区都视为一个TSP问题,但不需要考虑再返回起点。使用蚁群算法对每个商区内行车路线进行求解,得到的结果如表2:

表2 每个商区内最佳行车路线
(三)计算所需车辆数
根据固定的收货点和物流中转站,可以求解出货车在相邻两个商区收货点之间行驶的时间。当货车在上一个商区收完货物之后,需判断直接回中转站还是继续去下一个商区。

图1 判断是否新增货车示意图
如图1所示,若线段a+b+c+d>a+c+e,则说明货车不返回直接去下一商区的时间更短,无需新增货车;否则新增一辆货车,沿线段d入城收货。
经判断发现,货车从06商区A0606收货点前往10商区A1003收货点的时间大于从A0606到城区边界与从A1003到城区边界的最短时间之和,因此需派两辆车进行货物运送,其中第一辆车运送范围为A01-A07商业区,第二辆车运送范围为A08-A10商业区。
五、总结
本文在求解满足目标条件下的最优运输路径时,考虑到每个商区内收货点分布比较密集,最好用同一辆车进行运送,因此首先将每个商区视为一个整体,将其转化为TSP问题,从而使用蚁群算法求解出每个商区内的最优路径;后来经过判断共需两辆车后,再分别将两辆车的行驶范围看作一个TSP问题,便于求解出满足目标的最优方案,这样既将问题简化,同时又符合实际。
