3类3-正则图中的1-因子数*

唐保祥，任 韩

(1.天水师范学院数学与统计学院，甘肃 天水 741001;2.华东师范大学数学系，上海 200062)

研究图的1-因子计数问题[1-4]有重要的理论价值和现实意义,其研究成果已应用于多个领域.分类嵌套递推方法,是求图的1-因子数的一种非常有效的方法[4-6].笔者拟利用分类嵌套递推方法给出3类特殊3-正则图的1-因子数的计算公式.

1 预备知识

定义1若图G的2个1-因子M1和M2中有1条边不同,则称M1和M2是G的2个不同的1-因子.

定义22条长为n的路为P1=u0u1…un,P2=v0v1…vn,分别连接路P1与P2的顶点ui与vi(i=0,1,…,n)所得到的图,称为长为n的梯子,记为Ln.

引理1[4]长为n的梯子Ln的1-因子数用m(Ln)表示,其中n=1,2,3,…,则

2 主要结果及其证明

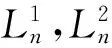
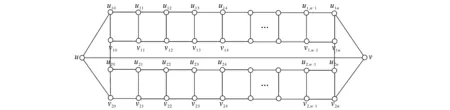
图1 2-Z-Ln

(1)

证明图2-Z-Ln是3-正则3边连通图,显然存在1-因子.图2-Z-Ln的1-因子按饱和顶点u可分如下几种情形求得:

情形1n为奇数.

(ⅱ)由m(Ln)的定义,若图2-Z-Ln某个1-因子包含边uu10,v10u20,则该1-因子一定包含边v20v21,u21u22,v22v23,…,v2,n-1v2n,u2nv1n,vu1n,故这类1-因子数为m(Ln-1).

由(ⅰ)(ⅱ)可知,图2-Z-Ln包含边uu10的1-因子数为m(Ln)+m(Ln-1).由图2-Z-Ln对称性可知,包含边uv20的1-因子数也为m(Ln)+m(Ln-1).

(ⅲ)由m(Ln)的定义,图2-Z-Ln包含边uv,u10u11,v10v11的1-因子数为m(Ln-2)·m(Ln).

(ⅳ)若图2-Z-Ln的某个1-因子包含边uv,u10u11,v10u20,则该1-因子一定包含边v11v12,u12u13,v13v14,…,u1,n-1u1n,v1nu2n,v20v21,u21u22,v22v23,…,v2,n-1v2n,故这类1-因子数为1.

(ⅴ)由m(Ln)的定义,图2-Z-Ln包含边uv,u10v10的1-因子数为m(Ln-1)·m(Ln).

于是,当n为奇数时,图2-Z-Ln的1-因子数为

σ(n)=2m(Ln)+2m(Ln-1)+m(Ln-2)·m(Ln)+m(Ln-1)·m(Ln)+1.

情形2n为偶数.

(ⅰ)由m(Ln)的定义,若图2-Z-Ln某个1-因子包含边uu10,v10v11,则该1-因子一定包含边u11u12,v12v13,u13u14,…,u1,n-1u1n,v1nu2n,v2nv,故这类1-因子数为m(Ln-1).

(ⅱ)由m(Ln)的定义,若图2-Z-Ln某个1-因子包含边uu10,v10u20,则该1-因子一定包含边v20v21,u21u22,v22v23,…,u2,n-1u2n,v2nv,故这类1-因子数为m(Ln-1).

由(ⅰ)(ⅱ)可知,图2-Z-Ln包含边uu10的1-因子数为2m(Ln-1).由图2-Z-Ln对称性可知,包含边uv20的1-因子数也为2m(Ln-1).

(ⅲ)由m(Ln)的定义,图2-Z-Ln包含边uv,u10u11,v10v11的1-因子数为m(Ln-2)·m(Ln).

(ⅳ)由m(Ln)的定义,图2-Z-Ln包含边uv,u10v10的1-因子数为m(Ln-1)·m(Ln).

于是,当n为偶数时,图2-Z-Ln的1-因子数为

σ(n)=4m(Ln-1)+m(Ln-2)·m(Ln)+m(Ln-1)·m(Ln).

综上可知，(1)式成立.

定理2设长为n的梯子Ln的顶点集为V(Ln)={u0,u1,…,un,v0,v1,…,vn}.将梯子Ln的顶点u0,un分别与顶点u连接,再将Ln的顶点v0,vn分别与顶点v连接,这样得到的图记为H-Ln,如图2所示.用τ(n)表示图H-Ln的1-因子数,则

图2 H-Ln

(2)

证明图H-Ln是3-正则3边图,显然存在1-因子.图H-Ln的1-因子按饱和顶点u可分如下几种情形求得:

情形1n为奇数.

(ⅰ)由m(Ln)的定义,若图H-Ln某个1-因子包含边uv,则该1-因子一定包含梯子Ln的1-因子,故图H-Ln含边uv的1-因子数为m(Ln).

(ⅱ)由m(Ln)的定义,若图H-Ln的1-因子包含边uu10,vv10,则这类1-因子数为m(Ln-1).

(ⅲ)由m(Ln)的定义,若图H-Ln的1-因子包含边uu1n,vv1n,则这类1-因子数为m(Ln-1).

于是,当n为奇数时,图H-Ln的1-因子数为τ(n)=m(Ln)+2m(Ln-1).

情形2n为偶数.

(ⅰ)由m(Ln)的定义,若图H-Ln某个1-因子包含边uv,则该1-因子一定包含梯子Ln的1-因子,故图H-Ln含边uv的1-因子数为m(Ln).

(ⅱ)图2-Z-Ln的包含边uu10,v10v11,u11u12,…,u1,n-1u1n,v1nv的1-因子数为1.

(ⅲ)由m(Ln)的定义,图H-Ln某个1-因子包含边的1-因子数为m(Ln-1).

由(ⅱ)和(ⅲ)可知,图H-Ln包含边uu10的1-因子数为m(Ln-1)+1.由图H-Ln对称性可知,包含边uu1n的1-因子数也为m(Ln-1)+1.于是,当n为偶数时,图H-Ln的1-因子数为τ(n)=m(Ln)+2m(Ln-1)+2.

综上可知，(2)式成立.

定理3设长为n的梯子Ln的顶点集为V(Ln)={u0,u1,…,un,v0,v1,…,vn}.将梯子Ln的顶点u0,v0分别与顶点u连接,再将Ln的顶点un,vn分别与顶点v连接,这样得到的图记为Z-Ln,如图3所示.用φ(n)表示图Z-Ln的1-因子数,则

图3 Z-Ln

证明图Z-Ln是3-正则3边图,显然存在1-因子.图Z-Ln的1-因子按饱和顶点u可分如下几种情形求得:

情形1图Z-Ln的包含边uv的1-因子.

由m(Ln)的定义,若图Z-Ln某个1-因子包含边uv,则该1-因子一定包含梯子Ln的所有1-因子,故图Z-Ln含边uv的1-因子数为m(Ln).

情形2图Z-Ln的不包含边uv的1-因子.

(ⅰ)当n为奇数时,图Z-Ln的1-因子有2个:一个是图Z-Ln的包含边uu0,v0v1,u1u2,…,vn-1vn,u1nv的1-因子;另一个是图Z-Ln的包含边uv0,u0u1,v1v2,…,un-1un,v1nv的1-因子.

(ⅱ)当n为偶数时,图Z-Ln的1-因子也有2个:一个是图Z-Ln的包含边uu0,v0v1,u1u2,…,un-1un,v1nv的1-因子；另一个是图Z-Ln的包含边uv0,u0u1,v1v2,…,vn-1vn,u1nv的1-因子.

综上可知,无论n是奇数还是偶数,都有φ(n)=m(Ln)+2,于是