DCT与SVD相融合的抗剪切攻击水印算法*

于帅珍，周 健，谢道平

(安徽财经大学电子信息工程系，安徽 蚌埠 233030)

目前，大多数水印算法都能够对滤波、加噪和JPEG压缩等常规图像处理进行有效抵抗，但对剪切、旋转等几何攻击的抵抗效果并不理想.造成这种现象的主要原因是，水印提取时一般需要明确其嵌入位置，常规图像处理仅轻微改变图像的像素值，并不会改变水印信息的嵌入位置；而剪切、旋转等几何攻击会破坏水印信息的同步性，从而无法明确水印信息的嵌入位置，导致提取水印不成功.因此，提高水印系统抗剪切几何攻击的能力是相当重要的.近年来，关于抗剪切攻击的水印系统算法研究出现了不少成果[1-6]，但大多数的抗剪切水印算法其剪切面积不能超过1/2，即使有的算法其剪切面积可以超过1/2但不能进行任意方向、位置的剪切，因此这些算法不能完全抵抗剪切攻击，更不能抵抗组合攻击.为了克服这些缺点，笔者拟结合对常规图像处理具有较好抵抗能力的DCT变换和对几何攻击具有较好鲁棒性特点的SVD变换[7-8]，设计一种多变换域分块水印算法.

1 算法的相关理论

1.1 离散余弦变换与奇异值分解

1997年，Cox等[10]提出在图像视觉最重要的区域嵌入水印，能够提高水印系统的鲁棒性.载体图像经过DCT变换后得到频率系数矩阵，其左上角的系数幅值最大，是视觉最重要的区域.该系数在水印信息嵌入过程中相当于一个强背景，可增强水印信息的嵌入量，进而提高水印系统的抗攻击能力.若对整幅图像进行DCT变换，则只能得到1个最大系数幅值.根据JPEG方案中的分块思想对载体图像先分块，再对每一分块进行DCT变换，就可以得到许多最大系数幅值.在这些最大系数幅值中植入水印，在增强其嵌入强度、嵌入量的同时还可以将水印信息均匀地分布在载体图像的各个区域，提高水印系统的抗剪切等几何攻击能力.

图像奇异值本身有较强的稳定性(即当图像受到较小的扰动时，其奇异值变化甚微)，且奇异值对几何失真具不变性，因此其抵抗几何攻击的能力较强，从而将水印信息植入奇异值矩阵中可以增强水印系统的抗攻击性[11].

1.2 Aronld加密

对水印信息进行Aronld加密处理，经加密处理后的图像因像素与像素之间的关系发生了改变而变得混乱.将这些混乱的信息放在载体图像中，一旦遭受攻击就会有水印信息损失，对有损失的水印信息进行反置乱处理后其损失会分散到整个图像的各区域中，提取的水印整体性较好.直接利用Aronld加密公式

进行加密，只有置乱次数作为密钥，这种操作虽然简单，但是难以抵抗穷举攻击.

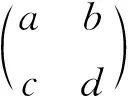
2 DCT与SVD相融合的图像水印算法

2.1 水印嵌入算法

采用分块方法，将置乱的水印信息嵌入到DCT与SVD相融合的区域中.嵌入算法具体步骤如下：

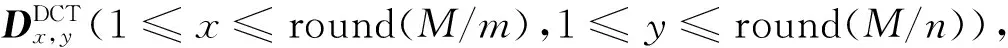
(ⅱ)利用公式(USV)=svd(A)对矩阵A进行SVD变换，得到矩阵U，V，S.

(ⅲ)利用变形后的Arnold变换算法置乱水印图像，得到加密后的水印W1.

2.2 水印检测算法

水印检测算法是水印嵌入算法的逆过程，其具体步骤如下：

3 实验结果与讨论

3.1 未受攻击测试

本实验采用图1(a)所示的原始载体图像(512×512)和图1(b)所示的原始水印图像(64×64)，水印强度调节系数λ=0.1.图2(a)是未受攻击的含水印图像，其峰值信噪比为54.367.观察图1(a)和图2(a)，2幅图像几乎没有区别，说明DCT与SVD相融合的水印算法具有较好的不可见性，能够很好地将水印信息隐藏在载体图像中.提取的水印图像如图2(b)所示，它与图1(b)的相似度等于1.再观察图2(b)和图1(b)，2幅图像也几乎没有区别，说明DCT与SVD相融合的水印算法能够准确地检测到水印，达到了保护数字图像版权的目的.

图1 原始图像和水印图像

图2 未攻击测试

3.2 单一剪切几何攻击测试

对含水印的图像进行各种单一剪切攻击后提取的水印如图3所示，从中可见水印轮廓都非常清晰.从单一剪切攻击后水印检测结果(表1)可知，当剪切面积小于等于1/2时相似度很高(不小于0.945 5)，误码率很低(不大于0.024 0)，当剪切面积为3/4时，相似度仍为0.832 6，由此判断DCT与SVD相融合的水印算法的剪切攻击方案对水印信息的破坏较小，且随着剪切面积的减少，检测出的水印图像的清晰度逐渐提高.表2是DCT与SVD相融合的水印算法与基于人眼视觉特性的DWT-SVD水印算法[3](算法1)、基于Walsh变换和Hessenberg分解的水印算法[4](算法2)、基于HVS和Hessenberg分解的水印算法[5](算法3)经单一剪切攻击后提取水印的相似度比较结果.从表2可知，DCT与SVD相融合的水印算法的相似度高于其他3种算法，说明该算法抗单一剪切攻击的能力很强，完全能够抵抗单一剪切几何攻击.

图3 单一剪切攻击

表1 单一剪切攻击后水印检测结果

表2 4种算法剪切攻击提取水印的相似度比较结果

3.3 旋转后再进行剪切联合几何攻击测试

水印系统除了会遭受单一攻击之外，更多情况下还会遭受联合攻击，鲁棒水印系统的抗几何攻击仍然是目前要解决的难点.为了验证DCT与SVD相融合的水印算法的抗联合几何攻击的能力，首先对含水印的图像进行任意角度旋转，然后在其中心剪切1/4.检测出的水印图像如图4所示，从中可见水印图像仍然非常清晰.提取的水印信息见表3，从中可知相似度都大于0.979.由此可知，DCT与SVD相融合的水印算法完全能够抵抗旋转和剪切的联合几何攻击，因而更能抵抗单一的旋转几何攻击.

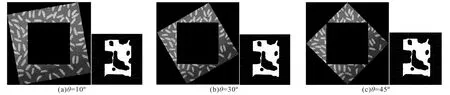
图4 旋转和剪切联合攻击

表3 旋转和剪切联合攻击后水印检测结果

3.4 JPEG压缩后再进行剪切联合几何攻击测试

对含水印的图像进行先有损压缩，再在其中心剪切1/4的联合攻击测试，攻击结果如图5和表4所示.结合图5和表4可知：品质因数Q≥50的联合攻击，其提取的水印相似度皆大于0.98，误码率低于0.006 8；Q=10时图像受损比较严重(图5(b))，在这种情况下中心再剪掉1/4，提取的水印信息相似度为0.920 4，图像边缘轮廓仍然很清晰；Q=1时图像出现非常明显的方块效应(图5(c))，提取的水印信息相似度虽然为0.786 6，但是检测出的水印图像仍然较清晰.由此可知，DCT与SVD相融合的水印算法完全能够抵抗JPEG压缩和剪切联合的几何攻击.

图5 压缩和剪切联合攻击

表4 JPEG压缩和剪切联合攻击后水印检测结果

3.5 缩放后再左剪切1/4的联合几何攻击测试

对含水印的图像进行先缩放再剪切的双重几何攻击，攻击结果如图6和表5所示.结合图6和表5可知，DCT与SVD相融合的水印算法对抵抗先放大后剪切攻击的能力高于先缩小后剪切.原因在于，对图像进行缩小几何攻击时其重要信息会丢失，所以提取的水印信息的清晰度和相似度都有所降低；对图像进行放大几何攻击时其重要信息不会丢失，所以提取的水印信息的清晰度和相似度的降幅不大.

图6 缩放、剪切联合几何攻击

表5 缩放、剪切联合攻击后水印检测结果

3.6 其他联合攻击测试

实际上，水印系统不仅应该具有抵抗剪切等几何攻击的能力，还应该具有抵抗常规图像处理的能力.对含水印的图像先进行常规图像处理再进行剪切攻击，攻击结果如图7和表6所示.结合图7和表6可知：当噪声攻击的方差为0.1时，图像污染相当严重，此时再进行剪切攻击，提取的水印相似度仍为0.98以上，检测出的水印图像非常清晰；对图像进行中值滤波后再进行剪切攻击，其相似度也在0.98以上；对图像进行旋转、缩放、剪切3次几何攻击，提取的水印信息相似度仍为0.975.由此可知，DCT与SVD相融合的水印算法抵抗常规图像处理和剪切联合攻击的能力很强.

图7 其他联合攻击

表6 其他联合攻击后水印检测结果

4 结语

目前，大多数水印算法都能够有效抵抗部分常规图像处理和攻击后仍能明确水印位置的几何攻击，而对于攻击后不能明确水印信息嵌入位置的剪切、旋转等几何攻击的鲁棒性虽有所提高但仍不理想，因此，笔者设计了一种将Arnold置乱变换、DCT变换、SVD变换相融合的抗剪切水印算法.该算法不仅能够完全抵抗单一的剪切攻击，而且对图像先压缩再剪切的联合攻击、先旋转再剪切的联合攻击，以及各种常见攻击再剪切的联合攻击的鲁棒性都较强，甚至对图像进行缩放、旋转再剪切3次几何攻击后仍然能够提取清晰的水印.在水印图像嵌入前用Arnold变形公式对其进行置乱处理，在多密钥的作用下保证了算法的安全性.