中考“面积问题”的教学实践与思考

周青

摘要：近年来，各地中考中频频出现“面积问题”的试题，成为中考数学中的一个必考知识点。“面积问题”题型较多，知识综合，方法灵活，笔者以近几年各地区中考数学试题中涉及的面积问题为载体，针对面积问题的类型和解决问题的策略，思考面积问题在教学实践中的意义。

关键词：面积问题；中考；教学实践

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2020）11-0117

问题是数学的心脏，学习数学的主要目的在于解决问题。好的数学问题应与学生的实际生活有着直接的联系，应当具有较强的探索性、现实意义和趣味性以及知识性。面积问题是数学知识结构中的“连结点”，其常结合一次函数、反比例函数、二次函数、三角形全等和相似、四边形、圆等初中数学核心内容成为考试试题。

一、认识：面积问题的类型

面积问题为学生提供了一个观察、分析、猜想并进行说理验证的探究模型，以图形的运动变化为策略，使学生能在一个动态的数学情境中感悟知识的发生和发展过程，探索问题的结论和规律的变化，真正理解图形的性质。

1.公式法

分析：在Rt△OBC中求出OB、BC，然后求出扇形OAB及△OBC的面积即可得出答案。本题考查了扇形的面积计算，解答本题关键是求出扇形的半径，熟练掌握扇形的面积公式。

面积问题，有的是直接计算面积，有的是以面积为条件求其他，更多的情况是由图形的运动引起图形的变化，从而建立面积函数关系。中考命题中如何从具体情境中抽象出数学材料，并将获得的材料符号化，体现基础性、应用性、实践性、开放性、探究性，这是中考数学试题的重要特征。

2.割补法

分析：根据弦AB=BC，CD=DE，可得∠BOD=90°，过点O作OF⊥BC于点F，OG⊥CD于点G，在四边形OFCG中可得∠FCD= 135°，过点C作CN∥OF，交OG于点N，判断△CNG、△OMN为等腰直角三角形，分别求出NG、ON，继而得出OG，在Rt△OGD中求出OD，即得圆O的半径，代入扇形面积公式求解即可。

学习数学知识是学生主动构建知识体系的过程，学生只有通过自身的操作活动和主动参与学习的数学才是有效的。在学生动手操作、探究的过程中，逐步形成分析、判断、推理、归纳、表达等能力。

3.整体法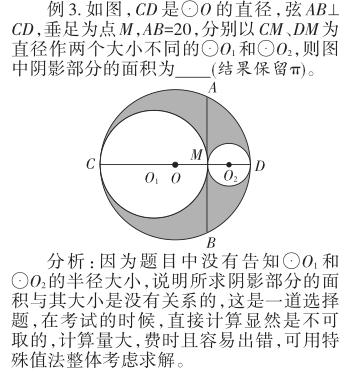

二、实践：面积问题的解题策略

数学来源于生活，同时也必将应用于生活，学数学就是为了解决生活中所碰到的实际问题。近几年的中考题相当注重运用数学知识解决实际问题的考查，考查层次非常丰富，不同水平的学生可以充分展示自己不同的探究深度，以及综合运用数学知识、思想方法去探索规律、获取新知的能力。

“能使學生获得受用终生的东西的教育，才是最高尚最好的教育。”数学思想方法的教学，正是这样一件富有意义的工作。对于学生来说，不论将来从事什么工作，唯有深深地铭刻于头脑中的数学精神、数学的思维方法、研究方法，可以随时随地会发生作用，使他们受益终生。

（作者单位：浙江省台州市路桥区新桥镇初级中学318050）