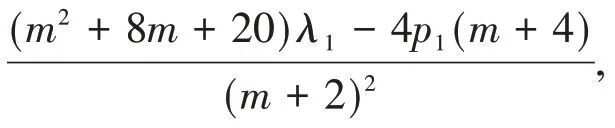调和算子多项式广义次谱的显式上界

黄振明

（苏州市职业大学 数理部，江苏 苏州 215104）

1 Introduction and Statement of Result

Let Pt(x) be a polynomial of degree t (t ≥2)as Pt(x) = ptxt+ pt-1xt-1+ …+ p1x + p0，where pt= 1,pi≥0 (i = 0,1,…,t - 1)are real numbers.The following spectrum problem of polynomial of harmonic operator Pt(-Δ)has been extensively studied by many mathematical researchers:

and obtained an explicit inequality estimating the upper bound of the secondary spectrum in terms of the linear function of the principal one[1].

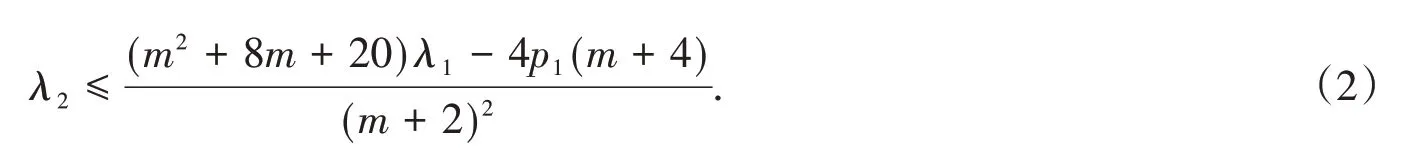
In this paper we further study a more general situation of Problem(1),that is the generalized problem of polynomial operator Pt(-Δ)

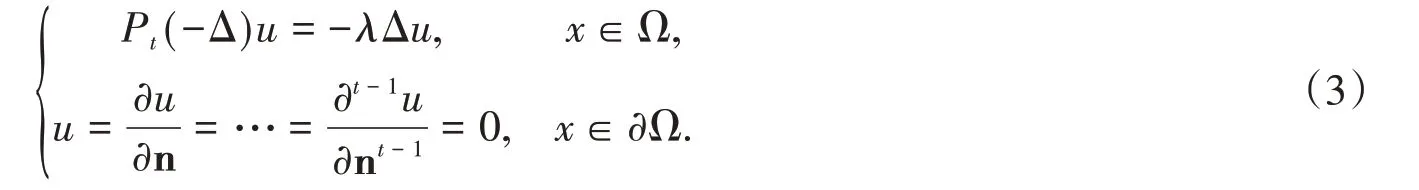
To our knowledge, the general case（3）has not been studied previously. For any positive integer t(t ≥2) in Problem（3）, we established an explicit upper bound for the secondary spectrum in terms of the principal one. The inequality we gained is called universal inequality because it does not involve domain dependence.This proof is similar in spirit to that of Carston and Dietmar[2].Indeed,we have the following theorem after some complicated work.

Theorem 1 Let λ1,λ2be the principal and secondary spectrum of Problem（3）.Then

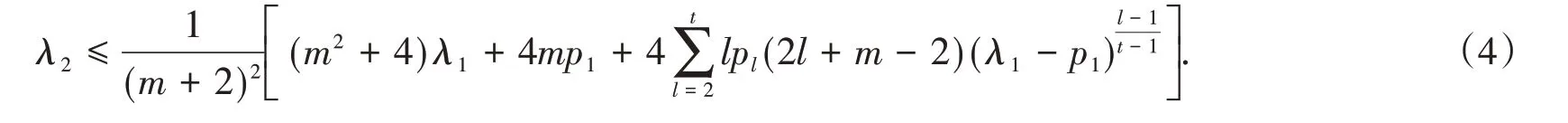
2 Proof of Theorem 1

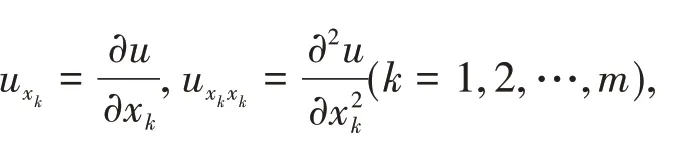
We multiply(3)by u,integrate by parts,use the boundary conditions and(5),this gives

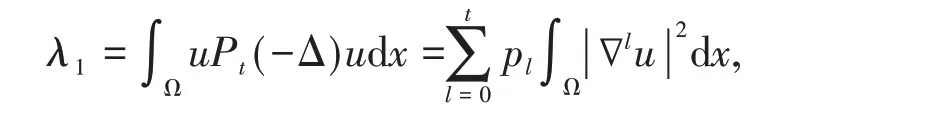
thus we have

Using the definition of φkand（3）,one obtains

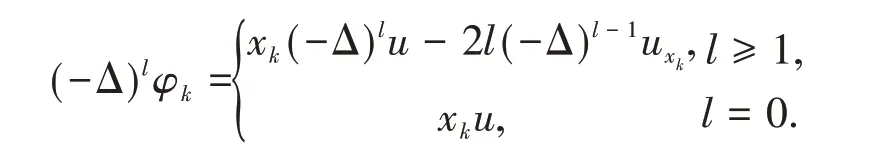
and

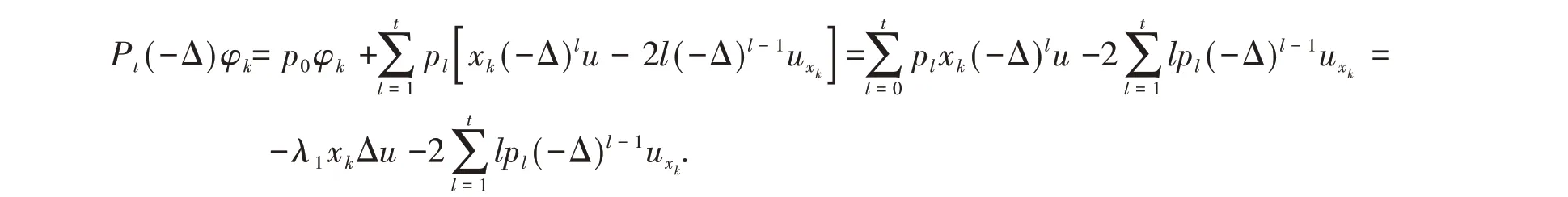
Therefore,we have

On the other hand,using integration by parts,we obtain

which gives

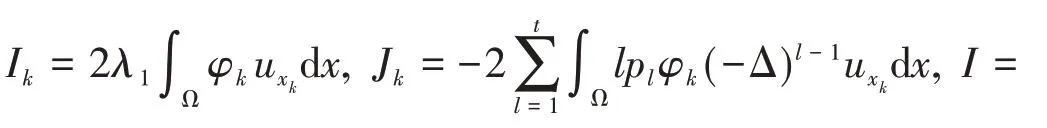
Combining(7)with(9),yields

Lemma 1 Suppose that u is an eigenfunction of Problem (3)corresponding to the principal spectrumλ1with∫Ω|∇u|2dx = 1.Then

Proof (a)Let us first prove the following inequality

This is done by mathematical induction. For s= 1, using integration by parts, Schwarz’s inequality and（5）,meanwhile noting the boundary condition in（3）,we have

so（11）is correct for s= 1.

Assume（11）is true for some fixed s= k - 1(k ≤t - 2).Then,using integration by parts,Schwarz’s inequality and the boundary condition again,we have

after simplified,it turns out

so the inequality（11）is true for s= k,and we are done.

Using（11）repeatedly to∫Ω||∇1+su2dx,combining（6）we have

that completes the proof.

（b）Similarly,using（5）,integration by parts,Schwarz’s inequality and Lemma1（a）,we have

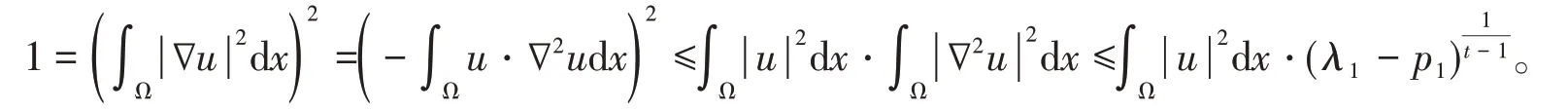
This finishes the proof of Lemma1（b）.

Lemma 2 Let u be an eigenfunction of Problem（3）corresponding to the principal spectrumλ1,and φkbe as above.Then we have

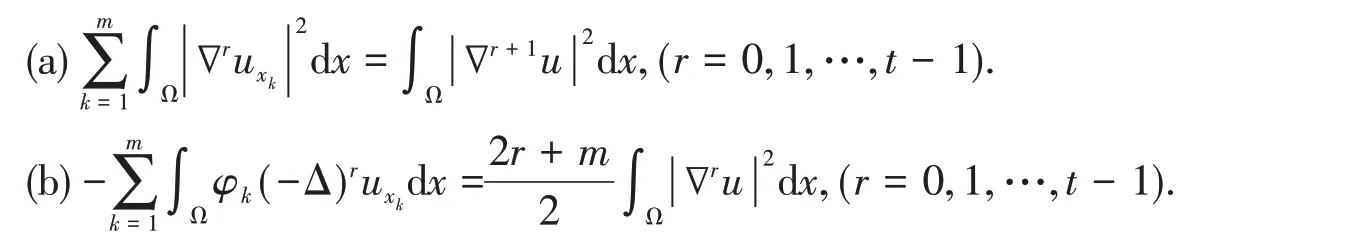
Proof （a）Using integration by parts and the definition of the harmonic operator,we have

so Lemma 2（a）is proved.

（b）When r ≥1,using integration by parts,we have

so,we get

Using Lemma 2（a）,we have

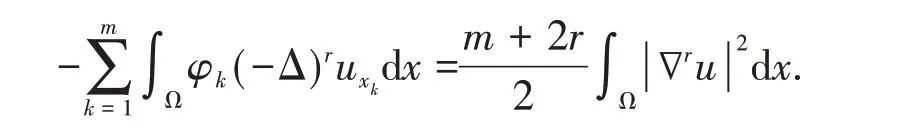
When r = 0,with the similar process,we obtain

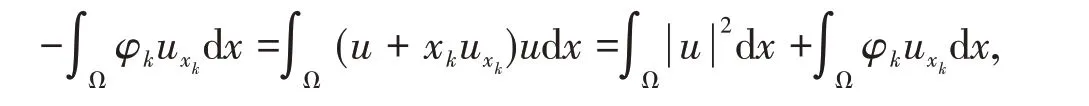
thus

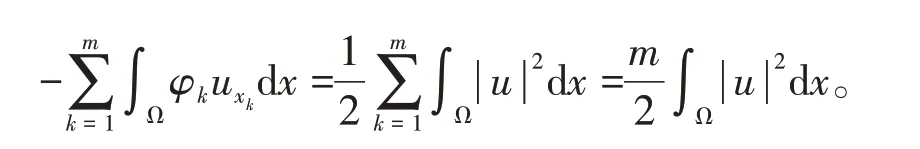
This finishes the proof of Lemma 2（b）.

Lemma 3 For I,J defined as above,the following estimate holds

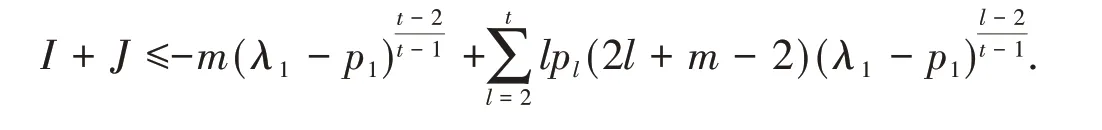
Proof Using Lemma 2（b）to I and the first term of J respectively,we have

and

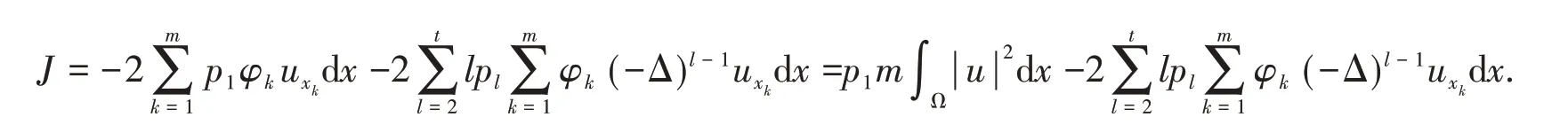
Using Lemma 1（b）,Lemma 2（b）and Lemma 1（a）,we obtain

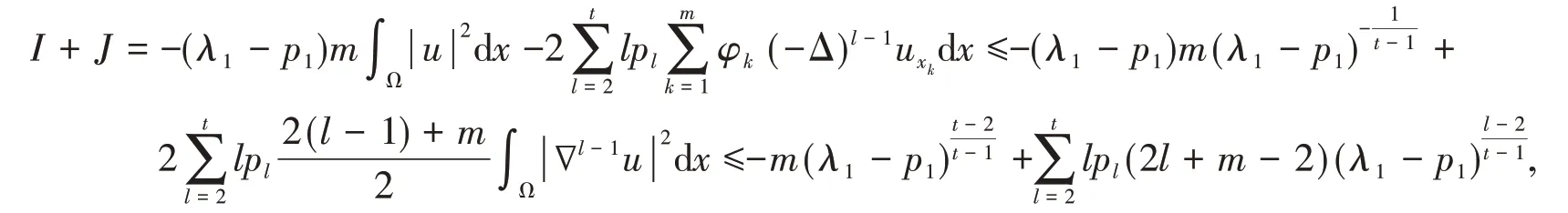
thereby we complete the proof of Lemma 3.

Lemma 4 Let φkand λ1be as above.Then

Proof Using the homogeneous boundary condition of φkand u, integration by parts, Lemma 2（b）and（5）,we have

By Young’s inequality with ε,（12），Lemma 2(a)and Lemma 1(a),one gets

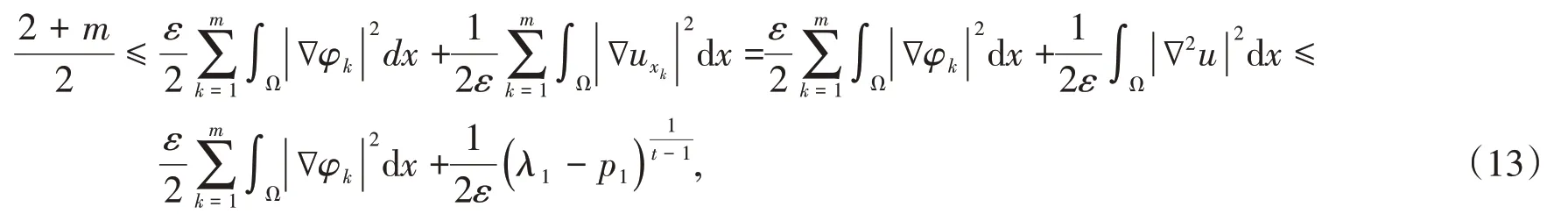
where ε ＞0 is an arbitrary constant.The right-hand side of（13）assumes its minimum at the point

at which we obtain the inequality

thus finishing the proof of Lemma 4.

Proof of Theorem 1 We rewrite（10）as

Lemma 4 can be read as

Therefore, substituting Lemma 3 and（15）into（14）, we derive the inequality（4）in the Theorem 1 immediately after simplified.