基于多元线性回归的渡槽变形预测模型研究
2020-04-18江守燕赵林鑫杜成斌王琨荃
江守燕 赵林鑫 杜成斌 王琨荃
(河海大学 工程力学系,南京210098)
对工程结构的安全监测数据应用数学方法,建立效应集与荷载集之间的关系,来模拟结构变化和预测发展趋势,是实现对大坝、渡槽等水工结构的安全健康监测的有效手段[1-3].其中常采用的数学模型有统计模型、确定性模型、混合型模型等[4-6].基于多元线性回归(multiple linear regression,MLR)的统计模型广泛应用于岩土、交通、气象等行业中工程量的预测[7-9].吴中如院士[10]指出从温度因素、回归分解的角度来说,将统计模型应用于工程结构的安全监控具有较高的精度、工作量小,是可取的方法.
渡槽建造于地面高处,在输水过程中,其安全问题为重中之重[11],然而由于时间的积累,渡槽结构受气候、地理环境、水位变化、人群荷载、风荷载等影响,耐久性能老化;另一方面由于国内某些历史久远的渡槽建设之初,受制于当时设计条件,加上运营期间不注重维护,导致部分渡槽存在安全隐患.结构变形是评价混凝土结构安全程度和服役状况的一个重要指标[12].因此,为了对渡槽进行安全评估,建立适当的监控模型,定量分析温度、水位、时效对渡槽变形的影响,尤为重要.其中,槽墩的工作状态对渡槽整体结构的稳定安全起着决定性的作用,槽墩承担着水载荷、上部结构的自重,通过墩身及下部基础将荷载传给地基,所以槽墩沉降量的监测对渡槽的安全至关重要.传统的数理统计模型因其计算快,并且能够分析模拟出工程数据中因变量与影响因子的直接关系式,给出具体的各个自变量的回归系数,从而获得广泛应用,比如多元线性回归(multiple linear regression,MLR)、多元逐步回归(stepwise regression)、多项式回归(polynomial regression)等模型.然而由于建立模型时样本选择具有人为性[13-14],为了掌握基于MLR 的变形监测模型的预报能力,将此方法应用到工程实例上进行分析时,需要确定数量适合的训练样本和预测样本,以便对渡槽变形进行短期预测.
本文采用MLR 统计模型建立渡槽变形安全监测模型,将其与MSR模型的结果进行比较,并探究训练样本与预测样本的比例对预测精度的影响.研究从模型的预测精度角度探讨MLR 模型在渡槽安全监控领域的应用,对渡槽结构健康监测具有重要意义.
1 渡槽沉降预测的监控统计模型
渡槽工程中的监测物理量大致包括两类:第一类为荷载,如水压力、温度荷载、地震荷载;第二类为荷载所产生的效应量,如沉降、应力、应变.通常把效应量作为因变量y,荷载作为自变量xi(i=1,2,…,k),建立二者之间的数学模型.在水压力H、温度T、时效θ 等荷载的作用下,渡槽槽墩将发生沉降变形.假设沉降量y按其成因分为水压分量yH、温度分量yT、时效分量yθ,给出渡槽变形表达式
式中:yH为水压引起的渡槽变形分量;yT为渡槽结构混凝土温度变化引起的渡槽变形分量;yθ为时间效应引起的渡槽变形分量;y为渡槽变形沉降量.
考虑yH与水压力呈线性关系,即水压力作用产生的沉降量yH与水位H、H2线性相关,即

式中:ai为水压分量回归系数.
yT是由渡槽主体混凝土和浆砌石温度变化引起的.红旗渡槽运行多年,内部温度受外界周期性变化温度的影响,在布置边界温度计的情况下,考虑yT与混凝土温度成线性关系,因此选取观测i 个边界温度计的气温值yT作为温度因子,即
式中:Ti为第i个边界温度计气温值;bi为温度分量回归系数;n为边界温度计个数.在建模预测的实际过程中发现当温度因子次数适当提高时模型的预测效果优化,因此在实际预测过程中,需灵活选用因子.
随着时间推移,结构服役年限增长,渡槽会因为主体混凝土徐变、地基土压缩变形等原因产生不可逆的变形,建设之初,时效位移变化急剧,在渡槽运行多年后,yθ从非线性变化逐渐变为线性变化,因此采用线性时间函数确定时效变形分量yθ,即
式中:θ=1,2,…,n,其中n表示终测日至始测日的天数;c1为时效分量回归系数.
2 渡槽变形预测建模方法
2.1 测量误差处理
由于统计模型假定每次的观测数据都是独立的,此假定要求工程数据的精确性和可靠性,以便提高拟合预测性能.然而实际工程中由于测量数据受到多种不可控因素影响,比如突然的地动影响或者突然的荷载施加,导致数据中出现一些不符合规律的变化,测量误差由此出现,此时应剔除训练集中不良数据,采用取前后平均值的方法替换不良数据.不良数据的判断方法采用拉伊特准则(3σ准则),即渡槽沉降变形的实测值与监控模型训练集拟合值之间的残差绝对值大于3倍实测值数列的标准差,即
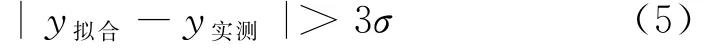
则认为该值为不良数据.当处理完不良数据后,重新进行拉伊特准则检验.计算每个样本点的残差值,并与该组实测值的标准差比较,将满足式(5)的不良数据标出,代之以前后两个样本点的实测平均值.
2.2 模型建立
监控预测模型的数据集包括训练集和测试集两部分,建立模型的过程分为3个步骤:①研究训练集数据,建立监测效应值与荷载之间的联系;②将研究训练集所得到的数学模型应用到测试集数据上,得到监测效应量预测值;③根据评价指标分析预测值的准确性,确定该预测模型在现有的建模误差影响下是否实用,预报误差是否可以接受.
2.3 模型评价指标
在监测数据的回归分析中,为了定量分析预测结果的好坏,需引入评价指标,同时也可对测试集数据的拟合效果进行评价.指标有平均绝对误差(MAE),均方误差(MSE),最大绝对误差(S),复相关系数(R),运行时间(Time).MAE、MSE、S、Time值越小,R值越大,则该模型拟合预测效果越好,表达式如下:
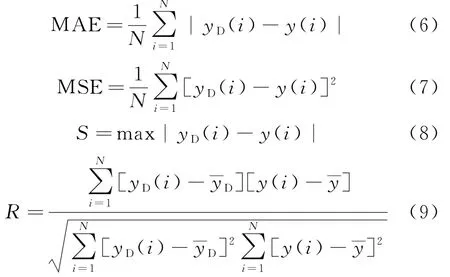
式中:yD和为监控模型对效应值的预测值和平均预测值;y和为实测值及平均实测值.
2.4 多元回归方法
多元回归分析步骤如图1、2 所示,采用MLR、MSR 模型一方面验证传统统计模型的有效性,另一方面对比分析,从预测精度角度考虑,选择适合模型.
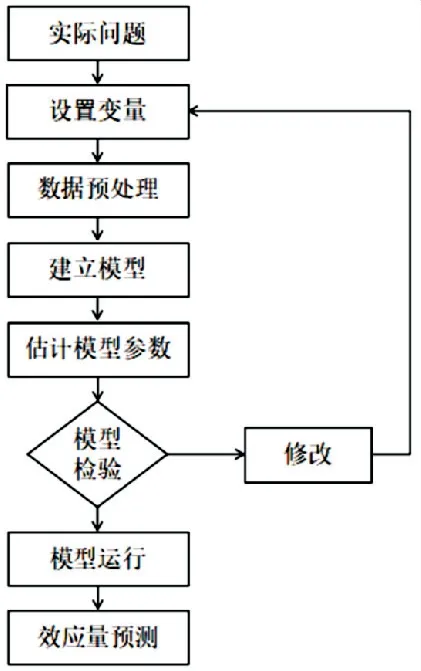
图1 MLR 建模流程图
3 渡槽变形预测模型
3.1 工程概况
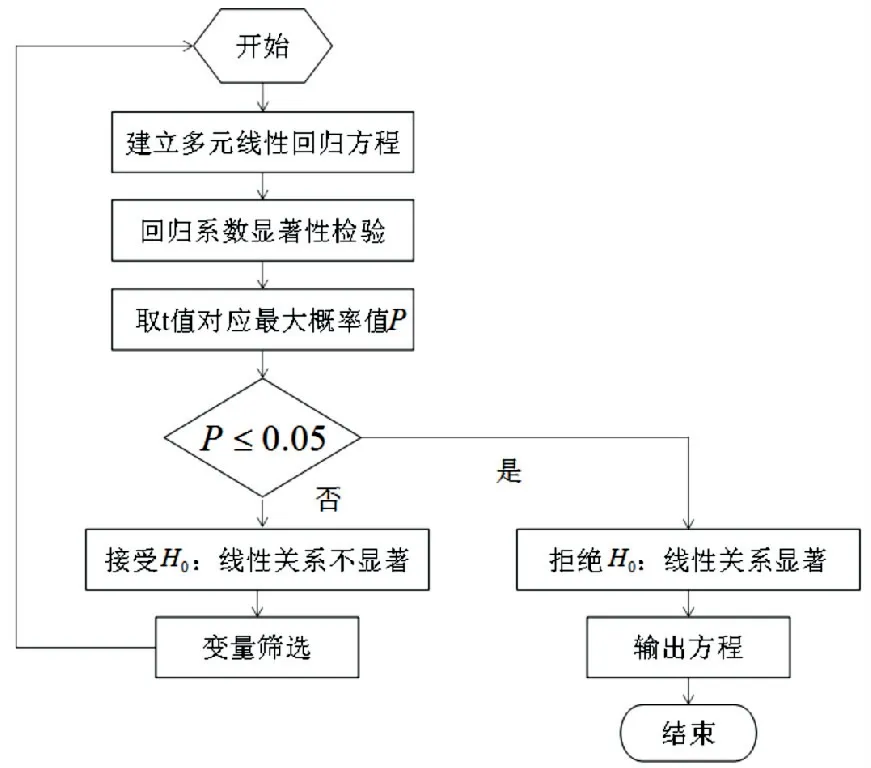
图2 MSR 分析流程图
红旗渡槽属于里石门水库北干渠,设计为变截面悬链线浆砌石拱渡槽.渡槽全长797.5 m,11主跨,每跨56.05 m(净跨53.19 m),计算矢高17.32 m,矢跨比1∶3,槽顶至溪流水面最大高度28 m.相邻两大拱和两端大拱与边墩之间砌筑小拱79个.渡槽槽身宽4.62 m,高4.34 m;梯形过水断面,底宽1.7 m、上口宽3.3 m、高3.1 m,校核流量7.26 m3/s.工程于1977年9月15日开工,1980年12月竣工.工程砌条块石2.79万m3,浇筑混凝土0.16 万m3,挖土1.67 万m3,填土3.45万m3,投工29.32万工,为我国最大连续跨的浆砌石拱渡槽.
在红旗渡槽安全监控系统中,主要监测项目有:上下游水位、混凝土表面测缝计温度、混凝土碳化程度、渡槽沉降等.渡槽从结构上分为上部结构和下部结构,上部结构为槽身和支座,下部结构为槽墩和基础,所以渡槽的变形量监测主要分为上部结构的槽身位移监测和下部槽墩的沉降量监测.其中,采用静力水准仪来测量槽墩的沉降量,在渡槽两岸各设置一条水准路线,通过基准点对槽墩标点进行观测槽墩沉降量.红旗渡槽设12 个测点,布设位置与水平位移相同.在远离渡槽悬空跨部两端,地质条件良好且稳定处各布设沉降监测基准点1个.沉降测点上加装静力水准监测装置,实现渡槽沉降自动化监测.
3.2 模型因子选择
渡槽变形主要受水荷载、温度荷载、渡槽主体裂缝、混凝土和基岩的徐变、塑性变形等影响.考虑红旗渡槽各观测点的沉降值主要受水压、温度和时效的影响,因此,沉降的统计模型包括水压、温度和时效分量,公式为:
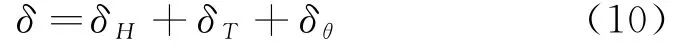
式中:δ 为位移值,δH为水压分量,δT为温度分量,δθ为时效分量.
在进行沉降变形建模分析过程中,主要考虑了如下影响因子:上下游水位平均值,水压因子取平均水位H的1~2次方;环境温度,温度因子取两处边界温度计测值T1、T2及其3次方;时效,时效因子时间的线性项θ.即输入样本的影响因子为H、H2、T1、
3.3 样本数据处理
选取红旗渡槽测点HQCJ02在2018年6月15日~2018年8月11日每天中午12:10所测得的监测资料建立预测模型,在进行异常值处理之后,一共选取50组实际观测数据.50组数据中,a 组数据集作为训练样本,用于拟合;b 组数据集作为测试样本,用于预测.a、b的取值方案分4种:方案1取a=35、b=15;方案2取a=37、b=13;方案3取a=41、b=9;方案4取a=43、b=7.
3.4 MLR模型预测效果
选取方案3(训练样本a=41、测试样本b=9)进行分析,建立基于MLR的渡槽沉降变形监控模型,用于初步判定拟合及预报的准确性.如图3所示,训练样本的拟合在数值上以及整体的趋势变化上表现良好,除去个别残差在2 mm左右,其余均分布在[-1 mm,1 mm]区间内,稳定性良好.图4表明训练样本的预测效果图显示预测误差基本分布在[-0.6 mm,0.1 mm]区间内,预测精度满足工程要求.
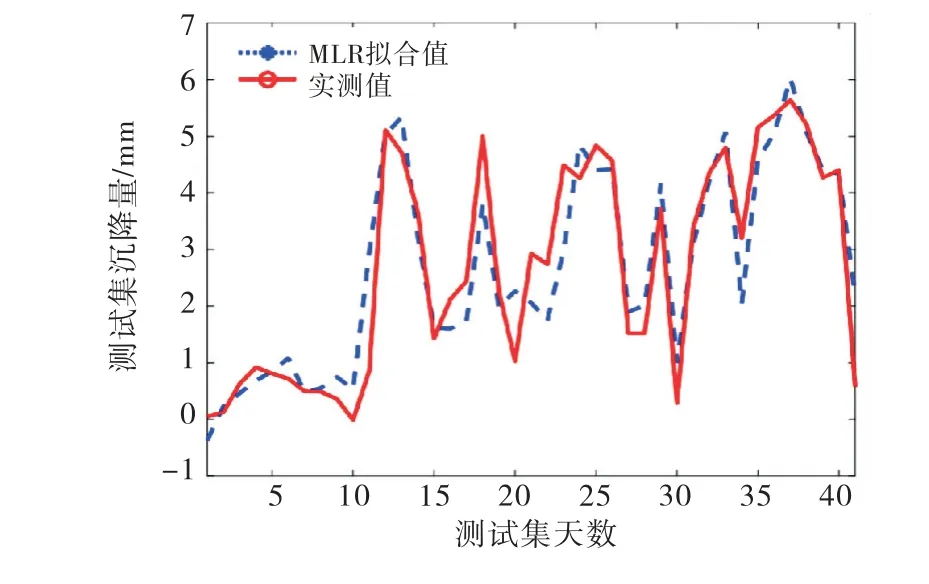
图3 HQCJ02测点沉降值拟合效果图(MLR)
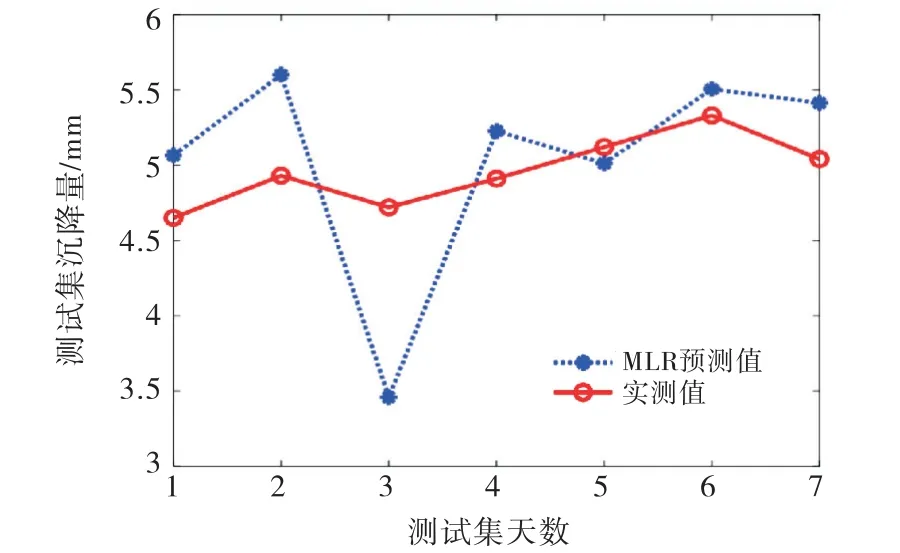
图4 HQCJ02测点沉降值预测效果图(MLR)
回归模型建立后,能否利用该模型进行有效预测,除了分析拟合曲线,还应该进行一些数理统计上的定量分析,根据2.3节给出的模型评价指标以及正态分布检验,进一步论证模型的准确性.图5表明,样本沉降变形的预测拟合值均落在图中斜率为1的直线附近,预测值和实测值的相关性良好.同时,图6显示,样本残差分布直方图与正态分布曲线十分吻合,残差通过了正态分布检验.
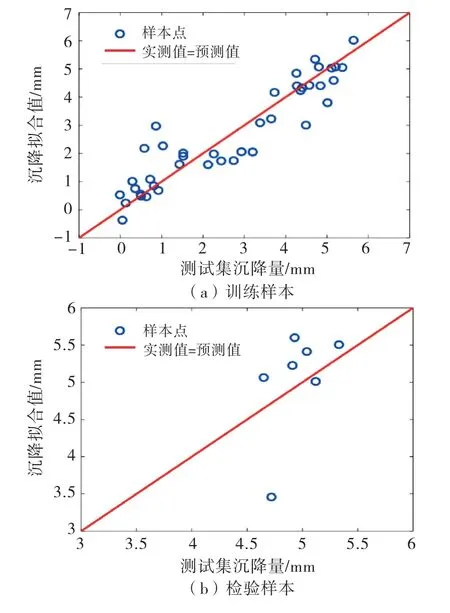
图5实测值与MLR 预测值拟合图

图6实测值与MLR 预测值残差正态分布检验
3.5 MSR模型预测效果
下面对方案3进行MSR 建模分析,与上一节采用相同的模型评价方法,沉降实测值与预测值如图7所示,实测值与预测值的拟合效果如图8所示,训练样本和检验样本的残差正态分布检验图如图9所示.
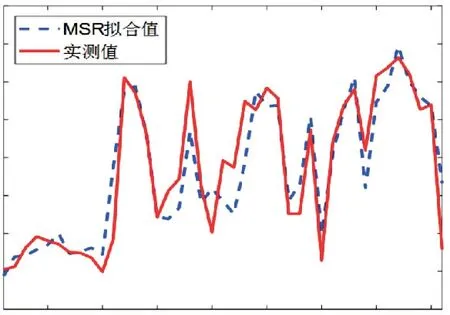
图7测点沉降值拟合及预测效果图(MSR)
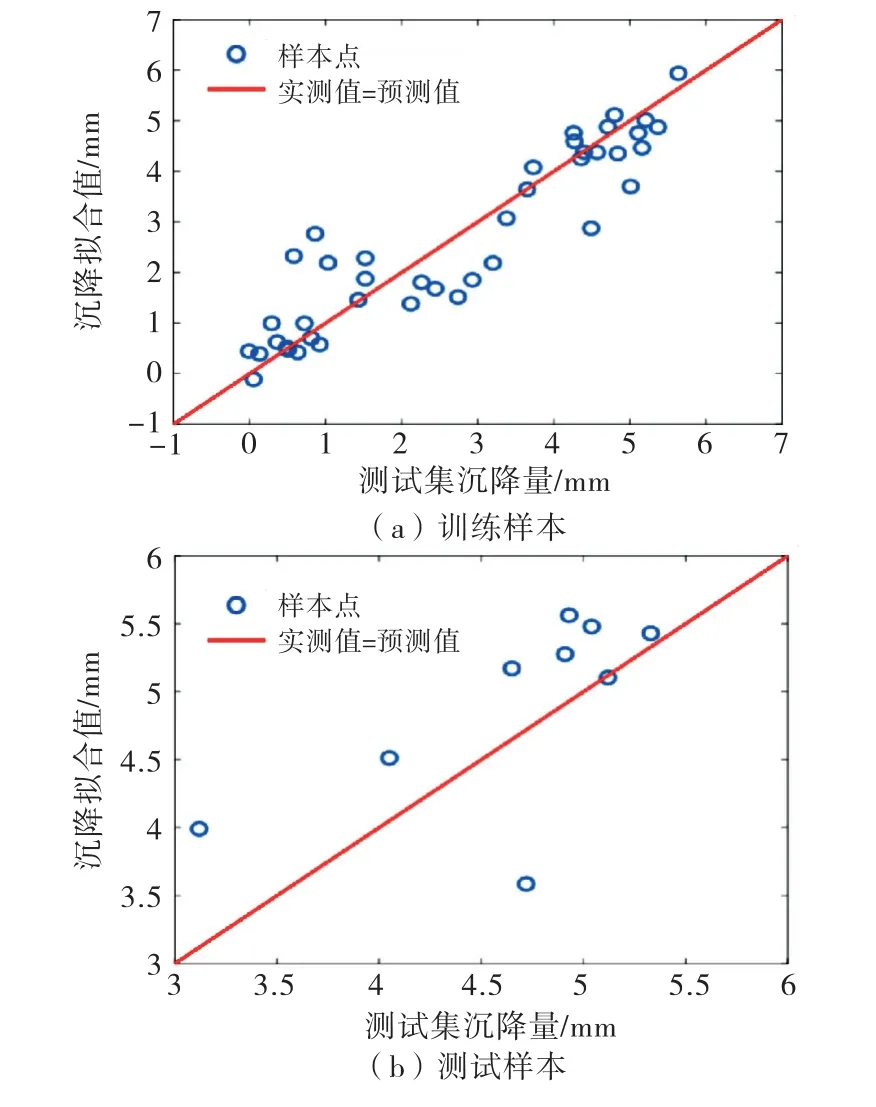
图8沉降实测值与MSR 预测值拟合图
3.6 MLR、MSR模型对比分析
两种模型的评价指标汇总见表1,将测试集以及训练集预测的最优指标用黑体加粗.
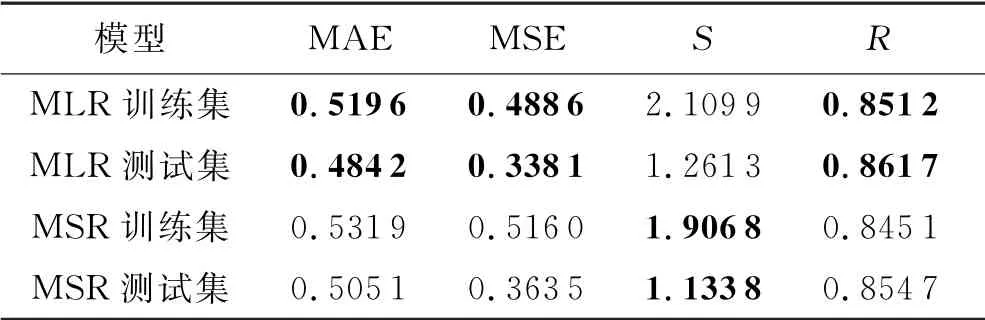
表1 MLR 和MSR 评价指标对比(a=41,b=9)
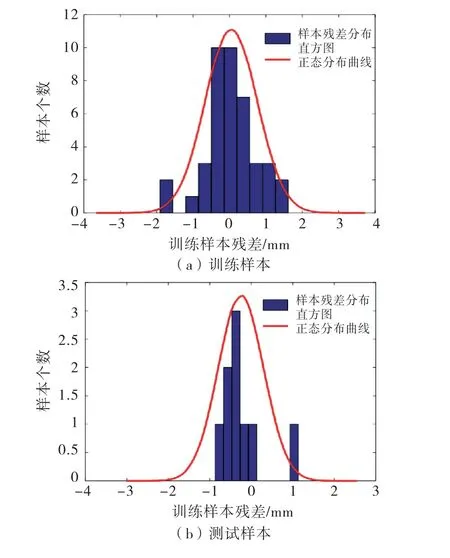
图9实测值与MSR 预测值残差正态分布检验
由表1可以看出,在训练样本数目和检验样本数目相同的情况下,不论是训练样本还是测试样本,多元线性回归模型的MAE、MSE、R指标均高于逐步回归模型,说明MLR 在沉降值的数据拟合和预测上精度占优.原因在于MSR 剔除了一些对效应量贡献不大的因子,使得回归方程达到简化.但两种模型的拟合残差波动程度几乎在同一水平,不存在明显的优劣势,均能较好拟合预测沉降值.其中,R指标计算的沉降变形预测值y0与实测值y之间的简单相关系数在0.85左右,说明沉降变形值的原因大部分可由水压分量、温度分量、时效分量解释.
3.7利用MLR拟定最佳预测天数
为了寻找最佳预测天数,将方案1到4利用MLR进行拟合和预测分析,对比结果如图10所示,并将不同方案的评价指标汇成表2,最优值加粗表示.
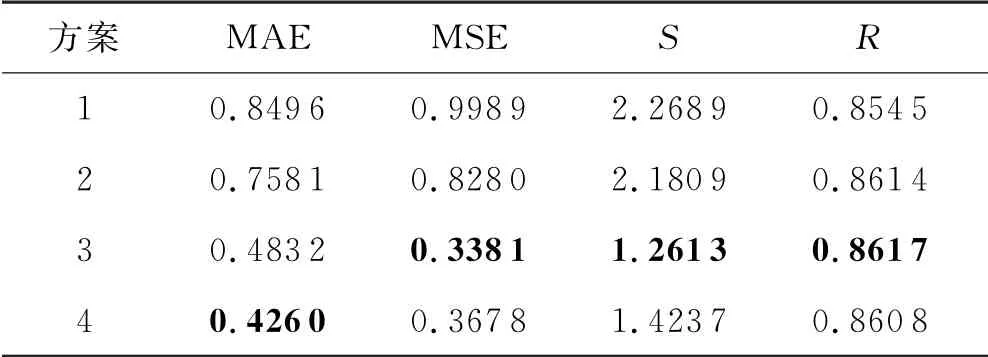
表2不同a、b取值方案对比(MLR)
从图表可以看出,当预测天数在7~15 d内变化时,模型回归的效果基本维持在一个水平;随着预测天数的减小,评价指标整体上向着更优的方向变化,当预测天数设定为9 d左右时,预测效果较好,当预测天数延长至15 d时,评价指标MAE几乎是最优值的2倍,而MSE几乎是最优值的3倍,最大绝对误差S也相应增加.可见模型的短期预测能力优于长期预测能力,说明预测天数的选择对于模型预测精度的影响一定程度上大于所选用的统计模型方法.
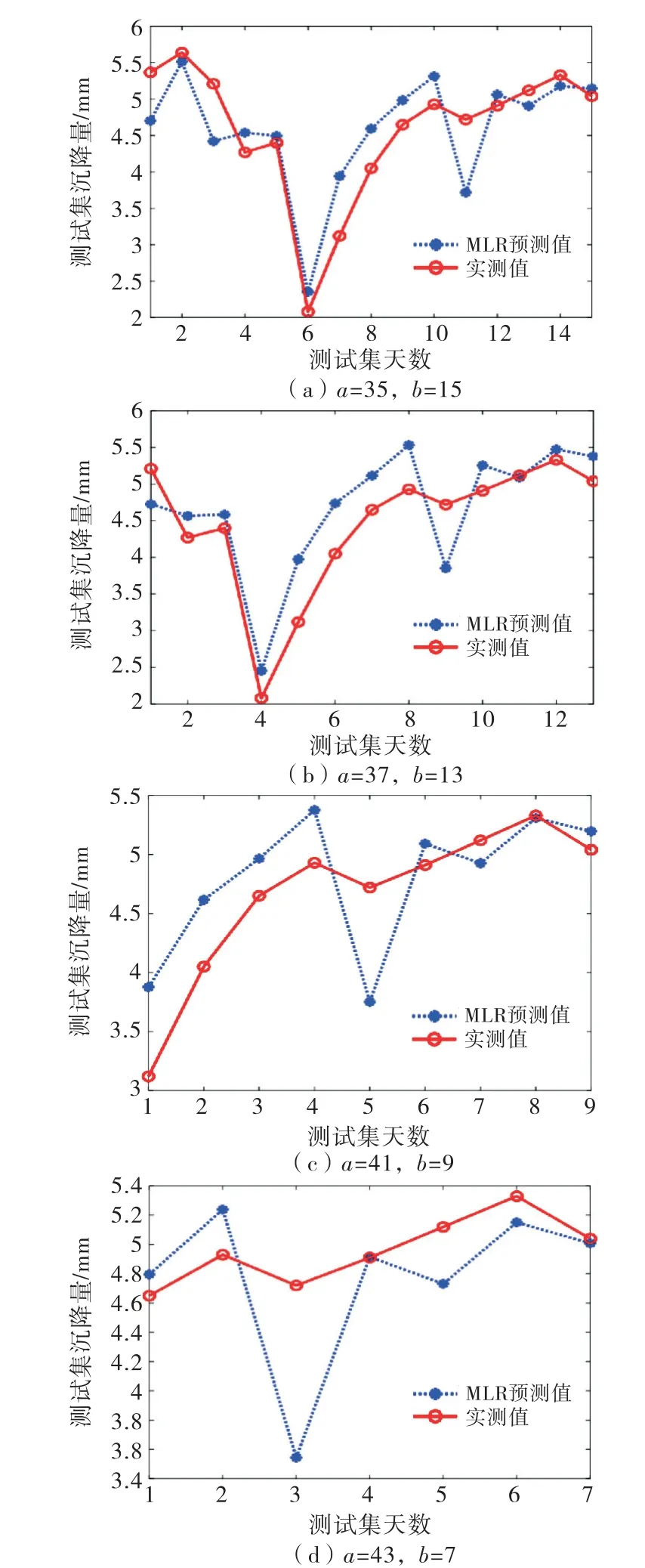
图10不同预测天数下的预测结果对比图
4 结论
针对浙江天台渡槽工程实例,选取不同数目的预测样本建立基于MLR和MSR的渡槽变形监控模型,通过分析预测样本数目不同取值方案下模型预测值与真实监测值的评价指标,探讨监控模型的预测能力.实例分析表明:1)MLR 和MSR 模型均具有良好的拟合性、适应性和预测性,可用于渡槽工程的沉降变形安全监控.2)MSR 模型由于剔除了对效应量影响不大的因子,使得回归方程更加简洁,但也略微降低了预报准确性.3)基于MLR 的渡槽变形监控模型短期预测能力优于长期预测能力.4)基于MLR 的渡槽变形监控模型的预测能力受到实测数据的直接影响,训练样本的数目以及数据的优劣程度直接决定了拟合和预测能力的好坏.采集到精准的实测数据对于合理有效预报尤为重要.
