基于Prim的局域网升级改造算法优化

贺军忠，崔俊峰

（陇南师范高等专科学校,甘肃 成县 742500）

0 引言

局域网（LAN，Local Area Network)是家庭、学校等有限空间内连接计算机的网络。为了推进校园信息化工程建设，各校会根据校园规模的扩大，对现有局域网进行升级改造与扩展，如现有局域网只连接一部分建筑内的计算机，想要将校园内所有新建筑中的计算机相互连接（原有局域网连接线路不变），也就是说，各建筑之间可以通过缆线直接/间接收发数据。为了降低升级改造与扩展的成本，要求使用最少的缆线完成校园网的升级改造与扩展。普里姆（Prim）算法是以单个起始点构成的树结构开始，向树结构逐条添加边线以生成树。因此，该过程中选择的边线始终保持连接状态。对已经生成的树结构，普里姆算法只会考虑其相邻边线。通过普里姆算法的实现方法得知，它会找出加权值最小的候选边线，并将它添加到树结构。这种过程会反复进行，直到找出最小生成树。

1 问题分析

一般情况下，校园网会把网管中心设置在校园中心位置，以方便向四周扩展，为了简化问题，把所有建筑视为二维平面上的点，为了让所有的点都能联通，并形成一颗最小生成树，通过实际测量研究，并不是最好的解决方案。最好的方案是以网管中心为中心点，在不同方向各自形成最小生成树，并保证使用最少的缆线且所有点都能联网，即任意两点之间有且只有一条通路并不能形成闭合回路。连接两个点时，只需将两点间的实际长度放缩为两边线的加权值。每条缆线只能连接两个网点，理论上两条缆线是不允许相交的，就算相交也是立体的，并不会相互连接。为了使缆线最短，最小生成树算法首选，而两种经典的最小生成树算法分别是Kruskal 算法［1］和Prim 算法［2］，由于随着校园网规模的不断扩大，最小生成树边线会不断增大，边数也会越来越多，根据Kruskal 算法的执行过程得知，边数较多时，为了减少时间复杂度，不易采用Kruskal 最小生成树算法。相反Prim 算法在执行过程中无需对边线排序，只与树中的顶点有关，因为它是每次加一个顶点［3］，对边数多时适用。只要掌握了最小生成树问题的执行过程与解法，就能满足问题的要求。解决这种问题时，最重要的是选择简单快捷的编写方法。例如，将最初给出的图1 划分成各个子网，再从得到的子图结构中求出最小生成树［4］。

2 构建基于Prim的算法模型

可以把整个校园网看作是由中心点出发，在每个方向各自形成最小生成树，如图1所示。

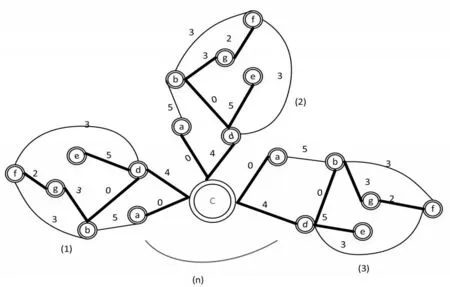
图1 扩展后校园网生成树

为了方便解答，可以将每个子网中两个建筑的间距设置为边线加权值。两个建筑之间已经有缆线连接时，就把此边线的加权值设为0。因此，各边线的加权值就相当于连接两个建筑时所需的额外现线长度。最后，利用Prim 最小生成树算法原理就能直接解决此题。其执行过程如下图2，给出各建筑位置和已安装缆线的信息，编写程序计算连接所有建筑需要增加的最短缆线长度。

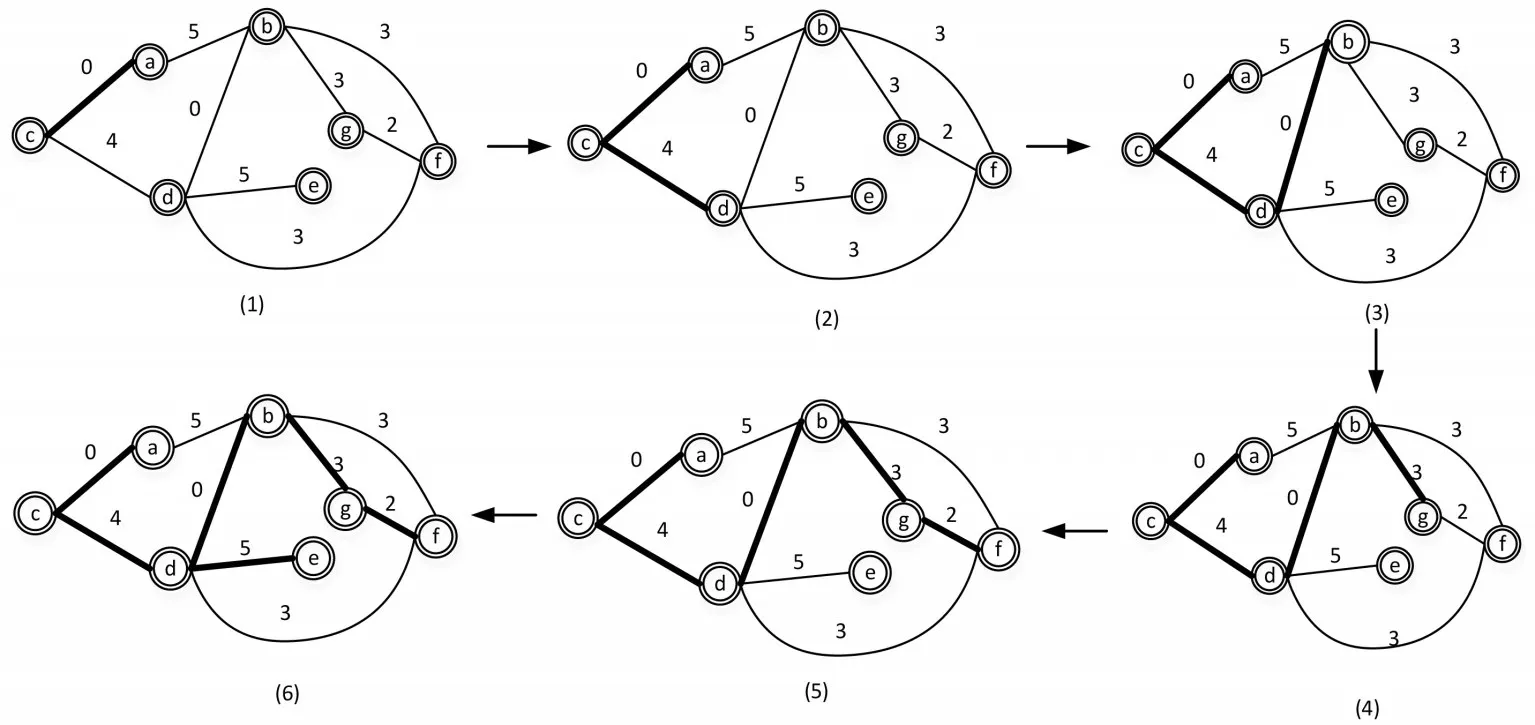
图2 生成树连接算法执行过程

在上图2 中，包含于生成树的顶点（建筑）用同心圆表示，而粗实线表示包含的边线，细实线表示没有加入最小生成树的边线，虚线为下阶段加入最小生成树的候选边线，a～f 表示顶点，0～5 表示两顶点间的加权值（距离）。由图中最小生成树的形成过程可知，以C 点为树根，添加边线权值最小的（c，a)为树的第一分技，以后每个执行阶段都会向树结构添加1条边线。图2中每个阶段都有n（n≥2）条候选边线，这些候选边线不仅会连接1 个隶属于树结构的顶点，而且也连接1 个不属于树结构的顶点。如图2（3)中的边线（a，b)，貌似属于候选边线，但连接它的两顶点都属于树结构，这样便会形成回路，所以此边线不能成为候选边线。根据Prim 算法的迭代性，不断找出加权值最小的边线，确定为候选边线，并根据最小生成树目标将它依次添加到树结构中。这种过程会反复迭代进行，直到找出最小生成树［5］。

3 基于Prim的最小生成树连接算法的优化

根据Prim 的最小生成树执行过程，连接到树结构中的顶点、边线，以及整个树结构都在不断变化，必须声明一个数组mind［t］，该数组用于保存顶点的边线最小权值和整个连接树结构，即各顶点之间的最小距离。此数组就会在每次增加新顶点时，遍历连接此顶点的各条边线，并进行更新，将最新值保存到mind［t］数组中。通过这种设计算法，就能在相应的时间复杂度O（|V|)时间内找出需要的新顶点，并添加到树结构中。要把u 和v 添加到树结构中，需各检查1次边线（u，v），所以只需对所有边线检查两次即可，因而整个时间复杂度是O（|V|2+|E|)。下面的代码表示实现这种方法的算法源代码［6-7］。为了确认各顶点连接到树结构时实际使用的边线，把使用边线的另一个顶点保存到roo［t］。连接算法的实现方法如下：

该算法首先声明顶点个数V，并定义数组mind［t］，并保存成对值（连接的顶点序号，边线加权值)到数组中。对给出的图结构，把最小生成树中的边线目录保存到变量selected 中，返回加权值之和，并判断相应顶点是否已包含到树结构中。依次保存树结构相邻边线中连接到相应顶点的最小边线的信息以及加权值之和的变量。在执行过程中，以0 号顶点为起点，依次按算法不断找出下一个顶点，将其添加到树结构的顶点集中，同时把（roo［tu］，u)加到最小生成树结构中［8］。

4 结论

通过以上论述得知，在两种经典的最小生成树算法Kruskal 和Prim 中，虽然Prim 最小生成树算法的工作原理与Kruskal算法的工作原理相同，但二者的最大差异是在执行方式上。Prim 算法是从中心点为起点，根据候选边线，不断新增连接点以构成新的树结构，不断迭代最终形成最小生成树。而Kruskal根据其算法原理，需要对所有边线先进行排序，适合边线较少时使用。由于LAN 不断扩大，边线数量不断增多，所以本研究采用Prim 算法为指导思想，所研究结构只限于有线网络。