Hellmann-改良Kratzer势Schrödinger方程的散射态解

陈文利，邢瑞芳，胡 艳

(西安培华学院智能科学与信息工程学院，陕西 西安 710125)

0 引言

在量子力学中，散射态主要研究散射离子的角分布以及散射过程中离子的各种性质的变化，是寻求理解物理系统量子信息的有效手段.在散射态理论的研究中，为获得系统的散射态解及散射相移，首要的是量子系统的解析求解，然而在解析求解过程中，径向方程中离心项的存在使得求解较为困难. 因此，基于不同的近似手段便成为解决散射问题的有效手段.例如，指数形式近似[1-2]，Pekeris型近似[3-4], 通过近似表达离心项使得径向方程转化为可解的微分方程，获得波函数的解析解.通过研究波函数在r→∞的渐进行为，获得系统的散射相移公式. 由于组合势场能提供更为广泛的应用[5-6]，在基于改良Kratzer势场的基础上加上屏蔽库仑势场构造出了更为复杂的组合势场[7].

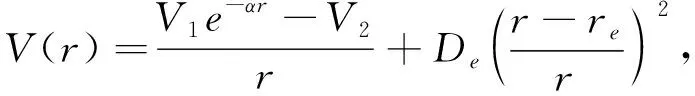
(1)

其中，V1,V2分别为Yukawa和库仑势的势场强度，α为是势屏参数，De为离解能，re为平衡键长.当势参数取不同值时，势场可退化为改良Kratzer势场、Hellmann势场和屏蔽库仑势场. 在文献[7]中,Berkdemir C 等作者求解了束缚态改良Kratzer势场薛定谔方程的束缚态解,同时,KOCAK G等和Hamzavi M等分别求解Hellmann势场薛定谔方程的束缚态解[8-9]，得到对应本征值满足的方程,然而，Hellmann-改良Kratzer势的散射态问题却较少涉及.本文拟求解其散射态解析解，得到相应的的散射态相移公式，数值求解本征值方程并和利用程序包所得本征值数据对比，最后讨论了特例的情况.

1 散射态的近似解析解

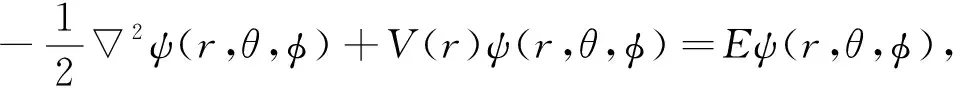
(2)

其中，E为系统能量本征值.取势函数为Hellmann-改良Kratzer势，设波函数ψ(r,θ,φ)=r-1unl(r)Ylm(θ,φ)并代入方程式(2)中，得薛定谔方程的径向方程满足方程

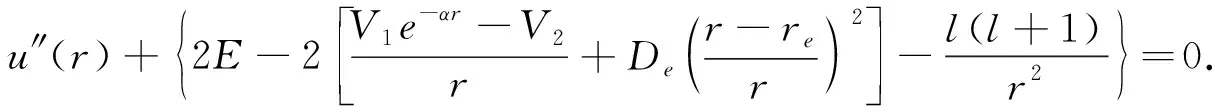
(3)

由于径向方程中离心项的存在，使得方程(3)很难解析求解，本文采用指数型的近似公式[10-11]

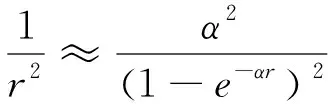
(4)

近似表示离心项，并引入无刚量变量z=1-e-αr代入方程式(3)，可得如下方程

(5)

考虑波函数的边界条件z→1(r→0),z→0(r→∞)[12]，设径向波函数为

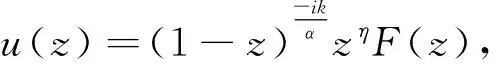
(6)

其中参数

(7)

将方程(6)代入方程(5)，化简得

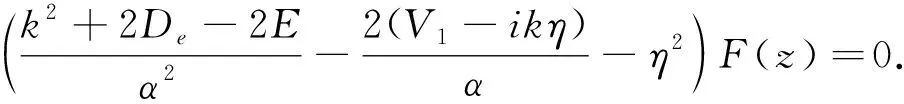
(8)

方程(8)的解恰可表示为超几何函数的表达形式

(9)

其中，符号(x)p=Γ(x+p)/Γ(x)，对应的参数a,b,c为

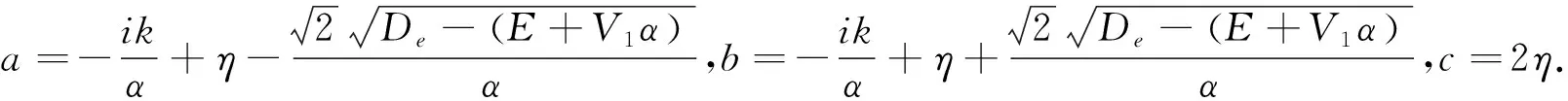
(10)

结合方程(6)和(9)，波函数可解析表示为

u(r)=Neikr(1-e-αr)η2F1(a,b,c,1-e-αr).

(11)

其中，N为归一化常数.

为了求解归一化常数和相移公式，方程(10)中参数满足以下关系：

综上所述，紫云英苷是一种具有潜在抗人卵巢癌作用的活性成分，可通过抑制HIF-1α诱导的糖酵解等通路来抑制卵巢癌细胞的增殖、促进卵巢癌细胞的凋亡，为抗卵巢癌新药的研发提供重要依据和参考。

(12)

利用超几何函数的迭代公式[13]

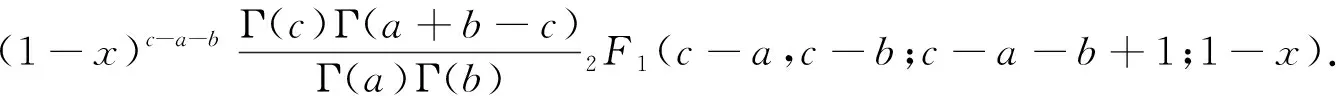
(13)

波函数的渐进行为可表示为

(14)

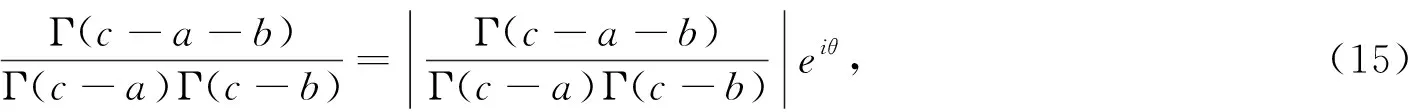
把关系式(15)代入式(14)，可得

(16)

比较式(16)和波函数的渐进行为u(r)→2sin(kr-lπ/2+δl)(r→∞)[14]，相移和归一化参数可表示为

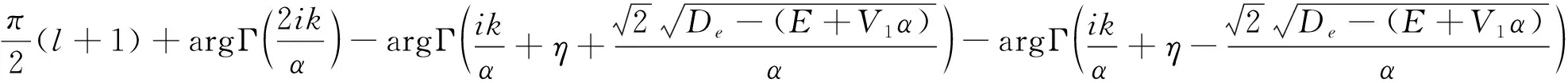
(17)

(18)

进一步讨论散射振幅及其解析性，散射振幅可表示为

(19)

上式中每一项代表l分波的散射振幅，散射振幅作为能量的函数，解析延拓到整个复平面上[15]，并研究其解析性，考虑伽马函数在整个复z平面上不为零，利用伽马函数变换公式

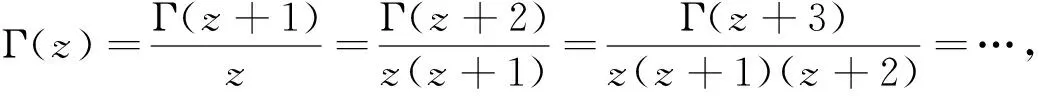
(20)

其中，z=0,-1,-2,-3…是Γ(z)的极点，因此，表示为超几何函数的波函数渐近行为也取到极点0,-1,-2,-3，…，即

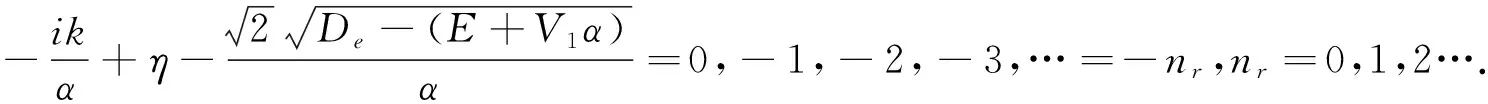
(21)

结合方程(9)、(14)，解析求解方程(21)，得到本征值满足的方程：

(22)

2 讨论

当参数De=0,V1=-1,V2=0,时，Hellmann-改良Kratzer势场退化为屏蔽库仑势场[16]，取势参数α=0.000 1数值计算本征值方程(22)和先前文献[16]所得数据进行对比,见表1，本文所得数据也较好的逼近真实值.

表1 屏蔽库仑势场对应的特征值数值解Tab.1 Numerical results of eigenvalues of screened Coulomb potential

表2 改良Kratzer势场对应的特征值数值解Tab.2 Numerical results of eigenvalues of modified Kratzer potential

当参数V1=0,V2=0，势函数退化为改良的Kratzer势场，数值求解本征值方程(22)时，可得到本征值E关于α的函数关系E(α)，计算时只需取α→0时E(α)的极限即可得到本文计算所得的改良Kratze势场本征值数值解.同时，数值求解文献[7]中方程(14)及利用程序包计算改良的Kratzer势场的本征值数据，见表2. 本文所得数据和先前结果相同，并能有效近似精确值.

对于任意l态，给定参数De=5,re=1.6，数值求解本征值方程(22)，获得的本征值数据和MATHEMATICA程序包所获结果进行对比，数据见表3. 从数据对比结果分析，本文所取得近似公式(4)能有效的近似表达离心项，当α→0,本征值所得数据较好的逼近了真实值.

表3 特征值数值解Tab.3 Numerical results of eigenvalues

3 结论

对于本文新构造的Hellmann-改良Kratzer势，利用近似公式近似表达径向方程的离心项，把含有复杂Hellmann-改良Kratzer势薛定谔方程转化为可用超几何函数表示解的微分方程，获得了径向波函数的解析解，推导出了散射态相移的公式. 利用束缚态能级在散射振幅的极点处取到的性质，得到了本征值满足的方程. 为了说明推导正确性，取定不同的参数，Hellmann-改良Kratzer势退化为改良的Kratzer势场和屏蔽库仑势场，利用本文所得数据和先前所得数据进行对比. 同时，屏蔽参数取不同值，数值计算了不同态本征值数据并和程序包所得数值对比，都验证本文本征值数据较好的逼近了真实值.