基于深度卷积神经网络的脑电图异常检测

杜云梅， 黄 帅， 梁会营*

(1. 广州商学院信息技术与工程学院， 广州 510363； 2. 广州医科大学广州市妇女儿童医疗中心， 广州 510623)

脑电图(EEG)是分析和解释大脑疾病特征的最有效的医学成像工具，有助于医生诊断意识水平、睡眠障碍、癫痫、肿瘤和病变等[1-2]，因其无创、设备成本低、时间分辨率高和使用简便等独特的优势而在探查大脑功能方面得到广泛的使用[3].

目前，临床上EEG的检测仍然依赖于有经验的医师视觉观察多通道脑电图，进而凭经验来识别其中是否包含异常的脑电波. 此方法枯燥、费时、效率低，且缺乏统一的客观标准,容易造成误判和漏判，并且评估者之间的一致性(IRA)较低[4]. 因此，需要研发自动化的EEG判读工具. 而已有对EEG进行自动检测的软件，错误率非常高[4-5].

目前有关EEG自动诊断和检测的研究方法主要分为2类：

第一类，进行启发式手工特征设计和应用的传统机器学习方法. 这类方法基于综合领域知识，对原始信号进行傅立叶变换FT、小波变换WT或希尔伯特变换HT等基变换，从变换分解出来的系数中提取时间、频率或能量等方面的特征，最后用SVM、KNN和朴素贝叶斯等传统机器学习方法对脑电信号进行分类识别. 此类方法过程主观，计算费时[6].

第二类，应用深度学习进行自动特征检测、分层特征提取. 这类方法不进行手工方式的特征提取和选择，而是利用网络自动地学习特征并进行分类识别. 其中大部分研究采用浅层的网络结构，不能充分提取EEG更高层的特征[7-8]；部分研究采用小样本量数据集，深度学习模型的训练效果有限[2,6，9-10].

为了解决上述问题，本研究首先构造一个较大的EEG数据集，用于模型训练与测试；其次建立深度的卷积神经网络，以充分学习EEG信号数据的高层特征，从而形成具有较高准确率的EEG自动检测模型.

1 数据

1.1 数据重构

头皮表面记录的脑电信号一般只有几十至几百微伏(μV)，需要通过几百万倍的放大才能显现，EEG仪器的核心就是放大器，一个放大器构成一个通道，放大器之间的连接有2种导联方式，参考导联反映的是单个记录点的绝对电位，双极导联记录的是两点之间的电位差[11]. 电极的安放位置一般参考国际脑电图学会建议的10-20系统或美国脑电图协会的10%系统(图1)[12].

本研究采集了多个异构的EEG数据集[2,12-14]，这些数据集来自不同机构，记录数据的设备和标准都有所差异，将它们进行组合来训练模型，能提高模型的泛化能力，降低过拟合的可能. 由于各个数据集的通道数不同(20～40个)，采样频率也不同(250～512 Hz)，电极的导联方式也不同，所以，综合数据的分布以及转换的可能性，本研究通过插值或降采样将数据进行重构，即把频率统一为256 Hz，将通道数与导联方式统一映射为22通道双极导联(表1). 具体方法是:首先，从EEG源文件读取信号数据对应的通道名称(表2)；然后，根据通道名称所代表的导联方式以及各通道名称在图1中的电极位置确定通道映射关系(表3)；最后，根据表3的映射关系，将32通道参考导联数据重构为22通道双极导联数据.

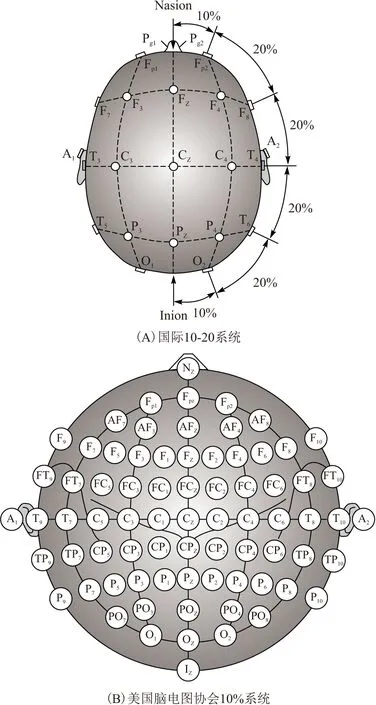
图1 电极名称和位置[12]

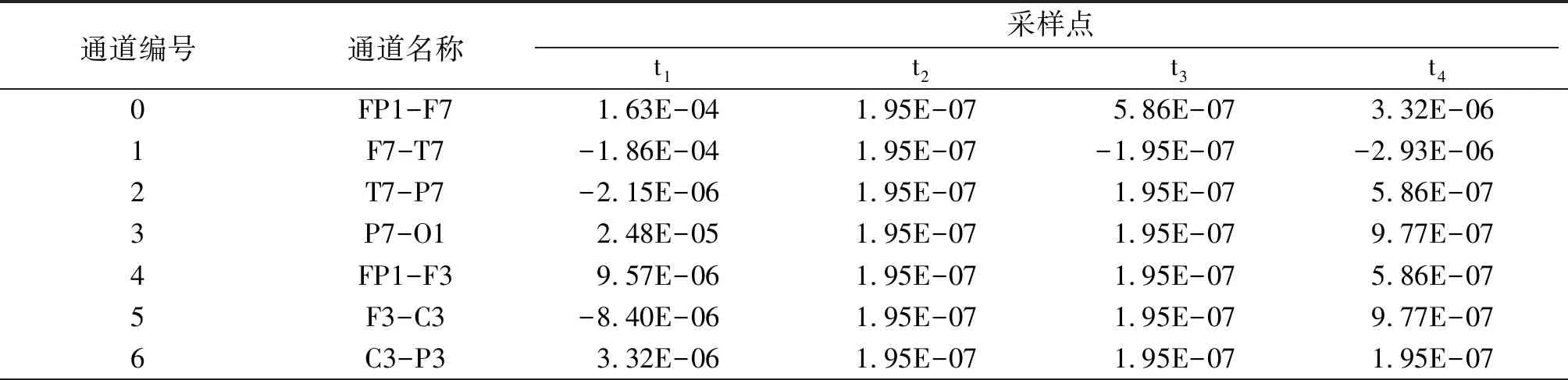
表1 数据示例:22通道双极导联

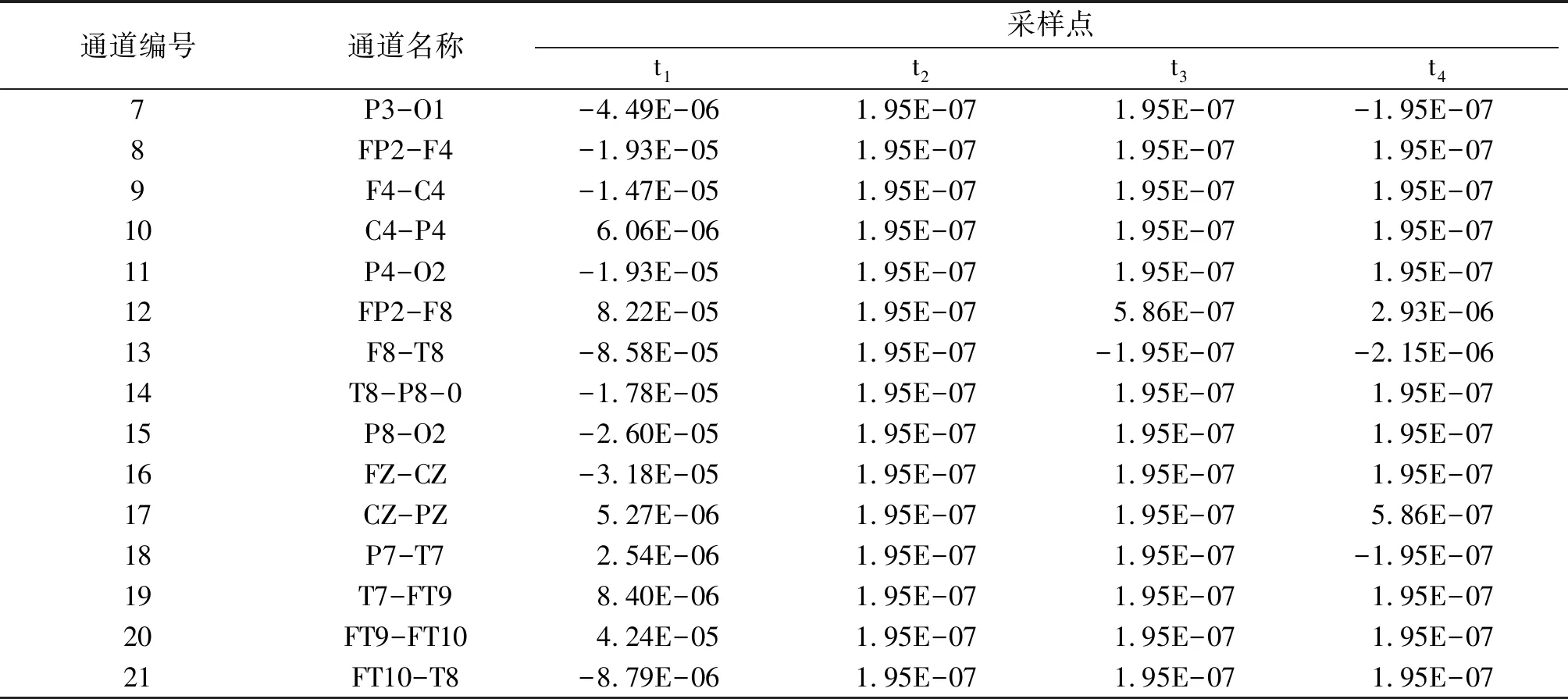
续表1

注:如果EEG的采样频率是256 Hz，那么每秒就有256个采样点，这里只列出了其中4个采样点的数据作为示例. 表2同.

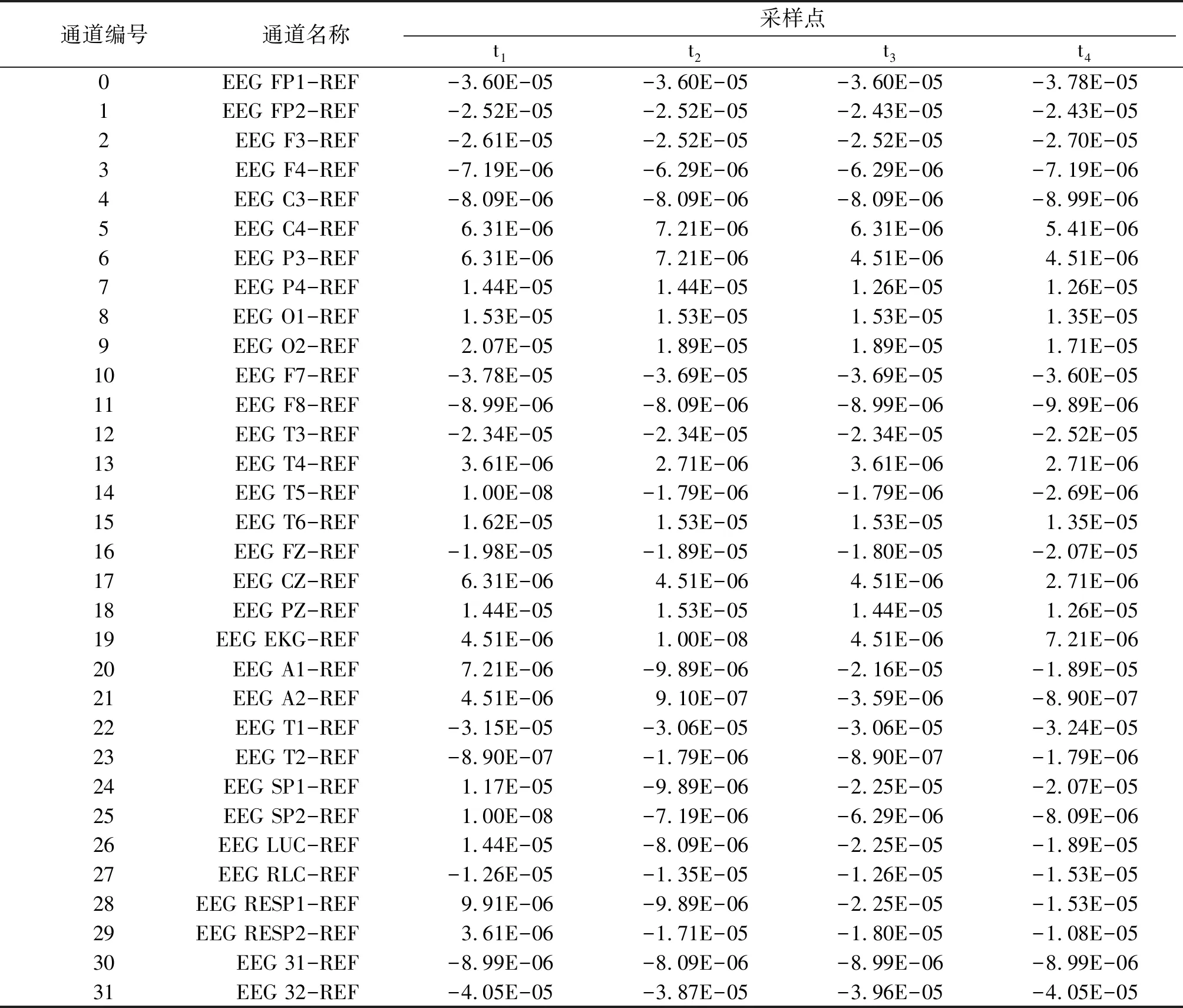
表2 数据示例:32通道参考导联

1.2 数据预处理

首先，将重构得到的二维结构的数据经过降噪，消除肌肉、眼睛、心脏活动、线路和电极等干扰[3].

然后，将降噪后的数据进一步处理为一维时间序列. 对EEG信号的每个时间点ti，把22个通道值叠加取平均作为这个时间点的样本值Si，计算公式如下：

(1)

其中，j{0,1,2,…,21}表示22个通道的编号，Cj表示双极导联中的通道. 如表1的二维数据经此步骤转换为表4的一维结构.

表4 数据示例:二维数据转换成一维时间序列

Table 4 The data example:converting two-dimensional data into one-dimensional time series

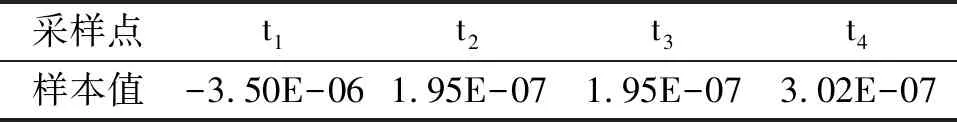
采样点t1t2t3t4样本值-3.50E-061.95E-071.95E-073.02E-07

最后，对一维数据进行归一化，并划分成长度为2 s的EEG片段,每个片段有512个数据点,只包含一种类型(正常/异常)的脑电信号. 为了获得更多数据，本研究没有做精确切分，而是以2 s的时间窗、1 s的滑动步长，沿时间方向平移，截取EEG片段，去除边界上不足2 s的情况.

全部数据集经上述划分共产生130 738个EEG信号片段，每个片段分别标注标签(正常/异常)，信号与标签同步乱序之后，切分出没有交集的训练集(118 716个样本)和测试集(12 022个样本).

2 一维CNN深层模型

本研究使用一维卷积神经网络(1D CNN)来完成EEG的特征学习与分类任务. 1D CNN常用于时序数据建模，以在模型训练过程中发现时序数据的局部特征;可有效地从整体数据集中较短的(固定长度)片段中获得感兴趣特征，且该特性在该数据片段中的位置不具有高度相关性[15].

2.1 一维CNN深层模型体系结构

深度学习网络的深度对最后的分类和识别的效果有着很大的影响，本研究搭建了31层的深度卷积神经网络. 由于存在梯度消失和梯度爆炸的问题[16]，深的网络很难训练，因此，本研究采用了残差网络架构中的快捷连接[16]，以使深层网络更容易优化训练. 模型中基本残差模块(Unit)的结构如图2所示.

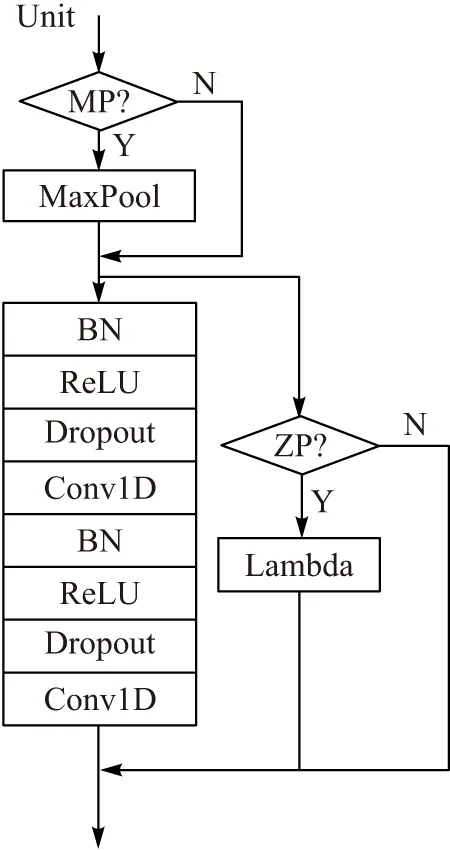
图2 残差模块的结构

Unit主路径上包含2层一维卷积操作Covn1D，卷积之前都安排了批处理归一化BN、校正线性激活ReLU和衰减Dropout. 图2中MP表示“最大池化操作”，ZP代表“进行零扩展”.

以基本模块Unit为单位搭建的整体网络架构如图3所示. 为了匹配数据尺寸与模型深度，本模型没有在每个残差块都进行池化操作，而是间隔进行，含MP的Unit块代表需进行最大池化操作(MaxPool);在过滤器个数发生变化时，快捷连接上要进行零扩展以保持张量形状的一致，含ZP的Unit块代表需进行零扩展(Lambda). 过滤器的长度保持不变，过滤器个数从32个开始，每4个Unit残差块翻一倍，变化过程如括号中的数字所示. 512维的输入数据经过7次池化(MP)后变成4维，展平后经全连接层应用SoftMax激活，最后给出每个EEG片段的正常或异常分类结果. 整个网络包含1个独立卷积层和15个残差块Unit，总共有31个卷积层.

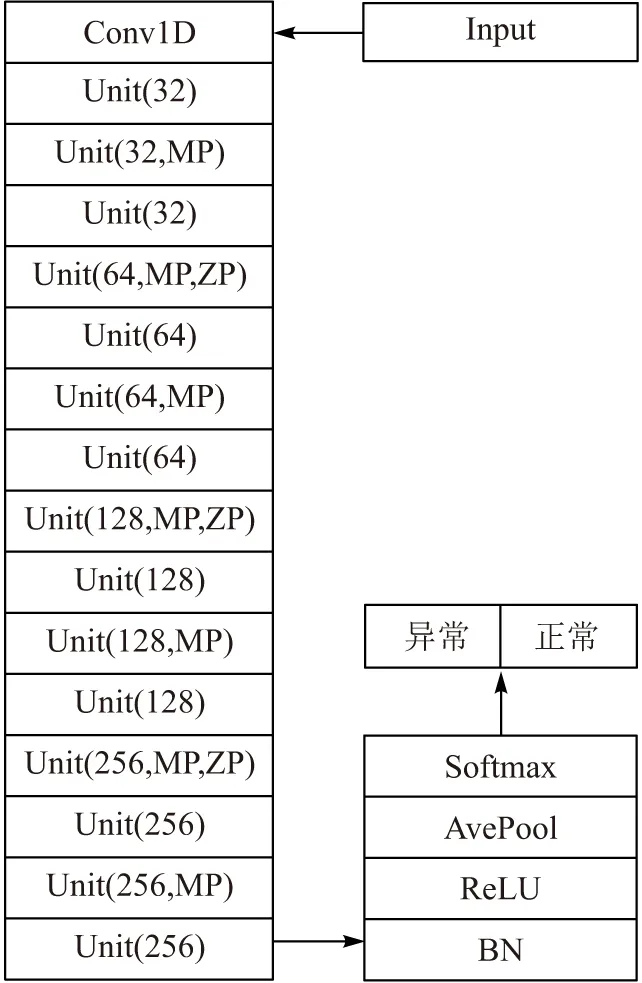
图3 整体网络结构

2.2 模型实现

网络模型采用Keras深度学习框架实现，并从头开始训练. 经过反复试探，模型最终使用“categori-cal_crossentropy”目标函数和“Adam”优化器，学习率从0.001开始，并在验证损失停止改善时将学习率降低10倍，Batch-size设为256，Epoch设为200.

3 实验结果与分析

用数据处理得到的训练集对本研究得到的一维深度CNN模型进行训练，用测试集对训练结果进行评估，以找到最优的预测模型.

3.1 训练、实验与评价指标

为了找到合适的过滤器的长度，本研究开展了几个对比实验：保持训练集、测试集、模型结构(图3)与其他参数不变，分别用不同长度(f=3,8,10,16)的过滤器进行实验，测试结果显示f=10的性能相对较好(表5).

表5 不同过滤器长度下的测试正确率

Table 5 The test accuracy under different filter lengths %

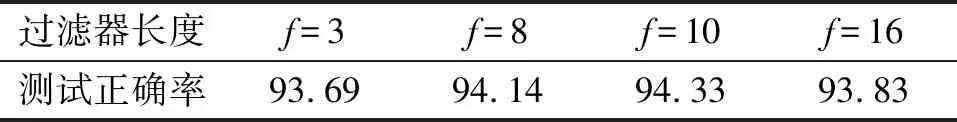
过滤器长度f=3f=8f=10f=16测试正确率93.6994.1494.3393.83

训练过程中构造了2个评价指标RMSE和AUC：

(1)RMSE用于衡量预测值ypred与真值ytrue之间的偏差：

(2)

(2)AUC为ROC曲线所覆盖的区域面积，该值越大，表示分类器分类效果越好. 采用回调函数实现，每个Epoch计算一次.

模型训练中AUC与RMSE的变化过程如图4所示. 训练30代之后验证集上的AUC稳定在0.999 3左右，RMSE稳定在0.056 9左右.

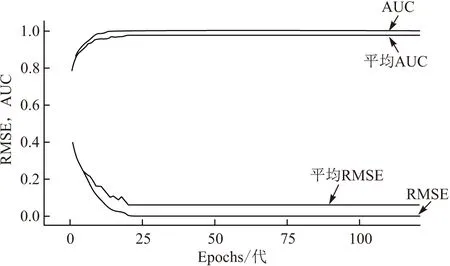
图4 训练过程中RMSE和AUC随Epoch的变化

Figure 4 The changes of RMSE and AUC with Epoch during training

3.2 测试结果与分析

用上述训练好的模型在独立测试集上进行预测，由预测结果的混淆矩阵(表6)可以看出：96%的异常脑电图信号被正确分类为异常，93%的正常脑电图信号被正确分类为正常.

表6 测试集上的混淆矩阵

本文的目标是异常检测，要在保证精确率的基础上提升模型召回率. 由模型主要的分类评价指标(表7)可知:异常脑电图的召回率高于精确率，即查全率高于查准率，测试结果与本文期望一致.

表7 每个类别主要分类指标的文本报告

以上测试结果表明在EEG信号通道均值上使用1D CNN模型的分类性能比较好，究其原因，主要是以下3个方面的设计：

第一，多个异构数据源的重构及预处理，增大了训练与测试数据量，不仅能提高训练与分类效果，还能提高模型的泛化能力与鲁棒性，经过训练的模型在完全独立的测试集上表现依然较好.

第二，取通道均值的数据处理方法，因为大脑神经元异常放电，通常会导致相邻的头皮检测点上都有异常的电位信号，通过取平均值，一定程度上强化了异常放电的程度，有些相关研究[4-5]只是取一个通道上的值进行学习和分类，就失去了相邻检查点的同步变化信息.

第三，使用一维深度卷积神经网络来进行自动学习化特征，学习到的主要是信号在时域上的动态变化，即头皮检测点上电位随时间的变化特征，从而弱化了不同EEG基线之间的差异. 脑电信号的个体差异比较大，特别是儿童脑电图和成人脑电图有很大的区别，本研究采用的数据集中包含将近三分之一的儿童EEG和三分之二的成人EEG，因为模型弱化了基线差异，所以实验中没有对年龄段进行区分，仅使用时域方面的特征进行正常异常检测已能取得较好的分类正确率.

3.3 对比实验与分析

为了进一步验证神经网络的深度对模型性能的影响，本文从2个方面进行了研究:

首先，与已有研究成果进行对比. 选取了2个同样采用1D CNN对EEG进行分类的研究[6,17]与本文的31层CNN模型(图2，图3)进行对比. 从模型准确率来看，本文的31层网络的准确率高于文献[17]的5层模型和文献[6]的13层模型(表8).

其次，设计对照实验进行验证. 上述3个研究所使用的数据集、处理方法和参数都不相同，不能充分说明在EEG分类应用背景下深层模型与浅层模型的性能优劣，为了进一步地进行验证，本研究另外设计了不同深度的CNN模型(图5)，与本文的31层CNN模型(图2、图3)进行对照. 图5A是5层卷积模型，卷积步长为2，“×4”表示循环4次；图5B是15层卷积模型，卷积步长为1，每两层卷积增加1个池化层；图中“@”后的数字表示每次卷积操作的过滤器个数. 对照模型的层次不是很深，所以没有引入快捷连接. 用相同的数据集、卷积核和目标函数等参数进行模型训练，并用相同的测试集进行模型验证. 另外，也设计了比31层更深的模型进行实验，发现过拟合的现象比较明显，所以没有将其引入对比实验.

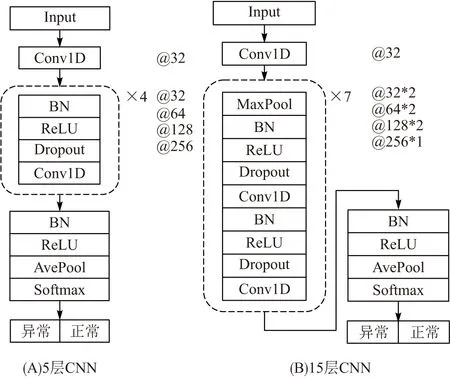
图5 对照实验的模型结构

由实验结果(表8)可知：模型的深度与最终分类正确率存在正相关的关系，随着深度的增加，准确率有所提升.

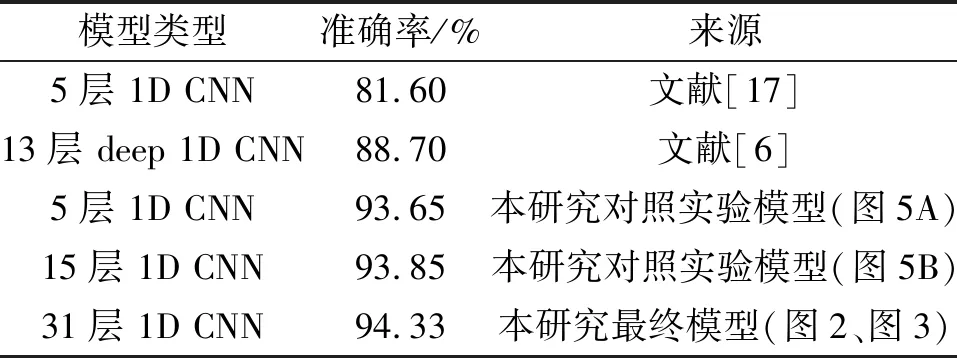
表8 5个模型的分类正确率

4 结语

本研究对多源异构的脑电数据进行重构和预处理，建立了31层一维卷积神经网络模型，自动提取特征进行脑电信号异常检测. 分析结果表明：采用较深的卷积神经网络能取得较好的分类准确率.

经过重构与预处理的EEG数据，在31层 1D CNN模型上进行训练和测试，结果达到了94.33%的分类正确率和0.999 3的AUC. 可见只从时域上用一维深度CNN能对脑电信号进行高效的分类识别，可用于临床辅助诊疗. 后续研究可考虑将时域特征与EEG通道空间关系特征相结合，以进一步提高对脑电信号进行自动检测的正确率.