5,15-二(五氟苯基)-10-(2-氨基苯基)金属咔咯的二阶非线性光学性质

王 健， 应 晓*， 刘海洋

(1. 华南理工大学应用物理系， 广州 510641; 2. 华南理工大学化学系∥广东省燃料电池重点实验室， 广州 510641)

非线性光学(NLO)材料具有独特的光学性质，可被应用于光学信号处理[1]、数据存储[2]、光学器件制造[3]等领域. 常见的NLO材料包括无机材料、有机材料和有机金属材料[4-6]. 与无机材料相比，有机NLO材料具有较大非线性光学系数、光学响应时间短、较高损伤阈值和易于进行分子设计等优点[7-8]，因此受到广泛关注. 卟啉类化合物由于具有π共轭大环结构和易于进行分子修饰等特点，因此可作为优良的NLO材料[9]. SEN等[10]设计并合成了一系列供-受体卟啉及金属配位化合物分子，发现引入金属离子可显著增强自由卟啉分子的二阶NLO响应，开壳层CuII(d9)比闭壳层ZnII(d10)影响更为明显. HU等[11]设计了一系列给体-桥-受体锌卟啉化合物，通过理论计算探究了取代基位置、π桥长度等因素对锌卟啉二阶NLO性质的影响.

咔咯是一类具有18π电子结构的类卟啉结构化合物，由于2个吡咯环直接相连导致碳原子缺失，使其具有本征非中心对称结构[12]. 基于这种独特的结构特点，可通过分子设计与修饰，使其成为优良的二阶NLO材料. 本课题组的前期研究[13]通过咔咯分子外围取代基的修饰，显著增强了咔咯分子二阶NLO响应，通过超瑞利散射(HRS)实验，在波长为1 500 nm的光辐照作用下，二阶NLO系数(β1500nm)可达354×10-30esu. SANKAR等[14]合成了金属铜、镍咔咯二聚体并通过HRS实验测量了1 064 nm波长作用下金属铜、镍咔咯二聚体的二阶NLO性质，镍咔咯二聚体具有最大的二阶NLO系数(β1 064 nm=43.1×10-30esu). 尽管咔咯化合物NLO性质已有上述实验探究，但有关金属咔咯二阶NLO性质的理论研究却少有报道[15]. 为了探究中心金属离子对咔咯二阶NLO性质的影响，本文以5,15-二(五氟苯基)-10-(2-氨基苯基)(F10Cor)为母体，通过密度泛函理论方法系统研究不同电子组态的金属离子(MnⅢ：d4,CuⅢ:d8,GaⅢ:d10)对咔咯配合物二阶NLO性质的影响，为新型咔咯化合物二阶NLO材料的分子设计提供理论依据.

1 计算方法

分子与外电场E相互作用，其感应极化强度P可表示为[16-17]：

P=P0+αE+βE2+γE3+…,

(1)

其中，α为分子极化率;β为第一超极化率(即二阶NLO系数). 分子的固有偶极矩μ0、静态极化率α0和静态第一超极化率β0的计算公式：

(2)

(3)

(4)

(5)

(6)

其中，βi代表沿坐标轴方向的分量;Δα表示分子的各项异性值；极化率α0为二阶张量；β0为三阶张量. 采用密度泛函理论(DFT)B3LYP[18-19]方法，非金属原子采用6-31G(d)基组[20]，而金属原子选用考虑了Stuggart赝势的SDD基组[21]，进行分子结构的几何优化，所有分子结构均未设置对称性限制. 然后在相同计算水平下进行振动频率的计算，证实优化后的几何结构均为不含虚频的稳定结构. 注意B3LYP由于其低HF成份(20%)并不适用于共轭体系的激发态性质计算，而CAM-B3LYP是一种非常适于共轭大分子激发态计算的范围分离泛函[22-23]. 此外，弥散函数对于偶极矩与超极化率的计算具有重要影响[24]. 因此，运用含时密度泛函理论(TD-DFT)，结合态求和(SOS)方法[25]在CAM-B3LYP/aug-cc-pVDZ[26-28]下计算分子的极化率α0和第一超极化率β0. 通过TD-DFT计算，可模拟其电子吸收光谱，分析激发态跃迁性质. 最后，运用波函数分析方法，分析体系中激发态对第一超极化率的贡献. 所有计算均通过Gaussian09程序[29]完成，使用Multiwfn程序[30]进行波函数分析，分子轨道图由VMD软件绘制[31].

2 结果与讨论

2.1 几何结构与电子光谱

F10Cor及金属配位化合物的结构如图1所示，首先进行几何结构优化，咔咯分子的几何结构参数如表1所示. 在F10Cor分子中2个吡咯环直接相连形成的二面角角度最大(∠C2-1-19-18=17.624°)，可知F10Cor中咔咯大环呈现非平面结构，而当引入中心金属离子后，配合物中的二面角∠C2-1-19-18显著减小，这种现象表明中心金属离子可显著增强配合物大环结构的平面性. 此外，F10Cor分子直接连接2个吡咯的碳原子C1和C19，其键长为0.142 5 nm，而金属配合物中C1—C19键长改变量(0.000 2～0.002 9 nm)很小，说明中心金属离子对咔咯空腔结构的影响不大. 另外，配位化合物的金属离子与氮原子形成配位键的键长(约0.190～0.192 nm)变化也不大，且与文献[32]中的计算结果基本吻合.

图1 5,15-二(五氟苯基)-10-(2-氨基苯基)咔咯(F10Cor)及金属配位化合物(F10CorM, M=Mn、Cu、Ga) 的分子结构

Figure1 The molecular structures of 5,15-bis(pentafluorophenyl)-10-(2-aminophenyl) corrole (F10Cor) and metal corrole (Mn, Cu, Ga) complexes

表1 F10Cor 和 F10CorM(M =Mn,Cu,Ga)的几何结构参数及Mulliken电荷

文献[33]～[34]报道了CAM-B3LYP泛函可适用于卟啉和咔咯化合物激发态性质的计算，当用于咔咯电子吸收光谱的计算时，其计算值与实验值比较接近. 因此，基于几何优化的结构，本文应用含时密度泛函理论在CAM-B3LYP/aug-cc-pVDZ水平模拟了电子吸收光谱，计算出最大吸收波长、振子强度、跃迁能和跃迁形式列于表2. F10Cor气相下的最大吸收波长(max=370 nm)与实验值(415 nm)[13]相差偏大, 但考虑溶剂等因素的影响，计算结果尚在误差范围内[35]. 对于金属配位化合物，金属离子的引入使F10CorMn和F10CorCu的max分别蓝移了21、23 nm，而F10CorGa的max蓝移程度较小(8 nm). 图2分别为F10Cor和F10CorM(M=Mn、Cu、Ga)的前线分子轨道图. F10Cor的max来自咔咯大环上HOMO-1到LUMO+1和HOMO到LUMO的π→π*跃迁，属于分子内电荷转移. 而引入金属离子后，F10CorMn的max主要来自β-HOMO到β-LUMO+5的π→π*跃迁，属于配体内电荷转移(ILCT)，F10CorCu的max主要来自β-HOMO到β-LUMO+2的π→π*跃迁，可归属为ILCT，Mn(Ⅲ)和 Cu(Ⅲ) 使max相应的轨道跃迁形式发生较大变化，其跃迁能增大，相应的max出现显著蓝移. F10CorGa的max来自咔咯大环上HOMO-1到LUMO+1和HOMO到LUMO的π→π*跃迁，属于ILCT，这与F10Cor最大吸收跃迁形式相似，可知Ga(Ⅲ)对最大吸收波长的电子激发性质影响并不大，仅稍微增大了跃迁能，相应的max出现微小蓝移. 综上分析可得，中心金属离子对咔咯配位化合物的电子吸收光谱产生了不同程度的影响，Mn(Ⅲ)和Cu(Ⅲ)对体系max均有显著影响，而Ga(Ⅲ)未能显著改变体系max的跃迁性质.

表2 计算所得咔咯最大吸收波长(max)、振子强度(f)、基态与激发态偶极矩之差(Δμ)、跃迁能(ΔE)和主要跃迁形式

Table 2 The calculated maximum absorption wavelength (max/nm), oscillator strengths (f), difference in dipole moments between ground and excited state(Δμ), transition energy (ΔE) and major transition forms of corroles

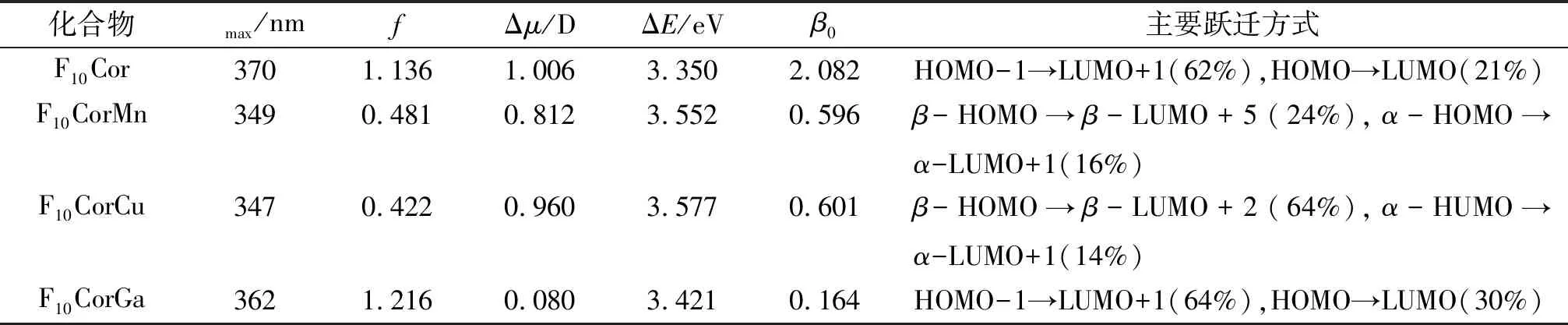
注：β0表示双能级模型计算值(×10-30esu)，α和β指分子轨道的α和β自旋态.

图2 F10Cor及金属配位化合物的前线分子轨道

2.2 偶极矩与极化率

基于B3LYP/6-31G(d)/SDD计算所得几何优化结构，在CAM-B3LYP/aug-cc-pVDZ水平上计算偶极矩. 由F10Cor及F10CorMn、F10CorCu、F10CorGa基态偶极矩μ0的变化(表3)可知，中心金属离子的引入显著减小了配位化合物基态偶极矩的大小. F10Cor在x、y轴分量μx、μy对总偶极矩μ0的贡献较大，其中μy占主导. 由偶极矩分量的变化趋势可知，与F10Cor相比，配位化合物中心金属离子主要减小了μx、μy，同时改变了分量μz的方向而并未显著改变其大小，配位化合物分子基态偶极矩μ0(F10CorCu)>μ0(F10CorGa)>μ0(F10CorMn). 咔咯及其配位化合物的Mulliken电荷分布(表1)表明，金属离子与咔咯配体间存在不同程度的电荷转移，因而配位化合物基态偶极矩表现出一定的差异. 由表4可知，μx、μy对平均极化率α0的贡献占主导，μz对α0贡献极小. F10Cor的平均极化率和极化率分量均略高于F10CorM的情况，可见中心金属离子未能增大配位化合物的极化率. 金属配合物的平均极化率α0(F10CorGa)>α0(F10CorCu)>α0(F10CorMn)，当受到入射波长为1 907 nm的光照射作用时，咔咯及其配位化合物的动态极化率均增大.

表3 咔咯的基态偶极矩(μ0)及其分量

Table 3 The ground state dipole moments (μ0) and components of corroles

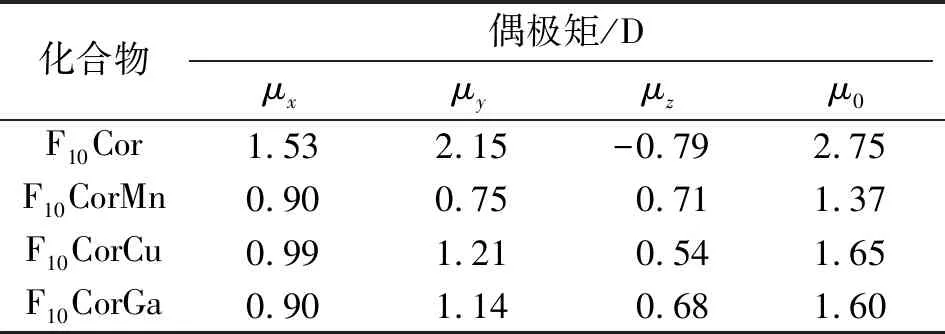
化合物偶极矩/Dμxμyμzμ0F10Cor1.532.15-0.792.75F10CorMn0.900.750.711.37F10CorCu0.991.210.541.65F10CorGa0.901.140.681.60

表4 咔咯的静态极化率α0及其分量

注：括号中的数据是动态极化率α1907 nm.

2.3 非线性光学性质

分子的静态第一超极化率也称为无外电场作用下的二阶非线性光学系数，通过SOS方法在CAM-B3LYP/aug-cc-pVDZ水平计算静态第一超极化率β0，体系激发态数目与β0的收敛关系见图3. 随着激发态数目的增加，β0基本趋于收敛. F10Cor和F10CorM的β0及分量(βx、βy、βz)列于表5. 当中心金属离子进入咔咯空腔后，配位化合物的β0变化趋势不同. 由表5可知，F10CorCu表现出最强二阶NLO响应，而F10CorMn和F10CorGa的β0显著减小，进一步分析β0分量可知，F10Cor的βy对β0有显著贡献. 当引入中心金属离子后，配位化合物的βy分量仍然是主要贡献分量. 值得注意的是，Cu(Ⅲ)显著增大了主要贡献分量βy, 促使F10CorCu二阶NLO响应增强. 而与F10Cor相比，F10CorMn、F10CorGa的βx、βy、βz均大幅减小，F10CorMn、F10CorGa二阶NLO响应的减弱，可见中心金属离子的引入改变了咔咯配位化合物第一超极化率分量. 通过Coupled-Perturbed Kohn-Sham(CPKS)方法也可得到咔咯分子静态第一超极化率β0(CPKS)，CPKS方法与SOS方法计算的β0基本吻合(表5)，所得β0大小顺序一致，这进一步说明SOS的计算值是可靠的. 由计算结果可知，咔咯分子静态二阶NLO系数显著大于文献[10]报道的5,10,15,20-四(五氟苯基)铜卟啉配位化合物(3.9×10-30esu)和文献[36]报道的非线性光学材料磷酸二氢钾(KDP)( 2.745×10-30esu)，YING等[13]采用超瑞利散射方法测得5,10,15-三(五氟苯基)咔咯二阶NLO系数可达50×10-30esu，以上结果表明咔咯化合物具有较强的二阶NLO响应，可为二阶NLO分子设计提供良好的平台.

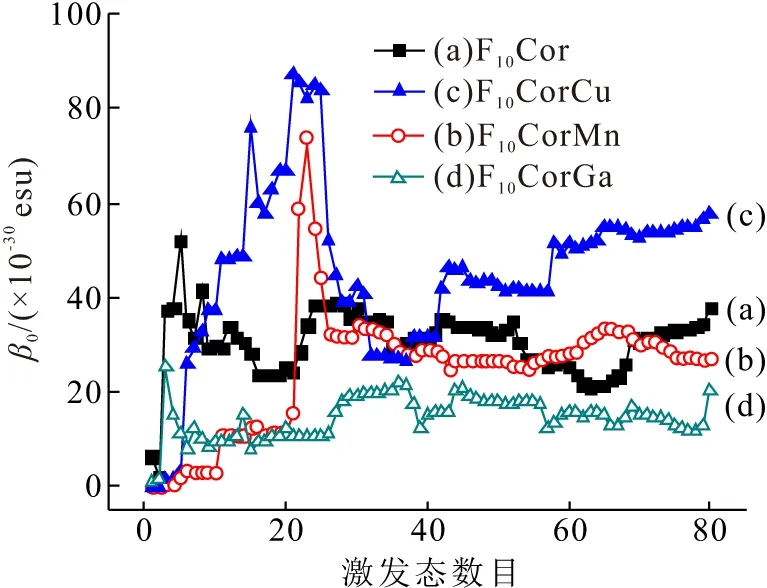
图3 咔咯静态第一超极化率(β0)与激发态数的收敛关系

Figure 3 The convergent behavior of static first hyperpolarizabilities (β0) with the number of excited states for corroles

表5 咔咯静态第一超极化率β0及其分量

注：括号中的数据是动态第一超极化率β1907 nm；β0(CPKS)采用CPKS方法在CAM-B3LYP/aug-cc-pVDZ水平下计算.

根据TD-DFT计算结果，从SOS中简化而来的双能级模型常用于揭示β0与关键激发态的关系：

β0∝fΔμ/ΔE3,

(7)

其中，f为振子强度，Δμ表示基态与激发态之间的偶极矩之差，ΔE为跃迁能. 由双能级模型可知，具有高振子强度、低跃迁能的激发态对β0有显著贡献，此处选取具有最大振子强度的激发态作为关键激发态. 由式(7)可知，β0与f、Δμ成正比，而与ΔE的3次方成反比，可见跃迁能是影响β0大小的重要因素，ΔE越小越有利于表现出更大的β0值. 然而，双能级模型所得计算值(fΔμ/ΔE3) 的变化趋势(表2)与β0的变化趋势(表5)并不完全一致，说明双能级模型无法很好地解释此类咔咯分子的二阶NLO响应差异，这可能是由于双能级模型只假设单一电子激发态对β0有贡献而忽略了其他重要激发态的贡献[10]，另外，振子强度以及基态与激发态的偶极矩之差也是影响β0的重要因素，需要考虑上述因素的共同作用对β0的影响.

为了探索二阶NLO响应的起源，对SOS计算结果进行深入分析，根据β0与激发态数目的收敛关系(图3)，可以考察对β0有重要贡献的主要激发态，其组态系数、分子轨道跃迁性质列于表6. 通过空穴-电子分析[37-38]研究咔咯主要激发态的电子激发特征，其空穴-电子的分布如图4所示. 对F10Cor分子，第3激发态对β0有显著贡献，它具有2个重要组态，分别为0.526 52(HOMO→LUMO+1)和0.410 93 (HOMO-1→LUMO), 由图4A可知，对F10Cor的β0主要贡献是咔咯大环上分子内电荷的转移跃迁. 对F10CorMn，第22、23、24、25和26激发态对β0有明显贡献，它们具有的重要组态分别为0.593 16 (β-HOMO-2→β-LUMO)、0.489 71 (β-HOMO→β-LUMO+5)、0.449 63(β-HOMO-2→β-LUMO)、0.465 16(β-HOMO-2→β-LUMO+1)和0.611 33(β-HOMO-2→β-LUMO+1). 由图4B可知，F10CorMn存在2-氨基苯基到咔咯大环之间的配体内电荷转移(Intraligand Charge Transfer, ILCT)跃迁，并伴随着咔咯大环到金属锰的电荷转移(Ligand-to-Metal Charge Transfer, LMCT)跃迁. 由图4C看出，F10CorMn第23激发态表现出电子激发特征为咔咯大环的ILCT跃迁，并伴随2-氨基苯基到咔咯大环和咔咯大环到金属离子的电荷转移跃迁特征(ILCT和LMCT). 而第24、25和26激发态对β0产生负贡献，主要表现为2-氨基苯基到咔咯大环的ILCT跃迁特征. F10CorMn的2-氨基苯基到咔咯大环的配体内电荷转移(ILCT)跃迁对第一超极化率有显著贡献. 同样地，分析F10CorCu可知，其主要的贡献态为第6、21和26激发态，其主要分子轨道构成成分为0.703 04(β-HOMO-1→β-LUMO)、0.313 36(β-HOMO-3→β-LUMO+1)、0.802 22(β-HOMO→β-LUMO+2). 由图4G可知，F10CorCu第6激发态表现为2-氨基苯基到咔咯大环的ILCT跃迁，由图4H、I可知，第21、26激发态分别表现为2-氨基苯基和咔咯大环的ILCT跃迁. 综上可得，F10CorCu的2-氨基苯基到咔咯大环的ILCT跃迁对β0有重要贡献. F10CorGa与F10Cor存在相似的电子激发特点，第3激发态也对β0有重要贡献，它有2个重要组态分别为0.565 36(HOMO-1→LUMO+1)和0.385 72(HOMO→LUMO)，空穴-电子分布(图4J)表现为咔咯大环上的ILCT跃迁. 总之，β0随激发态数目增加的变化主要来源于各激发态对β0的贡献，例如F10CorCu前40态中存在多个激发态对β0有不同程度的正、负贡献(图3)，这些贡献源于不同电子激发特征的电荷转移(ILCT、MLCT)跃迁, 当激发态产生负贡献时，出现先增大后减小的显著变化现象，而随着激发态数目继续增加对β0的贡献很小，因而β0逐渐呈收敛趋势.

表6 计算所得咔咯主要激发态序号、组态系数、主要贡献和对应分子轨道跃迁

Table 6 The calculated major excited states, configuration coefficients, contribution and corresponding MO transitions of corroles

化合物激发态序号组态系数主要贡献率/%分子轨道跃迁F10Cor30.526 5255HOMO→LUMO+10.410 9334HOMO-1→LUMOF10CorMn220.593 1635β-HOMO-2→β-LUMO230.489 7124β-HOMO→β-LUMO+5240.449 6320β-HOMO-2→β-LUMO250.465 1622β-HOMO-2→β-LUMO+1260.611 3337β-HOMO-2→β-LUMO+1F10CorCu60.703 0449β-HOMO-1→β-LUMO210.313 6610α-HOMO-3→α-LUMO+1260.802 2264β-HOMO→β-LUMO+2F10CorGa30.565 3664HOMO-1→LUMO+10.385 7230HOMO→LUMO

图4 咔咯中对静态第一超极化率(β0)有重要贡献的激发态空穴(蓝色)和电子(绿色)分布

Figure 4 The hole (blue) and electron (green) distribution of major contribution excited states to static first hyperpolarizability (β0) for corroles

利用SOS方法也可计算光辐照作用下的动态第一超极化率βω. 在波长为1 907 nm的光电场作用下，对于F10Cor、F10CorMn、F10CorCu和F10CorGa，其动态第一超极化率β1907 nm相比于β0均有所增大(表5), 说明光的辐照对咔咯分子β0有一定的影响，其原因是光电场作用下咔咯分子表现出共振色散行为[39]. F10Cor在1 907 nm波长的光辐照作用下的β1 907 nm约为β0的1.6倍，F10CorMn、F10CorCu和F10CorGa均表现出相同的变化趋势，β1907 nm约为β0的2倍.

图5表示在输入光子能量0～1.4 eV范围内咔咯化合物动态第一超极化率的色散行为. 当入射光电场大于1.0 eV时，F10Cor及配位化合物表现出不同共振色散行为，其共振峰处于1.0～1.2 eV的能量范围内，其中F10CorMn的共振峰位于1.08 eV(1 140 nm)，相应的动态第一超极化率高达1.50×10-26esu. 而当入射光能量小于1.0 eV时，F10Cor及配位化合物的动态第一超极化率变化趋势十分平稳，因而在1 907 nm(0.65 eV)光辐射下F10Cor及配位化合物未表现出强的色散效应. 图6为1 907 nm下动态第一超极化率βω与激发态数目之间的收敛关系. F10Cor及配合物的动态二阶NLO响应(β1907 nm)顺序为F10CorCu(103.94×10-30esu)、F10Cor(60.60×10-30esu)、F10CorMn(48.75×10-30esu)、F10CorGa(34.39×10-30esu)，这与β0的大小顺序保持一致(图3).

图5 计算所得咔咯动态第一超极化率βw的色散行为

Figure 5 Calculated dispersion behavior of dynamic first hyperpolarizabilityβwfor corroles

图6 咔咯动态第一超极化率(β1 907 nm)与激发态数目之间的收敛关系

Figure 6 The convergent behavior of dynamic first hyperpolarizabilities (β1 907 nm) with the number of excited states for corroles

3 结论

运用密度泛函理论(DFT)计算研究了5,15-二(五氟苯基)-10-(2氨基苯基)咔咯及金属配位化合物(F10CorM, M=Mn,Cu,Ga)的几何结构、电子光谱等，并利用态求和方法(SOS)计算了二阶非线性光学(NLO)系数(β0). 结果表明：这些咔咯化合物的二阶NLO响应主要源于βy的贡献，F10CorCu具有最强的静态二阶NLO响应(β0=57.75×10-30esu)，其二阶NLO响应主要来源于β-HOMO-1→β-LUMO轨道跃迁，表现为2-氨基苯基与咔咯大环之间的配体内电荷转移(ILCT)跃迁. 而与F10Cor(β0=37.92×10-30esu)相比,F10CorMn、F10CorGa的βy分量均明显减小，表现出较弱的二阶NLO响应(β0=27.10×10-30、20.00×10-30esu)，对β0有明显贡献的分别是2-氨基苯基与咔咯大环之间的ILCT跃迁和咔咯大环上ILCT跃迁. 在波长为1 907 nm的光辐照下，F10Cor及配位化合物未表现出强的色散效应，其动态二阶NLO系数约为β0的2倍. 总之，咔咯化合物的二阶NLO响应显著强于卟啉和KDP等非线性光学材料，可为二阶NLO分子的设计提供良好的平台.