自然数方幂和的一种新计算方法

乔盛元，梁亦孔

（上海工程技术大学 a.城市轨道交通学院；b.数理与统计学院，上海 201620）

1 研究背景

自然数方幂和是一个古老的问题，从阿基米德(公元前287—212 年)开始，到雅各布·伯努利(1654—1705 年)在《猜度术》得到任意次幂的求和公式，不少书籍都略有提及[1].很多研究者采用逐差法、伯努利数Bn的性质、递推方法、组合数学中的母函数理论和排列组合知识等得到许多研究结果[2−6].

2 定理证明

2.1 预备定理及证明

引理1根据推广的积分第一中值定理[8]，若函数f(x)与g(x)在闭区间[a,b]上连续，且g(x)在[a,b]上不变号，则在[a,b]上至少存在一点ξ，使得

2.2 用第二类数学归纳法导出关键定理

证明用第二类数学归纳法，只需假设对任意的正整数m，都有

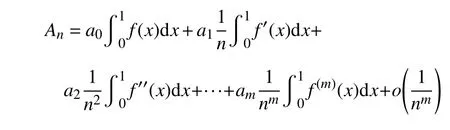
且前m项、前m−1项、前m−2项…前1 项系数分别满足

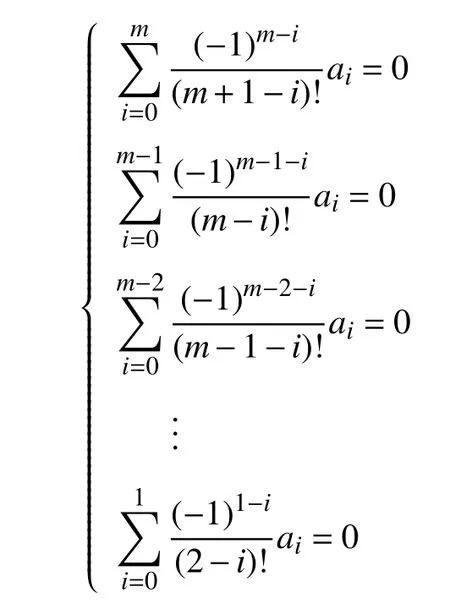
只需证明此规律对m+1项也成立，即可证明An可以展开成

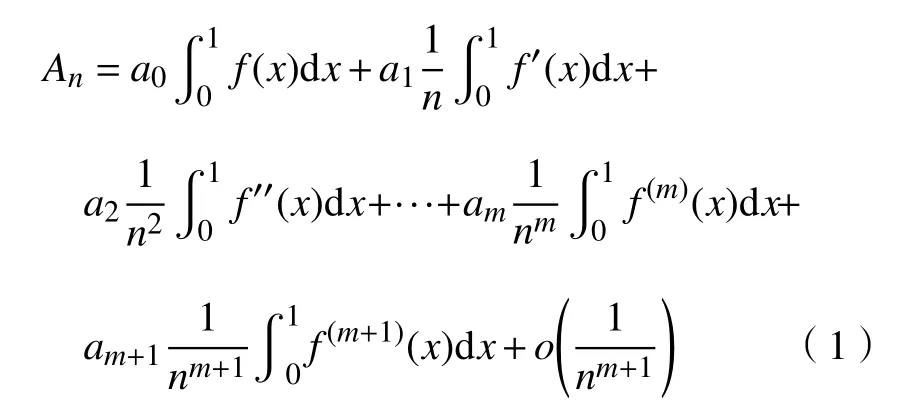
且前m+1项系数也满足

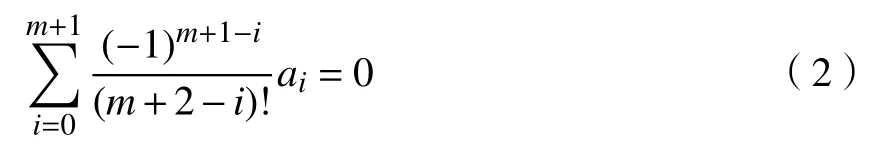
式（1）和式（2）为待证问题.因为m是 任意自然数，故若式（1）和式（2）得证，令m→+∞即可证明该定理.

根据引理2，将函数f(x),f′(x),···,f(m)(x)进行泰勒展开，得

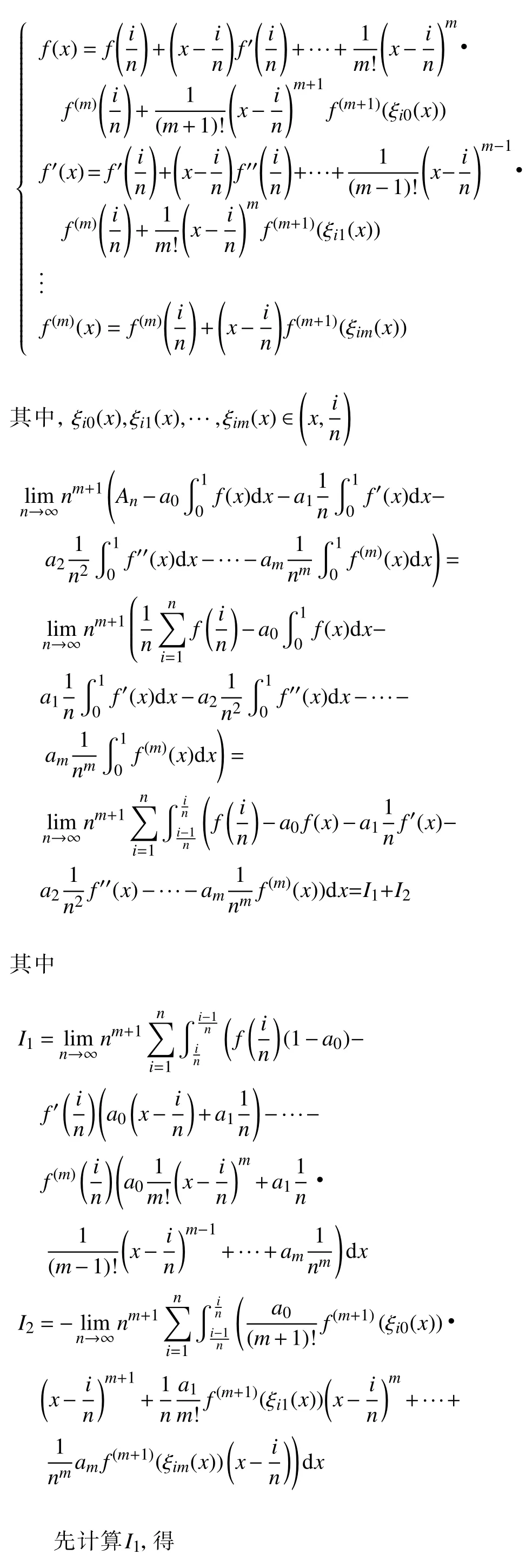
等式最右侧有极限值存在，因此

因此式（2）已被证明，所以定理得证.

3 应用举例

当m取 自然数时，用定理求解过程如下.

4 结语