非对称围壁加强对耐压圆柱壳孔口应力影响分析

张帆晨，和卫平，马建军

(武汉第二船舶设计研究所，湖北 武汉 430061)

0 引 言

水下航行器必须有坚固的耐压船体来承受巨大水压力。但由于实际需求，往往要在水下航行器的耐压结构上开各种各样的孔，这些孔的存在破坏了耐压圆柱壳的结构连续性，改变了开孔区域的应力分布，产生开孔处应力集中现象，严重降低耐压圆柱壳的极限承载能力。工程上会采取各种补强措施来弥补由于开孔导致的被削弱壳体强度，避免在开孔周围造成的应力集中问题。圆柱壳开孔问题，国内外学者做了大量的研究。SangEuilee 等[1]用有限元方法探究了在开孔后的壳体的极限强度问题。Talezadehlari 等[2]研究了复合材料圆柱壳开孔加强的问题。朱邦俊和王玉华[3]对带有开孔的薄壁圆柱壳进行了有限元分析，得到了开圆孔的薄壁圆柱壳的应力特性。许兵[4]对切断一根肋骨的用围壁加强的正交单圆孔进行了分析。施涛[5]研究了典型耐压船体开孔加强结构并进行了优化分析。周猛猛[6]对围壁加强的圆柱壳开孔结构进行了有限元分析。舒斌[7]用Ansys 软件建立了大开孔圆柱壳采用围壁补强的模型，用2 倍斜率法确定其极限载荷值。Obodan 等[8]研究了薄壁圆柱壳非线行与稳定性。Aninash R. Kharat 等[9]研究了不同形式的加强构件对于加强件以及孔边应力的影响，针对4 种加强构件的设计方式详细分析了不同的加强构件对应力产生的影响。张锦岚[10]采用参数化建模方式，讨论了多参数对于开孔周围应力的影响。

对于单壳体的水下航行器，开孔只能采用“单边围壁”加强方式，即孔口围栏外伸段极短（或缺失），确保围栏不突出于壳体外，这种极端非对称围壁加强结构不仅改变了传统开孔区应力特性，并使空口应力场复杂化，而且大大削弱了加强效果，严重影响开孔强度。

目前针对单边加强技术研究较少，基础比较薄弱，因此研究非对称开孔加强具有重要意义。本文针对典型的圆柱壳结构，通过数值分析的方法，探究圆柱壳开孔非对称加强的变化规律，为以后设计提供参考。

1 数学模型

1.1 几何模型

圆柱壳模型如图1 所示。2 种颜色代表2 种不同刚度材料（材料参数见表1）。两端部设置过渡段以及封板（这部分的设置主要是模拟试验过程中的边界条件，封板用于密封，过渡段用于消除封板对壳体边界应力的影响，其刚度大于壳体刚度）。

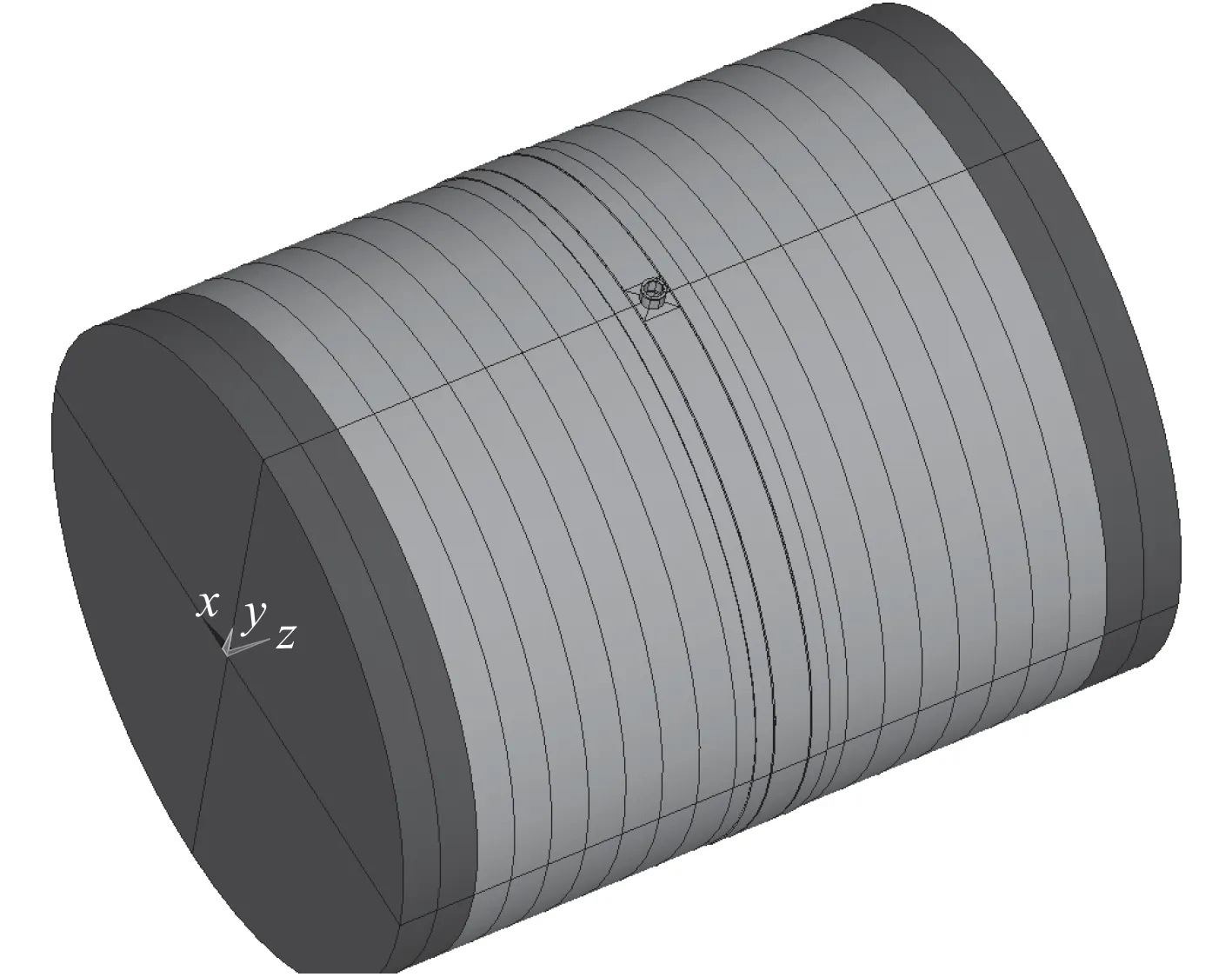
图 1 圆柱壳几何模型Fig. 1 Geometric model of cylindrical shell

表 1 圆柱壳材料参数Tab. 1 Parameters of material

圆柱壳模型相关尺寸进行了无因次化处理，具体如表2 所示。

表 2 圆柱壳几何参数Tab. 2 the parameters of the cylindrical shell

1.2 有限元方法

计算模型网格采用体-壳结合的形式，在开孔附近区域采用体网格，在其余部分采用壳网格。体网格与壳网格之间采用MPC 单元连接。这样做既能够提高计算的准确性，又不至于导致大量的计算。MPC 单元提供了一个极为有效的接触模拟算法，能够很好实现壳体和实体的绑定约束。

边界条件为：Z=0（U X=0，U Y=O，U Z=0，RTOX=0，RTOY=0，RTOZ=0）：z=L（UX=0，UY=O，RTOX=0，RTOY=0，RTOZ=0。耐压体上加载的压力为6.75 MPa，加载及边界条件示意图如图2 所示。

图 2 圆柱壳边界条件以及加载情况Fig. 2 Boundary condition and the pressure of the cylindrical shell

有限元网格总量为218 685（包括MPC 单元），其中体网格、壳网格以及MPC 单元的数量分别为17 627，34 886，7 520。

图 3 圆柱壳网格示意图Fig. 3 Mesh of the cylindrical shell

图 4 加强围壁网格示意图Fig. 4 The mesh of the enclosing wall

2 数值模拟结果分析

2.1 对称围壁高度变化对孔口应力的影响

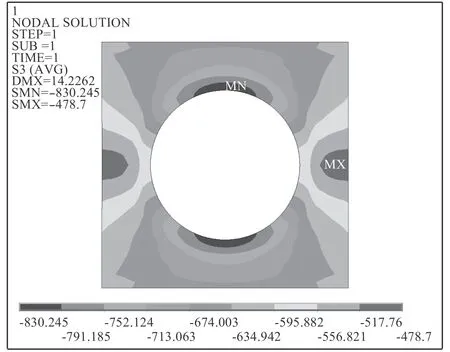
图 5 孔边壳板应力分布Fig. 5 Stress distribution of the shell around opening

图 6 围壁应力分布Fig. 6 Stress distribution of the enclosing wall

开孔周围壳板的应力分布如图5 和图6 所示。应力的最大值发生在围壁与壳板的相贯线处。图7 和图8 的计算结果表明。对于开孔的对称围壁加强，不同的开孔半径，应力水平不同，半径越大，孔边的应力水平越高：R200＞R160＞R135。随着围壁高度的增加，孔边应力不断地减小，减小的趋势先快后慢，最后趋于某一个值，这个值通常称为围壁的“有效高度”。一般来说，有效高度是指在这个高度范围内，围壁的增长能有效减少孔边应力集中的现象，一旦超过此高度范围，围壁的增长不再有效。

图 7 孔边壳板应力载荷比随围壁高度变化示意图Fig. 7 Stress on the shell around the opening

当压力作用在耐压圆柱壳上的时候（见图9），围壁将会在压力的作用下发生变形，图中A 点处的应力将会因此而增加，因此最大应力值发生在围壁与壳板的相贯线处，围壁的变形随远离相贯线处而减小，因此应力水平也逐渐减小。

图 8 围壁应力载荷比随围壁高度变化示意图Fig. 8 Stress on the enclosing wall

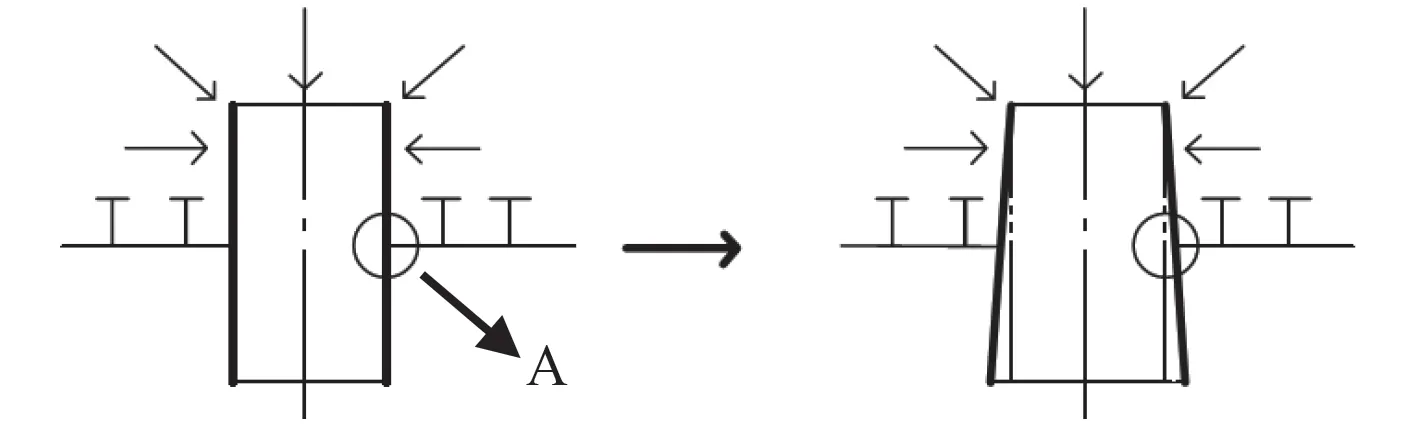
图 9 围壁在载荷下的变化示意图Fig. 9 Variation of the enclosing wall under the pressure load

2.2 非对称围壁高度变化对孔口应力的影响

对于单壳体水下航行器来说，相比双壳体，其几何形状受到限制，为了保证航行器外形线光顺，只能采用单壳体加强的方式来进行开孔补强。单边加强的孔口应力状况将更加复杂，规律是否与对称加强一致，是需要进行探究的问题。

图10～图12 分别为在固定围壁外长为50 mm，100 mm，125 mm 的情况下，只改变围壁内长的Ansys有限元计算结果，图中的取值为壳板开孔处同一点的应力值。对于不同的固定围壁外长以及不同的开孔半径而言，开孔边缘的壳板应力随着围壁内长的变化呈现出相似的趋势。随着围壁内长的增加，应力集中逐渐减小，最后趋于一个稳定值。这说明围壁内长达到了“有效高度”，这与之前对称围壁补强的趋势类似。

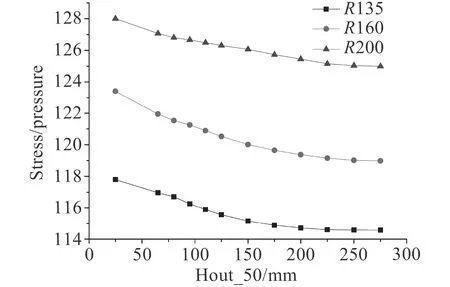
图 10 外伸围壁高度为50 mm 时随着围壁内高增加孔边壳板应力变化示意图Fig. 10 Height of the enclosing wall above the shell is 50 mm

图 11 外伸围壁高度为100 mm 时随着围壁内高增加孔边壳板应力变化示意图Fig. 11 Height of the enclosing wall above the shell is 100 mm

图 12 外伸围壁高度为125 mm 时随着围壁内高增加孔边壳板应力变化示意图Fig. 12 Height of the enclosing wall above the shell is 125 mm

图 13 外伸围壁高度为50 mm 时随着围壁内高增加围壁应力变化示意图Fig. 13 Stress on the enclosing wall

图13 为与壳板边缘对应的围壁上的同一处的应力取值。该曲线为开孔半径为200 mm 围壁外长固定50 mm时的应力值变化趋势图，作为对比参照可见，同一点处不论是围壁还是壳板上的应力都是随着内长的增加而减小最后趋于稳定。

当围壁内长固定，只改变外长的情况下，开孔边缘壳板的应力变化（见图14）以及围壁上同一点应力的变化趋势（见图15）仍然表现为：随着围壁外长的增加，应力集中减小，最后应力值趋于某一个稳定的数值，说明此时围壁达到了其“有效高度”。实际上，固定围壁内长不断增加围壁外长的情况，在工程中并不会常遇到，因此该规律仅作参考。

2.3 非对称围壁厚度变化对孔口应力的影响

图 14 围壁内伸高度为50 mm 时随外伸高度变化孔边壳板应力变化示意图Fig. 14 Height of the enclosing wall inside the shell is 50 mm

图 15 围壁内伸高度为50 mm 时随外伸高度变化围壁应力变化示意图Fig. 15 Stress on the enclosing wall

前文中提到，围壁的高度是不能够无限延长的，它最终会达到一个“有效高度”，在此高度范围之外，无论高度再怎么变化，对于应力的改善不再有明显的效果。因此，对于非对称围壁，保持其他变量一定，探究增加围壁厚度对孔口应力的影响。图16 为计算时孔边壳板的应力分布，计算结果如图17 和图18所示。随着围壁厚度的增加，孔边壳板处的应力值减小，最后趋于稳定值。这说明围壁的厚度存在一个类似“有效高度”的“有效厚度”，在“有效厚度”的范围内，增加厚度能有效改善孔边应力集中现象，当厚度超过这一值，增加厚度将不再有明显的效果。围壁的应力值变化如图19 所示。随着厚度的增加，围壁应力变化不断减小并趋于平缓，说明围壁厚度的增加对于壳板以及围壁的应力改善都有较为明显的效果。

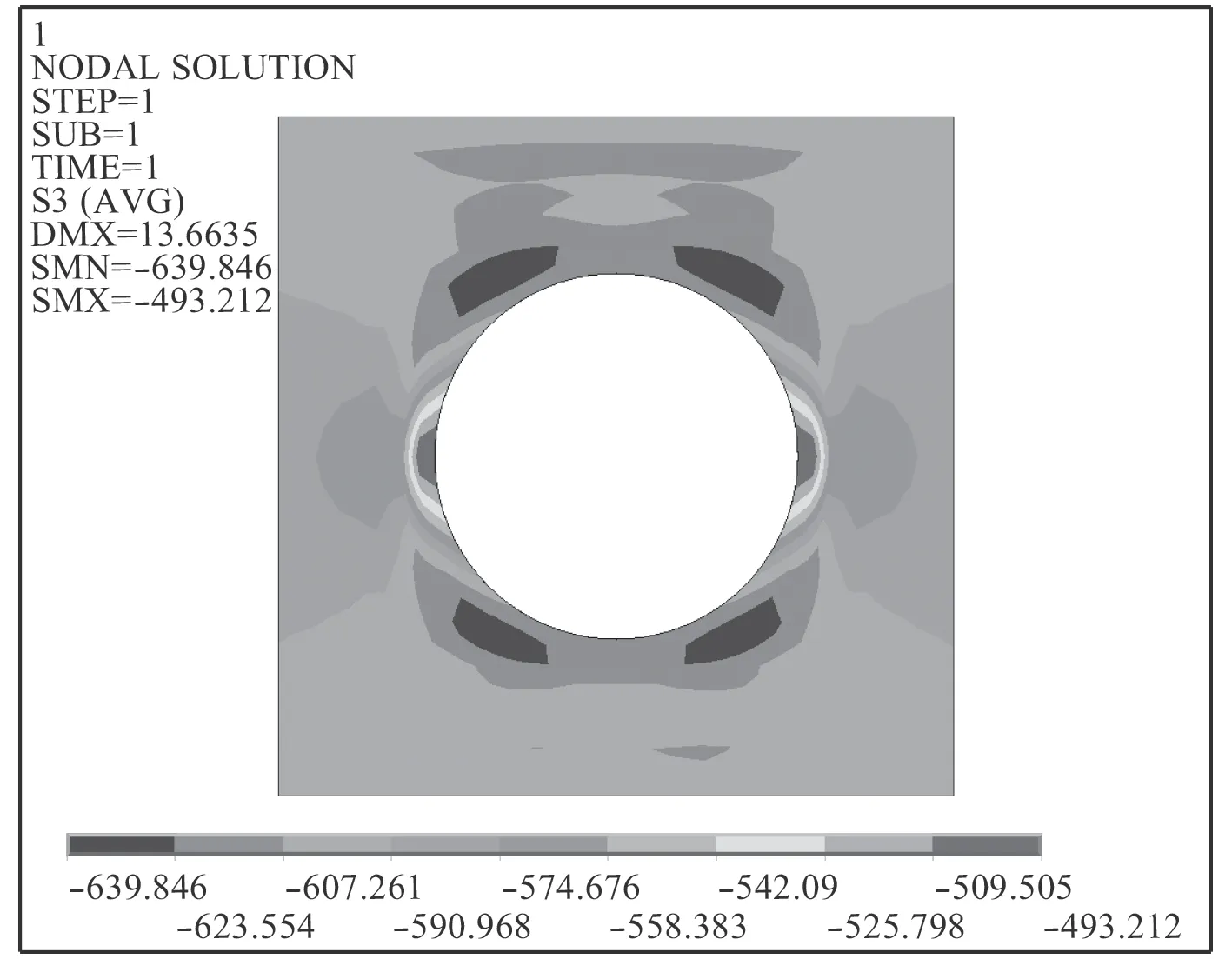
图 16 开孔周围壳板应力分布（围壁厚度=40 mm）Fig. 16 Stress distribution of the shell around opening（thickness=40 mm）

图 17 应力载荷比随着围壁厚度增加变化示意图（不同曲线代表不同半径）Fig. 17 Stress varies with different thickness

图 18 应力载荷比随着围壁厚度增加变化示意图（不同曲线代表外伸高度为50 mm 时不同内伸高度下厚度变化趋势）Fig. 18 Stress varies with different thickness（different height inside the shell）

图 19 厚度变化时围壁应力变化趋势示意图Fig. 19 Stress on the enclosing wall for different thickness

3 有限元数值解

通过对单壳体非对称围壁补强的研究，得出以下几点结论：

1）基于数值分析的结果，不论是对于对称的围壁补强，还是非对称的围壁补强，随着高度或者厚度的增加，孔边壳板的应力值都会减小最后趋于一个稳定值，这个值称为“有效高度”或者“有效厚度”。因此在进行围壁补强设计时，应首先找到有效高度值，在有效高度范围内再根据具体要求进行调整设计。

2）对于单壳体水下航行器，其受几何形状限制，只能采用单边加强的方式进行补强，孔口的应力场将更加复杂，其加强规律是非常值得探究的。本文计算结果表明，对于非对称围壁的开孔补强，不论是开孔边缘的壳板上的应力还是围壁上的应力，随着围壁高度（厚度）的增加，其值都会减小最后趋于稳定。但是对于非对称而言，“有效高度’的值通常会比对称的围壁补强的大一些。原因在于单边加强相比较对称加强，由于围壁外伸出壳体的长度受到限制，高度通常较小，大大减弱了加强效果，因此需要更长内伸的围壁来弥补缺失的效果。

3）当围壁的高度达到了“有效高度“之后，增加围壁的厚度往往能够继续减小孔边的应力集中。因此在进行非对称围壁补强件设计时，综合考虑高度与厚度的值，进行优化能够最大限度的达到理想的效果。

本文重点研究单壳体水下航行器的开孔非对称围壁补强，进行一系列的数值仿真分析。结果表明，非对称与对称的围壁补强在减小孔边应力集中的问题上，应力随着围壁变化而变化的趋势大致相似，但是具体数值有一定的区别。今后，将探究采用非对称围壁开孔加强结构圆柱壳的稳定性问题；切断肋骨情况下，采用非对称围壁加强的圆柱壳强度、稳定性等问题。