与圆有关的计算复习设想

王秀娟

一、中考考点透视

本节包括正多边形与圆的计算、弧长、扇形面积以及圆锥、圆柱的侧面积的计算等内容。利用上述公式解决问题是本节的重点内容。

二、应考策略

随着新课程标准对圆的证明要求的降低，圆的有关计算逐步成为近年中考的热点问题。中考中此类问题既有低档的填空题、选择题，又有中档的解答题，分值在6分左右。复习中我们首先要记准正多边形与圆的有关概念、弧长公式、扇形的面积公式以及圆锥的侧面面积的计算方法，其次就是加强对这些公式在生活实际中的应用性问题的训练，最后还要注重数形结合以及转化的数学思想，培养学生的空间观念，使学生对圆的认知更全面完整。

三、复习模式

基本模式为“23335”阳光高效课堂模式，即“双向、三段、三学、三导、五步”。“双向”指整个学习过程中教师和学生的双边活动;“三段”指教师和学生学习的三个时段，即课前、课中、课后;“三学”即独学、对学、群学;“三导”模块即预习、展示、反馈;“五步”指课堂导学的五个步骤，即自主预习、合作探究、展示交流、达标检测、反思评价。

四、复习题的设置

（一）热身训练

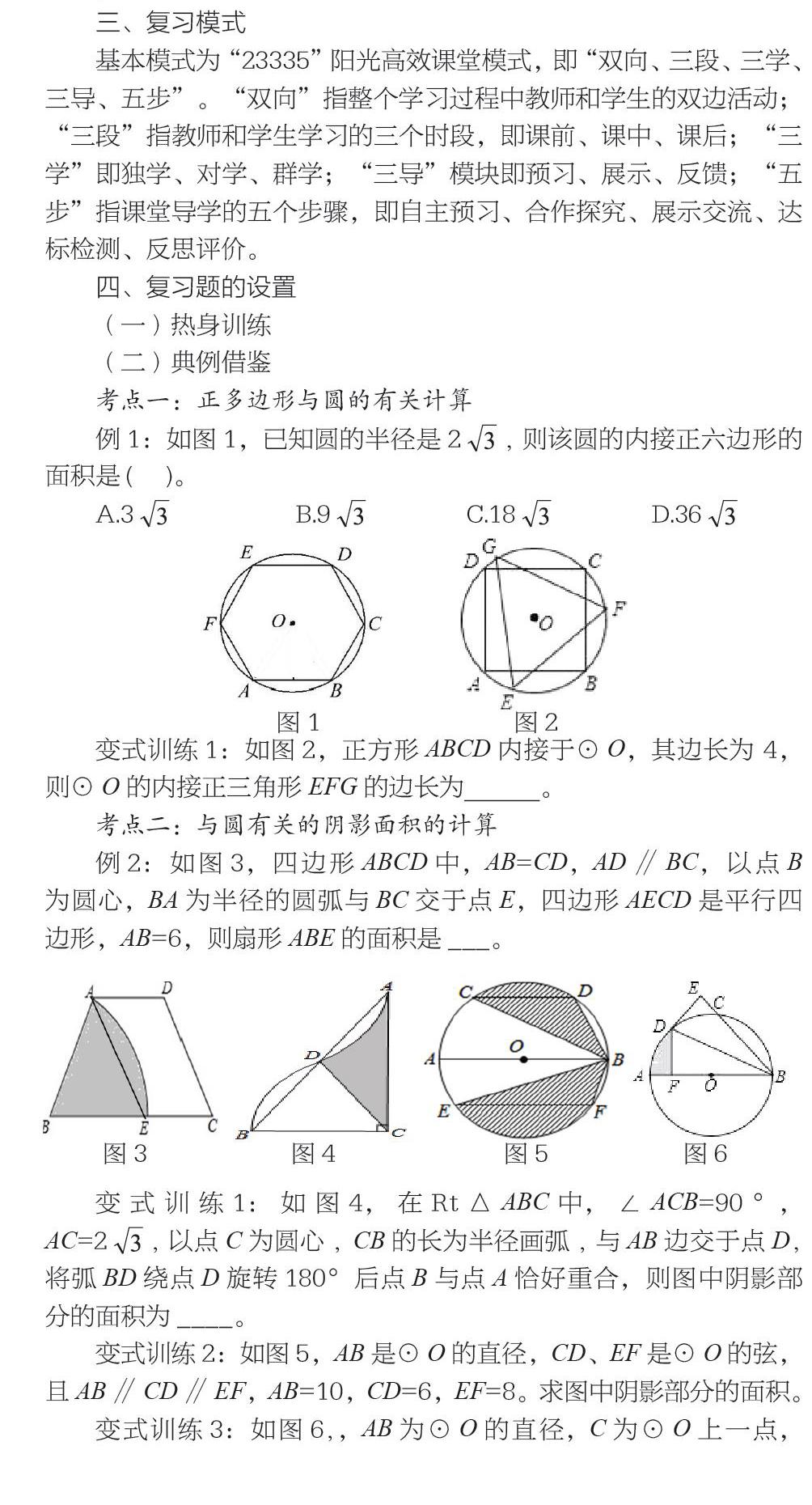
（二）典例借鉴

五、设想的原因和目的

（一）课前

让学生复习课本和同步上与圆有关的计算相关内容。因为新授时我是以它们为主要材料学习的，所以课前让学生独立看课本和同步学习，这样可以让学生在较短的时间里复习相关内容。

（二）課中

1.复习导入

首先通过一组比较简单的练习题带出知识点，让学生自己独立完成。如果单纯提问与圆有关的计算定义、公式，那么就显得有些枯燥低效，所以我是通过设置四个简单的习题，使学生见题想定义、公式等，接着让同桌两人把刚才的知识根据图形相互总结和补充，最后让学生上台进行展示板书反馈。

如果设圆锥的母线长为R，底面圆的半径为r，侧面展开图的弧长为l，圆心角为n°，那么可以得到：（1）l=;（2）S扇形=;（3）S侧面积=πRr;（4）l=2π r;（5）nR=360°r;（6）正n边形的中心角=。

2.正多边形与圆的有关计算

例1 比较简单，主要让学生自己完成并进行反思：（1）正n边形的中心角等于;（2）求正多边形的面积，常常转化为求三角形的面积;（3）有关正多边形的计算常常转化成解直角三角形;（4）数学思想：转化的数学思想。

我选择变式的原因：一是和例1类似，二是让学生再次复习含120°的等腰三角形三边的比是1∶1∶。

3.与圆有关的阴影面积的计算

与圆有关的阴影面积的计算是各地中考试题命题的热点，常与三角形、四边形、旋转、切线等结合进行命题，试题难易度变化较大，呈现形式多样化，有选择题、填空题和解答题。

例2 和变式相对来说有点难度，所以让小组群学并进行展示，组际之间也可互帮互助，最后师生共同总结阴影面积的求法：公式法、和差法、等积变形法。直接求面积较麻烦或根本求不出来时，常通过平移、旋转、割补、等积变形等，为公式法或和差法创造条件。

4.圆锥的有关计算

（1）在解决圆锥侧面展开图的问题时，常借助平面展开图的弧长等于圆锥的底面周长，即=2πr，得出nR=360°r，利用这个公式求n，R，r都比较方便。

（2）常把圆锥的侧面展开图转化为平面解决最短路径问题。

（三）课后

自己搜集与本节内容相符甚至变式的拓展性练习题，并且与同学分享较中意的习题;独立完成说明指导本节内容。

最后，我借鉴叶圣陶老先生的话和大家共勉：“教师之为教，不在全盘授予，而在相机;必令学生运其才智，勤其学习，领悟之源广开，记熟之功弥深，乃为善教者也。”

【备注：本文系山东省教育教学研究课题：一般课题 《农村初中构建“23335”阳光高效课堂教学模式研究》的研究成果，课题立项编号：2018JXY1081】