基于Ruger 近似式预测裂缝型储层的可行性研究

吴姗姗，高 刚，桂志先，王 鹏，李成毅

(1.长江大学油气资源与勘探技术教育部重点实验室，湖北 武汉 430100；2.长江大学地球物理与石油资源学院，湖北 武汉 430100；3.中国石油集团川庆钻探工程有限公司地球物理勘探公司，四川 成都 610213)

裂缝型储层的预测方法根据资料来源通常分为两类：一类是通过测井资料与岩心露头资料定量识别储层的裂缝，该方法预测结果精度较高，但其结果难以外推至井间[1]；另一类是通过地震资料定性预测储层的裂缝，由于地震资料有横向分辨率高、勘探成本较低、数据分布范围广等特点，因而运用地震资料检测裂缝的方法广泛应用于裂缝型储层的预测[2]。目前运用地震资料检测裂缝的方法主要有：①叠后地震属性分析法，即利用叠后资料分析其地震属性，如相干属性[3]、曲率属性[4]、蚂蚁体属性[5]等；② 转换波裂缝检测法，利用横波分裂产生的快慢横波时差来反映裂缝发育的主方向和裂缝密度，常用的方法有相对时差梯度法[6]和层剥离法[7]；③叠前纵波方位各向异性检测法，利用纵波各向异性进行裂缝检测的方法有动校正(Normal Moveout Correction，简称NMO)速度方位变化裂缝检测法、正交地震测线纵波时差裂缝检测法、纵波方位AVO(Amplitude Variation with Offset and Azimuth，简称AVOZ/AVAZ)和纵波阻抗随方位角变化(Impedance Variation with Azimuth，简称IPVA)裂缝检测法[8]。

利用叠前纵波资料的方位各向异性特征来识别裂缝型储层是目前应用最为广泛的方法之一。该技术的研究始于20 世纪70 年代，由于受到当时勘探条件的限制，直到20 世纪90 年代，I.Tsvankin[9]和A.Ruger[10]分别推导了HTI(Horizontal Transverse Isotropy，简称HTI)介质中纯模式波的动校正速度随方位角变化(Velocity Variation with Azimuth，简称VVA)和纵波的反射系数随入射角和方位角变化(AVOZ/AVAZ)的近似公式之后，该技术才引起了广泛的关注。随后S.Malick 等[11]、范国章等[12]、朱成宏等[13]、朱兆林等[14]对地震波方位AVO 特性进行了全面的分析，建立了地震波方位AVO 的变化特征与裂缝走向、倾向以及发育强度的关系，该方法在实际裂缝检测应用中也取得了很好的效果[15-19]。该方法在具体应用时仅考虑了各向异性参数对地震响应特征的影响，并未考虑岩性参数对地震响应特征的影响。然而，在实际资料的应用过程中发现，在储层与盖层的弹性参数存在较为严重叠置现象的情况下，常规的弹性参数预测储层难度较大，虽然裂缝参数预测纵波方位各向异性的相关技术方法可以提高储层的预测精度，但是存在一定的多解性。因此，笔者以Ruger 近似式为基础建立模型，将模型中各向异性参数和岩性参数设置为概率密度分布函数，通过Monte Carlo 随机方法进行叠前AVAZ正演模拟拟合椭圆，进而分析各参数的随机分布对拟合的椭圆信息即裂缝信息的影响。

1 叠前AVAZ 技术检测裂缝原理

1.1 常用裂缝模型

在众多的裂缝岩石物理模型中，目前最为常用的模型是Hudson 的薄硬币模型和Schoenberg 的线性滑动模型。

Hudson 模型主要是描述弹性固体中包含薄硬币形状的椭球裂缝的等效介质模型，该模型主要通过裂缝密度e和裂缝的纵横比χ来表征裂缝系统，裂缝的密度是采用裂缝体积密度的定义方式：

式中a是裂缝的半径；N/V是单位体积内裂缝的数量；φ是裂缝诱导的孔隙率；χ是裂缝的纵横比。

Schoenberg 线性滑动模型是基于Backus 细层层状介质模型提出的。该模型在岩石物理模型的研究中，适用于具有线性连续边界的、充满弱强度(充填物弹性模量小)介质的平行层模型。C.J.Hsu 等[20]提出了两个无量纲的参数，用来描述由裂缝引起的岩石刚度变化特征。

式中ΔN和ΔT分别代表由裂缝引起的垂直于裂缝面方向和平行于裂缝面方向的弹性参数差值，它们的变化范围为0～1；EN和ET为非负的、无量纲的与裂缝有关的柔度参数；ZN为垂向柔度；ZT为平行于裂缝面的柔度；μ、λ为拉梅参数。

两种模型参数之间具有一定的关联性，ΔN和ΔT与裂缝参数之间的关系见式(4)和式(5)。

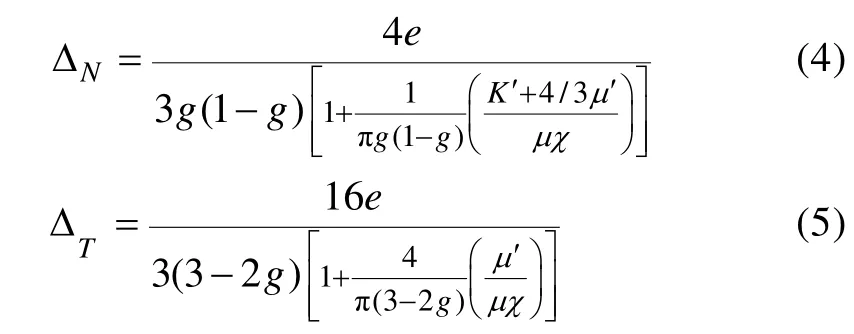
式中g=μ/(λ+2μ)；K′和μ′是缝隙中充填物的体积模量和剪切模量。

A.Bakulin 等[21]给出了HTI 介质中各向异性参数(ε(V)、γ、δ(V))与Schoenberg 裂缝模型岩石物理参数(ΔN和ΔT)之间的关系，如式(6)—式(8)所示：

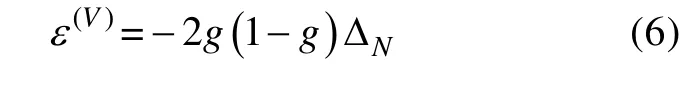
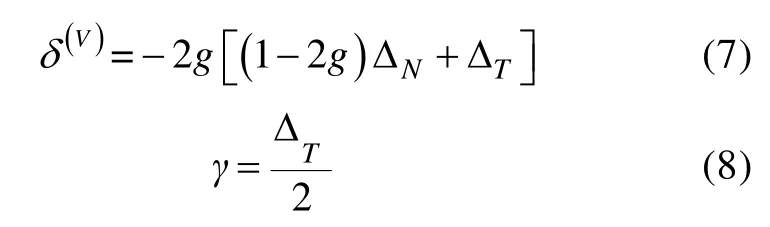
将式(4)—式(5)代入式(6)—式(8)可以得到HTI介质中各向异性参数(ε(V)、γ、δ(V))与Hudson 模型所定义的裂缝密度之间的关系，如式(9)—式(11)所示，揭示了HTI 介质中各向异性参数(ε(V)、γ、δ(V))与裂缝的密度之间的关系，可以分析L.Thomsen[22]各向异性参数与裂缝密度及裂缝中流体之间的关系。

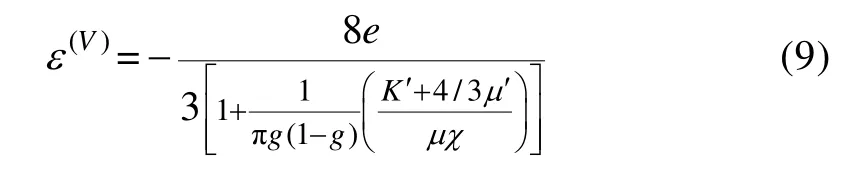
1.2 HTI 介质中叠前AVAZ 技术检测裂缝原理

A.Ruger 等[10]对HTI 介质中地震波传播理论(图1)进行了深入研究后，在弱各向异性的假设条件下，

给出了HTI 介质中纵波的反射系数随入射角和方位角变化的近似公式，即：

式中Z为纵波波阻抗；β为纵波波速；α为横波波速；(ε(V)、δ(V)为不同于L.Thomsen 裂隙参数，后续为了方便，参数直接写为ε、δ)，ε、γ分别表示纵波和横波各向异性；δ表示纵向和横向各向异性；G=ρβ2表示切向模量；i和φ分别为入射方向和测线方向与裂缝对称轴的夹角；符号“-”和“Δ”分别表示上下界面参数的算术平均值、差值。

HTI 介质的各向异性参数的表达式：

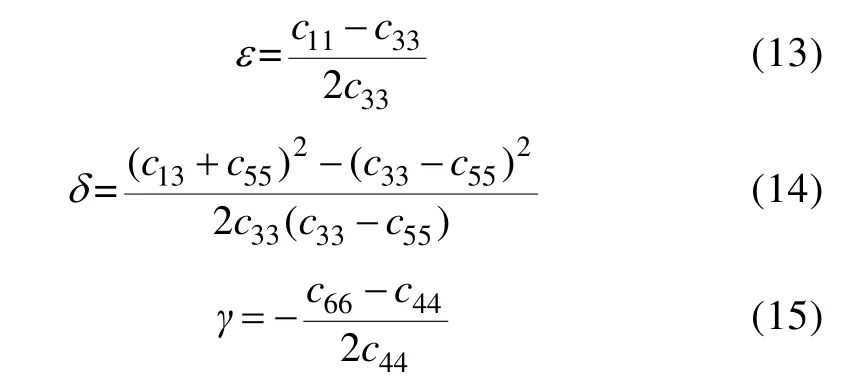
式中cij为HTI 介质弹性常数。

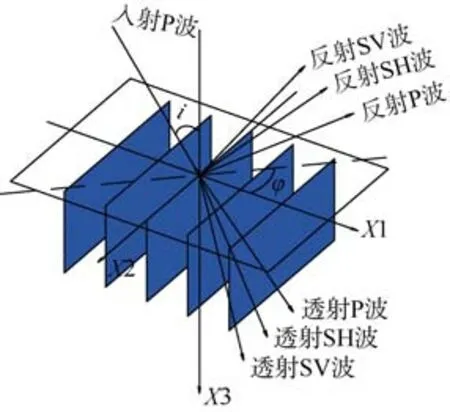
图1 HTI 介质中纵波传播示意图Fig.1 Sketch map of P wave propagation in HIT medium

入射角较小时，各向异性介质中纵波反射振幅与裂缝参数之间的关系可以近似表示为：

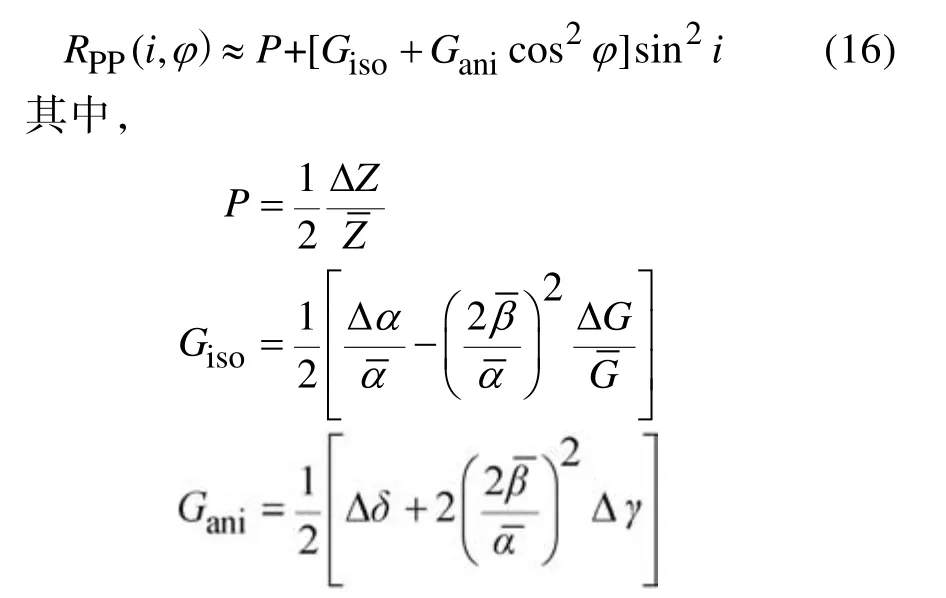
式中P为纵波垂直入射时的反射振幅；Giso为反射振幅随偏移距的变化率，即各向同性梯度；Gani为振幅随偏移距和方位角的变化率，即各向异性梯度，指示了介质受各向异性影响的部分。

在固定入射角的情况下，式(16)可以进一步简化为：

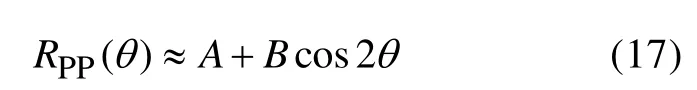
式中A为与炮检距有关的偏置因子；B为与炮检距和裂缝特征有关的调制因子；θ是炮检距方向与裂缝走向的夹角。

式(17)反射系数R随着角度θ的变化可用椭圆状的图形来表示(图2)。

参数A与炮检距有关，反映了岩性变化所引起的振幅的变化量；参数B相当于振幅随炮检距方位改变的变化量，反映了地层裂缝对反射振幅强度的影响，其大小决定了储层裂缝的发育程度，可视为各向异性因子。因此，可以把B/A即椭圆的扁率作为裂缝密度的相对量度，B/A的值越大，说明裂缝发育越好，反之，裂缝发育越差，而对于各向同性介质，A值就是均匀介质下的反射振幅，B值为零。

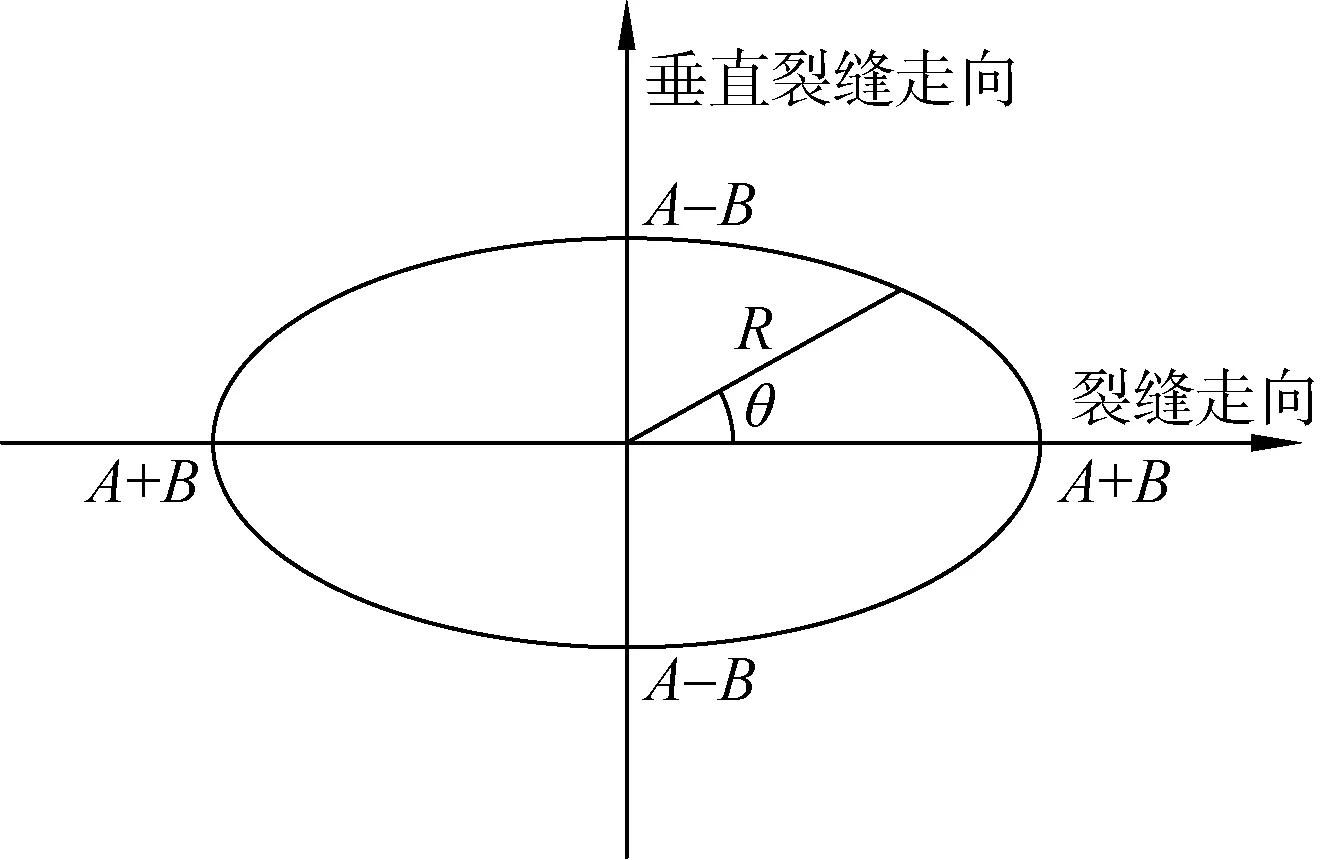
图2 地震反射振幅随方位角变化Fig.2 Variation of seismic reflection amplitude with azimuth

2 Monte Carlo 随机正演模拟

叠前AVAZ 技术检测裂缝法主要是通过地震资料进行椭圆拟合，然后根据椭圆的信息对裂缝进行预测和评价。在实际应用中，当横向岩性变化时，通常是利用平均振幅A的信息，没有考虑横向岩性变化对拟合椭圆信息的影响，这在一定程度上造成了多解性。为了了解横向岩性参数的变化对椭圆拟合信息的影响，对储层物性较好，以孔-缝型、裂缝型储层为主的研究区域的测井资料进行统计，灰岩储层的纵波速度为3 000～5 200 m/s，密度为2.40～2.75 g/cm3，盖层泥岩纵波速度为2 600～4 500 m/s，密度为2.1～2.5 g/cm3，据此建立含EDA 介质的双层模型(图3)。模型参数设置见表1，入射角为30°，采用Monte Carlo 随机方法产生满足条件的随机模型，利用最小二乘法进行椭圆拟合，然后分析Ruger公式(式(12))中各个参数变化对拟合椭圆信息的影响，进而说明该参数对裂缝评价的影响。

图3 含EDA 介质的双层介质模型Fig.3 Two-layer model with EDA medium

2.1 各向异性参数对叠前AVAZ 地震响应影响

首先，通过模型分析各向异性参数单独变化对叠前AVAZ 地震响应特征的影响。L.Thomsen[23]通过实验测定了一系列不同岩性的样品，根据其测定的不同岩性的各向异性参数值进行统计，发现各向异性参数值基本都小于0.2，所以本文模型各向异性参数分别设置为均值0.05、0.10、0.20 的正态分布，其中标准差设置为均值的10%，为了保证拟合出的椭圆扁率变化是由各向异性参数变化所引起，将模型速度和密度设置为固定的平均值(表1)，利用Ruger 近似式进行随机正演模拟，分别作出不同各向异性参数值所对应的椭圆扁率B/A与各向异性因子B散点图(图4)。

表1 双层介质模型参数Table 1 Parameters of a two-layer medium model

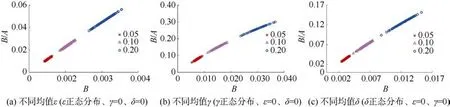
图4 不同各向异性参数的B/A(椭圆扁率)与B(各向异性因子)散点图Fig.4 The scatter plots of B/A and B with different anisotropic parameters

图4a—图4c 分别对应各向异性参数ε(图4a)、γ(图4b)、δ(图4c)为不同均值的正态分布时的椭圆的扁率B/A与各向异性因子B散点图，其中红色、紫色及蓝色分别为模型的各向异性参数值设置为均值0.05、0.10 和0.20 的正态分布结果。由图4 可以看出椭圆的扁率B/A与各向异性因子B的值随各向异性参数值增大而增大，说明各向异性越强，其各向异性因子B与椭圆的扁率B/A值越大，证明了利用纵波方位的各向异性特征检测裂缝是可行的。对比图4a—图4c 可以看到，各向异性参数在同一均值的条件下，参数γ(图4b)对应的椭圆扁率B/A与各向异性因子B的值最大，其次是参数δ(图4c)，参数ε(图4a)最小，因此，各向异性参数γ对椭圆扁率B/A与各向异性因子B影响最大、δ次之、ε最小。

2.2 非各向异性参数对叠前AVAZ 地震响应影响

为了进一步分析非各向异性参数对叠前AVAZ地震响应特征的影响，以各向异性参数γ正态分布为例(各向异性参数γ对叠前AVAZ 响应特征影响最大，模型参数γ设置为均值0.1、标准差0.01 的正态分布)，然后分别将模型中所研究的岩性参数根据表2 设置为正态分布，标准差按照模型4 取值，最后通过Monte Carlo 随机正演模拟得到对应椭圆扁率B/A与各向异性因子B散点图(图5)。

图5a 和图5d 分别是上层和下层的密度设置为正态分布(表2 中模型4)，纵波和横波速度设置为均值时所对应的椭圆扁率B/A与各向异性因子B散点图，可以看出在密度标准差接近均值5%的情况下，其椭圆扁率B/A与各向异性因子B散点图形态与图4b 中γ为均值0.1 模型较为接近，说明密度参数不是影响椭圆信息的主控因素。图5b 和图5e 分别为上层介质和下层介质的横波速度设置为正态分布(表2 中模型4)，纵波速度和密度设置为均值时所对应的椭圆扁率B/A与各向异性因子B散点图，当横波速度的标准差接近均值的10%时，其图形的散点离散程度较密度正态分布时大，与图4b 中γ为均值0.1 的模型结果差异较大，可以看出横波速度随机变化对AVAZ 响应特征的影响较大。图5c 和图5f 分别为上层介质和下层介质的纵波速度设置为正态分布(表2 中模型4)，横波速度和密度设置为均值时所对应的椭圆扁率B/A与各向异性因子B散点图，综合来看，当纵波速度所取的标准差接近均值的10%时，其图形的散点扩散程度最大，与图4b 中γ为均值0.1 的模型结果差异很大，说明纵波速度的随机变化对AVAZ 响应特征的影响最大。

表2 不同标准差的岩性参数表Table 2 Lithology parameters with different standard deviations

图5 不同非各向异性参数B/A(椭圆扁率)与B(各向异性因子)散点图(γ 随机变化、ε=0、δ=0)Fig.5 The scatter plots of B/A and B with different non-anisotropic parameters(γ random variation,ε=0,δ=0))

对式(12)进行理论分析，可以看出公式中的密度参数对椭圆的拟合影响较小，速度参数影响较大。式(12)的理论分析结果与上述模型分析结果相符合，因此，模型速度与密度的不确定性会对模型模拟结果产生影响，其中纵波速度的影响最大，横波速度的影响次之，密度的影响较小。

由于在实际地层中速度和密度并不是单独变化，为了进一步探究非各向异性参数的随机变化对随机正演的影响程度，在各向异性参数ε(图6a、图7a、图8a)、γ(图6b、图7b、图8b)、δ(图6c、图7c、图8c)分别设置为均值为0.1，标准差为0.01 的正态分布的基础上，将地层的速度和密度按照表2(模型1—模型4)设置为不同标准差的正态分布，采用Monte Carlo 随机方法产生满足条件的随机模型，利用Ruger 近似式正演其叠前AVAZ 地震响应，生成椭圆扁率B/A与各向异性因子B散点图(图6—图8)。其中，图6 为上层介质的速度与密度按照模型1—模型4 设置为不同标准差的正态分布，下层介质的速度与密度设置为恒定的均值；图7 为下层介质的速度与密度按照模型1—模型4 设置为不同标准差的正态分布，上层介质的速度与密度设置为恒定的均值；图8 为上、下两层介质的速度与密度均按照模型1—模型4 设置为不同标准差的正态分布。

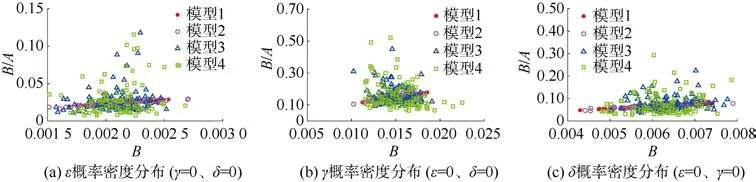
图6 不同标准差的速度与密度模型B/A(椭圆扁率)与B(各向异性因子)散点图(上层介质速度与密度均随机变化)Fig.6 B/A and B scatter plots for velocity and density models with different standard deviations (upper layer velocity and density are set to a normal distribution)

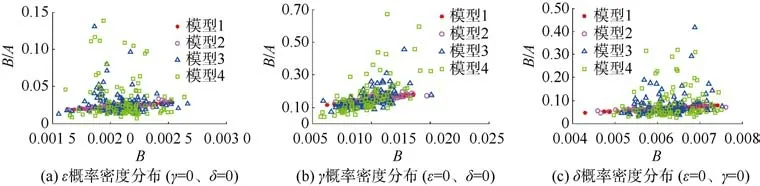
图7 不同标准差的速度与密度模型B/A(椭圆扁率)与B(各向异性因子)散点图(下层介质速度与密度均随机变化)Fig.7 B/A and B scatter plots for velocity and density models with different standard deviations(The velocity and density settings of the upper layer are randomly distributed)

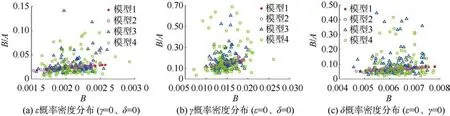
图8 不同标准差的速度与密度模型B/A(椭圆扁率)与B(各向异性因子)散点图(两层介质速度与密度均随机变化)Fig.8 B/A and B scatter plots for velocity and density models with different standard deviations (both the velocity and density of two-layer medium change randomly)

在图6—图8 中均可看出：速度与密度设置为均值时(模型1)，其椭圆扁率的变化完全是由各向异性参数的随机变化所引起，由于模型2—模型4 的速度与密度设置为正态分布，其拟合的椭圆信息的变化是由岩性参数和各向异性参数共同变化所引起的结果。分别将模型2—模型4 与模型1 对比分析：速度与密度在较小的范围内(模型2)随机取值时，模拟出的椭圆信息可以很好地反映裂缝的信息；速度与密度的标准差分别为均值的5%和2.5%时(模型3)，模拟出的散点图基本可以反映裂缝的信息；但当速度与密度的标准差分别为均值的 10%和 5%时 (模型4)，椭圆信息很大一部分受到速度和密度随机波动的影响，其散点分布较为离散。

对比图6–图8 可以看出，两层介质(图8)的速度与密度均为正态分布，比仅上层介质(图6)或仅下层介质(图7)的速度与密度为正态分布时所模拟出的椭圆扁率B/A与各向异性因子B散点图更离散，由于样本值满足正态分布，其值大部分仍然分布在均值附近，所以其散点密集区基本一致。图6—图8 中间一列的b 图为各向异性参数γ设置为概率密度分布，其B/A与B散点分布范围最广；图6—图8 左侧一列的a 图为各向异性参数ε设置为概率密度分布，其椭圆扁率B/A与各向异性因子B散点图分布范围最小；图6—图8 右侧一列c 图为各向异性参数δ设置为概率密度分布时，其椭圆扁率B/A与各向异性因子B散点图分布范围介于a 图和b 图之间。分析得出如下结论：

a.两层介质的速度与密度均设置为正态分布，较单层介质(上层介质或下层介质)的速度与密度正态分布对椭圆扁率B/A与各向异性因子B散点图影响更大。

b.无论是储层还是盖层，由横向岩性变化大而引起速度与密度的随机变化时，椭圆的扁率B/A与各向异性因子B的变化范围均会变大。当横向岩性变化过大即速度与密度随机波动过大(例如模型 4 的速度随机变化范围是其平均值的10%，密度随机变化范围是其平均值的 5%)，会无法准确识别出由各向异性所引起的变化。在不同岩性的裂缝性储层中，地层的横向岩性变化较小时即速度与密度随机变化范围在较小的范围内(标准差小于均值的10%)才能较好地利用该技术评价裂缝。

3 结论

a.以含EDA 介质的双层模型为基础，将Ruger近似式中的各向异性参数和岩性参数设置为正态分布，通过Monte Carlo 随机方法进行叠前AVAZ 正演模拟拟合椭圆信息，分别分析了各向异性参数和岩性参数的随机变化对拟合的椭圆的扁率B/A和各向异性因子B产生影响。模拟实验结果得知，在利用AVAZ 技术评价HTI 介质中裂缝发育程度时，不仅各向异性参数ε、γ和δ会对AVAZ 响应拟合的椭圆扁率B/A和各向异性因子B产生影响，而且非各向异性参数如地层的速度和密度(尤其是地层的纵波速度)的随机变化也会对拟合的椭圆扁率B/A和各向异性因子B造成一定的影响。

b.各向异性参数γ对椭圆扁率B/A和各向异性因子B的影响最大，δ次之，ε最小。非各向异性参数对椭圆扁率B/A和各向异性因子B的影响程度依次为，纵波速度最大、横波速度次之，密度最小。因此，纵波速度的不确定性是造成AVAZ 的响应特征分布的主控因素，横波速度的影响也较大，密度的影响较小。当速度和密度的随机波动范围过大时，与理想的仅考虑各向异性参数变化的模型结果差别较大，所以当速度与密度在较小的范围内随机取值时，椭圆扁率B/A和各向异性因子B才可以较好地反映地层各向异性的强弱即裂缝的密度大小。

c.应用叠前纵波方位各向异性检测储层裂缝时，应当充分考虑地层速度和密度横向的变化对AVAZ 响应特征分布的影响。在具体的实际资料分析中，为了减少地层速度、密度参数对预测结果的影响，在叠前三参数反演得到空间的纵横波速度、密度的基础上，下一步可研究如何利用空间的纵横波速度、密度来提高椭圆扁率的计算精度，进而提高该参数预测裂缝信息的准确性。