铁路钢箱梁正交异性桥面加劲肋疲劳性能研究

蒲黔辉 陈良军 施 洲 洪 彧

(西南交通大学 土木工程学院,四川 成都 610031)

正交异性钢桥面板在国内外广泛应用,并已有许多与疲劳性能相关的研究与试验工作,但研究主要集中于公路车辆荷载下的疲劳性能[1-4],而针对铁路荷载下正交异性钢桥面板疲劳特性的研究较少[5]。京沪高速铁路南京大胜关长江大桥[6]和京沪高速铁路济南黄河大桥虽然采用了正交异性钢桥面板,但属于板桁组合桥面体系,以第二体系、第三体系受力为主。宁波甬江桥特大桥是铁路大跨度钢箱混合梁斜拉桥,固定的铁路行车轨道、更重的轮轴荷载使得正交异性钢桥面的疲劳荷载作用与公路桥、板桁结合桥面和K 撑组合桥面都不同。在针对大跨度铁路钢箱梁正交异性钢桥面研究极少的背景下,疲劳开裂问题应当引起高度重视,通过理论研究与模型试验相结合,研究大跨度铁路钢箱梁正交异性钢桥面板在列车荷载作用下的疲劳性能是具有重要的科学理论意义和工程现实意义。

目前,已有许多关于正交异性桥面板结构的疲劳研究,Xiao等[7]对加劲肋与顶板焊接点进行应力分析发现,增大荷载横向分布面积或增大板厚都可以减小疲劳应力;Aygül[8]采用先进的缺口应力法计算分析正交异性板结构各疲劳细节处疲劳应力,结果较好;陶晓燕[9]认为开口肋横隔板开孔形式对整体应力影响不大,但对局部应力影响显著;苏庆田等[10]利用混合有限元方法对带纵肋钢箱构件进行了局部受力分析;陈红等[11]对大跨度扁平钢箱梁斜拉桥多种形式的横隔板局部应力进行了分析。正交异性钢箱梁是典型的薄壁杆件结构,即杆件在一个方向上的尺寸远小于另外两个方向的尺寸[12]。薄壁杆件分析理论主要有弹性分析理论[13]、能量变分理论[14]、数值分析理论[15]三类方法,其中薄壁杆件弹性分析理论中最经典的理论是弗拉索夫理论,其主要思想是把复杂板壳简化为杆件进行求解,此理论在分析过程中忽略了剪切变形的影响[13]。目前,弗拉索夫理论已被广大学者认可并成为薄壁杆件研究的基础理论之一,之后许多学者在此理论基础上进行补充、扩展,使弹性分析理论更精确、更合理以及应用范围更广泛。正交异性桥面板结构疲劳应力分析是进行疲劳寿命评估的前提,因此准确评估正交异性桥面板局部疲劳应力十分重要。由于模型试验费时费力,目前大部分试验研究都仅针对单一纵肋形式下结构的疲劳特性,不同纵肋形式下的对比研究较少,而在正交异性钢桥面板疲劳开裂问题中,加劲肋是关键构造之一,因此本文将对铁路荷载作用下钢箱梁正交异性桥面板不同纵肋形式下的疲劳特性进行对比研究,研究其疲劳破坏规律和机理。

1 基于弗拉索夫理论的OSD 钢桥面加劲肋局部应力解析理论

1.1 弗拉索夫薄壁杆件空间应力分析理论

基于弗拉索夫理论的薄壁杆件弯曲和自由扭转时的基本假设有:(1)材料为线弹性、匀质、各向同性的假设;(2)小变形假设;(3)弯曲分析时横截面符合平截面假设;(4)自由扭转时横截面周边投影不变形假设,见图1。薄壁杆件结构空间应力分析时应确定其坐标系方向,坐标系定义见图2。

利用弗拉索夫理论求解剪应力时,剪应力在横截面的分布规律有如下两个假设:(1)由于壁厚较小,沿周边切线方向的剪应力在厚度方向上均匀分布;(2)由于壁厚较小,沿周边法线方向的剪应力为0。因此可得,弗拉索夫理论中开口薄壁杆件的截面弯曲分布剪力qb为

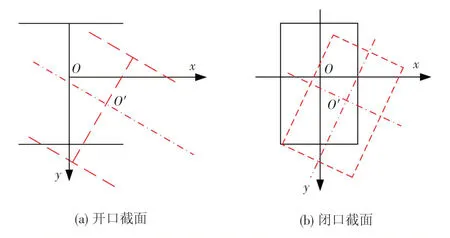
图1 周边投影不变形假设

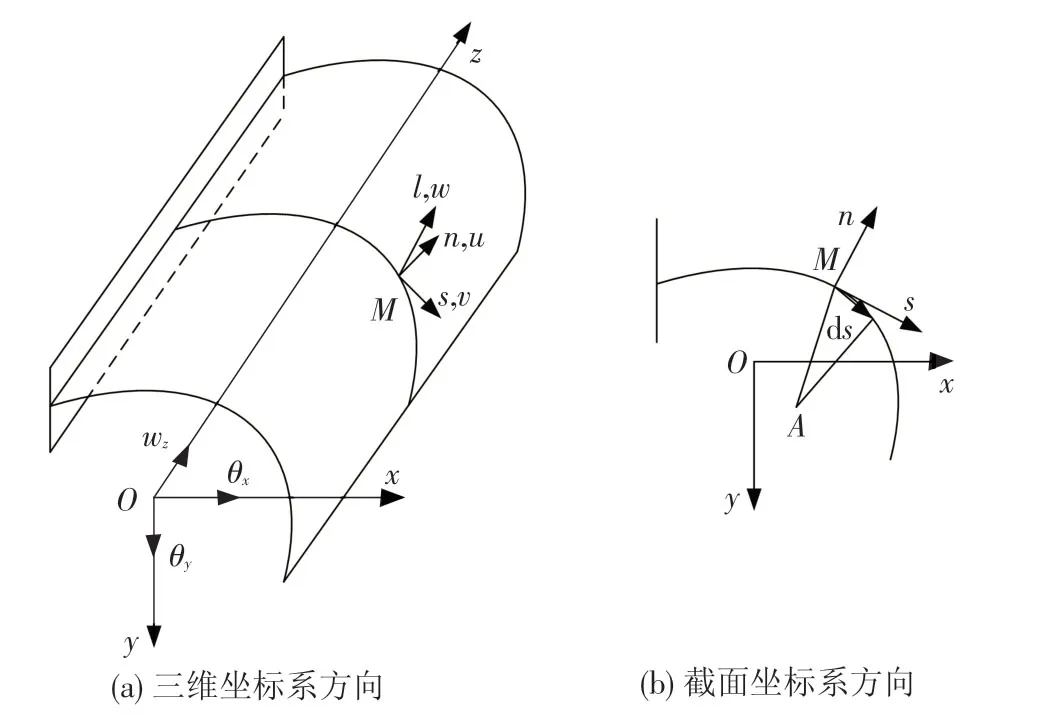
图2 坐标系方向

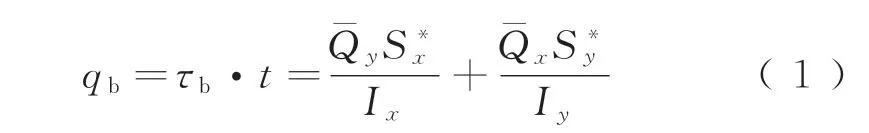
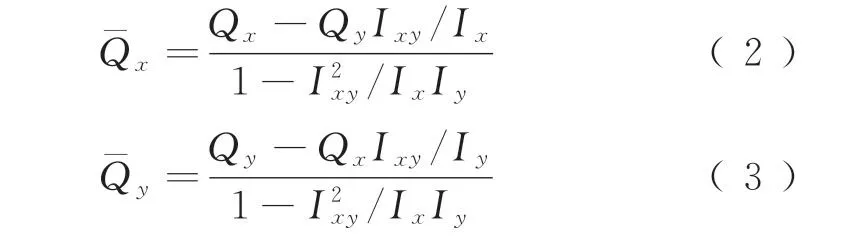
式中:Qx、Qy分别为x、y方向截面剪力大小;S*x、S*y分别为x、y轴截面静面矩;Ix、Iy分别为x、y轴截面抗弯惯性矩;Ixy为x、y轴截面惯性积;t为腹板厚度;τb为截面弯曲剪应力。

1.2 基于弗拉索夫理论的正交异性桥面加劲肋空间应力分析

目前,我国桥梁疲劳规范远不能满足正交异性钢桥发展的需要,对正交异性钢桥面板疲劳敏感部位进行疲劳强度验算时,大多参考国外相对成熟的AASHTO、Eurocode和日本等规范,并采用有限元仿真分析及模型试验的方法验证。而在有限元模拟及模型试验中,通过对加劲肋与横隔板连接处附近测点应力分析和疲劳裂纹进行分析,均发现加劲肋与横隔板连接部位为关键的疲劳敏感细节之一。因此,选取加劲肋与横隔板连接焊缝端部焊趾处(下文统称此处为疲劳敏感部位)进行研究,利用力学分析结合有限元模拟推导加劲肋与横隔板连接处疲劳敏感部位面内疲劳应力的解析表达式,分析不同加劲肋结构形式对该疲劳敏感部位的面内疲劳应力的影响规律和作用机理。

为了分析不同结构形式加劲肋与横隔板连接处疲劳敏感部位的面内疲劳应力影响因素,首先作如下假设:(1)U肋与V肋对顶板的抗弯惯性矩相等;(2)两种加劲肋形式下横隔板开口形状对加劲肋与横隔板连接处的影响相同。通过有限元计算分析发现,加劲肋上翼缘(顶板)传递剪力作用较小,可以忽略不计,因此在简化计算过程中,假设加劲肋与顶板的剪力全部由加劲肋腹板承受,见图3。因此加劲肋腹板可视为一个薄壁杆件,加劲肋与横隔板连接焊缝两侧加劲肋腹

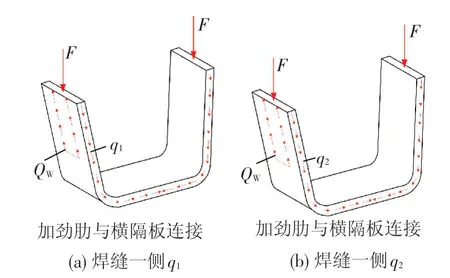
图3 加劲肋受剪示意

板上的剪力流为

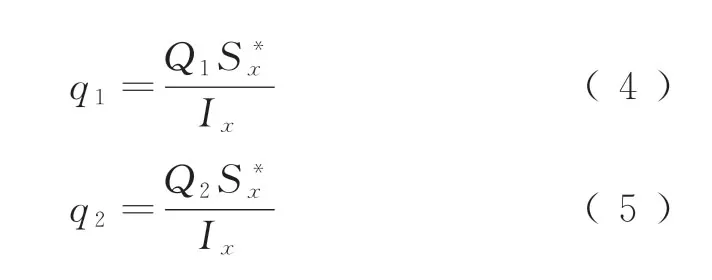
且

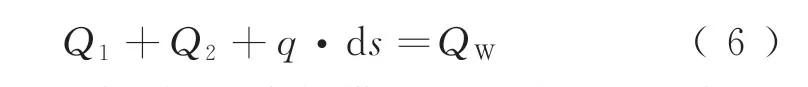
式中:Q1、Q2分别为加劲肋与横隔板连接焊缝两侧加劲肋上的剪力,N;ds为隔离体纵向长度;QW为加劲肋与横隔板连接焊缝作用力的竖向分量;截面静面矩计算公式为

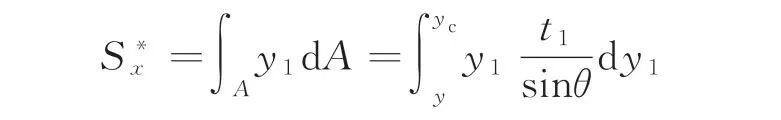
其中,θ为加劲肋腹板与顶板的内夹角(锐角);t1为加劲肋板厚,mm;yc为加劲肋形心位置到最上缘的垂直距离,mm。

再截取局部作静力平衡分析,见图4,利用竖向平衡条件可得

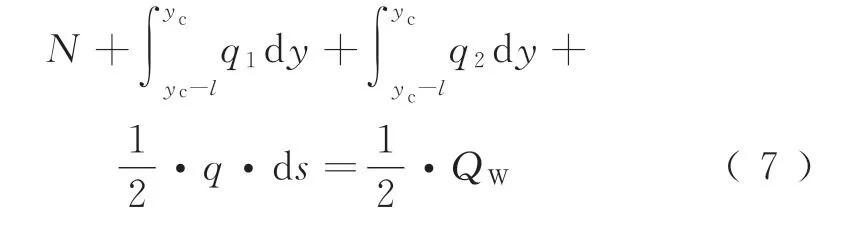
图4 加劲肋局部受剪示意

将式(4)～式(6)代入到式(7)中简化可得,加劲肋与横隔板连接处焊缝端部疲劳敏感部位面内疲劳应力大小为

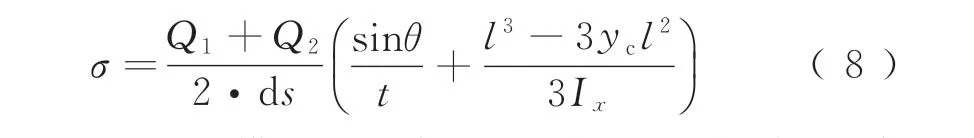
式(8)表明:横隔板两侧剪力、焊缝长度、加劲肋腹板倾角(锐角)、加劲肋抗弯惯性矩、加劲肋板厚等参数是加劲肋疲劳敏感部位面内疲劳应力的重要影响因素,其中:(1)横隔板两侧剪力是最重要的影响因素,减小横隔板间距能大幅降低加劲肋疲劳敏感部位面内疲劳应力,能显著提高此处的疲劳性能;(2)加劲肋疲劳敏感部位面内疲劳应力随着加劲肋与横隔板连接焊缝长度的增加而降低;(3)加劲肋疲劳敏感部位面内疲劳应力随着加劲肋腹板倾角(锐角)的减小而降低;(4)加劲肋疲劳敏感部位面内疲劳应力随着加劲肋抗弯惯性矩的增加而降低。

2 甬江桥工程概况及试验模型

2.1 工程概况

甬江特大桥结构设计新颖,具有独创性,是新建宁波铁路枢纽北环线最大的控制工程。甬江桥钢箱梁采用闭口流线型正交异性桥面板,梁高度为5 m,梁宽度为21 m,在纵向上每3 m 设置一道横隔板。考虑试验场地与设备、加载和测试简便性、加工制造等疲劳模型试验设计因素,并根据甬江桥正交异性桥面板的具体情况,采用通用有限元软件Ansys建立主跨钢箱梁梁段的三维板壳理论模型,对各疲劳敏感部位的疲劳受力特性进行了深入的研究,通过对多种疲劳试验模型方案的结构形式和细部设计进行对比分析的基础上,最终疲劳试验模型见图5。

2.2 试验模型

模型试验方案最终采用足尺节段模型,板件厚度与原桥正交异性桥面板结构完全一致。该试验模型的总体长度为6 000 mm,宽度为3 000 mm,高度为1 386 mm,在纵向上设置两个横隔板,在横向上设置四个加劲肋(包括2条U型加劲肋和2条V型加劲肋,板厚为10 mm),U、V型加劲肋肋的构造参数见表1,把U型加劲肋与V型加劲肋设置在一个模型中,这样便于同时测试,且可以更好更便捷地对两种加劲肋的受力特性和疲劳性能进行对比,同时该模型方案用钢量较小,节约了试验成本,最后设置必要的构造措施,在模型的边横隔板上分别设置人孔,方便试验测试和观察。

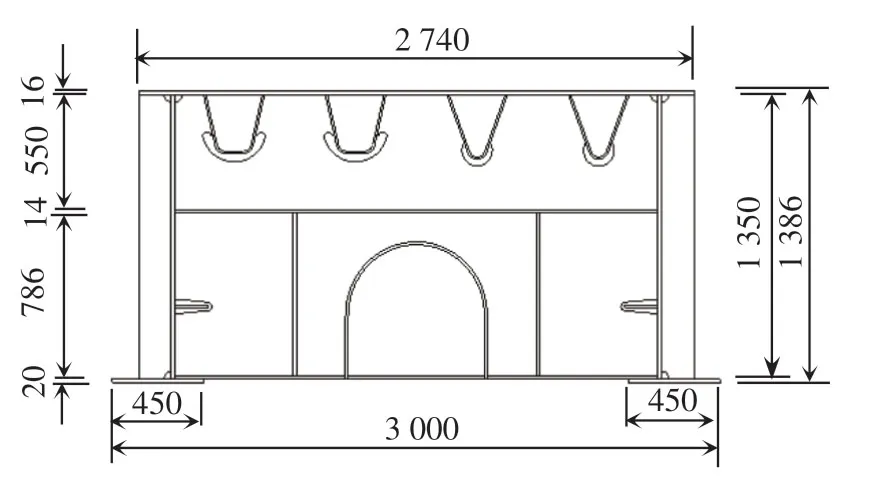
图5 模型侧面(单位：mm)

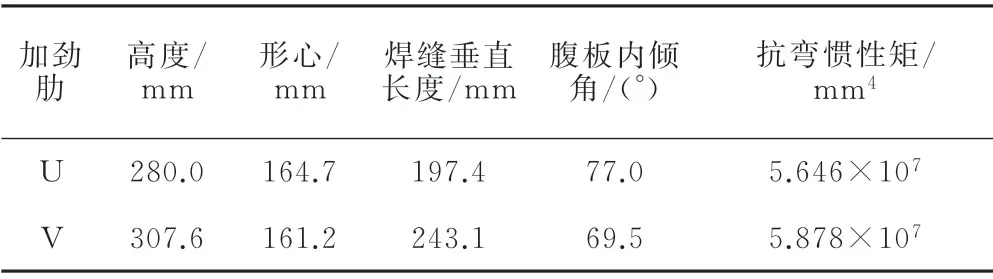
表1 U、V肋构造参数

试验模型安装完毕后,首先对模型进行预加载,使模型各部分接触良好。本疲劳模型试验着重考察加劲肋与横隔板连接部位、加劲肋与顶板连接部位、横隔板开孔处等[16-18]容易发生疲劳裂纹处,根据疲劳试验要求以及本文关注重点,加劲肋与横隔板连接疲劳敏感部位测点布置情况见图6,U肋上U1L、U1R、U2L、U2R 测点分别对应V肋上的V1R、V1L、V2R、V2L测点。

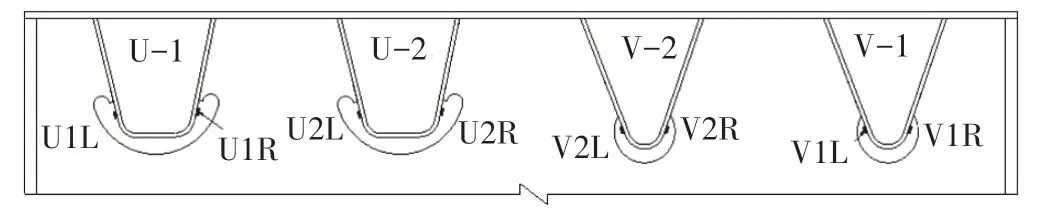
图6 正交异性板加劲肋疲劳敏感部位测点布置

3 正交异性钢桥面加劲肋疲劳特性对比分析

3.1 正交异性钢桥面加劲肋有限元分析结果与解析解对比分析

有限元模拟是疲劳试验模型设计的重要组成,也是模型试验结果验证的有效手段。因此采用通用软件Ansys对模型5进行全面细致地有限元模拟,其中正交异性桥面板结构中钢板部分采用壳单元Shell63进行模拟,桥面板结构中道砟、轨枕和混凝土部分则采用实体单元Solid45进行模拟,桥面板结构中行车轨道采用梁单元Beam4进行模拟,各部分之间的相互作用通过节点耦合实现接触分析,各部分材料参数按实际取值,有限元模型见图7。

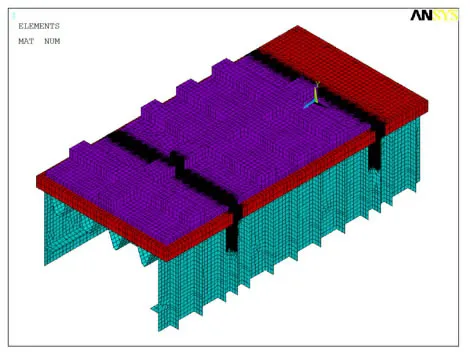
图7 有限元模型

根据产生疲劳裂纹的不同成因,正交异性钢桥面板的疲劳裂纹分为面内荷载引起的开裂和面外变形引起的开裂[16],因此在有限元计算以及试验结果中,加劲肋与横隔板连接焊缝处应力包含了面外应力和面内应力,表2中列出了加劲肋疲劳敏感部位面内疲劳应力解析解和有限元计算值。

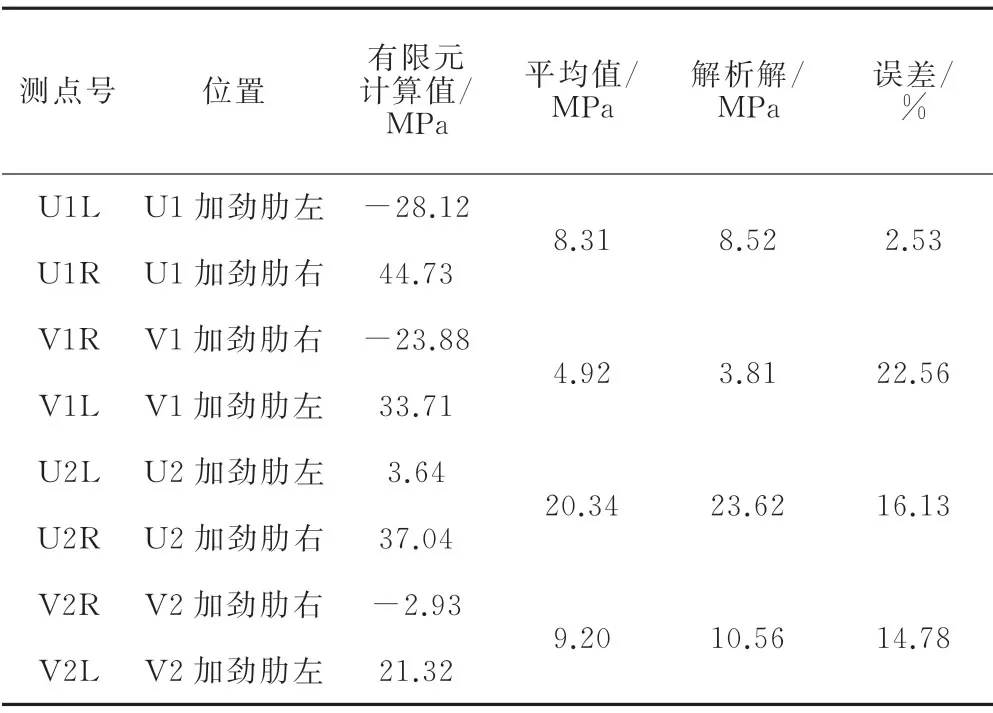
表2 U、V肋疲劳敏感部位有限元计算值和解析解对比

研究结果表明:(1)加劲肋疲劳敏感部位面内疲劳应力解析解与有限元一致,均表现为U肋大于V肋;(2)加劲肋疲劳敏感部位面内疲劳应力解析解有一定的精度,V1加劲肋下误差最大,为22.56%;(3)1加劲肋疲劳应力均各自小于2加劲肋,即外部加劲肋疲劳应力小于中间加劲肋。

3.2 正交异性钢桥面加劲肋模型试验结果与解析解对比分析

疲劳试验研究是评估正交异性桥面板结构疲劳性能以及揭示结构疲劳机理的重要途径。本疲劳试验过程及静载试验均采用MTS 进行加载,在疲劳试验分别加载至1、2、5、10、50、100、200、300、400、420、440、460、480、500、520、540、560万次后进行静载试验,根据Miner疲劳累计损伤理论计算可得,400万次之前疲劳荷载上下限分别为619.365 k N和41.31 k N,400万次后疲劳荷载上下限分别为732.87 k N和41.31 k N。在疲劳试验过程中,试验模型测点应力直接反应了结构的整体受力、传力情况,限于篇幅限制,这里仅列出了加劲肋与横隔板连接焊缝端部焊趾处U2R、U1R 号测点应力随疲劳荷载次数的变化情况,疲劳应力变化规律见图8。

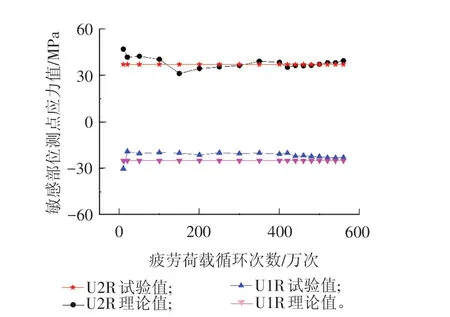
图8 U2R及U1R疲劳测点应力变化

模型试验测试结果与解析解对比见表3。

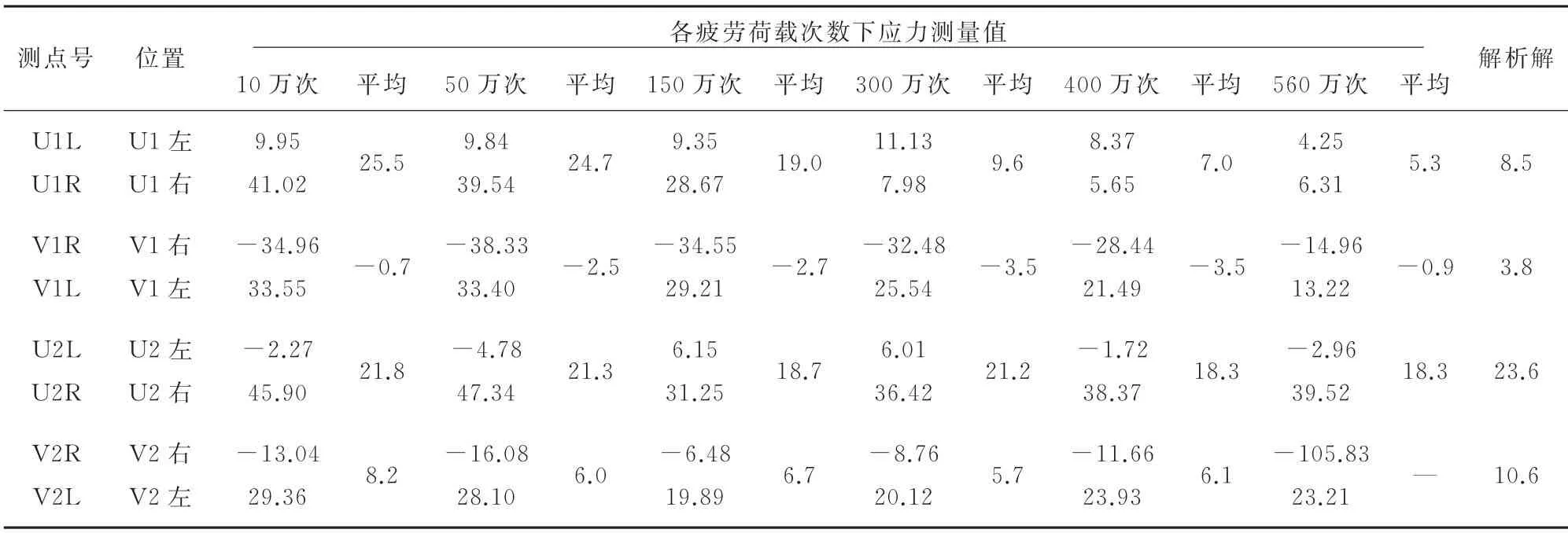
表3 试验测试结果同解析解对比 MPa

研究结果表明:(1)在10万次疲劳加载后对模型进行调整,模型测点的测试值和计算值基本吻合,证明疲劳试验模型结果可以反映原桥结构的受力状态。并且在静载测试中各测点应力随荷载增加呈线性增加状态,因此试验结构在560万次疲劳循环内始终处于弹性范围内工作;(2)在大多数情况下,V型加劲肋疲劳敏感部位承受的应力小于U型加劲肋;而表中V型加劲肋疲劳敏感部位应力大于U型加劲肋的情形,是由于此处U型加劲肋下疲劳敏感部位测点出现裂纹,引起了该处应力重分布导致的;(3)通过对模型试验测试结果与解析解对比分析发现,U2、V1、V2加劲肋疲劳敏感部位面内疲劳应力解析解同试验结果一致,具有较好的精度;U1加劲肋疲劳敏感部位面内疲劳应力解析解误差较大,这是由于该处出现裂纹应力重分布导致的。

3.3 正交异性钢桥面U、V型加劲肋疲劳特性对比研究

U、V肋疲劳敏感部位试验测试结果对比分析情况见表4,U2、V2加劲肋疲劳敏感部位试验测试数据对比曲线,见图9,并结合解析公式及有限元模拟进行综合分析和判断,综合对比研究发现:(1)解析公式、有限元模拟以及试验测试结果一致,由分析可知,大多数情况下,都表现出U肋疲劳敏感部位疲劳应力大于V肋对应部位疲劳应力;对V肋疲劳应力大于U肋疲劳应力的疲劳敏感部位进行观察发现,此处U型加劲肋已出现裂纹;(2)在疲劳试验过程中,利用无损探伤工具对加劲肋结构进行裂纹观察,发现疲劳加载到150万次时,U1加劲肋疲劳敏感部位出现裂纹;(3)综上所述,在铁路列车荷载作用下,针对加劲肋疲劳敏感部位,V型加劲肋比U型加劲肋表现出了更好的抗疲劳性能。

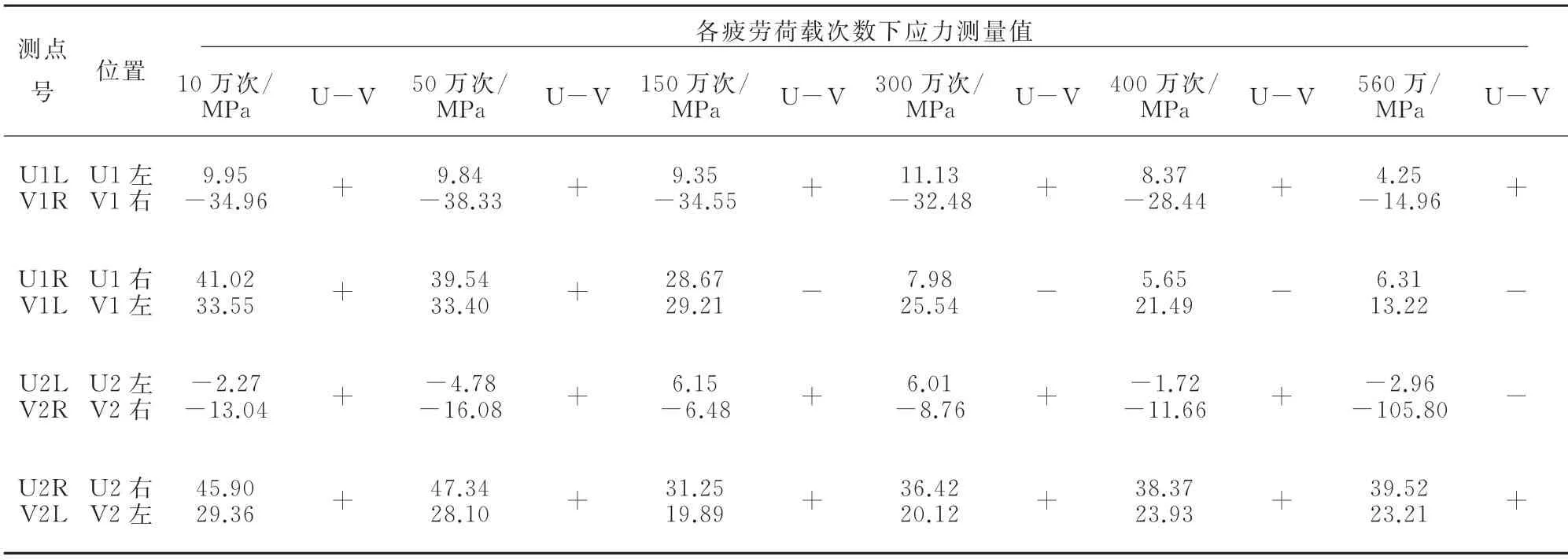
表4 U、V肋敏感部位疲劳试验测试结果对比

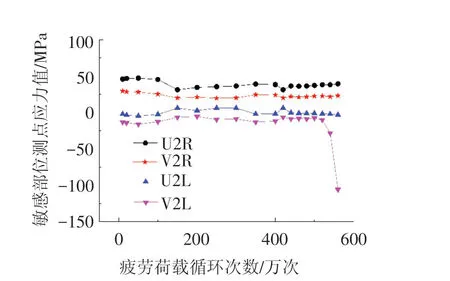
图9 U2、V2加劲肋疲劳敏感部位试验测试数据对比

疲劳模型试验与有限元模拟虽然都能表现出结构的受力及传力机理,且能够直接对比分析不同加劲肋疲劳受力情况,但是各疲劳影响因素的影响程度及作用机理并不明确,而基于力学原理的解析公式便能解决该问题。加劲肋疲劳敏感部位面内疲劳应力解析式即式(8)表明:(1)加劲肋与横隔板连接处焊缝端部疲劳敏感部位面内疲劳应力与该处两侧剪力直接相关,减小横隔板两侧剪力是降低该处面内疲劳应力最根本的方法,因此减小横隔板间距能显著提高结构的疲劳性能,但也势将增加成本;(2)焊缝长度是加劲肋与横隔板连接处焊缝端部疲劳敏感部位面内疲劳应力的重要影响因素之一,并且焊缝长度l在小于两倍yc的情况下,其焊缝端部面内疲劳应力随着焊缝长度的增加而降低,这与模型试验以及有限元计算结果一致;(3)另一个重要影响因素是加劲肋腹板倾角,倾角(锐角)越小,面内疲劳应力越小,这也是V肋下加劲肋与横隔板连接部位疲劳性能较好的原因之一,此结果亦与模型试验以及有限元计算结果一致;(4)抗弯惯性矩Ix亦是一个重要的影响因素,通过试算发现,Ix增大的同时其面内疲劳应力将减小,证明了增大抗弯惯性矩Ix的情况下能减小该处面内疲劳应力,这与国内外已有的关于大纵肋的研究结论一致[17],表明增大加劲肋的截面能增强正交异性板的疲劳性能;(5)从式(8)还可以明确得出,加劲肋腹板厚度越大,该处面内疲劳应力越小。

4 结论

(1)目前为止,采用足尺模型试验在同一模型中对两种加劲肋形式下(U型加劲肋与V型加劲肋)疲劳敏感部位的受力性能和疲劳特性进行对比分析研究,节约了试验成本,提高了试验效率,并且能够更好地有针对性地对两种加劲肋形式下疲劳敏感部位的受力性能及疲劳特性进行对比分析。通过实测数据与理论计算比较分析,发现试验模型与原桥结构等效性较好,试验模型能够准确充分地表达出原桥结构的受力模式与性能。

(2)通过对有限元理论模拟以及模型试验实测数据分析均发现,V肋形式下加劲肋疲劳敏感部位的疲劳应力水平较U肋小,并且在150万次疲劳加载完成后,在U型加劲肋与横隔板连接焊缝端部焊趾处发现了裂纹,而V型加劲肋没有发现裂纹。因此,通过模型试验验证表明,V肋形式下加劲肋与横隔板连接焊缝端部敏感部位的抗疲劳性能优于U肋。

(3)提出了加劲肋与横隔板连接焊缝端部疲劳敏感部位面内疲劳应力的解析公式,其结果同有限元模拟及疲劳模型试验实测结果一致。通过对面内疲劳应力计算公式分析发现:焊缝长度、加劲肋腹板倾角以及抗弯惯性矩都将影响加劲肋疲劳敏感部位面内疲劳应力大小,合理的设计可以有效地减小该疲劳敏感部位的面内疲劳应力。

(4)通过对比分析发现,解析理论、有限元模拟以及试验测试结果一致,在铁路列车荷载作用下,针对加劲肋疲劳敏感部位,都表明V型加劲肋的疲劳工作性能优于U型加劲肋。