基于自抗扰控制的高速列车自动驾驶速度控制

连文博 刘伯鸿 李婉婉 刘宪庆 高锋阳 李茂青

(1.兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070;2.西安电子科技大学 机电工程学院,陕西 西安 710071)

随着高速列车的快速发展,原有司机操作加列车防护系统ATP(Automatic Train Protection)监督的运行机制无法保证列车安全快速运行的同时兼顾列车的运行效率。因此向高速列车增加自动驾驶系统ATO(Automatic Train Operation)成为当下研究热点[1],很多学者提出不同的解决方案,但主要从列车建模和列车控制算法着手,列车建模主要有物理建模和系统辨识两种方法,物理建模主要有单质点模型和多质点模型[2],两种物理模型各有优缺点。单质点模型计算量小且控制器设计简单,但未考虑列车与车辆之间的作用力,因此所建模型精确度不足。相比单质点模型,多质点模型提高了模型的精确性,但计算量增加,同时控制过程过于繁琐,不利于控制器的实时输出;针对物理建模存在的问题,衷路生等[3]提出基于极大似然辨识的列车非线性辨识算法,能够避免物理建模的繁琐,但该方法需要对条件数学期望进行梯度搜索,缺乏实时性。目前针对高速列车应用的控制算法主要有模糊控制、预测控制、自适应控制、神经网络控制或多个控制理论的组合[4-7],但这些算法都较难以达到微分控制器PID(Proportion Integration Differentiation)控制设计简单、弱模型依赖的优点,如Cao等[8]提出基于模糊预测控制的列车控制算法,模糊预测控制能够保证列车精确追踪,但是模糊隶属度函数的建立过程复杂,不利于列车的实时追踪;Li等[9]提出基于迭代变参数和测量噪声的自适应迭代学习控制,该方法虽能在线修正控制参数,但对参考模型的依赖性强,不能适应复杂环境的变化;针对上述问题,本文采用对PID控制进行改进的自抗扰控制进行列车速度控制器的设计,并充分利用自抗扰控制对模型精度的弱依赖及对干扰自屏蔽的特点,根据先验知识,选择列车单质点模型中的未知部分作为扩张状态,通过仿真,验证ADRC控制器在列车运行控制系统中的可行性和优越性。

1 列车运行模型

准确描述列车运行模型是合理设计控制器的前提,本文参考文献[10]设计的列车ATO系统结构,见图1。

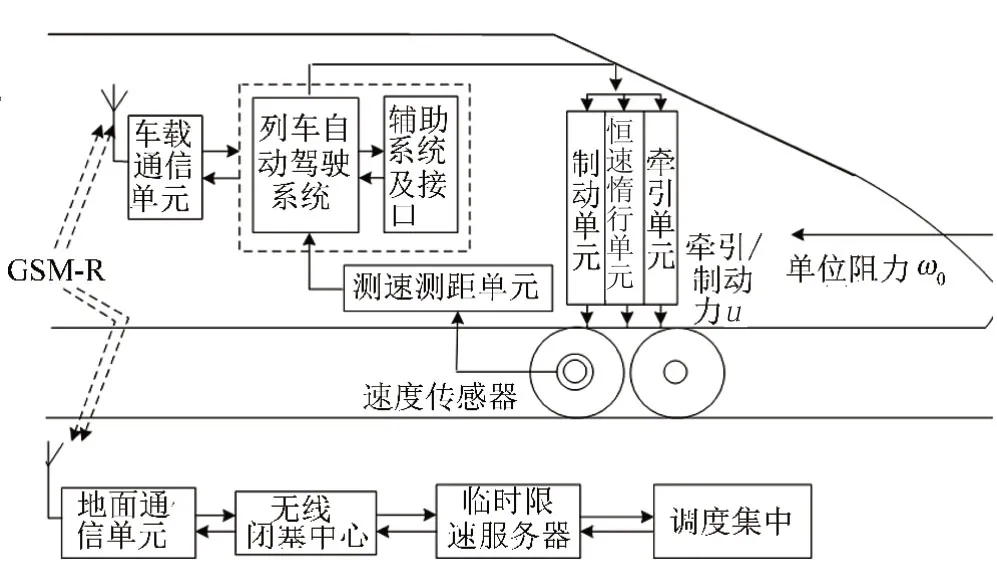
图1 列车ATO结构及受力分析

由图1可见,列车受到单位阻力和牵引/制动力两个力。视列车整体为刚性质点对列车进行力学建模,可得到高速列车单质点模型为

式中:s为位移;v为列车运行的实时速度;u为列车受到的牵引/制动力;ω0为列车所受基本阻力;a、b、c分别为列车滚动机械阻力系数、摩擦阻力系数、空气阻力系数,通常当列车运行速度超过350km/h,空气阻力会占80%以上;ξ为列车加速度系数;γ为列车的车轮回转质量系数,实际运行中,列车的阻力包括附加阻力和基本阻力两部分,基本阻力会受列车速度影响,但附加阻力只在线路固定部分出现[11],为简化仿真过程,本文设定列车在平直线路运行,只考虑基本阻力对列车运行的影响,以上参数除阻力未知外,其余量都可通过测量得到。

根据式(1)的列车模型,建立列车运行状态空间方程

式中:x1为列车位移;x2为列车速度;x2的导数为列车加速度;d(t)为列车受到的干扰。

2 自抗扰控制器设计

PID控制算法具有设计简单、响应迅速的优点,适用于如列车等快速反应系统,但PID存在响应越快速系统越易超调的矛盾,同时,在强干扰作用下,PID易失去稳定性,鲁棒性不强;因此,韩京清[12]提出自抗扰控制算法对PID进行改进,使用微分器对输入进行过渡环节设计,避免输入量直接作用于对象导致输出量超调的现象,同时设计状态扩张观测器(ESO)对状态方程中未知部分进行估计,最后设计非线性控制律NLSEF,并对外界干扰进行补偿,实现精确控制。

2.1 结构

将自抗扰控制应用于列车,设计的二阶自抗扰控制器原理见图2。

图2 二阶自抗扰控制器

图2中,TD表示最速跟踪-微分器,主要用于建立过渡环节,消除PID控制中快速与超调的矛盾,首先将输入v进行非线性微分处理,得到v的过渡值v1和微分值v2,其余e1=v1-z1,e2=v2-z2,b0为补偿因子,决定补偿量的大小;然后将列车中未知的部分设为扩张态x3,利用ESO分别对x1、x2、x3进行观测,观测结果为z1、z2、z3,最后通过非线性控制律计算得到控制量u0,同时根据观测结果添加补偿量1/b0,对控制量u0进行补偿,作用于列车,得到输出速度y,具体步骤为:

Step1过渡环节设计

本文设计非线性微分跟踪器为

式中:v为期望输入;v1为v的跟踪值,同时v1的导数为v2;k为第k时刻;δ为微分器跟踪因子,决定TD追踪v的快慢;h0为滤波因子,能够滤除噪声,因输入期望信号一般无噪声,故一般令h0=h,h为仿真步长;fst(*)为最优控制函数,具体结构为

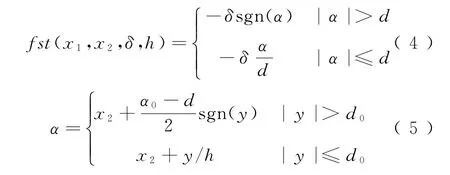
式中:d=δh;d0=hd;y=x1+hx2;α0=

Step2扩张观测器设计

ESO是自抗扰控制算法的核心,主要是通过考虑系统参数跳变、未建模动态及外界干扰对系统的影响,将这些影响视为一个整体作为扩张状态进行观测和补偿操作,进而消除干扰的影响,实现系统无静差控制,对于列车系统首先设扩张状态x3=f,其中f=aξ+bξx2+cξx22,为列车不可知部分。对系统扩张状态x3进行估计,得到z3估计值为

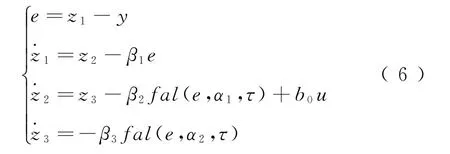
式中:β1、β2、β3为系统增益参数,合理的增益配置会使系统的性能得到改善;根据式(2)可知b=ξ;fal(e,α,τ)为非线性饱和函数,其中τ决定fal(*)函数中非线性区间的宽度,fal(e,α,τ)主要用于抑制信号的抖震强度,定义为

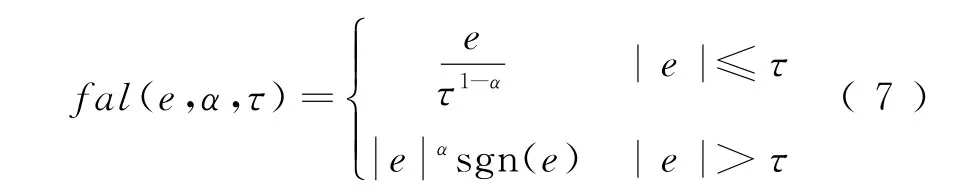
Step3非线性控制律

通常情况下,PID控制采用的控制律是反馈误差的比例、微分、积分三者的线性组合,该控制律结构简单,不能屏蔽系统的干扰,因此本文使用韩京清教授[13]提出的PD形式的非线性组合控制律,得到控制量为

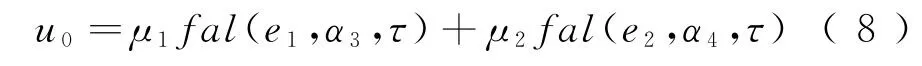
式中:μ1、μ2为增益;e1=v1-z1;e2=v2-z2;fal(*)见式(7),综上可得输入到列车的控制量为

2.2 控制器参数整定

自抗扰控制算法主要是针对PID出现的诸多弊端进行改进,但改善PID控制器性能的同时,增加的非线性反馈律、ESO、TD 过渡环节会使控制参数的数量增多,本文设计的二阶ADRC控制器参数共有13种,因此需要对控制器参数进行合理整定。

(1)TD参数整定

TD 环节中需要调节的参数有式(3)中的δ和h0,δ决定过渡环节追踪的效果,其越大追踪效果越好,跟踪信号越贴近期望信号,但δ过大会导致系统超调,过小无法保证跟踪性能,需要适中选取;δ和过渡时间T存在关系为

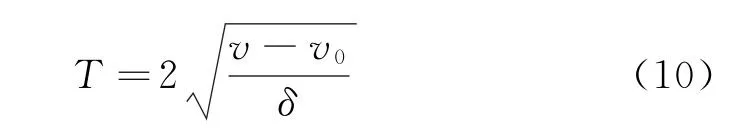
式中:v0为追踪初始值。

(2)ECO参数整定

扩张观测器需要整定的参数共有6个,β1、β2、β3、α1、α2、τ,其中由于τ决定fal(*)函数中非线性区间的宽度,τ过大fal(*)会变成线性函数,失去其非光滑反馈的设计初衷,反之τ过小会使得非线性过强导致系统出现开关现象使系统在原点附近震荡;同时α1、α2过小会产生较大的追踪误差,过大会导致系统震荡,该值决定了系统的跟踪性能,一般取α1=0.5、α2=0.25。

β1、β2、β3作为ESO的增益参数,很大程度上决定控制的性能,该值和仿真步长h有关[14],其中取

(3)NLSEF参数整定

非线性控制律中共有5个参数,分别是式(8)中的μ1、μ2、α3、α4和τ,其中μ1、μ2所起的作用和PD控制中比例和微分系统相同,μ1决定系统的响应时间并具有屏蔽干扰的作用,即μ1越大,响应时间越短,屏蔽干扰的能力越强,同时μ2能够调节系统性能,μ2增大,系统的阻尼会随之增大,能避免系统出现超调,但同时μ1、μ2不宜过大,过大会导致系统震荡,需要适中选择。α3、α4、τ的设置要求和ESO的α1、α2、τ相同,设定α3＜1能保证fal(*)函数的非光滑反馈,α4＞1能保证微分值大时取光滑反馈,本文令α3=0.75、α4=1.5。

3 仿真分析

本文的仿真共分为两部分,首先是利用动车组实际参数进行自抗扰控制器设计及理想曲线追踪;然后建立非线性PID控制器和传统PID控制器,使用相同的列车参数和追踪曲线,比较三者性能差异。

本文选择CRH380A型动车组作为研究对象,具体参数见表1。

表1 CRH380A型动车组参数

本文参考文献[15]设置的理想目标曲线,假定列车运营场景主要由“启动牵引-匀速-制动-匀速-牵引-匀速-制动停车”组成,令T=1 200 s,列车追踪目标速度Vinc=368.34km/h,t1=-160×log2(-200/Vinc),其中T用于时间分段处理,t1为转折时间,具体为

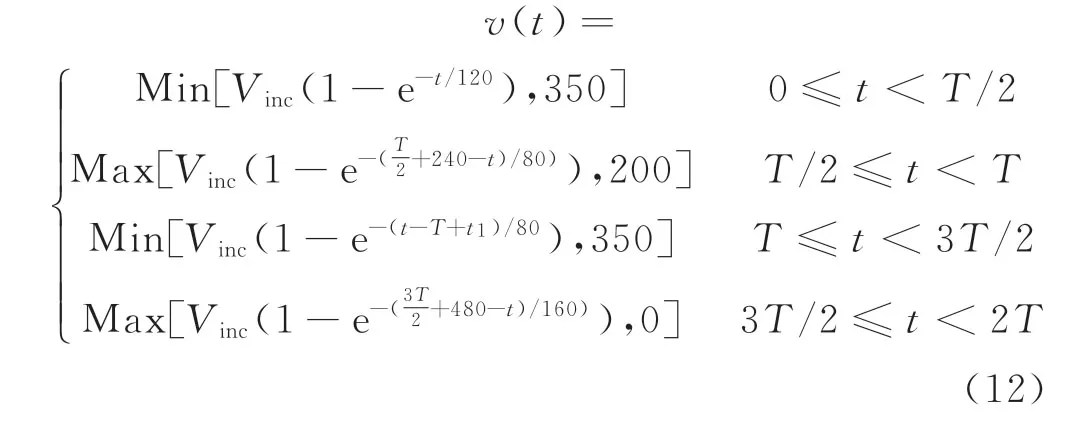
3.1 自抗扰控制器仿真

根据式(2)和CRH380A 动车组参数,可以得到CRH380A 动车组状态空间方程为

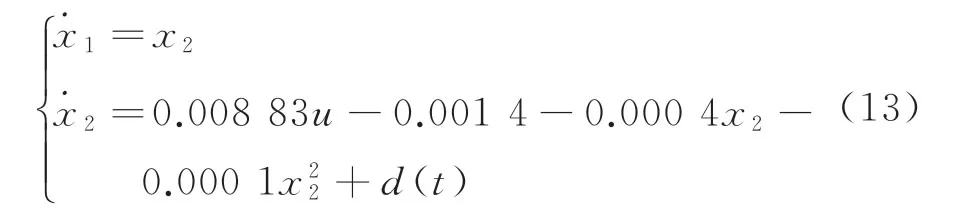
在Matlab2014a平台上进行仿真,使用s函数进行编程,令d(t)=sin(0.77t),其Simlink仿真见图3。

图3 Sim link仿真

图3中,共使用了5个s函数,其中v_input模块为系统期望输入模板,可生成见式(11)的目标追踪曲线,Train模块为高速列车模型模块,采用式(12)的状态空间方程表示列车模型;Evant模块为微分器过渡模块,本文使用了Levant微分器进行TD 设计,参数分别设置为α=1,λ=5;ADRC模块为自抗扰控制器模块,非线性控制器参数为α1=0.75,α2=1.5,δ=0.001,μ1=6 000,μ1=5 500;ESO 模块为扩张观测器模块,设 置β1=1 200,β2=1 700,β3=4 500,δ=0.001,α3=0.5,α4=0.25;设置采样周期(即仿真步长)h=0.001,使用Clock模块计时;首先向v_input模块写入阶跃曲线,设置仿真时间为10 s,观察响应追踪曲线,X和Z为输出模块;K为增益模块;仿真输出速度y阶跃响应见图4。

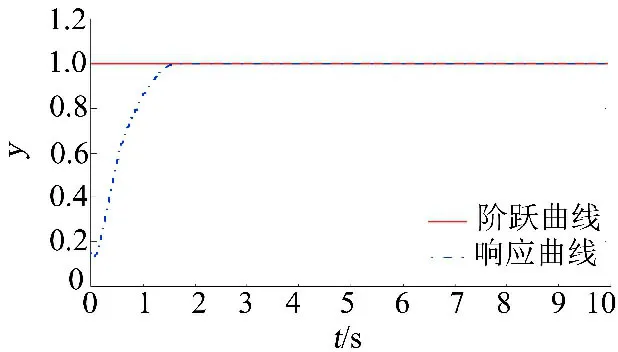
图4 ADRC阶跃响应跟踪曲线

由图4可知,ADRC的追踪性能良好,无超调;进一步目标追踪曲线载入v_input模块,设置仿真时间为2 400 s,其追踪结果见图5,追踪误差见图6。

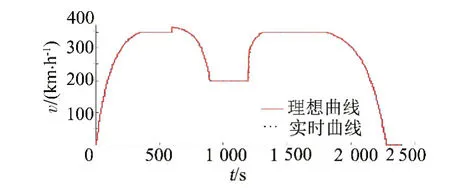
图5 ADRC速度追踪曲线

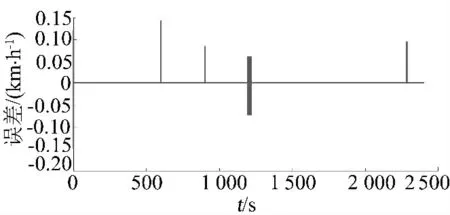
图6 ADRC追踪误差

由图5可见,曲线追踪密贴良好,且没有越过目标曲线,也没有出现系统超调现象,说明ADRC控制器作用下的追踪效果良好,同时由图6可见,追踪曲线的平均误差位于(-0.15,+0.15),列车的追踪误差小于速度的1%,满足列车精确追踪的要求。扩张观测器ESO的观测结果见图7。

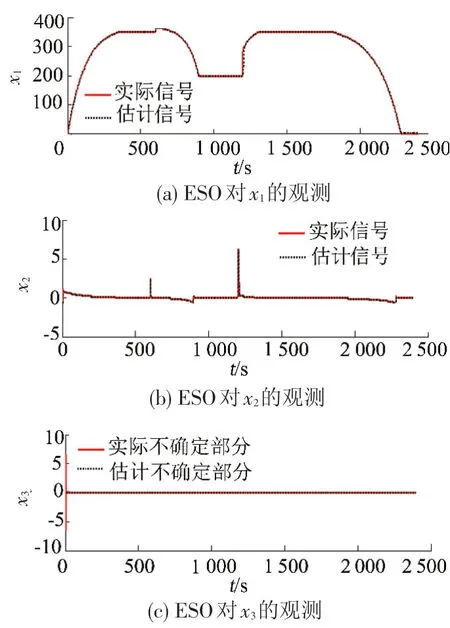
图7 ESO观测结果

图7中x1、x2、x3分别为z1、z2、z3经ESO 观测的结果,如前所述,x1、x2、x3分别令为列车动力学模型中的速度y、加速度dy、未知部分f;图7(a)实际表示ESO 对列车速度y的观测结果z1及实际速度变化,图7(b)实际表示列车加速度dy的变化及其观测结果z2,图7(c)实际表示列车未知部分f的变化及观测结果z3,从图7中可以看出,观测值和实际值相差较小,可以保证控制的精度。

3.2 控制器性能比较

为了证明ADRC在控制精度与抗干扰方面的优势,本文选择传统PD控制和非线性PID作为对比对象,同时载入相同的目标追踪曲线,具体见式(11),设定相同的干扰d(t)=sin(0.77t),比较三者抗干扰性能和追踪误差;首先,设计线性PD控制,其控制律为

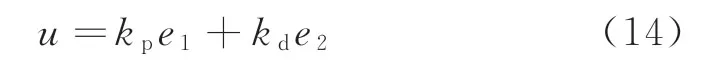
式中:e1=yr-y;e2=dyr-dy;yr为列车目标追踪速度;y为列车实时速度;本文设置kd=1.5,kp=6,控制对象为CRH380A型动车组。

本文也设计了非线性PID控制器,其控制律为

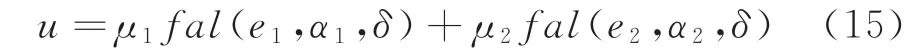
令μ1=6,μ2=1.5,让两类传统控制器对列车目标速度曲线进行追踪,仿真结果见图8。

图8 3种控制器速度追踪对比

图8中,yr为列车目标速度曲线,ypd为传统PD控制得到的追踪曲线,yNPID为非线性控制器得到的追踪曲线,yADRC为自抗扰控制得到的追踪曲线(基本上与yr重合)。PD控制下的追踪曲线波动较大且越过目标曲线,非线性PID作用下的追踪曲线距离目标曲线较远,同时曲线也出现较大波动,但ADRC控制下的追踪曲线基本密贴追踪曲线,既不越过目标曲线也不产生较大波动,由此可知ADRC的控制效果最好,非线性PID控制次之,PD控制最差,为了定量描述,分别求解3个控制器作用下得到的误差值,见图9。

图9 3种控制器的追踪误差

由图9可见,非线性PID控制器和PD控制器的误差呈波浪型变化,且非线性PID控制器的振幅最大达到了28.74km/h,PD控制器的振幅最大达到了59.63km/h,同时ADRC的误差基本呈水平线过零点,追踪误差基本为0,可以实现无静差追踪,具有良好的追踪特性。

为了更加直观的表示列车的追踪效果,比较三者对于给定位移sr的追踪结果,使用目标曲线对给定位移的追踪结果,见图10。

由图10可见,非线性PID和PD控制的位移追踪都存在着较大的误差,相比之下,ADRC的追踪效果就很理想,基本密贴位移追踪曲线,而位移曲线追踪精度可以反映列车的停车精度,可以得出ADRC的停车精度高于传统PD控制和非线性PID。

图10 3种控制器对给定位移追踪

4 结束语

本文针对高速列车传统PID控制器在强干扰作用下稳定性不高、鲁棒性差的缺点进行改进,设计基于自抗扰控制的列车速度追踪算法,同时保留传统PID反应快、设计简单的优点;与传统PD控制和非线性PID控制在速度追踪和位移追踪方面进行比较可以得出,基于ADRC控制器的列车速度追踪算法具有追踪性能好、抗干扰的优点。