轮对系统随机动态分叉研究
2020-04-16朱海燕蒋忠城陈清化
张 波 朱海燕 曾 京 蒋忠城 陈清化
(1.中车株洲电力机车有限公司 试验检测工程中心,湖南 株洲 412001;2.大功率交流传动电力机车系统集成国家重点实验室,湖南 株洲 412001;3.华东交通大学 机电与车辆工程学院,江西 南昌 330013;4.西南交通大学 牵引动力国家重点实验室,四川 成都 610031;5.湖南铁路科技职业技术学院,湖南 株洲 412000)
车辆蛇行运动是轨道车辆独有的现象,由于车轮踏面近似为锥形,轮对运行时会发生横向摆动,同时伴随有绕其质心的垂直轴来回摇头转动,运动轨迹类似“蛇”爬行过程的波形。蛇行运动存在临界失稳点,正常情况下轮对系统会在蠕滑力作用下自动对中,但一旦越过临界失稳点蛇行运动就会失控,轮轨蠕滑力不足以使轮对对中,轮对发生蛇行运动,横向运动加剧,车辆振动平稳性和运行安全性将严重变差,甚至有发生脱轨和翻车的可能,可以说蛇行运动是决定车辆能否高速运行的关键因素。
车辆出现蛇行失稳的临界状态对应的速度称为蛇行失稳临界速度,为了获取准确的临界速度,学者们将稳定性和分叉理论引入蛇行运动问题中,建立了精细化的动力学模型,提出了许多定性以及定量的研究方法。曾京[1]和吕可维[2]分别运用打靶法和延续算法对非线性车辆蛇行运动Hopf分叉现象进行了数值求解,对轮对蛇行运动中的极限环性质进行准确判别,可精准求解出非稳定的虚环,解决了龙格-库塔法求解不稳定极限环的困难。丹麦True[3]教授借助延续算法软件包PATH 对非线性铁道车辆系统的稳定性与分岔问题进行了深入讨论,取得了较为典型的理论性成果。Polach[4]结合铁道车辆蛇行运动理论与试验研究,详细对比分析了几种标准常用的构架失稳评判标准的差异,指出车辆稳定性的计算结果除了依赖于车辆结构参数之外,与轮轨接触关系和数值计算方法也有关联。高学军研究了客车不对称分岔行为[5],创新性地提出“合成分岔图”的概念和构造方法。
但是上述这些研究都是在确定域中进行的,均没有考虑随机激扰的影响,这仅仅是理想情况下的理论分析,判定车辆系统是否失稳通常都是基于系统部件横向振动的衰减特性,但实际车辆线路运行时,由于持续存在随机激扰,车辆振动响应曲线不会出现明显的收敛或发散特征,此时确定性框架下的理论失稳判定方法不再适用,已经不能满足高速车辆的稳定性分析需求。我国对于线路运行过程中的车辆失稳判定方法:对轴箱弹簧正上方对应的构架位置横向加速度进行10 Hz低通滤波,若该横向加速度峰值出现连续6次达到或超过极限值0.8g时,则判定转向架横向蛇行失稳。但这一方法并无理论根据,且由于我国列车运行环境、运行速度与国外的巨大差异,因此并不具备广泛适用性。尽管也有许多学者提出了新的判定方法[6-8],但都有各自的局限性。
大量研究发现,随机激扰和非线性会出现相互耦合关系,两者的耦合效应激发了激扰在非线性系统中的作用,这种作用在系统响应演化过程中具有决定性且不可控。基于这一前提,我们需要跳出稳定域框架,在随机域中寻求新的突破,聚焦于对自然规律的描述更为本质和真实的随机系统,探讨随机激扰对车辆动力学动态行为的影响,从机理上分析车辆随机振动响应,研究随机振动响应的内在非线性特性及变化规律,为轨道车辆系统安全性能设计提供理论指导价值,在高铁全面飞速发展的大背景下,这也是大势所趋。
目前关于车辆随机稳定性的研究较少,比较典型的研究为刘伟渭等[9-10]和张波等[11-13]的研究工作,但这些研究工作都是基于超临界轮对系统,对亚临界系统的随机稳定性并未做研究。本文在此基础上,进一步深入研究随机参激下亚临界和超临界分叉2种轮对系统的随机稳定性及随机分叉,分析随机激扰对稳定性的影响,对比2种类型轮对系统的随机分叉的差异,探讨车辆随机系统的失稳判定方法,研究随机临界速度的计算方法。此外,本文关注的重点在于随机激扰的影响,关于其他车辆参数的影响,已有大量研究,本文不做讨论。
1 悬挂轮对系统随机动力学建模与求解
1.1 模型建立
轨道车辆结构庞大,自由度较多,其非线性问题非常复杂,如果再考虑随机影响,问题的复杂度将剧增。在车辆系统研究过程中,通常根据研究需要对车辆模型进行适当简化,对于重点关注项点精细建模,对于非重点关注项点可做适当简化。为了简化理论研究的难度,本文选取自由度较少的悬挂轮对横向动力学模型来作为分析对象。
建模过程中可作如下基本简化[14]:
(1)构架与轮对之间的耦合效应可忽略,构架的摇头以及侧滚运动对轮对的影响可忽略。
(2)由于轮对侧滚与横移的耦合效应,仅考虑轮对摇头和横移2个自由度。
(3)不考虑轮对柔性,不考虑车轮与钢轨脱离情形。
(4)暂不考虑一系悬挂的非线性特性,仅考虑轮轨间非线性特性。
(5)车轮踏面外形采用经典的锥形踏面。
轮对系统建模时采用Kalker经典线性轮轨蠕滑理论,轮轨非线性接触关系可近似处理为一个非线性五次多项式,对应的2个非线性项系数α1、α2的选取依据来源于文献[14]。车辆系统的随机激扰主要包括随机外激和随机参激,前者主要包括气动随机激扰以及轮轨随机激扰,后者主要是由于自身结构的随机特性引起的激扰。目前商用动力学仿真软件很容易实现外部激扰对车辆稳定性的影响分析,但是关于随机参激激扰的研究则凤毛麟角,商用软件也无法考虑参激激扰的影响,因此本文侧重于研究随机参激对稳定性的影响,且此方法仍然适用于随机外激。
实际车辆中,随机参激也是无处不在的,车辆实际参数值和理论设计值通常会有一定差别,这一差别往往是随机不可控的,而车辆系统一系悬挂参数对运动稳定性的影响较大,因此研究一系悬挂参数的随机变化对车辆稳定性的影响意义重大。
实际上由于材料及结构的制造误差,橡胶元件的老化以及悬挂元件的频变特性都会引起参数的随机变化,由于这些因素具有随机性,无法准确描述其特性。为了描述参数的随机性,通常的做法是结合大批量相应部件试验结果统计分析参数分布规律,这种分布规律通常是参数理论值与一个随机过程的叠加效应,这一随机过程模型就是本文所说的随机参激。铁道车辆轮轨随机激励属于强随机激扰,主要呈现非高斯分步,而车辆一系悬挂参数的随机激扰相对较弱且接近于高斯分布,因此工程分析时可近似处理为高斯白噪声随机激扰。这种方法有两大优势:(1)可直接应用成熟的高斯白噪声数学理论;(2)高斯白噪声数学模型有利于理论分析,简化理论分析难度。因此,本文选取高斯白噪声经典随机过程来模拟轮对系统的一系随机参激,高斯白噪声的最鲜明特点是功率谱密度为常数且功率是无穷大。轨道车辆轮对系统摇头和横移耦合的随机几何模型示意图见图1。

图1 轮对几何模型示意
相关函数为

式中:v为车辆运行速度;ξ(t)为高斯白噪声随机参激激扰,该随机过程均值为0;2D为强度。
由图1关系,可建立轮对横移和摇头运动耦合方程。
(1)轮对横移运动

(2)轮对摇头运动

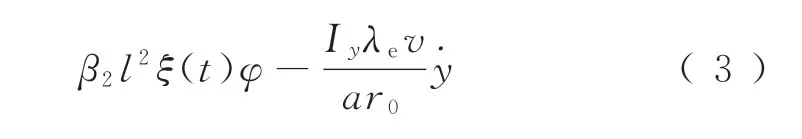
轨道车辆及轮对系统中的Hopf分叉有2种常见类型:超临界和亚临界分叉,为了研究这两类系统的随机动力学行为差异,分别选取2组轮对系统参数作为代表,各参数取值及物理意义详见表1。关于随机项控制系数β1和β2的选取,实际应用时可以通过部件大批量抽样试验统计激扰的能量来确定控制参数,本文的参数取值仅仅只是一个示例,并不精确。

表1 两类轮对系统参数
上述轮对系统的运动方程表示成矩阵形式,即

式中:


1.2 轮对系统的随机平均求解
方程(4)是随机微分方程,其求解比较复杂,许多学者针对具体问题提出了相应的求解方法[15]并取得了很好的效果,但都不具备很好的推广性。相对来说,随机平均法应用最为广泛,随机平均法实际上是随机意义上的Krylov-Bogoliubov-Mitropolsky(以下简称KBM)渐近法,许多学者进行了大量关于随机平均法的研究,最为典型的就是浙江大学朱位秋院士的成果,朱院士在Hamilton框架下建立了一套完备的拟Hamilton系统的随机平均法理论体系[16],可快速求解非线性系统的随机响应,进而分析随机稳定性与随机分叉等问题。
相比于能量和位移幅值,位移和速度随时间的变化速率明显更快,也就是说能量和位移幅值属于慢变过程,而速度和位移属于快变过程。由于慢变过程体现了系统长时间历程内的性态,在研究中应重点关注。随机平均求解的基本原理就是将快变过程随时间变化的特性在时间域进行平均,从而将系统简化为关于慢变过程的随机平均方程。随机平均法主要有以下两大优势:(1)可对系统降维简化问题的复杂度;(2)系统降维简化信息不失真,可保留原系统的主要非线性特性。本文通过随机平均法将轮对横向位移和速度等快变过程组成的多维空间域映射成关于系统能量等慢变过程的一维域。
取广义位移q1=y,q2=φ,p1=,p2=,将轮对运动方程转化为如下形式


该轮对系统中,由于陀螺力[17]的存在,导致轮对系统变为非保守系统,鉴于陀螺项的反对称性,可取系统的Hamilton函数为

式中:H为对应轮对系统的广义能量。
依据随机平均法,式(6)可转化为Itô(伊藤)随机微分方程

式中:odB(t)表示随机积分,且

根据Hamilton系统理论分类[18],该轮对随机系统属于拟不可积Hamilton系统,利用拟不可积Hamilton系统随即平均法对位移和速度等快变过程进行随机平均,可得关于慢变过程能量H(t)的Itô随机平均微分方程

式中:
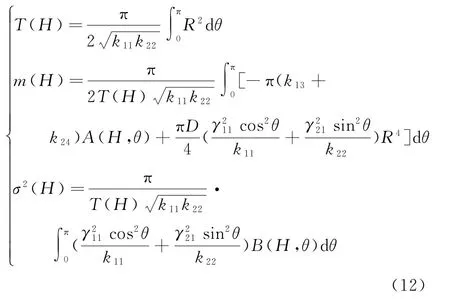
其中,

且R满足

2 轮对系统的随机稳定性与随机分叉
2.1 轮对系统Hopf分叉
当不考虑随机激扰时,即轮对系统(4)中随机项满足R=0。本文根据表1中的参数采用打靶法[1]分别求解两类轮对系统横向位移的Hopf分叉及极限环。为研究系统长时间历程内的性态,通常做法是关注慢变过程——轮对横向振动位移幅值随速度增大过程中的变化情况,画出Hopf分叉图,见图2。

图2 轮对系统Hopf分叉
轮对系统发生了亚临界Hopf分叉见图2(a),系统既出现了Hopf分叉(Hopf分叉点A)也出现了鞍结分岔(鞍结分岔点B)。Hopf分叉点A对应的速度90.1 m/s为线性临界速度,鞍结分岔点B对应的速度80.7 m/s为非线性临界速度。当速度小于非线性临界速度时,轮对对任何扰动均具有抗干扰作用,其稳态运动都能收敛于平衡位置从而保持稳定;当速度位于非线性临界速度和线性临界速度之间时,当轮对的初始扰动幅值较小(虚线以下)时,轮对系统稳态运动逐渐收敛于平衡位置而保持稳定,但当出现大幅初始扰动(虚线以上)时则逐渐趋于实线从而失稳,此时系统小激扰稳定而大激扰失稳;当速度高于线性临界速度时,系统完全失稳,任何扰动都能导致稳态运动发散。
轮对超临界Hopf分叉见图2(b),Hopf分叉点A对应的速度为84.3 m/s,为临界速度。当速度低于84.3 m/s时,轮对系统稳定,对任何扰动均具有抗干扰效应,稳态运动均收敛于平衡位置;当速度高于84.3 m/s时,轮对系统失稳,任何扰动都能导致稳态运动发散直至出现极限环。
2.2 轮对系统的随机稳定性
随机稳定性分析可采用奇异边界方法[19],这种方法的缺点是只适用于一维,对于高维问题则无能为力,但随机平均法的降维功能恰好弥补了这一缺陷,为奇异边界方法的实施奠定了基础。
对于式(11)的一维能量扩散解过程H(t),其概率为1渐近稳定性与其平稳概率密度的存在性反映系统长期行为的性态,而系统长期性态可通过边界性态间接获取。接下来将重点分析能量扩散过程H(t)在左右2个边界上的性态。
对于右边界H=∞,有|m(∞)|=∞,根据一维扩散过程边界分类[20]可知,右边界边界类型为无穷远处第二类奇异边界。对式(14)关于θ求期望,得

当H→∞时,R的低次项可忽略,H应对应R的高次项,则有,代入式(12)可得

对于左边界H=0,当H=0时,有σ2(0)=0,m(0)=0,则左边界类型属于第一类奇异边界(套点)。此时对应的漂移和扩散系数满足如下条件

根据第一类奇异边界理论[20],边界扩散指数αL、漂移指数βL以及特征标值cL分别为(下标L表示左边界)

当特征标值cL<1时,则有左边界H=0是吸引自然边界,由于右边界不受特征标值影响,这样解曲线H(t)会由于排斥效应远离左边界而逐渐趋向于左边界,说明能量逐渐稳态收敛于0,此时系统解曲线H(t)是全局稳定的。
相反,当特征标值cL>1时,左边界也是排斥自然边界,由于排斥效应解曲线H(t)会同时远离左右边界,解曲线H(t)最终会收敛于某个稳态能量处(见图3)。此时系统解曲线H(t)是随机不稳定的。

图3 轮对随机系统稳定性边界分类示意
稳态能量的具体位置对应能量稳态概率密度函数的峰值,而能量稳态概率密度函数需要通过求解系统的FPK(Fokker Planck Kolmogorov equation)方程获得,这项内容涉及随机P 分叉的研究内容,本文暂不作讨论,后续研究中会有涉及。
当cL=1时,左边界为严格自然,此时边界状态处于吸引和排斥临界状态,对应系统随机稳定性临界状态,可导出系统的随机稳定域边界。由式(18)可得

将表1中相关参数代入方程(19),可得两类轮对系统的左边界特征标值cL与激扰强度D、速度v的关系(见图4),2种情形下规律基本一致,特征标值cL与速度v、激扰强度D正相关,速度v和激扰强度D越大,cL越大。当速度v和激扰强度D逐渐增大使特征标值大于1时,系统跨越绝对稳定区域边界,出现概率意义失稳。
车辆稳定性研究的首要任务是将车辆运行速度控制在稳定安全域内,接下来将分别针对两类轮对系统,确定随机稳定域及稳定区域边界,为车辆安全性设计提供理论指导。
两类轮对系统的随机稳定性临界曲线见图5,临界曲线正好是绝对稳定区域与随机不稳定区域的分界线,曲线上方为随机不稳定域,曲线下方为绝对稳定域。车辆运行速度须控制在绝对稳定区域内,若速度跨越稳定域边界,轮对发生随机分叉,可能出现失稳,造成安全隐患。在稳定性分析时需要根据车辆参数确定系统稳定域,随机激扰的激扰强度D可以通过试验模拟,只要确定了最大可能的激扰强度Dmax,然后将车速控制在Dmax对应的绝对稳定区域内即可保证车辆的安全性。

图4 轮对随机系统左边界特征标值

图5 轮对系统随机稳定临界曲线
2.3 轮对系统的随机分叉
随机分叉与一般的确定性分叉不同,随机分叉研究的重点主要集中于随机激扰引起的非线性突变或跃迁现象。一般来说,随机分叉主要有两类:一类是随机动态分叉(Dynamical bifurcation),又叫D 分叉;另一类是随机维象分叉(Phenomenological bifurcation),也叫P 分叉。一般来说,动态分叉先于维象分叉,为了求解全局随机临界速度,本文只研究前者。
随机动态分叉主要关注系统不变测度的动态特性,比较普遍的做法是通过研究Lyapunov指数这一不变测度的动态突变或跃迁变化,实现轮对的随机动态分叉分析。因此,研究动态分叉的关键在于最大Lyapunov指数的计算。
实际上,由于随机平均法保留原轮对系统的主要非线性特性,因此随机平均后的平均Itô随机微分方程的最大Lyapunov指数可近似等价于原系统方程,则问题转化为研究平均Itô随机微分方程(11)的最大Lyapunov指数。将平均Itô 随机微分方程(11)在H=0处线性化,得

由上式可求解得

则系统的最大Lyapunov指数为

当H→0时,式(14)中关于R的高次项可忽略不计,对该式R的低次项部分关于θ求期望,可得

即R2=2H,则有

则可得轮对系统最大Lyapunov指数为

当λ<0,轮对系统概率1渐近稳定,此时系统的能量增长速率慢于能量消耗速率,系统的总能量会逐渐耗散并趋于0,系统绝对稳定。最大Lyapunov指数λ的大小对应系统总能量的耗散速度,λ越小说明能量减小的越快,系统稳定性能越好。
当λ>0,轮对系统为概率1 渐近不稳定,此时系统的能量消耗速率小于能量增长,总能量将逐渐累积,系统动能会逐渐增加,可能出现失稳及分叉现象甚至发生脱轨。
当λ=0,轮对系统处于随机稳定临界状态,λ对应的零点为系统随机动态分叉点。
轮对随机系统的最大Lyapunov指数λ这一特性有点类似于确定系统中的特征根实部,λ<0是系统概率1渐近稳定的充要条件。根据表1中的轮对参数,分别画出了不同激扰强度D下两类轮对系统的最大Lyapunov指数随速度变化图,见图6。
由图6可知,最大Lyapunov指数λ与激扰强度D、运行速度v具有正效应,当激扰强度D和运行速度v增大时,最大Lyapunov指数会逐渐增大并由负变正,此时轮对系统由概率为1稳定变为不稳定,系统发生随机动态分叉。

图6 最大Lyapounov指数随速度变化
当λ=0时,为随机动态分叉临界点,此时对应的速度为动态分叉临界速度,记为vD。
此外,分别针对两类轮对系统,对比分析奇异边界法与最大Lyapounov指数法的分析结果,两类轮对系统对比分析见图7(图中激扰强度D=0.05),对比结果显示2种方法的分析结果完美契合,动态分叉临界速度vD与随机稳定域边界对应的速度值正好相同,且两类轮对系统结论一致,侧面应证了奇异边界法和最大Lyapunov指数法的有效性。
综上所述,随机参激对轮对系统临界速度影响较大,当随机激扰强度逐渐增大时,临界速度显著减小。随机动态分叉前轮对系统动态特征为概率1意义下的随机稳定运动,此时系统绝对稳定;随机动态分叉后系统动态行为比较复杂,其具体特征需要通过P分叉进一步研究。
2.4 随机动态分叉与Hopf分叉的对比
前文通过随机动态分叉研究得到了随机动态分叉临界速度vD,但是随机动态分叉概念不够直观,为了详细说明随机动态分叉以便于理解,接下来将随机动态分叉与确定性Hopf分叉进行对比,探究随机动态分叉和传统分叉之间的联系,建立随机动态分叉和传统Hopf分叉沟通的桥梁。

图7 随机稳定性与动态分叉对比
随机动态分叉临界速度随激扰强度的变化曲线见图8。图8中vDs和vDp分别为超临界系统和亚临界随机动态分叉临界速度,vH为超临界系统Hopf分叉临界速度,vA为亚临界轮对系统鞍结分叉临界速度。从图8可以看出,当D→0时,超临界轮对系统中动态分叉点逐渐趋近于Hopf分叉点,而亚临界轮对系统中动态分叉点逐渐趋近于鞍结分叉点。当激扰强度时,随机动态分叉逐渐退化为确定性分叉。需要说明的是超临界轮对系统Hopf分叉点和亚临界轮对系统鞍结分叉点都是各自轮对系统的全局(最小)临界速度,当速度小于全局临界速度时,系统绝对稳定,也就是说随机动态分叉临界速度可定义为轮对系统的全局随机临界速度。在随机激扰下,临界速度出现向前漂移现象,且随着激扰强度增大,动态分叉临界速度显著变小。

图8 随机动态分叉临界速度随激扰强度变化曲线
在传统车辆稳定性理论中,认为车辆临界速度跟外部激扰无关,激扰只是改变了系统的初始状态,一旦激扰撤去,系统稳态解仍会呈现Hopf分叉相应特征。这一观点本身并没有问题,只是考虑问题的角度不同而已,实际上外部激扰存在时,车辆系统不能再单纯考虑车辆本身,应该将它们作为一个耦合的大系统来分析。这也打破了确定性车辆系统中的临界速度的思维定势,车辆的临界速度不再是单一的固定值,而是随激扰强度变化而改变的,这也可以从理论上解释车辆在不同线路下的失稳临界速度不同的原因。
车辆在实际运行中随机激扰无处不在,常规情况下车辆受到的随机激扰源主要是轨道不平顺激扰,但相对来说轨道不平顺激扰属于弱随机因素,一般情况下其激扰强度D较小,根据前述理论分析结果可知,系统的临界速度漂移量较小,符合实际车辆运行情况。但是当遇到大风、强震等极端激扰条件下,此时激扰强度D较大,车辆系统的临界速度会显著降低,稳定性能急剧恶化,而用Hopf分叉理论显然无法解释这一点。因此,常规运行时分析车辆稳定性时,随机激扰影响不大,但遇到大风等强激扰环境时,随机激扰的影响将不可忽视。
此外,随机动态分叉点对应的速度为系统的全局随机临界速度,最大Lyapunov指数法对随机激扰具有鲁棒性,这为新的线路失稳判定方法提供了理论依据。最大Lyapunov指数可以通过时间响应序列直接计算,凭借这一优势,该方法将可以直接应用到线路失稳判定中。
3 结论
本文运用随机平均法研究了两类轮对系统的随机稳定性以及随机动态分叉,定义了全局随机临界速度,提出了以最大Lyapunov指数法为基础的失稳判定方法,获得了以下主要结论:
(1)随机动态分叉点对应的速度为轮对系统的全局随机临界速度,超临界Hopf分叉系统中动态分叉点对应于Hopf分叉点,亚临界Hopf分叉系统中动态分叉点对应于鞍结分叉点。
(2)动态分叉前轮对系统动态特征为概率1 意义下的稳定运动,分叉后轮对系统具体特征需要通过P分叉进一步研究。
(3)随机因素对轮对系统平衡点的稳定性有决定性影响,随机激扰使轮对系统的临界速度出现向前漂移,随着激扰强度增大,临界速度漂移量显著增大。
(4)轮对系统的临界速度不再是单一的固定值,而是随激扰强度变化而改变的,这也从理论上解释了不同线路条件下失稳临界速度不相同的原因。
(5)常规运行时分析车辆稳定性时,随机激扰影响不大,但遇到大风等强激扰环境时,随机激扰的影响将不可忽视。
(6)最大Lyapunov指数法可作为线路失稳判定的新方法。
