相控阵雷达长时跟踪波束调度与波形优化策略
2020-04-16刘一鸣盛文胡冰张磊
刘一鸣,盛文,胡冰,张磊
空军预警学院 防空预警装备系,武汉 430019
在现代化的战争中,战场环境日趋多样化、复杂化和持久化。大型相控阵雷达作为预警体系中的骨干装备,其功能的充分发挥对整个预警体系的作战效能起到了至关重要的作用。而跟踪工作模式占据其大部分资源,所以利用自适应波束波形调度策略来提高多目标跟踪性能的研究是不可或缺的。
相控阵雷达多目标跟踪波束调度策略是利用对目标状态变量的估计和当前可用资源制定相应的规则,来实现在跟踪波束调度时刻做出合理决策的目的。相控阵雷达作为一种特殊的传感器,其管理策略与多传感器有很多相似之处,常见的传感器控制方法包括信息论[1-2]、协方差[3-4]和克拉美罗下界(Cramer-Rao Low Bound, CRLB)[5],很多学者将其引入相控阵雷达多目标跟踪资源管理的研究中取得了丰硕的成果。文献[6]在信息论的框架下,将跟踪前后信息熵的变化作为跟踪精度的衡量指标来控制跟踪波束的调度情况。但是该方法将每个目标的精度需求视为相同的,这与实际的作战环境是不相符的。进而,鉴于协方差控制的方法具有很强的自适应性,文献[7]提出了基于协方差偏差均值最小准则和最大协方差偏差最小准则的相控阵雷达多目标资源管理算法。文献[8]在最小化后验估计误差协方差的条件下,实现了对雷达波束、功率和波形参数的选择。但以上研究仅考虑了目标跟踪精度,而忽略了雷达资源的消耗。文献[9-10]通过当前时刻目标实际协方差与期望值的偏差和所选波形能量的加权平均为调度代价,进而选择下一时刻的工作方式和参数。文献[11-12]在检测概率和跟踪精度的约束条件下,预估了波束的驻留时间,通过定义的紧迫(调度)系数来确定下一时刻的波束指向。然而,协方差控制思想的调度性能受期望协方差矩阵和滤波算法的影响很大,考虑到CRLB是参数估计误差的理论下界,文献[13-17]针对多输入多输出雷达波束的特性,以后验CRLB为跟踪精度的评价指标,建立相应的优化模型,对波束指向、发射功率、重访时间和驻留时间等参数实现了有效管理。
以上研究仅考虑了波束调度当前的代价,然而当前调度决策会影响到雷达对目标的观测结果,继而影响到下一时刻对目标状态的估计,最终影响下一时刻的调度决策,显然这是一个序贯的时序决策过程,所以考虑当前时刻决策的长远代价可以一定程度上提高系统整体的调度性能。文献[18-21]将多传感器网络动态控制问题描述为马尔可夫决策过程(MDP),设计了相应的参数优化策略,提高了系统的性能。文献[22]利用概率密度函数对跟踪精度进行评价,采用马尔可夫决策过程对当前时刻调度的长远代价进行建模,实现对雷达资源的实时管理,但该方法并没有考虑到雷达消耗的能量。文献[23]将雷达跟踪资源管理问题建模为MDP,设计了发射功率、载频、驻留时间和采样间隔优化策略,并提出了一种改进的二元风驱动优化算法加速最优策略的求解。文献[24]类比随机控制问题,将雷达多目标跟踪目标选择问题建模为MDP,给出了相关策略,降低了资源过载时多目标跟踪误差。上述研究不断丰富了相控阵雷达跟踪波束调度的内容,但仍存在以下不足:调度策略设计过程中没能考虑到跟踪资源对不同目标跟踪精度改善程度的差异性。
针对上述文献中未能综合考虑跟踪资源对不同目标跟踪精度改善程度的差异性和决策长期性的问题,研究了相控阵雷达波束调度和波形参数优化的问题,将上述序列决策问题建模为一个离散MDP,利用有限阶段的累计资源消耗收益率来衡量当前时刻资源对目标跟踪精度改善的差异性,进而与当前时刻的实际跟踪精度相结合作为长时策略的回报函数,考虑到预测的准确性,利用预测的后验克拉美罗下界(Posterior Cramer-Rao Low Bound, PCRLB)来衡量预测精度,而实际精度仍采用协方差来表征;同时,提出了一种并行混合遗传粒子群算法来求解最优策略,最后在多目标跟踪场景下,将所提调度策略与其他已有方法进行对比,验证了有效性和优越性。
1 基于MDP的跟踪波束波形调度模型
相控阵雷达多目标跟踪波束波形调度问题可描述为:如何根据当前时刻的滤波结果确定下一时刻跟踪波束指向及跟踪波形参数。为提高系统长期跟踪性能,可将其建模为一个序列决策问题,而序列决策模型要求决策者不仅要考虑决策的即时效应,还要考虑为将来决策创造机会,则tk时刻的具体决策过程如图1所示。同时多目标跟踪滤波过程具有明显的马尔可夫性,故将该问题建模为MDP,基于MDP框架,本文的具体模型要素如下。

图1 tk时刻长期决策过程示意图Fig.1 Schematic diagram of long-term decision-making process at tk time
1.1 调度动作
定义tk时刻的调度动作向量ak=[akp,akw]T,其中akp为tk时刻雷达的波束指向,akw=[akτ,akT]为tk时刻雷达跟踪波形参数向量,akτ为驻留时间,akT为跟踪采样间隔。
1.2 系统状态与状态转移
系统状态即跟踪目标运动状态,定义tk时刻的系统状态Xk=[xk,yk,vxk,vyk]T,其中xk、yk、vxk和vyk分别表示目标在x和y方向的位置和速度。则系统的状态及状态转移可表示为
Xk+1=FkXk+ωk
(1)
式中:Fk为状态转移矩阵;ωk为零均值高斯噪声,其协方差矩阵为Qk。
1.3 系统观测及观测矩阵
定义tk时刻的系统观测Zk=[rk,θk]T,其中rk为目标距离,θk为目标方位角。则系统的观测方程可表示为
Zk+1=H(Xk+1)+νk
(2)
式中:H(·)为雷达的非线性观测函数;νk为零均值高斯量测噪声,其协方差矩阵为Rk。
1.4 回报函数
相控阵雷达长期调度的关键是对系统未来状态的准确预测,而PCRLB给出了目标状态估计误差的理论下界,故将其作为预测精度的衡量指标。PCRLB定义为Fisher信息矩阵(FIM)的逆矩阵[25],即
(3)

针对本文问题,文献[26]提出了FIM的递推求解方法,即
(4)
式中:Gk+1=∂Xk+1H(Xk+1)为观测矩阵的雅可比矩阵。
相控阵雷达消耗的资源可分为时间资源和能量资源,其中能量资源主要为发射功率和脉冲宽度,时间资源主要为驻留时间和采样间隔。本文不考虑辐射控制的问题,假定发射功率和占空比值为最大值,故仅考虑时间资源的消耗,所以雷达跟踪消耗的资源Ek由驻留时间dk和采样间隔Tk来表征,即
Ek=dk/Tk
(5)
目标跟踪精度仅考虑位置估计误差,为了便于目标后验克拉美罗下界的量化以及后续的计算,故从Ck中提取位置分量估计误差的下界,并取其迹和Frobenius范数(F范数)作为其量化值Bk,用ΔAk描述Bk的变化率,即
(6)
式中:blkdiag(·)为生成指定对角线元素的矩阵;Im为单位矩阵;⊗代表Kronecker运算。
为了提高系统长期调度的性能,就要充分考虑调度时刻目标消耗相应资源给系统带来回报的差异性,借鉴效益理论中效费比这一核心概念来描述预测资源消耗回报率,可以实现对波束调度过程的精确控制,进而提高管理过程效益。然而,相控阵雷达系统中资源种类繁多,如波形资源、设备运算资源和存储资源等,需对调度过程中资源概念予以界定。跟踪波束波形调度决策问题只关心波形能量的调度情况,故上述“资源”具体指发射波形资源,对应的“效费比”是波束调度效费比ηk,定义为预测精度变化率与发射波形资源消耗的比值,即
ηk=ΔAk/Ek
(7)
同时,当跟踪目标的跟踪精度超过精度门限时,应及时调度这些目标,故需要将决策时刻各目标的实际跟踪误差考虑到回报函数中来。首先,目标跟踪的误差协方差矩阵不能衡量大小,需要取其某种意义下的范数值来反映其误差水平;同时,由于协方差矩阵中对角线上元素可以很好地体现目标位置估计误差的水平,故取误差协方差矩阵的F范数来表征目标实际误差协方差矩阵的大小,当某个目标当前实际误差超过门限时,但其波束调度效费比很小,这会使得这些目标不能及时被调度,所以定义一步回报函数r(Xk,ak)为
r(Xk,ak)=
(8)
式中:F[P(akp)]表示tk时刻目标akp实际跟踪协方差矩阵P(akp)的F范数;Pthr为设定的跟踪精度门限,记优势系数κk=maxηk为tk时刻所有策略中资源效费比的最大值,目的是让跟踪误差超过门限的目标波束调度效费比绝对占优。
定义R(Xk,ak,ak+1,…,ak+n,n)为在系统状态为Xk时采取系列动作Ak:k+n=[ak,ak+1,…,ak+n]时n步预测的回报函数,即
(9)
式中:ατ为τ+1步预测的折扣因子,用于表示各步预测的重要程度。
2 问题模型建立
2.1 目标跟踪滤波算法
目标跟踪算法主要用于对目标状态预测和观测进行滤波,使其更接近目标实际运动情况。考虑到系统为非线性高斯,常用的算法有扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)和粒子滤波(PF),EKF计算量较小,但仅适合于弱非线性高斯系统;PF适用于任何非线性高斯系统,但其本质上属于蒙特卡罗方法,计算量大;UKF计算量适中,且适合于非线性高斯系统。本文的状态方程仍为线性高斯,故可采用简化无迹卡尔曼滤波(SUKF)算法,其具体步骤为

(10)

(11)
式中:λ=α2(L+b)-L为尺度参数,用来降低总的预测误差,α控制了采样点的分布状态,通常设为一个较小的正数(1×10-4≤α<1),b为待选参数,通常取0或3-L;β为状态分布参数,对于状态变量为高斯分布,通常取β=0为最优。

(12)
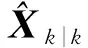
(13)
2.2 相控阵雷达长时调度策略
在调度过程中寻求的最优策略,不仅是要最大化回报函数,还要满足检测和跟踪的基本要求,所以本文的长时调度策略优化模型可描述为
(14)

2.3 策略实现流程
上述调度策略下的资源管理框架描述如图2所示,资源管理流程实际上是一个最优控制的过程,调度过程主要由波束调度及波形参数优化和最优策略执行2个模块构成,具体步骤为

图2 长时调度策略最优控制流程Fig.2 Optimal control flow of long-term scheduling strategy


步骤3tk时刻波束调度及波形参数优化(为简化表示,以下推导忽略目标编号)。

(15)
式中:SNRref、τref和rref分别为参考信噪比、驻留时间和目标跟踪距离。
假设目标的起伏模型为SwerlingⅢ型,虚警概率为Pf,故可得预测的检测概率为
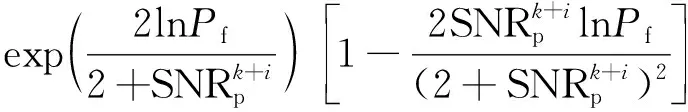
(16)

(17)
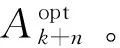
2.4 混合优化算法
本文马尔可夫决策问题的最优决策序列可转化为动态规划算法结构进行求解,但是随着预测步数的增加,寻求最优策略的效率就会下降,故引入智能优化算法加快寻优速度。常用的遗传算法(Genetic Algorithm, GA)全局搜索能力强,粒子群优化(Particle Swarm Optimization, PSO)算法收敛速度快,其混合算法在雷达参数优化[27-29]方面得到了成功运用,但是上述混合算法均是将其中某一算法的核心思想引入到另一种算法中,本文提出了一种并行混合GAPSO算法,将2种算法更新的种群对比选优组成新的种群,其算法流程如图3所示,流程中关键步骤说明如下:
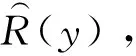
(18)
式中:cmin为常数,取R(y)的最小值。
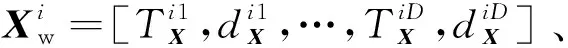
(19)


图3 并行混合GAPSO算法实现流程图Fig.3 Flow chart of parallel hybrid GAPSO algorithm implementation
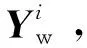
1) 选择算子。选择又称为复制,是在群体中选择生命力强的个体产生新群体的过程,利用比例选择方法,则个体i被选则概率Pi为
(20)
通过上述方式会破坏适应度较高的优良个体,使问题收敛速度慢甚至陷入局部最优,故引入最优保存策略来保护优秀个体,其基本思想概括为:当前种群中适应度最高的个体不参与进化,而是用它替换掉本代种群中经过杂交、变异等遗传后所产生的适应度最低的个体。
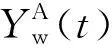
(21)
式中:α为一个参数,α∈(0,1)。同时,交叉操作的执行与否由交叉概率Pc决定。
3) 变异算子。变异算子是个体间染色体等位基因替换的过程,为了增加种群的多样性,本文采用均匀变异的方式,其操作过程描述为:依次指定个体中每个基因座为变异点,对每个变异点,以变异概率Pm从对应基因的取值范围内取一随机数代替原来的基因值。
3 仿真实验
由于目标的机动性和目标位置预测的局限性,过分的长期预测可能会带来较大的预测误差,从而影响目标的跟踪精度。因此,为分析长时调度策略中决策步长对目标跟踪精度的影响,选取不同的预测步长n进行实验。为了验证上述策略中回报函数和长时调度方式2点创新性工作的有效性和优越性,在同一仿真场景下,选取相应短时调度策略和常规的波束波形联合调度策略[9-10]2种方法进行对比验证。
3.1 对比方法介绍
方法1 该方法在上述调度策略的基础上,采用一步预测方式对目标进行跟踪。
方法2[9-10]该方法中的调度策略的目标函数选为预测跟踪精度与波形能量的归一化加权平均值。
3.2 仿真场景


图4 责任区内跟踪目标运动轨迹Fig.4 Tracking target motion trajectory in area of responsibility
3.3 仿真结果
在上述多目标场景中,为了更全面地反映目标的跟踪情况,将均方根误差(Root Mean Square Error,RMSE)作为跟踪质量的评价指标,信号驻留时间和采样间隔时间作为资源消耗的评价指标。图5给出了不同方法下各目标在调度过程中的RMSE,可以看出,长时调度方法在调度过程中的跟踪精度普遍高于方法1和2,同时,方法1的跟踪精度要高于方法2;图6给出了不同方法下目标在调度过程中的平均资源消耗情况,可以看出,长时调度方法在保持适中的采样间隔时间水平时能够利用更多的驻留时间来跟踪目标,然而方法2相对方法1具有更高的采样间隔时间水平并利用更多的驻留时间来跟踪目标。综上分析可得,长时调度策略通过回报函数可以选择各决策时刻的最优跟踪目标,进而实现对采样间隔时间和驻留时间的最优控制,通过预测步长的增加,来提高整体的调度性能。
为了精确刻画长时调度策略的优越性,表1给出了各方法性能指标和决策时长的统计结果,实验环境为MATLAB2016a,实验的平台为Windows10 64位操作系统,计算机配置为Intel Corei5-8250U CPU,主频1.6 GHz,显示适配器NVIDIAGeForce MX150,可得当预测步长n=5时,跟踪精度相对方法1提高11.17%,方法1相对方法2提高1.69%。
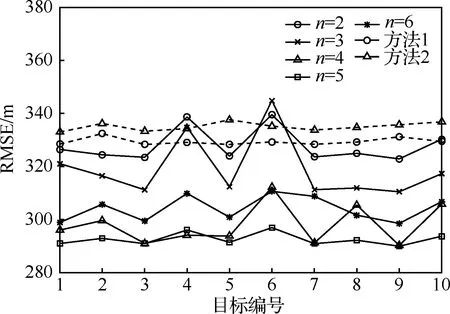
图5 不同方法下各目标RMSEFig.5 RMSE of each target under different methods
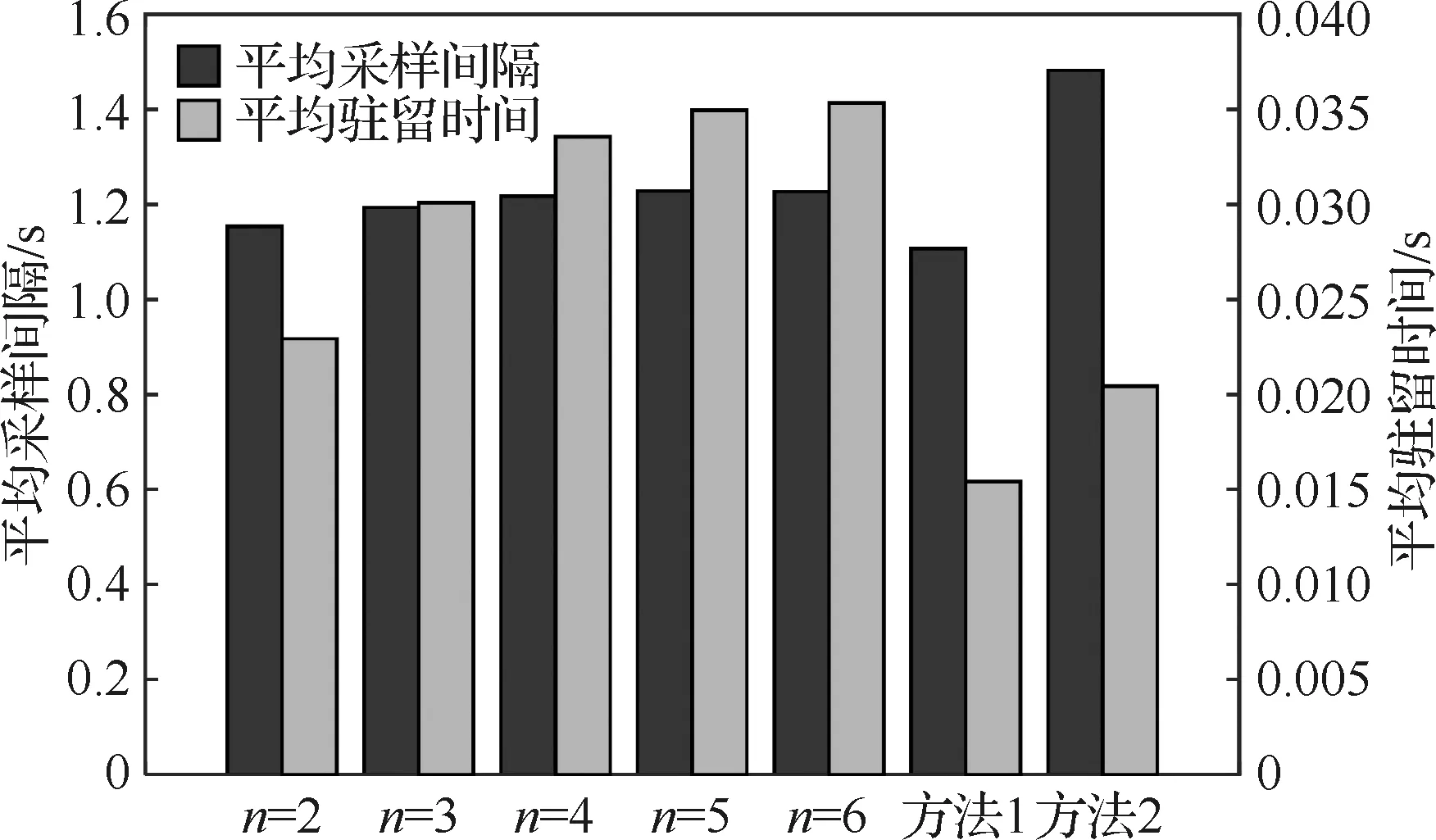
图6 不同方法下调度过程平均消耗资源Fig.6 Average consumption of resources in scheduling process under different methods
表1 长时调度策略下跟踪性能指标和决策时长统计值
Table 1 Tracking performance indicators and decision duration statistics under long-term scheduling strategy

方法均方误差/m驻留时间/s采样间隔/s决策时长/s预测步长n=2327.820.022931.15385.6698n=3319.170.030081.19357.4832n=4305.800.033551.21729.5013n=5292.600.034961.228012.507n=6306.740.035341.226515.445方法1329.410.015421.10723.9864方法2335.080.020441.48231.1809

图7 RMSE和决策时长随预测步长的变化曲线Fig.7 RMSE and decision duration as a function of predicted step size
为了更好地分析长时调度策略整体调度性能和预测步长的关系,取步长n=2,3,4,5,6情况时进行分析,图6和表1给出了调度过程中时间资源消耗随预测步长的变化情况,可以看出,随着预测步长的增加,驻留时间和采样间隔时间都有所增加;图7给出了调度过程中RMSE和决策时长与预测步长的关系,可以看出,随着预测步长的增加,决策时长增加且增长速度越来越快,RMSE先减小再增加,即跟踪精度先增加后减小,在预测步长n=5时获得最优跟踪精度,这是因为长期预测的优势是建立在目标状态预测准确的基础上,而跟踪目标存在机动特性,从而大大降低了预测的准确性,最终导致决策的偏差。综上所述,针对不同的作战场景,在一定的预测步长范围内,长期调度策略要优于短期调度策略,最优步长需要在调度过程中寻找并设置。同时,当最优预测步长所需较长的决策时长时,决策者需要在跟踪性能和决策实时性之间进行合理地权衡。
同时,为了进一步体现长时调度策略的优越性,选取在各方法中跟踪调度情况均较好的目标1进行分析,考虑到上述情况分析的结果,选取n=5、方法1和方法2这3种方法进行分析,结果如图8所示,可以看出长时调度策略在目标跟踪误差超过门限后能及时对其进行调度,很大程度上避免了目标失跟,然而其他2种方法没有这种控制效果;同时随着时间的推移,目标跟踪精度的变化趋于稳定且能保持在较低的跟踪误差水平。
为了更好地展现长时调度方法在调度过程中对目标跟踪精度的控制情况,选取预测步长n=5时对波束照射情况进行分析,结果如图9所示,可以看出,在整个调度过程中雷达对大部分目标的照射次数相当,虽然各目标在不同时刻的回报函数值存在差异,但各目标本身的运动特性相似,所以回报函数在各决策时刻所反映的目标间的差异体现在目标的状态,而并不是目标本身的属性。
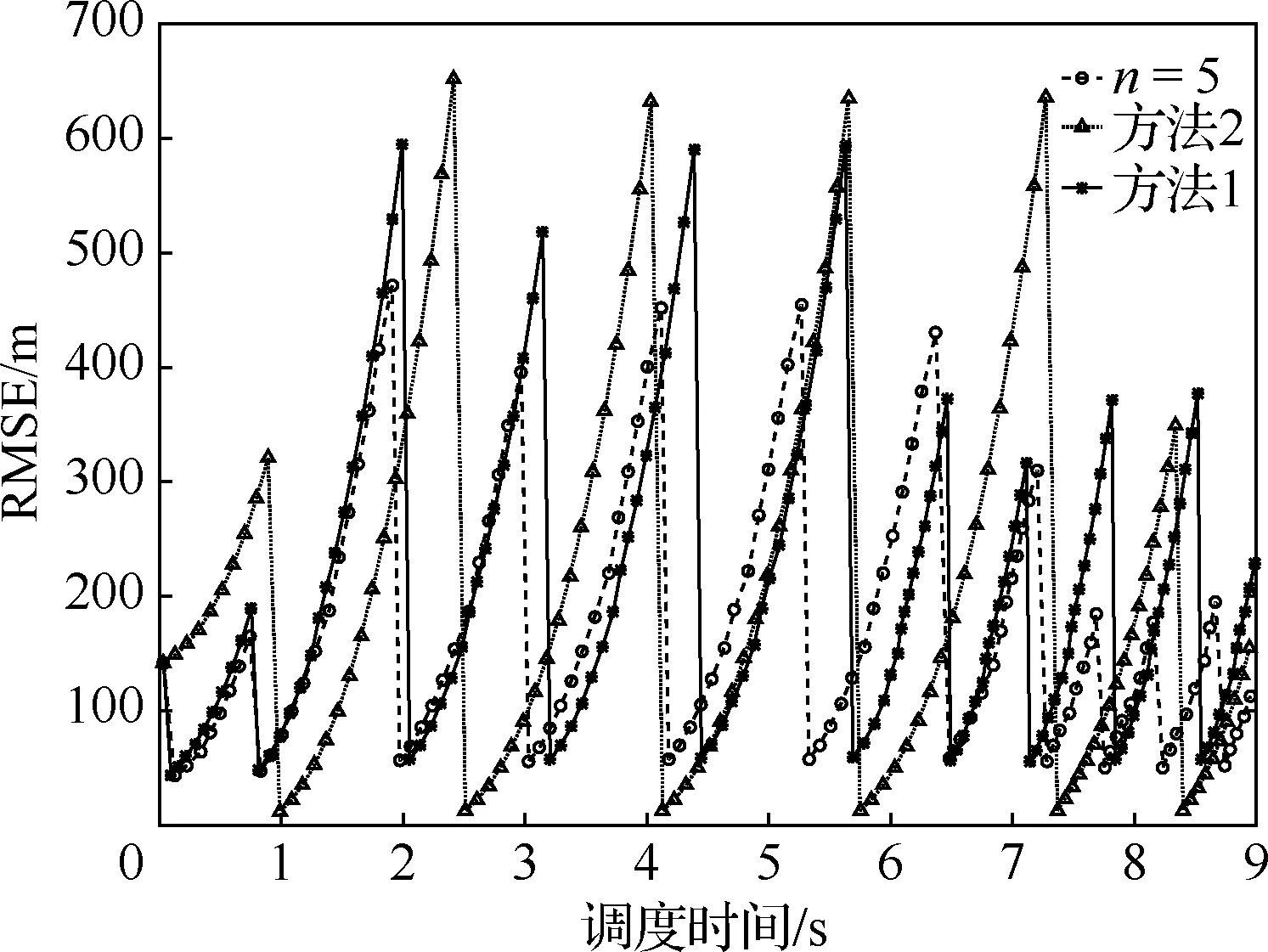
图8 3种方法下目标1调度过程RMSE 变化情况Fig.8 Changes in RMSE of target 1 scheduling process under three methods
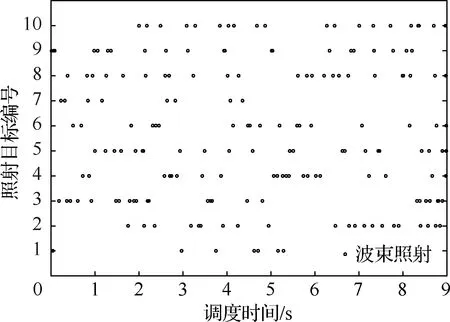
图9 预测步长n=5时调度过程波束照射情况Fig.9 Scheduling process beam illumination when predicting step size n=5
4 结 论
借鉴了马尔可夫决策过程的理论框架,将波束波形调度问题建模为序列决策问题,提出了基于马尔可夫决策过程的波束波形联合长时调度策略,仿真分析表明,所提出的调度策略:
1) 可以在各决策时刻选取最为合适的目标进行调度,在保证跟踪精度的同时,适当增大了跟踪驻留时间和采样间隔时间,提高了时间资源利用率。
2) 在调度过程中,能够及时对跟踪精度超门限目标进行调度,有效提高了跟踪目标容量,降低了失跟率。
3) 存在最优步长,同时,调度性能的提高是以牺牲决策实时性为代价,实际运用过程中决策者需要在性能和实时性之间进行权衡,进而选取合适的预测步长。
4) 为解决波束波形联合调度问题提供了一个很好的理论框架,具有良好地拓展性,可解决多目标决策问题。
