三层三级民机修理级别经济性分析模型的改进

贾宝惠，邓婉怡，王毅强

中国民航大学 航空工程学院， 天津 300300

修理级别分析(Level of Repair Analysis，LORA)综合考虑维修成本、各级别维修能力、维修操作需求等因素，在部附件发生故障时确定可行的、效费比最佳的修理级别或做出报废决策。修理级别分析的结果将作为维修任务分析的主要依据，帮助识别和量化所需的维修保障资源，进而对系统设计、维修计划和集成产品支持要素资源决策等产生影响。在飞机的设计、研制阶段尽早实施LORA，可以使各级别维修需求与现有保障资源保持平衡，以达到降低维修成本的目的[1]。民用飞机的部附件产品通常具备多个层次(Multi-indenture)，维修场所也被划分为多个级别(Multi-echelon)[2]。多层多级模式下的修理级别经济性研究对于民机复杂保障体系下提高维修效能具有重要的意义。

LORA作为一种降低全寿命周期成本的重要途径，在近20年内一直受到国内外研究者的极大关注。20世纪70年代，LORA的概念首次出现在美国国防部的IRLA(Item Repair Level Analysis)项目中[1]。1993年美国军方在军用标准MIL-STD-1390D中给出LORA的基本要求和工作描述[3]，于2014年采用工业标准SAE AS1390，规定了实施修理级别分析活动的标准化方法[4]。2015年美国国防部颁布了文件MIL-HDBK-1390，并在其中讨论了LORA敏感性和决策分析等内容[5]。中国1997年颁布了国军标GJB2961-97，对航空装备和军事设施的保障工作进行指导[6]。

上述标准均未给出详细的经济性分析模型,如何建立LORA模型一直是行业研究的热点和难点。国外相关研究起步较早，较有影响力的是Barros、Saranga和Basten分别提出的3种模型。Barros在1998年首次提出LORA-BR IP模型[7]，该模型假设报废的可变成本在每级修理网络都相等，且固定成本由一个维修层级承担。Saranga和Kumar放宽了LORA-BR模型对固定成本计算的约束，提出由每个部件独立承担成本的SDK模型[8]。Basten等综合考虑前人研究成果建立了允许设备共享情况下的LORA模型[9]，增加了模型的灵活性，该模型通过删除大部分变量的完整性约束，大大减少了计算时间。以上3种模型都是建立在故障率恒定假设的基础上，Rawat和Lad首次提出了基于时变故障率的修理级别分析规划方法[10]，并考虑预防性维修和维护质量对LORA的影响[11]。国内的LORA研究以非经济性分析方法为主[12]，经济性分析研究专注于探索更高效的求解算法：吴昊等采用免疫粒子群算法求解SDK模型[13]；贾宝惠等采用遗传禁忌搜索算法[14]和AHP-SPA方法研究民机LORA问题[15]；薛陶等采用迭代-贪婪启发式算法求解LORA与备件的联合优化问题[16]。

当前关于LORA的研究，主要以降低维修成本、提高设备保障率为目标，忽略了维修活动中由于误拆、二次维修等人为因素造成的不可避免的维修成本[17]。同时，指标参数模型不明确，也降低了模型在工程实际中的适用性。此外，Baston等指出，现有LORA模型对于父单元和子单元决策关系处理模糊[18]，报废和移位维修时存在父单元、子单元重复累加，无法真实地反应维修总成本，会影响到LORA决策的正确性。本文旨在弥补上述不足，结合民机保障体系特点，建立适用于多故障模式的多层多级LORA模型，给出考虑人为因素成本的具体计算方法，同时解决现有LORA模型中父单元和子单元报废、移动2种决策成本重复累加的问题。通过仿真案例分析，表明了本文所提出模型的有效性和实用性。

1 民机维修策略

就修理级别分析而言，民机保障体系相较于军机保障体系在维修级别和维修决策方面更加灵活多变。以下从产品结构层次、维修级别和维修决策3方面进行详细对比。

1) 对于产品结构层次，民机和军机做法一致，可划分为外场可更换件(Line Replaceable Unit，LRU)、内场可更换件(Shop Replaceable Unit，SRU)、内场可更换件子件(Sub-Shop Replaceable Unit，SSRU)等多个层级。

2) 对于维修级别，军机维修级别分为3级：基层级(外场级)、中继级(野战级)和基地级(后方级)[6]。而民机维修级别目前尚无明确标准，各航空公司依据自身实际情况来设置维修级别，部分小型航空公司采用两级维修体制，部分大型航空公司采用三级维修体制。

3) 对于维修决策，军机维修决策包括外场维修、野战级维修、后方级维修和报废4种类型[6]。而民机维修决策目前尚无明确规定，在实际维修中，排除商业竞争、维修权限和维修能力限制等非经济性因素后，故障件可根据经济性分析模型在所有可行的维修级别中选择更换、修理、移动或报废，以达到节约维修成本的目的。民机在维修决策上较军机更加灵活。

民用飞机维修策略按时间可分为计划维修和事后维修，按空间可分为原位维修和离位维修，按维修保障能力的不同又可分为航线维修、车间维修和基地维修，详细分类如表1所列。

其中，航线的维修活动包括飞行航前航后检查、排故、LRU的更换、一般的计划性维修及其他外场勤务等；车间的维修活动包括部附件修理、中度的结构修理和改装、复杂的计划性维修等；基地的维修活动包括部附件的大修、复杂的结构修理和改装等。航线与车间的维修内容可在基地执行，对同一项维修任务在不同修理级别执行的维修成本及维修效果也不同，且维修对象的结构体系复杂，如航电设备的维修包括整机级、板卡级和芯片级。因此，根据民机保障体系的特点建立适用的LORA经济模型是非常必要的。

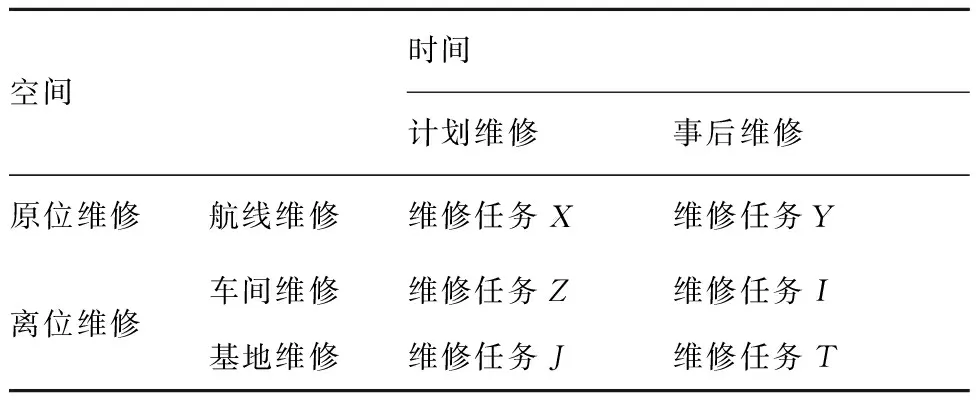
表1 民用飞机的维修策略分类

目前修理级别分析相关文献所建模型的维修模式多为两层两级或两层三级，而本文在第2节所建立的经济性分析模型为三层三级。该模型可直接处理两层三级问题，如果将三级中的某一级决策置零，也可用于求解两层两级问题，本文所建模型具有更强的适用性。

2 LORA经济性模型

修理级别经济性分析是在排除非经济性因素限制(例如维修能力、维修权限、商业竞争等)后，以节省维修成本为目的而进行的决策行为。在本文所建模型中，若不存在非经济因素限制和决策层级约束，LRU可在航线选择移动或报废，在车间选择维修、移动或报废，在基地选择维修或报废；对于SRU和SSRU，只要能最大限度地节约成本，可在内场的任何级别选择任何决策。

2.1 基本假设与符号

基于民机保障体系的特点，进行如下假设：

1) LORA待分析项的结构分为3层：LRU、SRU及SSRU，通过有序数组(i,j,k)表示待分析项层次结构间的从属关系。

2) 维修级别e分为3级：航线(e=1)、车间(e=2)、基地(e=3)。

3) 修理级别决策c包括3种选项：修理(c=r)、移动(c=m)、报废(c=d)。

4) 分析过程按照航线、车间、基地的顺序逐级进行故障判别及决策制定，直至分析完成。

5) 故障件的维修仅能从维修能力较低的级别移向高的级别。

6) 部附件的故障可能出现多种模式，例如，飞机燃油系统的交流/直流泵故障主要有电压高、油泵反转、油泵油尽、油泵转子脱落4种模式，其油位传感器故障主要有开路故障、短路故障、冲击故障、漂移故障、偏置故障5种模式，相应的维修方式也包括换件维修和不换件维修，且不同故障模式下换件维修成本差异较大[19]。

7) 不同LRU中包含同一种子单元的情况下，可根据维修选择不同的维修级别及决策。

8) 系统结构、维修级别、维修决策三者之间进行LORA匹配时存在如下限制：航线仅能决策LRU报废或移动到车间维修；车间可以在修理、移动和报废中选择一种作为决策；基地仅能决策报废或修理.详细的约束关系如图1所示。

模型的其他符号定义如下：

1)λ(i,j,k)为待分析项(i,j,k)每年的故障率。

2) VCc,e(i,j,k)为(i,j,k)在e级选择决策c产生的可变成本。

3) FCc,e,Gg(i,j,k)为通用设备集合Gg中的待分析项(i,j,k)在e级选择决策c产生的固定成本，即每年的折旧成本。

图1 修理级别分析决策匹配约束关系Fig.1 Relationship of decision matching constraints of LORA

2.2 民用飞机LORA模型

2.2.1 目标函数

(1)

式中：θ1为可变成本；θ2为固定成本。

LORA模型使用的3种决策变量的取值规则为

2.2.2 约束条件

LORA模型的本质仅对不同层级结构产生约束，同级结构间决策互不影响。因此，可以把待分析项分解成若干由(i,0,0)、(i,j,0)、(i,j,k)3层结构构成的基本单元进行分析，逐个判断决策是否违反约束。

根据民机保障体系的特点，本文LORA模型约束条件如下：

1) 维修能力的限制

(2)

(3)

(4)

约束(2)确保在航线时只对LRU选择移动或报废2种决策；约束(3)表示在车间只能选择修理、报废或移级维修三者中的一种；约束(4)表示在基地所有待分析项只能选择修理或报废。

2) 结构层次间父子单元嵌套行为的约束

(5)

(6)

约束(5)表示若父单元报废或移动，则需要对其子单元进行跟随行为标记；约束(6)表示若父单元选择移动或报废，则子单元需在同级跟随父单元行为做出相同决策。

3) 维修资源约束

(7)

约束(7)表示对每一项LORA决策都要考虑相关的设备资源限制。

4) 维修级别间的决策行为约束

(8)

(9)

约束(8)保证待分析项从低级别维修点移动到高级别维修点时，必须要在高级别维修点选择一项决策；约束(9)保证待分析项如果在低级别维修点选择维修或报废决策，则不会在高级别维修点选择任何决策。

2.3 维修成本的计算

在民机维修成本构成中，一部分费用随LORA决策的选取和设备故障率而变化，称为可变成本；另一部分费用为一次性投入的成本，与故障率无关，称为固定成本。本文所构建的LORA成本模型考虑了人为因素成本和设备维护费用成本，较现有LORA中的成本分类更为精细，更加符合民机维修的实际情况。

2.3.1 可变成本

民机维修可变成本构成如表2所示。文献[6]给出了Cl、Cm、Ct的计算方式，本文对Csph、Chf、Cd的计算进行讨论。

表2 民用飞机维修可变成本类型及其构成

1) 备件持有成本Csph

计算备件持有成本时需要确定备件库存数量，不仅要参考设备故障率，还应考虑保障率和周转时间等因素[11]。车间和基地的备件持有成本相对稳定，在模型中不作讨论。文献采用泊松分布来估计航线备件数，引入保障因子SL描述航线的保障能力，反映航线备件不缺件的置信度。由泊松过程,航线备件不缺件的概率为

PSL,Q(i,j,k)=

(10)

式中：τ为时间周期；Q(i,j,k)为零部件(i,j,k)的推荐备件数；PSL,Q(i,j,k)为在给定SL下(i,j,k)在某级恰有Q(i,j,k)个备件的泊松累积概率；λ((i,j,k),y)为第y年(i,j,k)的故障率，服从指数分布。

令保障因子PSL,Q(i,j,k)≥SL，即可求得在目标保障率SL下(i,j,k)在航线上推荐的最少备件量。备件持有成本为

(11)

式中：Cspup(i,j,k)为备件单价。

2) 人因成本Chf

在航线上维修时由于时间紧迫容易造成误判，据统计航电系统的无故障发现率(No Fault Found，NFF)约为30%，平均每架飞机的NFF事件损失超过10万美元[20]。此外，由于维修人员技术能力欠缺及隐蔽故障等原因，造成二次维修的情况也时有发生。因此，在LORA模型中应该将人为因素导致的成本偏差考虑在内。人因成本计算方法为

Chf=Cdcbm+Csm=

λ×[α×(Ct,1+Cssp)+β×RC]

(12)

式中：λ为故障率；α为航线误拆率；β为部附件需要二次维修的概率；RC为修理成本；Ct,1为e=1时的运输成本。

3) 停机成本Cd

停机成本Cd中的Cnmd属于与决策无关的必然成本，在模型中不予考虑。由于航线备件低于推荐数量而造成停机成本为

Cd=(1-PSL,Q(ijk))×(Ct-d-l+Cspd×Td-l)

(13)

式中：Td-l为车间到航线的备件周转延误时间；Cspd为单位时间内的航线停机成本；Ct-d-l为车间到航线的运输成本。

最终得到可变成本为

VC=Csph+Cd+Chf+Cm+Cl+Ct

(14)

2.3.2 固定成本

民机维修固定成本构成如表3所示。

表3 民用飞机维修的固定成本类型及其构成

LORA固定成本中的测试设备成本和维修设备成本是指设备每年的折旧成本。在计算固定成本时还需要考虑如下因素：

1) 固定成本不应按设备的使用率进行均摊。频繁使用的部件会因分摊费用过高而得到报废的决策，进一步导致同组共享设备集中的部件因分摊成本偏高而报废，最终得到错误的结果。

2) 需要考虑设备自身的维护费用。虽然不考虑设备自身的维护费用也能得到修理决策，但是该决策用到的其他各类设备的维护费可能远大于选择报废产生的费用，导致决策有选择报废的倾向。

3) 忽略固定成本中所包含的厂房建设成本、维修场所空间成本、人员工作空间成本等与LORA决策无关的部分。

固定成本的计算方法为

Ctmm+Cpte

(15)

3 模型求解

Kennedy和Eberhart于1997年在经典粒子群算法的基础上提出二进制粒子群(BPSO)算法[21]，该算法受到鸟群觅食行为的启发，种群中每个粒子在迭代过程中根据自身历史最优位置和种群历史最优位置来动态调整自己移动的速度和方向，最终收敛到原问题的最优解。BPSO算法因具有简单易行、效果良好等特点而被广泛应用于求解0-1规划问题[22]。本文采用BPSO求解LORA模型的流程图如图2所示。

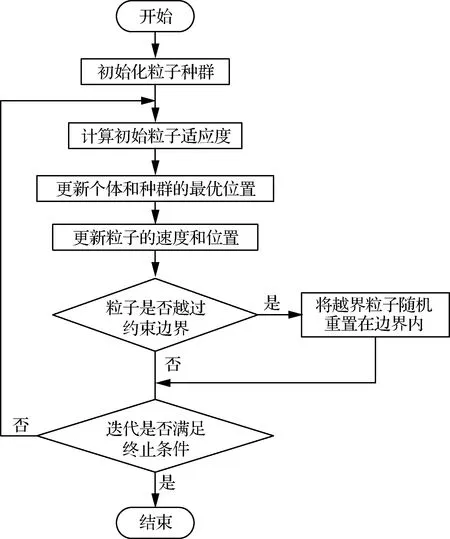
图2 BPSO算法流程图Fig.2 Flow chart of BPSO algorithm

BPSO算法的速度更新公式为

(16)

位置更新公式为

(17)

式中：T(v)为将速度值映射为概率值的传递函数。

由于待分析项嵌套结构的复杂性，导致约束条件在编程时难于实现。另一方面，粒子初始位置的设定和传递函数的选择对迭代能否顺利进行也有较大影响。目前已有文献中几乎没有给出相关的技术细节描述，基于本文研究工作给出编程求解中的4个关键步骤。

1) 复杂结构分解为简单模块

待分析项的结构特征在数学上用结构矩阵来描述，而不同系统的结构组成可能千差万别。在编程求解较大规模问题时，直接在结构矩阵上判断某决策是否满足所有约束条件存在极大困难。LORA模型中同级结构间决策互不影响，本文采取化整为零的思想，将待分析项分拆成多个由{(i,0,0),(i,j,0),(i,j,k)}三元素组成的简单模块，这样的简单模块结构固定、易于处理，在此基础上来统计所选决策违反约束的程度。例如某待分析项的结构为{(1,0,0),(1,1,0),(1,1,1),(1,1,2),(1,2,0),(1,2,1)}，可拆为以下3个简单模块:

① {(1,0,0),(1,1,0),(1,1,1)}

② {(1,0,0),(1,1,0),(1,1,2)}

③ {(1,0,0),(1,2,0),(1,2,1)}

对所有简单模块对应决策逐个统计违反约束程度，累加作为决策在整体上违反约束的程度；若所有简单模块的决策均满足约束条件，则所选决策在整体上也满足约束，模型的可行决策必须满足全部约束条件。

2) 建立惩罚函数

采用BPSO求解LORA模型时，需要将原问题转化为无约束优化问题。本文使用混合惩罚函数法[23]建立的惩罚函数为

minF(N,M,N*,t)=f(N,M,N*)+

(18)

3) 边界条件的选择

程序在迭代过程中，粒子在高维空间中动态调整自身位置以寻找全局最优解，一旦粒子越过由约束条件形成的复杂边界就很难再返回可行域。如果较多的粒子都处于边界外，迭代将无法正常进行。本文详细分析了三层三级模型对应的全部14种基本决策类型，通过分层选择决策的办法将越界粒子随机重置到可行域中，且保证每种决策被选到的概率相等。这样做的优点在于，一方面让越界粒子返回可行域继续参与优化，另一方面，给粒子以等概率抽样方式赋予的新决策有利于引导算法寻找全局最优解。

下面给出等概率生成决策的详细分析。在三层三级修理级别中，对于任意原件的决策都可以用x0到x6共7个0-1变量来描述，xi=0表示不选择该决策，xi=1表示选择该决策(i=0,1,…,5,6)，如表4所示。

表4 决策变量及其含义Table 4 Decision variables and their implications

为了方便描述所有决策类型，采用简洁的方式来记录决策结果。7个有序的0-1变量可用一个唯一的二进制数对应，例如用0110000表示的决策为：从航线移动至车间进行维修。而0110000又可以与十进制数25+24唯一对应，因此，可以用25+24这样的记号来记录决策。按照(i,0,0)、(i,j,0)、(i,j,k)的顺序从左至右依次写出14种基本决策类型，如表5所示。

表5中的每一行都代表一种决策类型，以第一行26→26→26为例，其含义为(i,0,0)、(i,j,0)和(i,j,k)同时在航线选择报废。

从表5中可以看出，每层决策仅有5种独立类型：{26,25+24,25+23,25+22+21,25+22+20}，随机生成的决策应为表格中14种决策的等概率抽样。每层中5种决策被抽中的概率不仅与其在表格中出现的频率有关，还受父单元决策的影响。决策被选中的概率可由以下条件概率进行计算。

表5 基本决策类型Table 5 Basic decision type

(19)

式中：e=1,2,3；z=1,2,3,4,5；ce,z为第e层中第z类决策；F(ce,z)为选择决策ce,z所对应父决策；m(ce,z)为具有相同父决策的ce,z在表中出现的次数；m(F(c1,z))=14。

随机生成决策时按照先父单元后子单元的顺序逐层进行，在父单元决策确定后由式(19)计算子单元选取某一决策的概率，然后按相应概率生成决策。

4) 传递函数的选择

传递函数将速度值映射到概率值，其形式对克服BPSO陷入局部最优解起着关键作用。在选择传递函数时应该遵循以下原则：

① 传递函数的值域为[0,1]。

② 粒子速度绝对值较大(小)时，传递函数应该为其改变位置提供较大(小)概率。

③ 传递函数的返回值应该随着速度的增加(减小)而增加(减小)。

文献[24]列举了8种适用于BPSO的传递函数，具体的数学形式如表6所示。

表6 V型和S型传递函数Table 6 S-shaped versus V-shaped transfer functions

表6中的传递函数按形状可分为S型和V型两大类，其图像分别如图3和图4所示。

图3 S型传递函数的图像Fig.3 Graph of the S-shaped transfer function

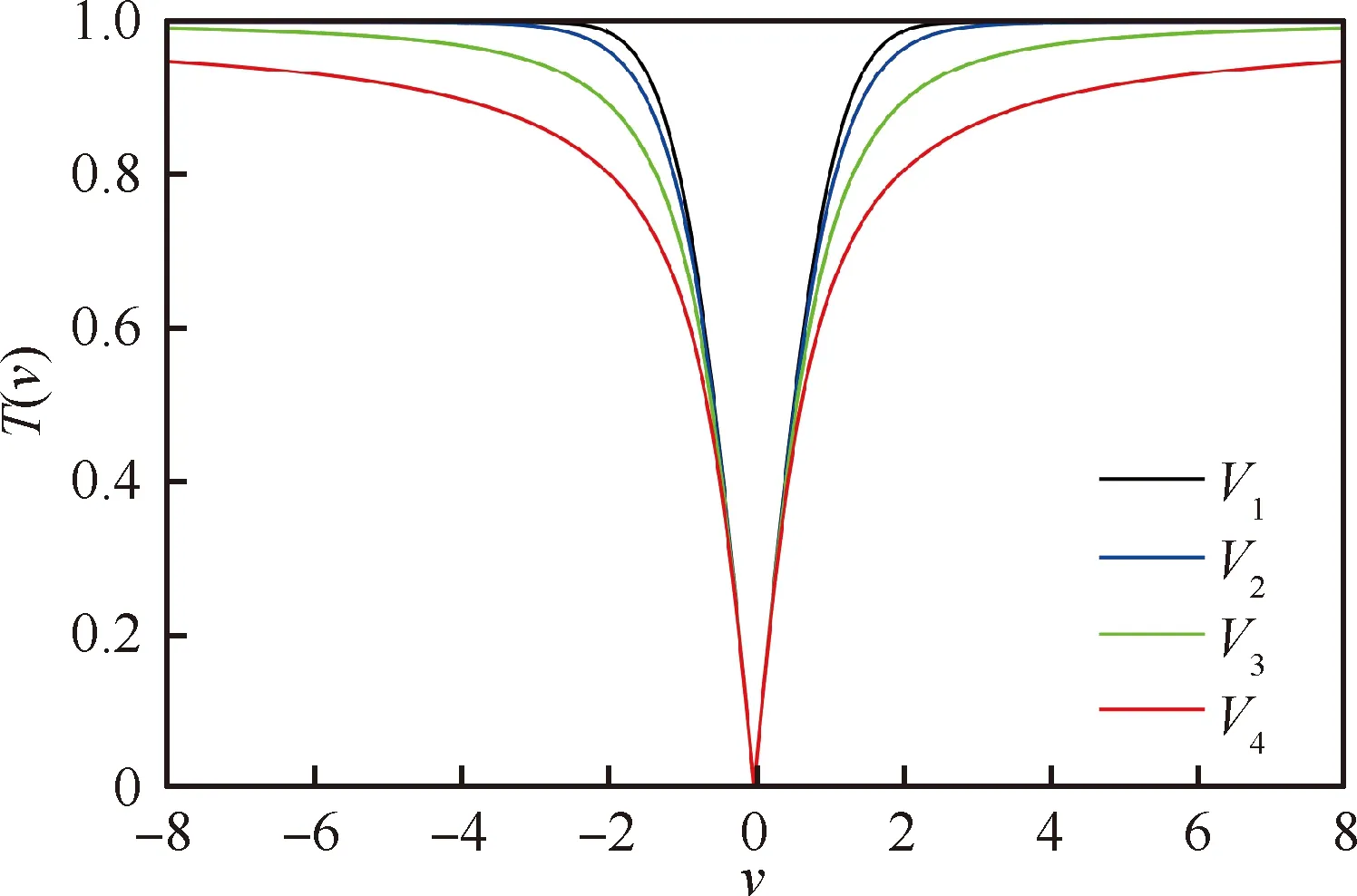
图4 V型传递函数的图像Fig.4 Graph of the V-shaped transfer function

目前已有文献在求解LORA模型时普遍选取S2(sigmoid函数)作为传递函数，本文通过仿真发现选择V4作为传递函数时，算法收敛性和稳定性表现最优。如图5和图6所示，为针对同一优化问题且参数设置一致时，分别选择8种传递函数得到的收敛曲线。从图中可看出，V型传递函数对应维修成本(均小于2×105)整体上小于S型传递函数。

图5 S型传递函数对应的收敛曲线Fig.5 Convergence curves of S-shaped transfer function

图6 V型传递函数对应的收敛曲线Fig.6 Convergence curves of V-shaped transfer function

为详细比较传递函数对算法的影响，分别选取8种不同传递函数，在相同优化问题和参数设置下，各自进行50次优化仿真，统计结果如下表7所示。

表7 选取不同传递函数时的优化结果

Table 7 Optimization results of different transfer functions

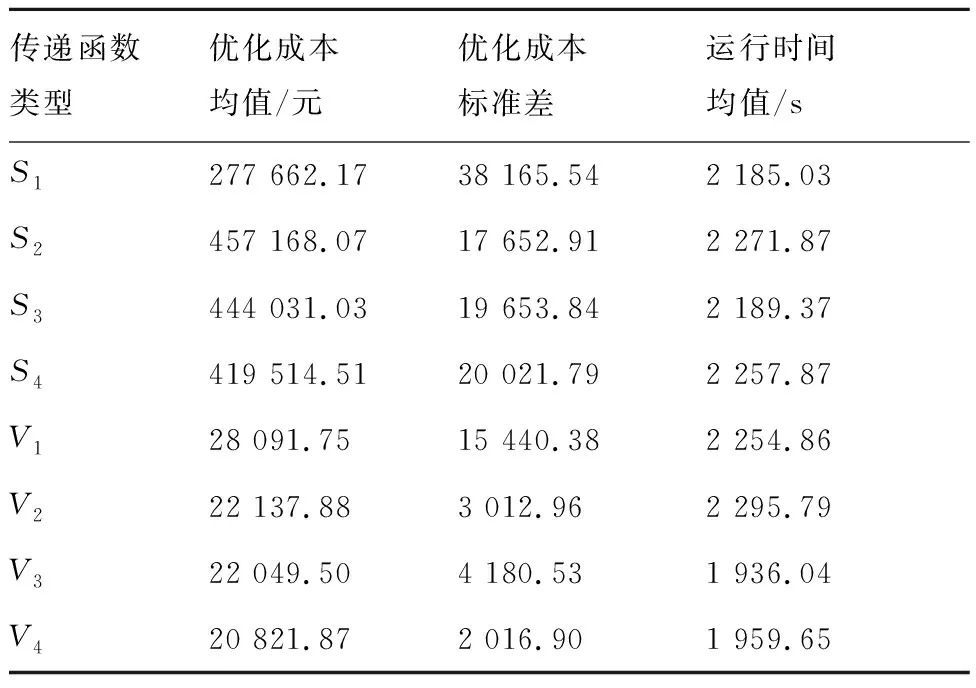
传递函数类型优化成本均值/元优化成本标准差运行时间均值/sS1277 662.1738 165.542 185.03S2457 168.0717 652.912 271.87S3444 031.0319 653.842 189.37S4419 514.5120 021.792 257.87V128 091.7515 440.382 254.86V222 137.883 012.962 295.79V322 049.504 180.531 936.04V420 821.872 016.901 959.65

从表7中可以看出，不同传递函数对应的程序运行时间均值比较接近；而采用V4作为传递函数时，优化成本的均值和标准差均为最小，说明选择V4作为传递函数时，算法的收敛性和稳定性最好。

4 算例分析

现有文献中的LORA模型仅考虑单故障模式的情况，无论具体的故障模式如何，每种类型的组件只需做出一种决策，而本文建立的模型在多故障模式的情况下也是适用的。假设LRU=parent(SRU1,SRU2),其中，SRU2有3种故障模式，同一待分析项不同的故障模式允许在不同的级别实施维修。这必然会影响到资源分配及成本的预估，进而使得全局变量的决策发生改变。解决方法为，可以将每一种故障模式作为一个虚拟维修单元，即LRU=parent(SRU1，SRU21，SRU22，SRU23),统计虚拟维修单元的各级成本，参与LORA决策。

在对模型进行验证时，成本数据设置参考文献[8,10,13]的做法。用一组人为设置的数据来模拟真实情形，在文献[10]的数据基础上增加了维修设备集、多故障模式等类型的数据。本文用于分析的系统包含5个LRU，分为4个部件共享集，如表8所示。其中，待分析项(2,1,2)、(3,2,0)和(3,2,1)分别存在2种故障模式。在不考虑约束条件时，本算例中共有232×7种可能的决策方案。

表9详细列出了待分析项在不同失效模式下，各级别执行不同修理选项的成本及对应故障率。

使用MATLAB语言在台式电脑上实现模型求解。程序运行环境为：MATLAB R2014a、4 GB内存、Pentium(R)Dual-Core CPU 3.2 GHz处理器。算法中参数设置为：粒子总数为200；最大迭代次数tmax=1 400；惯性权重wmax=0.9，wmin=0.4；学习因子c1=c2=2；惩罚函数中k0=0.9。

表10为程序运行后得到的最优决策方案,对应成本为18 591.22元。其中，星号标记部分为子单元因父单元的移动和报废而被迫产生的跟随行为，通过跟随行为矩阵N*滤除，不参与成本计算。图7给出了优化过程中维修成本随迭代次数的变化。

表8 部附件维修共享设备集合

表9 各级别决策成本Table 9 Decision cost of different levels

以代号为(3,2,1)的SSRU为例，表7中对应决策结果的实际含义为

1) (3,2,1)在第1种故障模式下，随LRU(3,0,0)从航线拆下，经车间移动至基地，父单元LRU(3,0,0)和SRU(3,2,0)在基地维修，(3,2,1)在基地报废。

2) (3,2,1)第2种故障模式下，随LRU(3,0,0)从航线拆下，经车间移动至基地，父单元LRU(3,0,0)和SRU(3,2,0)及子单元(3,2,1)均在基地维修。

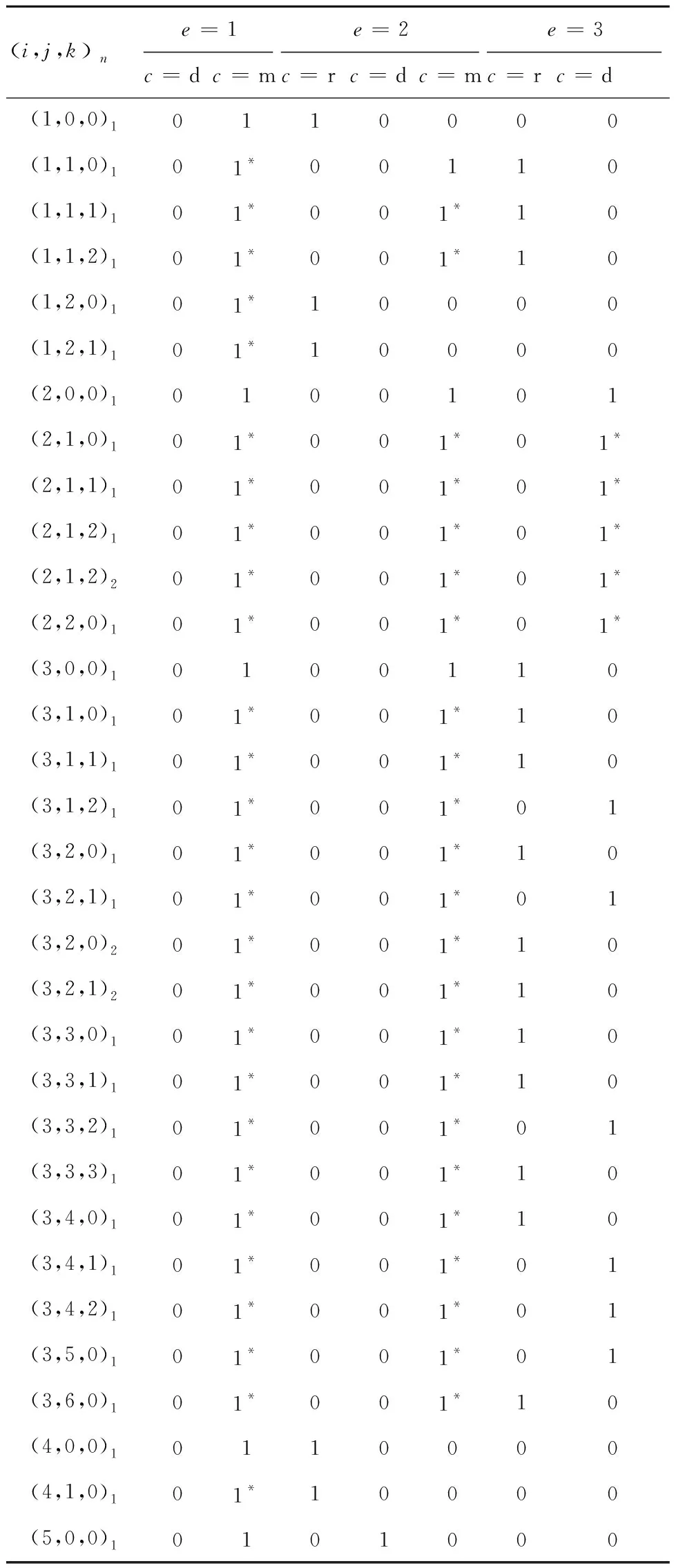
表10 修理级别分析的决策结果Table 10 Decision results of LORA

图7 维修成本随迭代次数的变化Fig.7 Variation of maintenance costs with number of iterations

通过决策流图方法[25]可以直观地表现表10中的决策结果。决策流图的基本单元包括：

1) 决策节点：图8(a)为决策源点，表示故障发生后分析开始；图8(b)为决策截点，表示由于工程约束决策终止。

2) 转换节点：由待分析项名称(i,j,k)、修理级别e、修理决策c等3项信息构成。在本文提出模型中，选择移动或报废2种决策均将零部件作为一个整体来分析，只有选择修理选项时，将待分析项作为多层结构处理，采用如图8(c)所示的结构表示，否则采用如图8(d)所示的单层结构。

3) 决策选项：本文为了表示零件多层结构的关系，基于原有的r-修理、d-报废、m-移动维修3种基本决策，增加了s-分层选项，如对多层级结构选择修理选项，需要使用s决策逐级分解、决策至单层结构，直至分析终止。选择r、d、m 3种决策会产生费用，s决策不产生费用。

图9为三层三级保障体系下的修理级别决策流图。以SSRU(3,2,1)的第一种故障模式为例，根据表10决策结果，其最佳修理方案可用加粗线条标记决策流描述。

图8 决策流图的基本单元Fig.8 Basic unit of decision flowchart

图9 三层三级LORA决策流图Fig.9 Decision flowchart of LORA with three- indenture and three-echelon

5 结 论

1) 本文模型考虑了无故障发现事件和二次维修等人为因素以及通用维修设备对决策的影响，所建立的模型更加符合工程中的实际情况。此外，本文在模型求解部分详细讨论了具有复杂结构的待分析项约束条件处理、惩罚函数的建立、边界条件选择和传递函数选择等技术细节，发现复杂模块拆分及等概率均匀生成决策的方法对处理大规模修理级别分析问题十分有效。

2) 仿真结果表明，跟随矩阵N*在决策中能对父单元选择移动或报废决策而导致的子单元跟随行为进行标记，解决了复杂系统中因层级结构嵌套而引起的维修成本重复累加问题，所得决策方案的预估成本更为准确。

3) 通过对比多次仿真结果发现，传递函数对二进制粒子群算法的收敛性和稳定性有重要影响：V型传递函数较S型传递函数更利于算法收敛，且在选择函数V4时效果最好。

4) 通过算例分析验证了模型的合理性，对由5个LRU、4个部件共享集合所组成的系统进行仿真求解，获得了其中32个部件分别在航线、基地、车间上的维修决策，在求解过程中，维修成本从算法迭代开始时的8.0×105元逐渐减小到1.9×104元，最终得到在所给维修成本基础数据下的最小维修成本为18 591.22元。优化仿真结果显示出本文算法具有良好的收敛性和稳定性，且算法求解效率较高，具有一定的工程实用价值。