基于船舶减速的单线航道通航效率评价

杨 星， 王晶尧， 刘克中， 杨旭刚

(1.武汉理工大学 a.航运学院； b.内河航运技术湖北省重点实验室， 武汉 430063； 2.舟山市港航管理局 岱山分局， 浙江 舟山 316200)

单线航道是港口航道的重要组成形式，其通常是指航道宽度不满足船舶会遇，同一时间仅允许船舶沿单一方向行驶的航道。单线航道相比双线航道更易成为制约航道通航效率的瓶颈。[1-2]在理想状态下，船舶以无相互干扰的自由航行状态通过航道[3]，但实际上由于单线航道内不同大小和种类的船舶航速存在差异，船舶在航道内会相互干扰并可能导致后续船舶采取减速措施以保证安全航行间距。船舶在单线航道内因相互影响而发生减速可看作是对船舶自由航行状态的一种干扰或是对航道通航效率的一种影响。[1,4]探索船舶减速对航道通航效率影响程度和规律对于优化船舶交通组织，提高通航效率具有重要的支持作用。航道通航效率是评价航道运行状态的重要参数，由于不同学者的观点和考虑的角度不同，其对通航效率的解释和处理也有所差别。目前，尚无航道通航效率的标准定义，根据研究对象将通航效率η定义为一定时间内船舶实际航行距离与自由航行状态预期航行距离之比。

当前对航道η的研究主要是利用排队论、船舶交通流仿真等方法研究航道通过能力[5]、航道利用率[6]、船舶排队长度和等待时间[7]与相关参数之间的变化规律。基于排队论的η研究主要是利用排队论可动态描述随机服务系统中排队特征的优势，将航道交通看作是一个排队系统，从宏观角度研究交通流特征参数和服务规则对通航效率的影响，其往往忽略船舶在实际航行中的相互干扰。[8]基于船舶交通流仿真的通航效率研究主要是抽象船舶在航道与码头之间的运营过程，重点研究参数输入和输出之间的关系，通常不考虑船舶航行状态的变化，对η变化的内在规律和影响机理的研究也不完善。[9-11]现有对航道η的研究主要是从宏观角度对航道通航效率进行评价，对航道内船舶航行状态的评价模型和描述不够精细，特别是船舶航行状态差异对航道η影响机理的研究不足。所以，从船舶航行状态差异对航道η影响的角度构建航道η评价模型是有必要的。这有利于管理部门准确地掌握航道利用水平和η影响因子对通航的影响规律，尽量减小船舶到达规律和船速差异对η的影响幅度，而且有利于管理部门制定相关规定，提高航道资源利用率；同时，还可指导航道设计部门根据预计交通流情况合理地进行航道设计或提出设计优化方案。

本文在对单线航道船舶航速大小、差异和减速参数进行统计分析的基础上，进一步分析船舶减速幅度和减速后的航行历时对船舶通航状态的影响程度，并以此为基础构建单线航道η评价模型，通过Arena软件进行仿真试验研究航道η随船舶减速参数变化的变化规律，从而揭示船舶减速对航道η的影响机理。

1 单线航道船舶减速航程损失分析

对于某船舶如果以自由航行预期速度v0通过航道，该船舶预期通过航道全程L的时间为T0，则L=v0T0。对于沿单线航道航行的船舶而言，若考虑船速差异性，速度较大的后续船舶会逐渐追赶速度较小的前船，当前、后船舶间距逼近安全距离时，后船只能减速以保证航行安全。若船舶在航道内发生减速，则船舶航行历时增大，η降低。航道内船舶减速航行过程见图1。船舶减速航行过程分为以下阶段：

1) 船舶驶入航道至t1时刻，未发生减速，船舶减速幅度和减速后的通航历时均为0，减速航程损失为0，船舶η为1。

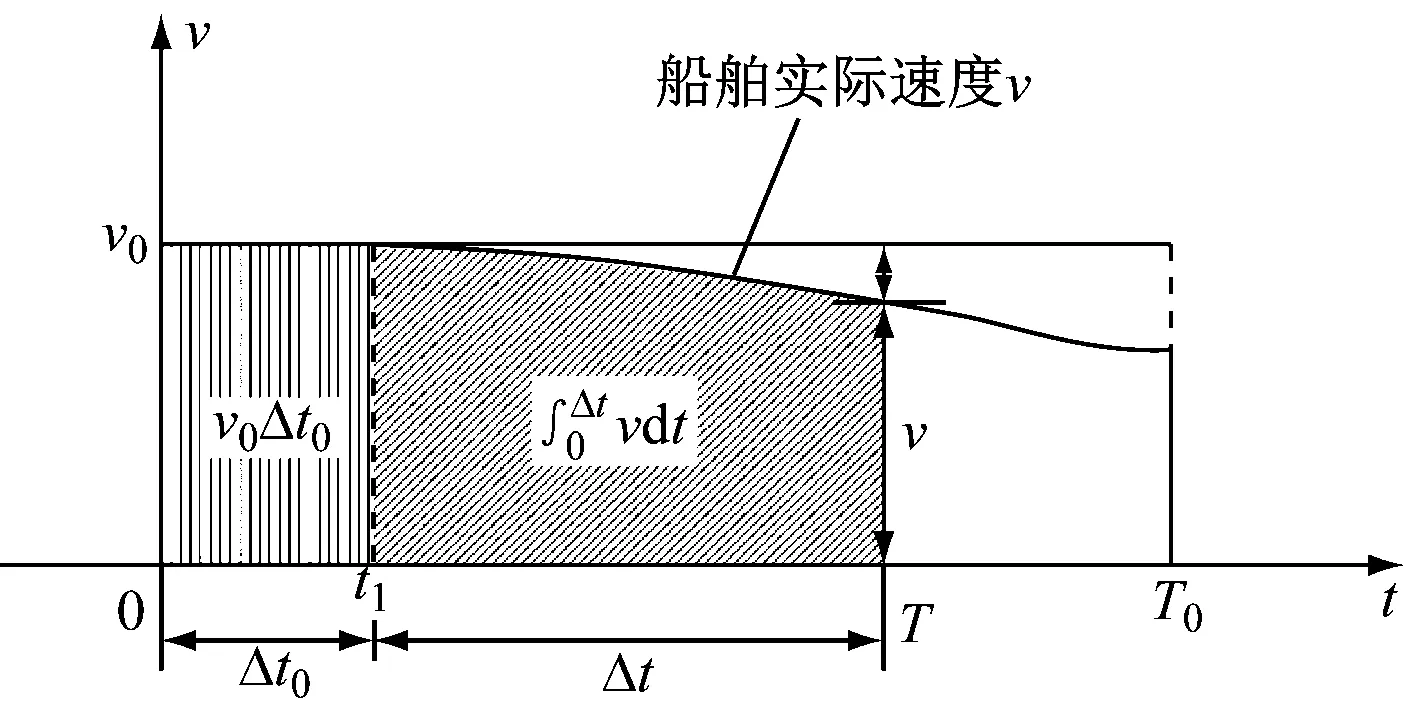
图1 航道内船舶减速航行过程

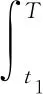
(1)

2 单线航道η评价模型

通过上述分析，船舶减速航行航程损失量为减速幅度对减速航行历时的积分。由此提出基于船舶减速的单线航道η评价模型。

2.1 单船η评价模型

根据前述对η的定义，船舶在航道内η为

(2)

如果船舶实际在T1时刻完成整航道段航行离开航道，有

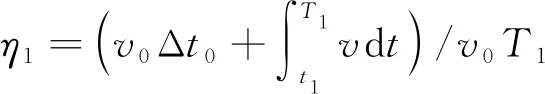
(3)

根据前述对η的定义，航道内船舶通航效率损失Δη是指航道内前后船舶因安全距离约束导致后继船舶因减速造成的船舶航行距离损失量与船舶预期航行距离之比:

(4)

Δη与η的和为1，则通航效率也可表示为

η=1-Δη

(5)

船舶在航道内减速导致的η损失量主要与船舶减速幅度Δv和减速后的通航历时Δt有关，且船舶减速幅度越大、减速后的通航历时越长，船舶减速航程损失量越大，航行状态受船舶减速影响越严重，船舶η越低。如果船舶在航道入口处减速至航速为0，则η亦为0，如果航道堵塞或实施封航管制，航行时间T很大(取决于恢复通航时间)，则航行效率损失很大，η很小。

2.2 多船减速航道η评价模型

单船的η具有较大的随机性，并不能体现航道整体η。可用一定时间内所有通过航道的船舶平均通航效率来衡量航道的通航效率ηc。

船舶在航道内减速可能导致后续若干条船舶呈现追赶前船的态势，并导致后续多艘船舶减速。[12-13]由式(3)可知:在一定时间内n艘船舶减速造成的航道通航效率平均损失量可由不同船舶减速航行的通航效率损失的总和求平均得到，即：

(6)

式(6)中：Δvi指船舶i在减速阶段相对原速度的减速幅度;Δti指船舶i的减速通航历时;T1i指船舶i在航道内的航行时间。在一定时间内n艘船舶通过航道的平均通航效率为

ηnc=1-Δηnc

(7)

3 单线航道船舶交通仿真

3.1 基于Arena软件的仿真框架

船舶交通系统是一个复杂的系统，使用蒙特卡洛方法进行仿真试验，能够很好地体现船舶交通系统的随机性和η的规律性。离散事件仿真软件Arena具有编程工作量小和工作效率高等优势，被广泛应用于船舶交通流仿真试验中。基于Arena软件的单线航道船舶交通仿真模型框架见图2。

图2 单线航道船舶交通仿真模型框架

3.2 交通流数据提取

船舶减速造成船舶和航道η的损失。航道长度和船舶速度大小决定航道η的初始水平，船舶减速幅度和减速通航历时决定船舶航行效率损失情况，两者共同决定了航道的通航效率。相关研究表明：船舶减速受航道长度、船舶到达规律、速度大小和差异性等的影响[12-13]，但针对同一航道来说主要考虑船速分布规律和船舶到达规律的影响。

为准确模拟船舶交通过程，本文选取交通流量较大的虾峙门分道通航制水域2017年8月27日—2017年9月2日的船舶交通流历史数据及船舶交通服务(Vessel Traffic Service, VTS)实际观测情况对船速分布规律和船舶到达规律进行统计分析。虾峙门航道执行分道通航制，船舶按照通航分道进出港航行，就单侧分道而言，在忽略船舶间追越的条件下其通航情形类似于单线航道，可将其视为单线航道提取交通流数据用于仿真分析。

3.2.1船速分布规律提取

船舶速度分布是指船舶航经某一断面时速度服从的概率分布。对经过虾峙门L1报告线的船舶速度进行统计拟合见图3。

由图3可知:船速服从均值μ=10 kn，标准差σ=2.85的正态分布，即v～N(10,2.852)。通过VTS实际观察发现，速度小于4 kn的多为渔船捕鱼漂航所致。

3.2.2船舶间时距统计

船舶间时距指相邻两艘船舶到达某一断面的时间差。对到达虾峙门L1报告线的船舶间时距进行统计分析及数据拟合见图4。

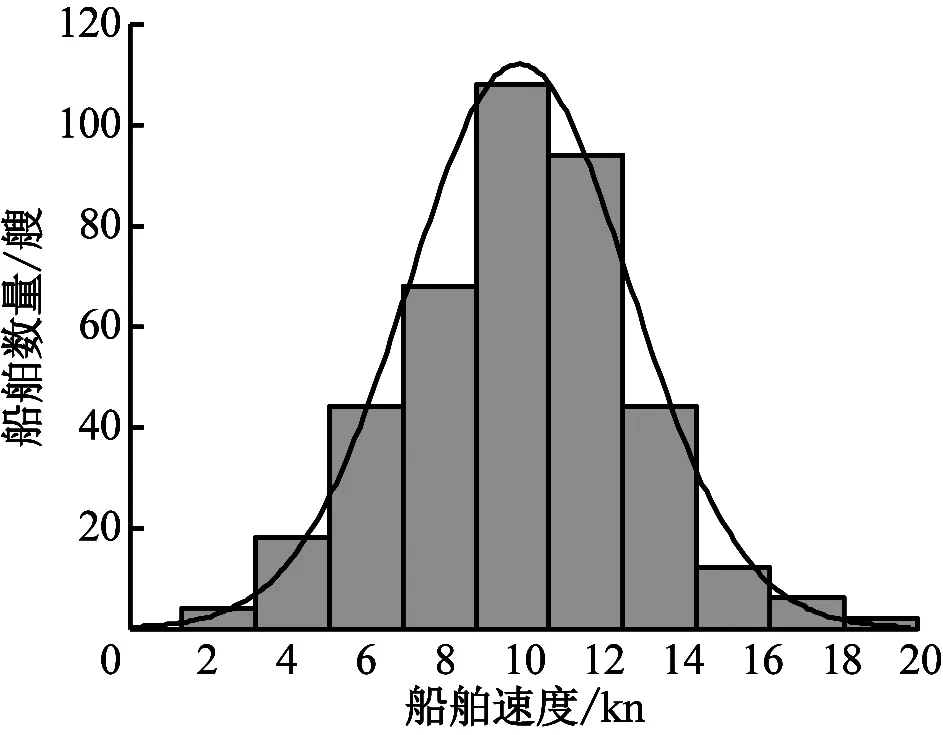
图3 船舶速度分布拟合图

图4 船舶间时距分布拟合图

当用指数分布进行拟合时，其卡方检验值为0.638，这表明船舶间时距服从参数为β的指数分布，此时，指数分布的参数为25，即X～E(25)。由泊松事件的时间间隔与指数分布的关系可知：船舶到达航道入口这一事件服从参数为λ的泊松分布，其中λ被称为到达率[10-11]，即船舶到达服从参数λ=2.4的泊松分布。

从船舶昼夜流量上分析，虾峙门分道通航制水域夜间到达船舶数量约为白天到达船舶数量的1/2。假设船舶夜间到达率λn为白天到达率λd的1/2，全天到达率为昼夜到达率的平均值。

模拟λa=2.4和λd=3.2、λn=1.6时7 d的到达船舶数量，并与7 d实际到达船舶数量进行对比分析，进而验证假设的合理性。船舶到达数量模拟误差分析见表1。

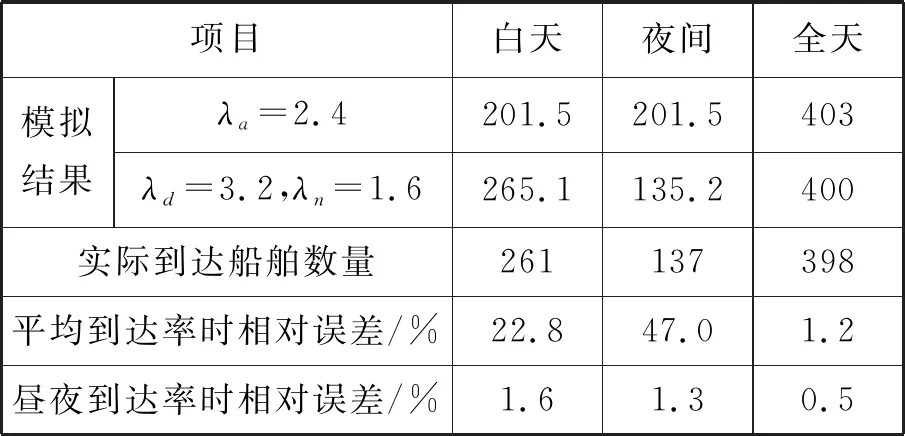
表1 船舶到达数量模拟误差分析

由表1可知:上述假设基本合理，且用平均到达率刻画昼、夜到达船舶数量存在较大误差,而用昼、夜船舶到达率可准确刻画昼、夜到达船舶数量差异和到达船舶总数量。

3.3 仿真参数设置

由于船舶减速行为受航道长度、船舶到达规律、速度大小和差异性等的影响，且船舶到达服从泊松分布，船速服从正态分布,因此，主要研究航道长度L、船舶到达率λ、速度均值μ和标准差σ等参数对航道通航效率的影响。根据实际船舶到达规律、速度分布和航道长度情况，对上述4个参数共设计3组试验。仿真参数设置见表2。

表2 仿真参数设置

表2中:λd为白天到达率，变化区间为[1,5]，λn为夜间到达率，变化区间为[0.5,2.5]，试验中白天到达率λd和夜间到达率λn每隔12 h转换一次；因保持舵效的最小速度为3 kn，故船速最小值设为3 kn。此外，相邻船舶安全间距设为1 800 m，试验时长为30 d，重复20次。每次试验前预热10 h以消除系统初始化对试验结果的影响。

3.4 试验结果分析

在不同速度和航道长度条件下，航道η随到达率λ的变化曲线见图5～图7。

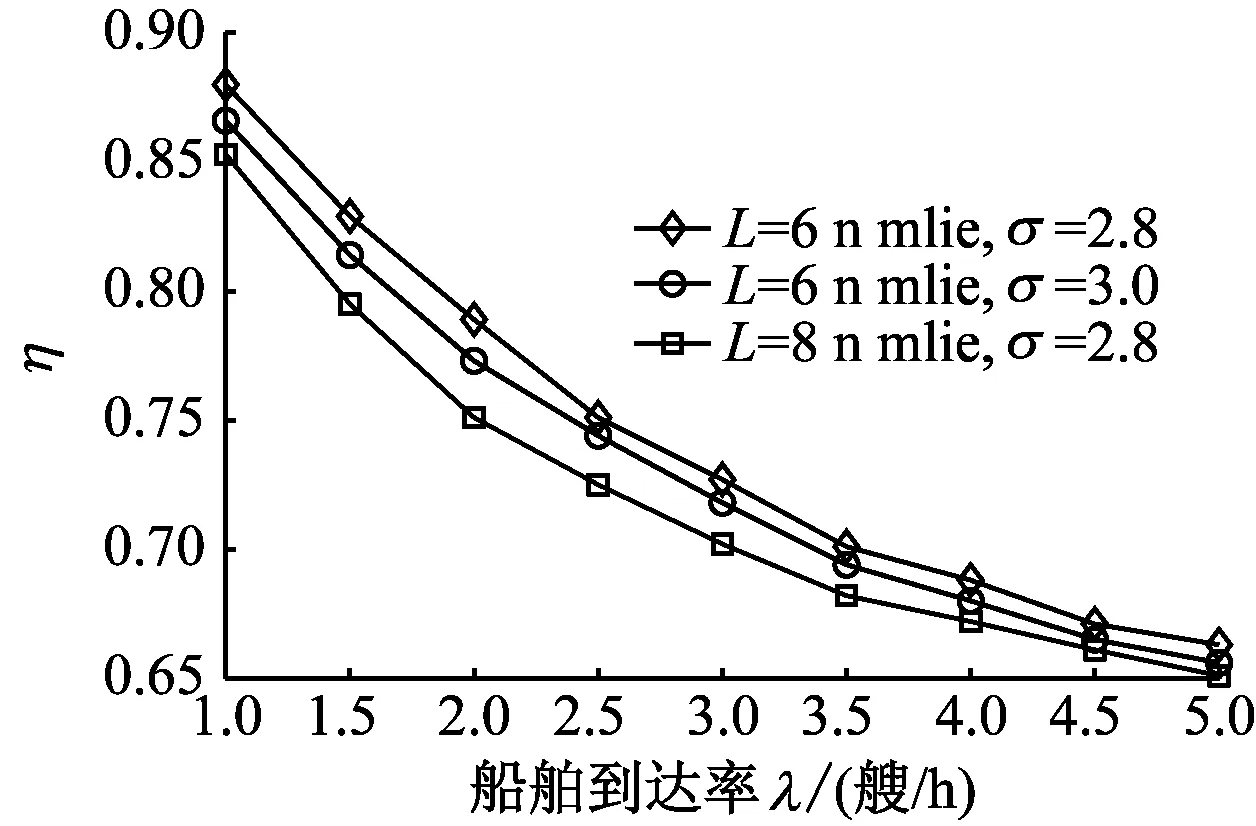
图5 η随到达率变化曲线(μ=8 kn)

图6 η随到达率变化曲线(μ=10 kn)

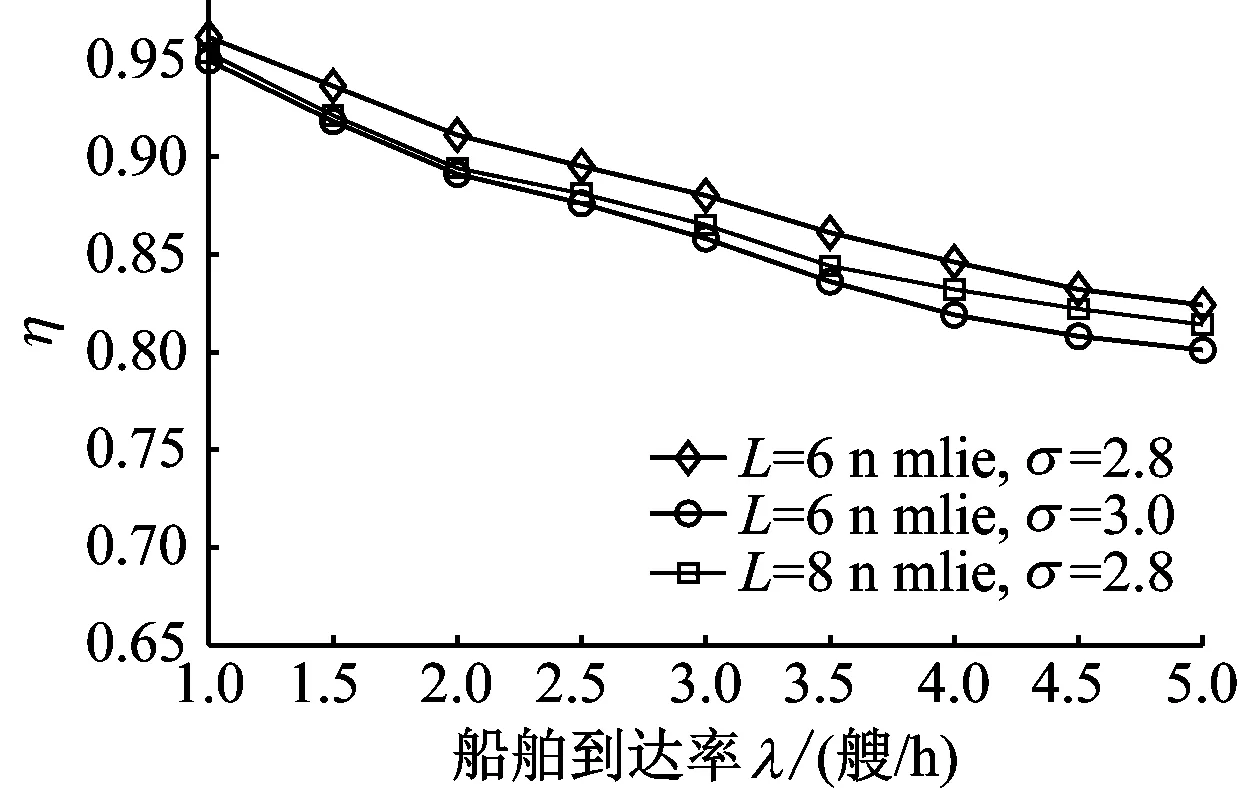
图7 航道η随到达率变化曲线(μ=12 kn)

图5～图7中：航道η是白天到达率λd等于λ，夜间到达率λn等于λ/2对应的航道η值。

从船舶减速对航道η影响的角度看，当船舶到达率增大时，航道η整体呈线性降低趋势。从η曲线变化率看，速度均值越大，η变化越平缓。此外，由图5、图6、图7对比可知:在不同条件下，航道长度和速度差异变化对航道η的影响程度有所不同。μ=8 kn时，航道长度变化对航道η的影响更大；μ=10 kn时，速度标准差和航道长度变化对航道η的影响相当；μ=12 kn时，速度标准差变化对应的航道η降低幅度更明显。航道η总体呈现速度均值较低时对航道长度变化敏感，在速度均值较高时，对速度差异变化敏感的变化趋势。

上述曲线变化的原因是航道长度增加，船舶通过航道的时间延长，此时，船速差异越大，航道内后续船舶追上前船并采取减速的可能性越大，航道η降低越明显。当船舶交通流速度较低时，航道η基本由最小限速决定，因此，速度差异对η的影响较小；相反，当船舶交通流速度较高时，速度差异越大，则交通流整体减速越明显，η降低幅度也就越大。若以航道η=0.8作为调度的临界条件，则当μ=8 kn，λ>2或当μ=10 kn，λ>3时，需要对单线航道船舶通航进行调度以提高航道η。

4 结束语

在分析船舶η损失量与船舶减速位置和减速幅度关系的基础上，用船舶减速幅度和减速通航历时衡量船舶η损失率，进而构建单线航道η评价模型。通过对虾峙门分道通航制水域船舶交通流数据的统计分析，得到影响船舶减速的交通流特征分布规律，以此为基础，结合船舶减速过程，设计蒙特卡洛试验对单线航道η进行研究，并利用离散仿真软件Arena实现单线航道船舶交通仿真，得到船舶减速参数变化对航道η的影响规律。研究结果表明：从船舶减速对通航状态影响的角度，航道η随到达率的增大而减小；在速度较低时，航道η对航道长度变化更为敏感，随着速度的提高，航道η对速度差异变化更加敏感。