基于前景理论的船舶避碰决策优化方法

胡佳颖, 刘克中,b, 吴晓烈,b, 刘炯炯, 杨 星,b

(武汉理工大学 a.航运学院； b.内河航运技术湖北省重点实验室， 武汉 430063)

船舶避碰决策问题一直以来是航行安全领域的热点和难点问题，与船舶自身条件、通航环境和船员素质等诸多因素密切相联。船舶避碰技术经历了从几何方法和雷达到“专家系统”再到“智能避碰”的发展过程。初期，船舶避碰主要采用几何计算方法[1-2]，通过计算船舶间的最近会遇距离(Distance of Close Point of Approaching,dCPA)和到达最近会遇距离的时间(Time to Close Point of Approaching,tCPA)来评估船舶的碰撞危险。近年来快速发展的人工智能技术与方法已克服早期用确定性方法解决避碰决策问题时遇到的抽象因素众多及量化困难等难题，船舶避碰决策的研究方法逐渐由最初的数学计算模型过渡到人工智能方法，如遗传算法[3-4]、神经网络[5]、蚁群算法[6]等。

国内外船舶避碰决策优化的主要方法是以国际海上避碰规则和良好船艺作为约束条件，运用智能化算法，如粒子群算法[7]、克隆选择优化算法[8]和社会情感优化算法[9]等对船舶碰撞危险度和航程损失的多目标函数进行优化。在船舶避碰相关研究中，无论是基于经典几何方法还是智能算法，均存在对船舶航行值班驾驶员主观风险偏好，在碰撞危险度和航程损失所构成的多目标函数中没有体现船员主观差异性，也没有考虑作为让路船在避碰操作中的船舶轨迹平稳性等问题。为此，本文为引入行为科学理论——前景理论，以提出一种能够引入人为风险偏好的船舶避碰决策优化方法为核心目标，构建基于前景理论的船舶避碰决策优化模型，根据文献查阅和海员驾驶经验，选取船舶碰撞危险度、航程损失和轨迹平稳性作为避碰决策优化指标，最后通过典型会遇场景的避碰决策研究和在不同风险态度下船舶避碰决策差异对比分析，总结船舶避碰决策与人为风险偏好之间的联系。

1 基于前景理论的避碰决策优化模型

船舶避碰决策过程中涉及很多因素，如通航环境、安全会遇距离(SDA)、转向幅度等，这些因素与船舶驾驶员的驾驶技能和良好船艺存在关联。根据长江口水域船舶会遇冲突提取与避碰关键参数分析，在相似的会遇场景下，让路船舶的转向时机和转向幅度不同，DCPA的分布也从0.1～4.0 n mile不等，因而船舶避碰决策存在着极大的个体差异性。综上所述，研究船舶避碰决策和优化，需要将人的风险偏好考虑进来，研究在不同风险态度下船舶驾驶员最优决策的差异性。前景理论提出不同的风险系数反映出决策者不同的风险态度，而不同的风险态度导致决策结果的差异。因此，本文利用前景理论来解决船舶避碰过程中船舶驾驶员因风险态度不同而引起的决策差异。通过设置不同的风险态度参数来反映船舶驾驶员的风险态度，以风险决策模型中的参数的变化来研究驾驶员在同一会遇场景下的避碰决策变化情况。

1.1 模型总体框架

本文构建的基于前景理论的两船避碰决策优化模型主要分为两部分：

1) 对生成避碰方案的决策信息矩阵进行规范化处理和灰关联分析，进而利用前景理论获得正负前景价值矩阵。

2) 通过目标规划求取最优指标权重，代入综合前景价值公式中得到每个备选避碰方案的综合前景价值，从而进行避碰方案选择。避碰决策优化分析框架见图1。

1.2 避碰决策矩阵规范化处理与灰关联分析

假设根据避碰规则在避碰决策优化问题中共生成了n个安全可用的避碰方案，组成避碰方案集U={U1,U2,…,Un}，m个指标组成指标集A={A1,

图1 基于前景理论的避碰决策优化分析框架

A2,…,Am}，则可选避碰方案集U对应的指标属性集A的决策选择样本矩阵X为

(1)

因为前景理论主要针对得失心理，为消除不同指标的量纲，采用规范化处理方法[-1,1]线性变换算子，从而得到一致性效果规范化R。规范化处理的基本原理是对优于平均水平的指标值赋予[0,1]的正数，对劣于平均水平的指标值赋予[-1,0]的负数。

令

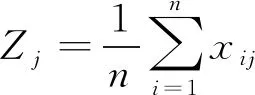
(2)

成本型指标(其值越小越好的指标类型)的规范化处理方式为

(3)

效益型指标(其值越大越好的指标类型)的规范化处理方式为

(4)

以上变换就是[-1,1]线性变换算子。

根据规范化矩阵R，设：

j=1,2,3

(5)

由灰关联决策方法可知第i个备选方案与正负理想方案关于指标Aj的关联系数分别为

(6)

(7)

1.3 方案的综合前景价值

文献[11]和文献[12]在大量行为科学试验的基础上修正期望效用理论，提出前景理论，用于描述和预测人们在风险决策中的行为，之后又发展为累积前景理论。前景理论认为风险决策在很大程度上取决于决策主体是关注收益还是损失、风险态度的水平是保守还是冒进，并根据前景价值的大小选择方案。

价值函数是决策者根据对真实值主观感受形成的价值。根据文献[12]可知避碰方案Ui的各指标对应的前景价值函数为

(8)

式(8)中：参数α和β分别为在参考点右侧(收益)和左侧(损失)价值函数的凹凸程度，0<α<1，0<β<1，代表不论是收益还是损失，都存在敏感性递减的现象；θ为决策者的损失厌恶程度，θ>1为决策者是损失规避的。

由式(8)可得：避碰方案Ui关于指标Aj的正前景价值记为

(9)

负前景价值记为

(10)

根据文献[12]，概率权重是决策者根据事件结果出现的概率ω而做出的某种主观判断，其并不是概率ω，决策者面对收益和损失时的概率权重函数的表达式为

π(ω)=

(11)

式(11)中：γ和τ分别为在参考点左右两侧概率权重函数的拟合参数。文献[12]通过大量的试验研究和参数拟合表明：α=β=0.88，θ=2.25，γ=0.61，τ=0.69与实际经验较为一致。

则避碰方案Ui的综合前景价值为正负前景价值之和：

(12)

对备选方案进行方案排序需要对决策指标的权重进行计算，为获取最大综合前景价值，设指标集的权重向量ω=(ω1,ω2,…,ωm)，把避碰决策中的指标权重的取值范围作为目标规划的约束条件，最大综合前景价值作为目标，求解最优解即为最优评价指标权重：

(13)

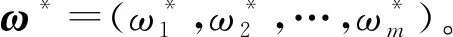
将求得的最优指标权重ω*代入式(12)，方案的最优综合前景值为

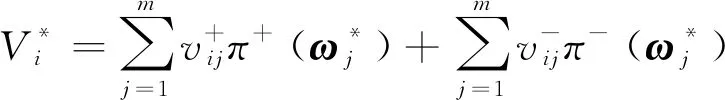
(14)

最后比较各避碰方案的综合前景价值并按从大到小排序，即为避碰方案优劣排序。

2 会遇场景设计及避碰决策指标选择

2.1 会遇场景设计及避碰方案生成

为验证模型的可用性和有效性，分析船舶驾驶员的风险态度对避碰决策的影响，需要对会遇场景的避碰进行仿真生成避碰决策，并利用本文模型进行决策优化。根据已掌握的具有代表性的实船信息，设计一个典型交叉会遇场景。

以一艘长225 m，7.6万t的满载散货船舶为模拟对象，假设本船舶以15 kn的航速航行，航向为000°，目标船舶以13 kn的航速航行，航向为287.75°。此时，海上能见度良好，本船驾驶操纵状况良好，当本船与目标船相距6 n mile时，发现与目标船形成交叉态势，存在碰撞风险，此时的DCPA为0.03 n mile，且本船舶为让路船舶，故采取转向避碰策略，本船舶与目标船舶的运动参数见表1，T0为船舶满舵旋回转向90°所需时间，k为系数，一般取(1.5,2.0)，为保证安全,取k=2.0，具体可参考文献[13]。

表1 本船舶与目标船舶会遇的运动参数

根据会遇态势和船舶运动参数，使用MATLAB程序仿真可得船舶具体的避让方案。为更好地分析不同风险态度下驾驶员的决策行为，在生成避碰方案时分别设置SDA=1.0 n mile、1.2 n mile、1.4 n mile、1.6 n mile、1.8 n mile、2.0 n mile，并据此分别生成带有转向时机和转向幅度的避碰方案。

本文研究的是在不同风险态度下船舶驾驶员在可接受碰撞风险和避碰决策代价的平衡。如果SDA越小、转向时机越晚，那么船舶碰撞风险越高，但是避碰造成的航程损失会更小，转向过程中船舶更平稳。为更好地凸显方案之间的差异性，在生成避碰方案时，从SDA较小的方案中选择转向幅度小和避让时机较晚的方案，从SDA较大的方案中选择避碰转向幅度较大、行动时机较早的方案，这样方案之间的区分度就会更明显。

2.2 避碰决策指标

船舶避碰决策主要是依据《国际海上避碰规则》和海员经验做法确定会遇态势和局面，求取让路船舶和直航船舶的避让幅度与时机、复航时机的过程。对避碰决策优化主要体现安全性、经济性和轨迹平稳性等3个方面，其中安全性是避碰决策优化的前提。

1) 从安全的意义上讲，就是避碰措施必须遵守《国际海上避碰规则》。

2) 从经济的意义上讲，体现在避让时机、施舵角和幅度的量化与优化问题上，使避碰结束时，本船的航程损失达到最小。

3) 从轨迹平稳的意义上讲，体现在让路船在改变航向和航速进行避碰时尽可能能保证船舶的平稳。

因此，选取船舶碰撞危险度、航程损失和船舶轨迹曲线平滑度作为优化决策的指标。

3 风险偏好差异下的决策对比分析

3.1 避碰决策优化过程

根据避碰方案信息和决策指标，参考文献[14]中的船舶碰撞危险度模型、文献[7]中的航程损失模型和轨迹平稳性模型，可得避碰决策样本矩阵X。其中:船舶碰撞危险度和航程损失为成本型指标;平稳性为效益型指标，对避碰决策样本矩阵X进行规范化处理，得到规范化矩阵R。

(15)

由式(15)可知:正理想避碰方案为U+={0.503,0.901,1};负理想避碰方案为U-={-1，-1，-0.909}。

根据式(6)和式(7)分别计算各个方案的正负关联系数矩阵为

(16)

(17)

根据式(9)和式(10)分别计算各避碰方案的正、负前景价值矩阵为

(18)

(19)

以避碰方案的综合前景价值最大化为目标，建立优化模型：

(20)

(21)

求得最优解ω*={0.5,0.4,0.1}。

将避碰方案的综合前景价值由大到小排序，便可得到各避碰方案的优劣排序为

U1≻U2≻U3≻U4≻U5≻U6

(22)

由式(20)可知：方案U1的综合前景价值最大，因此在6组备选的避碰方案中，最优避碰为方案U1。

为研究不同风险偏好的驾驶员在船舶避碰决策中的差异，参考其他学者关于前景理论的研究成果，按照上述方法再分别计算风险中性和风险态度保守时的最优避碰方案决策，得到的结果为

避碰方案的优劣排序为

U3≻U4≻U6≻U2≻U5≻U1

(23)

由式(23)可知：最优避碰方案为U3。

避碰方案的优劣排序为

U6≻U5≻U4≻U1≻U3≻U2

(24)

由式(24)可知：最优避碰方案为U6。

3.2 不同风险态度下避碰决策差异对比分析

本文所提出的优化方法是基于船舶驾驶员的风险态度来平衡碰撞危险度、航程损失和平稳性等3个指标，构建多目标决策模型，并求得最优避碰方案。当船舶驾驶员是风险偏好型时，驾驶员认为碰撞危险度指标的权重要小于风险中性和风险保守的情况，而风险中性时的碰撞危险度权重也小于风险保守时的权重。

不同风险态度下避碰方案的综合前景价值折线图见图2。根据计算结果和图2可知：在不同风险态度下，对于同一避碰场景的相同的避碰方案前景价值不同，在风险偏好和风险中性的情况下的避碰方案的综合前景价值比风险态度保守时更大；在不同风险态度下，安全性、经济性、轨迹平稳性等3个指标的权重的变化导致风险偏好情况下方案的综合前景价值逐渐减小，甚至小于风险中性下的风险偏好。

图2 不同的风险态度下避碰方案的综合前景价值折线图

6组方案中碰撞危险度、经济性、轨迹平稳性之间的关系有：

1) 当驾驶员为风险偏好型时，避碰最优决策方案更倾向于碰撞危险度较高的避碰方案，方案综合前景价值排序为

U1≻U2≻U3≻U4≻U5≻U6

(25)

基本符合碰撞危险度较大的方案优于碰撞危险较小的方案。

2) 船舶驾驶员在保守的风险态度下，3个指标之中对于安全性的要求最高，安全性指标的权重也是3种风险态度中最高的，当在进行最优避碰方案选择时，更倾向于碰撞危险度较低的方案，对经济性和平稳性的要求适当放低，方案优劣排序为

U6≻U5≻U4≻U1≻U3≻U2

(26)

式(26)也印证了这一观点。

3) 当船舶驾驶员的风险态度为风险中性时，对于最优避碰方案的选择则更倾向于3个指标都比较均衡的避碰方案，既不会过于追求平稳性和经济性方面的优势忽略了碰撞危险度水平，也不会舍弃经济性和平稳性选择碰撞危险度小的方案。

4 结束语

本文针对避碰决策优化研究中对驾驶员的风险偏好考虑不足的问题，提出基于前景理论的避碰决策优化模型。根据船舶驾驶员不同的风险态度，对同一会遇场景下的避碰决策进行优化，并分析船舶避碰决策与驾驶员风险态度之间的关联性。案例分析结果表明:本文建立的优化模型能够很好地反映船舶驾驶员在不同风险偏好下的避碰方案选择情况，符合经验做法。前景理论在避碰领域中具有有效性和可用性，将行为科学理论引入到船舶避碰领域，能够为船舶智能避碰决策拟人化提供支持。