上新世红土微观结构参数与渗透系数的变化关系研究
2020-04-15杨玉茹李文平王启庆
杨玉茹,李文平,王启庆
(中国矿业大学资源与地球科学学院,江苏 徐州 221116)
新近系上新世(N2)红土是一种主要分布于我国西北地区的区域性特殊土,沉积于浅层含水层之下,是西北浅埋煤田开采的直接隔水层,是保水采煤和环境保护的关键隔水层[1]。近年来,随着我国对西北煤炭资源的开发,众多学者对红土开展了大量研究,曲永新等[2]通过对西北滑坡的调查,探讨了N2红土的物质成分、工程特性与滑坡的关系,指出红土是区域典型滑坡的滑动带;阴静慧等[3]通过野外工程地质调查和室内土工试验,研究了N2红土物理性质及其成因;李涛等[4]利用三轴试验研究了采动前后N2红土隔水性的变化及环境效应;李文平等[5-6]通过三轴蠕变试验和水土相互作用试验,研究了采动破裂红土的渗透性变化,提出N2红土具备隔水层再造的工程地质属性。上述针对红土工程地质性质的研究主要从宏观角度进行。
大量事实表明,土的工程性状在很大程度上受到其微观结构系统的控制[7]。著名土力学家沈珠江院士[8]曾指出:土的结构性问题是21世纪土力学的核心问题,土体微观结构直接或间接影响着岩土体宏观物理性质,研究微观结构有助于解释其宏观工程特性。杨爱武等[9]研究了吹填土蠕变过程中微观结构的变化特征,解释了吹填土蠕变现象的微观本质为吹填土内部结构随着外力的变化不断自我调整再造的过程;吴凯等[10]通过统计学方法建立了压实黄土孔隙微观结构量化参数与侧限压缩、直剪强度的关系;侯超群等[11]定量研究了不同浸水时间下膨胀土微观结构的演变过程,揭示了膨胀土吸水膨胀的机理;李喜安等[12]通过室内渗透、渗气试验、基本物理试验和扫描电镜分别得到原状和重塑马兰黄土的渗透系数、孔隙比和微观孔隙参数,利用数学模型建立了宏-微观孔隙参数与渗透系数之间的关系。但目前对于N2红土微观结构与渗透性关系的研究还较少。
本文利用Quanta 250扫描电子显微镜拍摄不同渗透系数的红土样的SEM图像,并通过Matlab对图像进行处理和定量分析,获得N2红土的微观结构参数,建立了微观结构参数与渗透系数之间的关系。该研究结果可为工程实践中N2红土渗透性变化规律提供理论参考。
1 试验内容
1.1 试验样品
试验红土取自陕北榆林地区,野外出露红土主要为浅棕红色。通过钻探取样,结合室内土工试验,得到4个土样的基本粒度组成(图1),物理力学性质见表1。
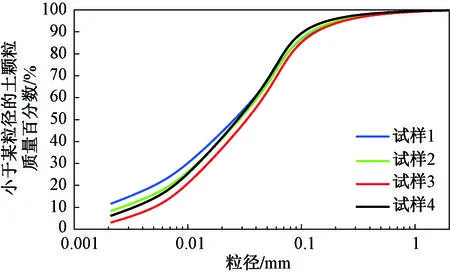
图1 N2红土粒径级配累计曲线Fig.1 Particle-size distribution curve of N2 laterite

表1 N2红土基本物理力学性质Table 1 Basic physical properties of N2 laterite
根据图1可知,试样N2红土黏粒和粉粒(<0.075 mm)含量占所有粒径的80%以上,土颗粒的不均匀系数较小(Cu<5),说明N2红土的粒径较为均匀。天然状态下N2红土呈硬塑至坚硬状态,具有较强的膨胀性,属于中高压缩性土。
1.2 试验方法
采用室内变水头试验对试样的天然渗透性进行测试,并依据式(1)计算出红土的渗透系数(表2)。

(1)
式中:K——渗透系数/(cm·s-1);
a——刻度管截面积/cm2;
L——试样径流长度/cm;
A——试样截面积/cm2;
t1,t2——起始和结束时刻/s;
H1,H2——t1和t2时刻水头/cm。
选取不同渗透系数的代表性土样,采用Quanta 250扫描电子显微镜对土样进行微观结构测试。具体试验过程如下:(1)制备观测样品。对选取的土样进行编号,制备尺寸约Φ10 mm×10 mm的圆柱状样品,同时保证试样断面新鲜,避免微结构的破坏。(2)样品干燥。利用ZK-82型真空干燥箱将土样干燥24 h,彻底去除土中的水分。(3)样品喷金。为防止拍摄过程中样品受到电子束的轰击而产生放电现象,在样品表面镀一层金,然后用导电胶将土样固定在样品台上,防止样品抖动。(4)将制备好的试样放入扫描电镜内进行拍照观察。拍照时先用高倍找到典型的“结构单元体”,再逐步降低放大倍数,保证图像清晰度并获取足够的信息量。(5)利用Matlab软件编制程序,对SEM图像进行二次处理及图像信息分析,从而得到N2红土的微观结构特征。
1.3 试验结果
根据SEM图像(图2),N2红土颗粒骨架主要呈分散状态,其间有黏粒充填,胶结良好。孔隙分布均匀,形态不规则,孔壁发育少量黏粒。微观结构主要呈絮凝胶状,局部可见大孔隙,颗粒连接形式主要为边-边接触和边-面接触,接触面积较大,土体结构稳定。骨架颗粒表面有形状不规则的凝胶颗粒和孔隙。

图2 N2红土的SEM图像(放大2 500倍)Fig.2 SEM image of N2 laterite (2 500 times of magnification)
2 微观结构图像处理
土体的微观结构指微孔隙(结构单元体)的大小、形状、定量比例及相互作用方式[13]。借助分析软件可以定性描述、定量分析微孔隙的结构特征。Matlab又称矩阵实验室,可通过调用一系列处理函数进行计算,实现对用矩阵像素记录的图像的快速批量处理,工作效率高,经常用于土体微观结构分析[14]。本次研究借助Matlab对N2红土的SEM图像进行分析处理。
2.1 图像预处理
针对多数图片存在的对比度不高、噪声多、亮度不均匀等问题,首先对图像进行预处理。将SEM图像读入Matlab中,把图像转化为矩阵的形式。为了避免对图像孔隙的提取造成影响,使用imcrop函数将SEM图像底部的图像信息记录栏裁去。针对图像亮度不均匀情况,使用disk圆盘形均值滤波器估计不均匀背景,并使用图像运算功能去除不均匀背景;针对对比度不高的情况,使用imadjust函数调整对比度;为了拉大像素间差距,表现更多细节,采用imhist函数对图像进行直方图修正;针对图片噪声过多的问题,使用Matlab的小波工具箱对图像进行降噪处理,分解层次N=2,选用Sym4小波。经过预处理后的N2红土SEM图像如图3所示。

图3 SEM图像预处理Fig.3 SEM image preprocessing
2.2 图像分割及优化
为了把土样的颗粒和孔隙区分开,需要对预处理后的图像进行分割,即图像的二值化。常见的分割方法包括迭代算法[15]、Oust算法、分水岭算法和P-参数法等[16]。
迭代算法和Oust算法仅考虑图像本身的灰度值,分割时会出现大块的黑色区域,导致附着在红土大颗粒上的黏粒信息丢失(图4a~b)。分水岭算法是一种数学形态学方法,主要是基于拓扑理论对图像进行分割,对物体的微弱边缘响应较好。由于红土存在大量黏粒,使用分水岭算法容易造成过度分割的现象(图4c)。P-参数法是先确定一个阈值,然后统计观察目标在图像中所占的像素比例,不断调整阈值直到比例满足要求。
由于N2红土含有大量黏粒,为了避免微小孔隙信息丢失,本次研究采用P-参数法选择阈值。首先使用迭代法自动确定阈值,对图像进行分割,发现有许多土颗粒被识别为孔隙,以10为单位逐渐减小阈值到刚好可以识别出孔隙中的微小颗粒[17]。处理后的图像如图4(d)所示。由于土颗粒不平整,存在毛刺,处理后图像存在很多黑色麻点,采用形态学开闭运算滤除麻点,这样既不改变颗粒或孔隙的结构,又使孔隙边缘清晰可见,方便后续孔隙结构参数的提取,处理结果如图4(e)所示。
2.3 微观参数提取
土体的微观参数包括颗粒的几何参数和孔隙的几何参数,本研究主要侧重于孔隙的几何参数。Matlab中用于提取边缘的主要有Roberts算子、Laplacian算子和bwperim函数等[18]。本研究采用bwperim函数对孔隙边缘进行了提取,如图4(f)所示,孔隙结构明显,边界清晰。使用regionprops函数对孔隙的几何参数进行提取,包括孔隙个数、直径、方向角、面积、周长、外接椭圆的长轴和短轴等,方便后续微观结构参数的计算。
3 微观结构图像分析
3.1 微观参数的计算
使用Matlab编写算法提取微观结构参数,主要用到的定量参数的含义及算法如下。
(1)灰度熵Df
一张灰度图像可看作一种离散信源,使用熵来描述图像的信息量[19]。图像的灰度熵定义为:
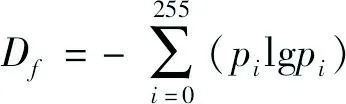
(2)
式中:pi——第i级灰度出现的频率。
图像的灰度熵可以有效表征图像灰度分布的均匀与离散情况。当土样表面具有较多裂隙时,图像灰度的分布较为分散,灰度熵较大;裂隙较少或没有充分发育时,图像灰度较为集中,灰度熵较小。
(2)平均孔径D
孔径是描述孔隙大小最基本的特征。在对SEM图像的结构进行分析时,孔径被定义为孔隙边缘轮廓的最长弦[13]。所有孔隙的孔径平均值为平均孔径。平均孔径越大,土体的孔隙越大。
(3)扁圆度R0和形状系数F
扁圆度和形状系数是描述孔隙形状的参数。用扁圆度R0来描述孔隙形状接近圆形的程度,指的是孔隙外接椭圆的短轴与长轴之比。扁圆度取值范围为[0,1],扁圆度越小孔隙越狭长,扁圆度越大孔隙越接近圆形。形状系数F指孔隙的实际周长与孔隙等面积的圆周长的比值,形状系数大表示孔隙轮廓的复杂度大,孔隙表面起伏大,形状系数小则反之。
(4)分布分维Dpd
图像的孔隙分布既反映孔隙形态,又可说明土体的密实状况。分形维数值越大,土中孔隙分布越复杂。采用盒计数法计算分布分形维数:
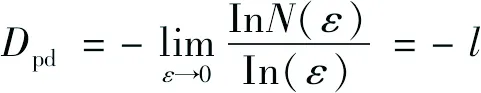
(3)
式中:ε——正方形盒子边长;
N(ε)——网格中含有孔隙的总格子数;
l——线性部分斜率。
(5)概率熵H
概率熵H引自现代信息系统理论[20],是[0,1]之间的值,H越小,表示土结构单元体排列混乱度越小,当在某一方向完全定向时,H=0;当要素排列完全随机时,H=1。概率熵的计算方法如下:
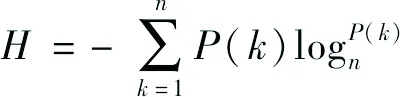
(4)
式中:P(k)——第k个方向区间的孔隙分布概率值。
在本次研究中,n=18,即0 °~180 °范围中分为18个区间,k=1表示介于0 °~10 °之间,P(1)表示孔隙方向角在0 °~10 °的分布概率值。
3.2 微观参数分析
为了对比不同渗透系数的红土微观结构定量参数,所有土样均选取放大倍数为3 000倍的SEM图像进行微观结构定量分析。由于每个土样均拍摄了多张SEM图片,因此使用同一土样多张SEM图片计算微观定量参数的平均值。表2为各土样微观结构定量参数计算的结果。从表中可以看出,不同渗透系数的土样,与孔隙的平均孔径、形状系数、分布分维、概率熵等微观结构参数之间具有一定的变化规律。

表2 N2红土微观结构定量分析结果Table 2 Microstructure quantitative analyses of N2 laterite
(1)灰度熵
各土样灰度熵变化不大,在0.88~0.92之间波动,说明红土孔隙发育较为充分,各土样孔隙的灰度分布和离散程度均匀,纹理特征相似。
(2)孔隙的大小
不同渗透系数土样的平均孔径如图5所示,从图中可以看出,红土的平均孔径在2.7~3.7 μm之间,且与渗透系数之间呈指数关系,随着平均孔径的增大,渗透系数也增大,且增长速率逐渐变大。

图5 平均孔径与渗透系数的关系曲线Fig.5 Relationship between the average aperture and permeability coefficient
根据雷祥义[21]对孔隙的分类标准,将各个土样的孔隙按半径大小分为微孔隙(<1 μm)、小孔隙(1~4 μm)、中孔隙(4~16 μm)和大孔隙(>16 μm)四类。选取渗透系数相差较大的5组土样进行对比,统计结果如图6所示。从图6(a)中可以看出,小孔隙数量占所有孔隙的45%~65%,是红土孔隙的重要组成部分。微孔隙和中孔隙所占比例次之,均为20%左右,大孔隙的数量最少。随着土样的小孔隙数量减少,中孔隙和大孔隙数量增加,渗透系数也随之增加。由图6(b)可知,中孔隙和大孔隙的面积约占总面积的80%以上,红土的孔隙面积主要由中孔隙和大孔隙决定。随着小孔隙的面积减小,中孔隙和大孔隙面积增大,渗透系数有所增加。
(3)孔隙的几何形态
孔隙的几何形态使用扁圆度和形状系数来形容。由图7所示,红土中孔隙的扁圆度在0.54~0.57之间,扁圆度和渗透系数呈指数关系,随着扁圆度的增加,渗透系数减小。组成红土的颗粒在平面上相互交错排列组成的孔隙结构稳定,孔隙的形状系数在0.63~0.75之间,随着形状系数的增大,渗透系数呈线性减小。这是由于红土中黏粒含量较多,黏粒的分布造成了孔隙轮廓的起伏,黏粒含量多的红土,孔隙轮廓起伏较大,形状系数较大,黏粒增多导致渗透系数减小。
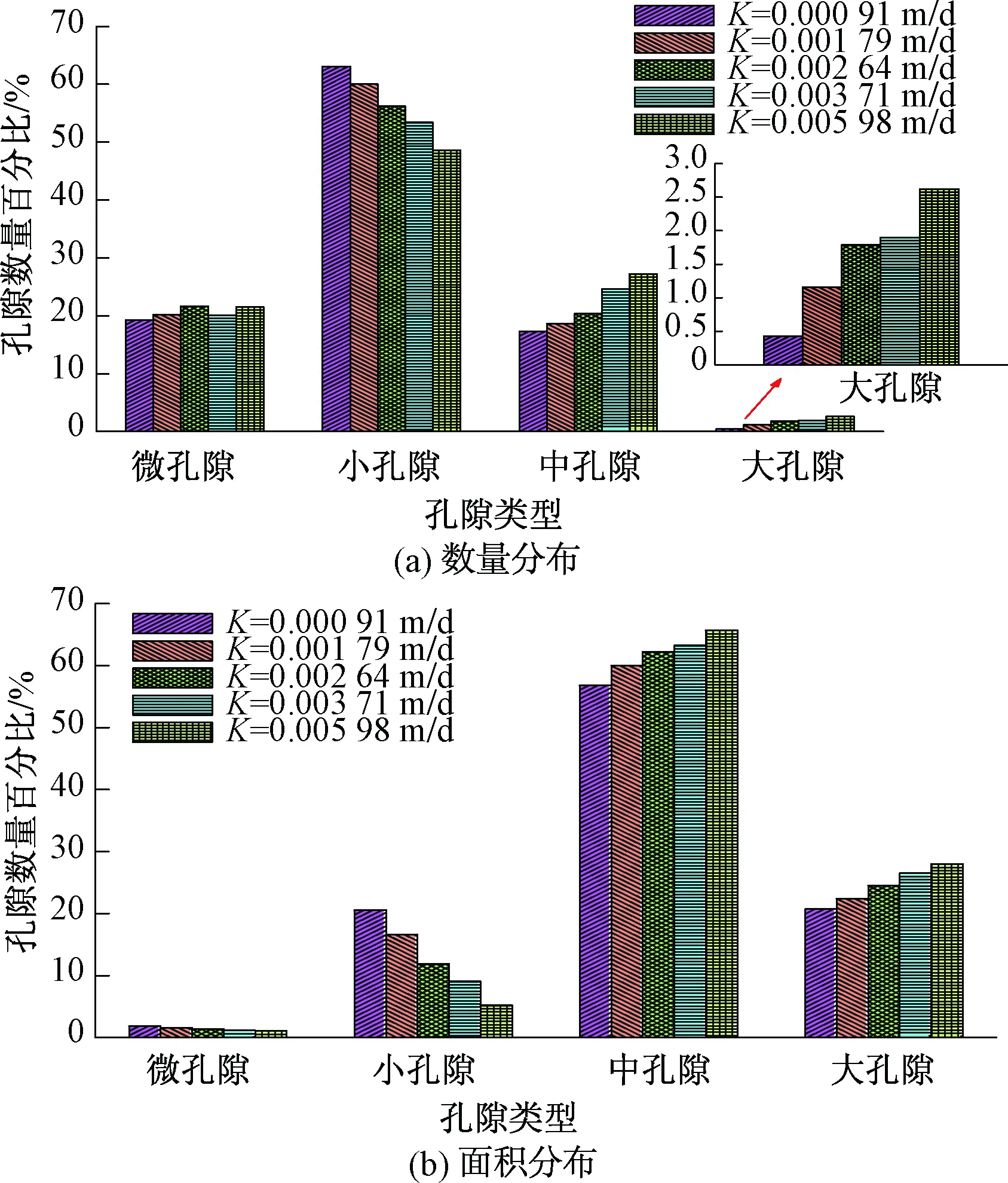
图6 孔隙数量、面积分布直方图Fig.6 Histogram of the pore number and area distribution
(4)孔隙的平面分布分维
孔隙的平面分布具有分维特征(图8)。红土中孔隙的分维数在1.00~1.40之间,分布分维与渗透系数之间呈衰减型指数关系,孔隙分布分维较大的土样,孔隙分布情况复杂,孔隙较为分散,不利于水的通过,渗透系数小。随着分布分维的增大,土体中的孔隙逐渐由大变小,且减小的速率越来越慢。渗透系数随之减小。
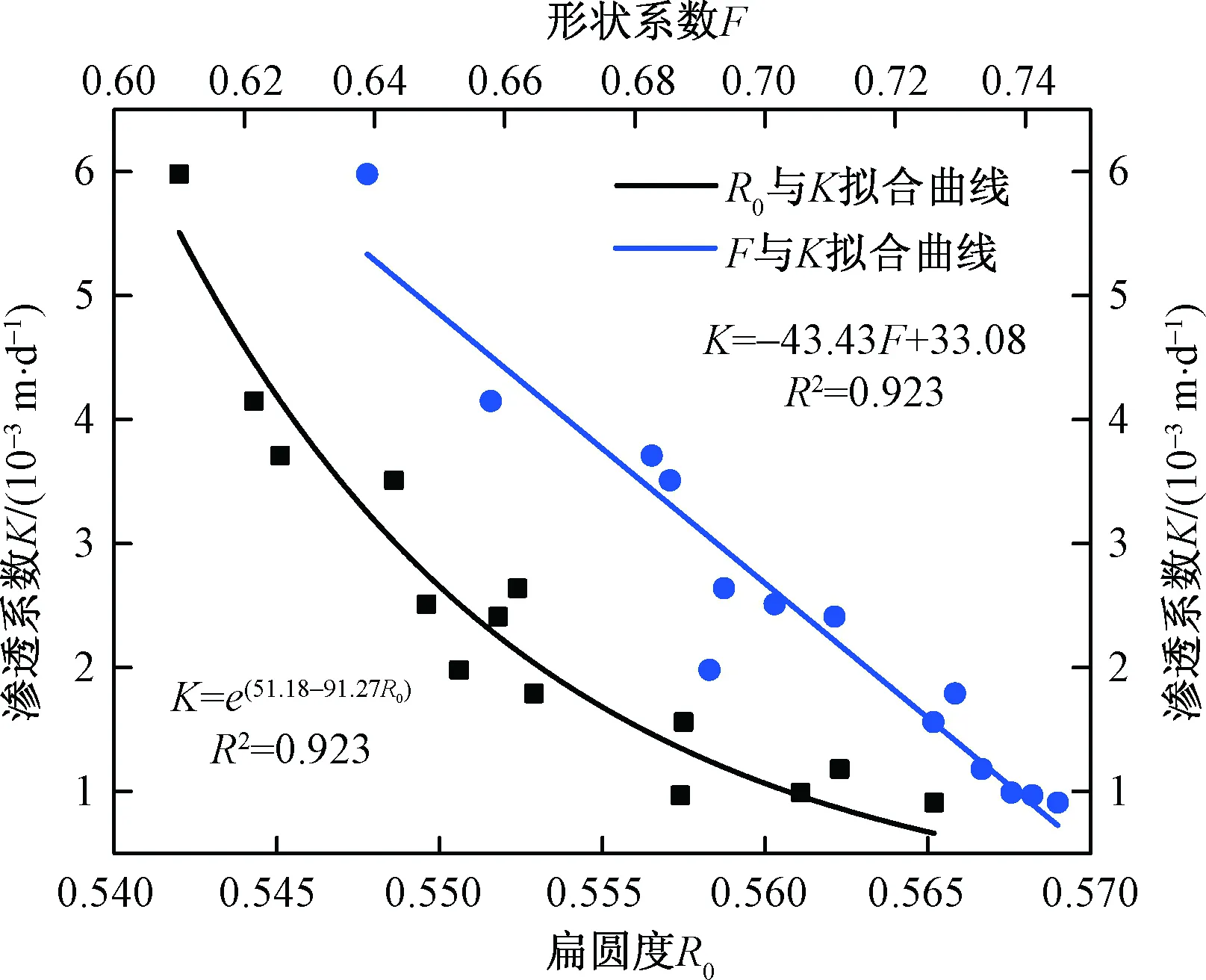
图7 扁圆度、形状系数与渗透系数的关系曲线Fig.7 Relationship between the oblateness, shape coefficient and coefficient of permeability
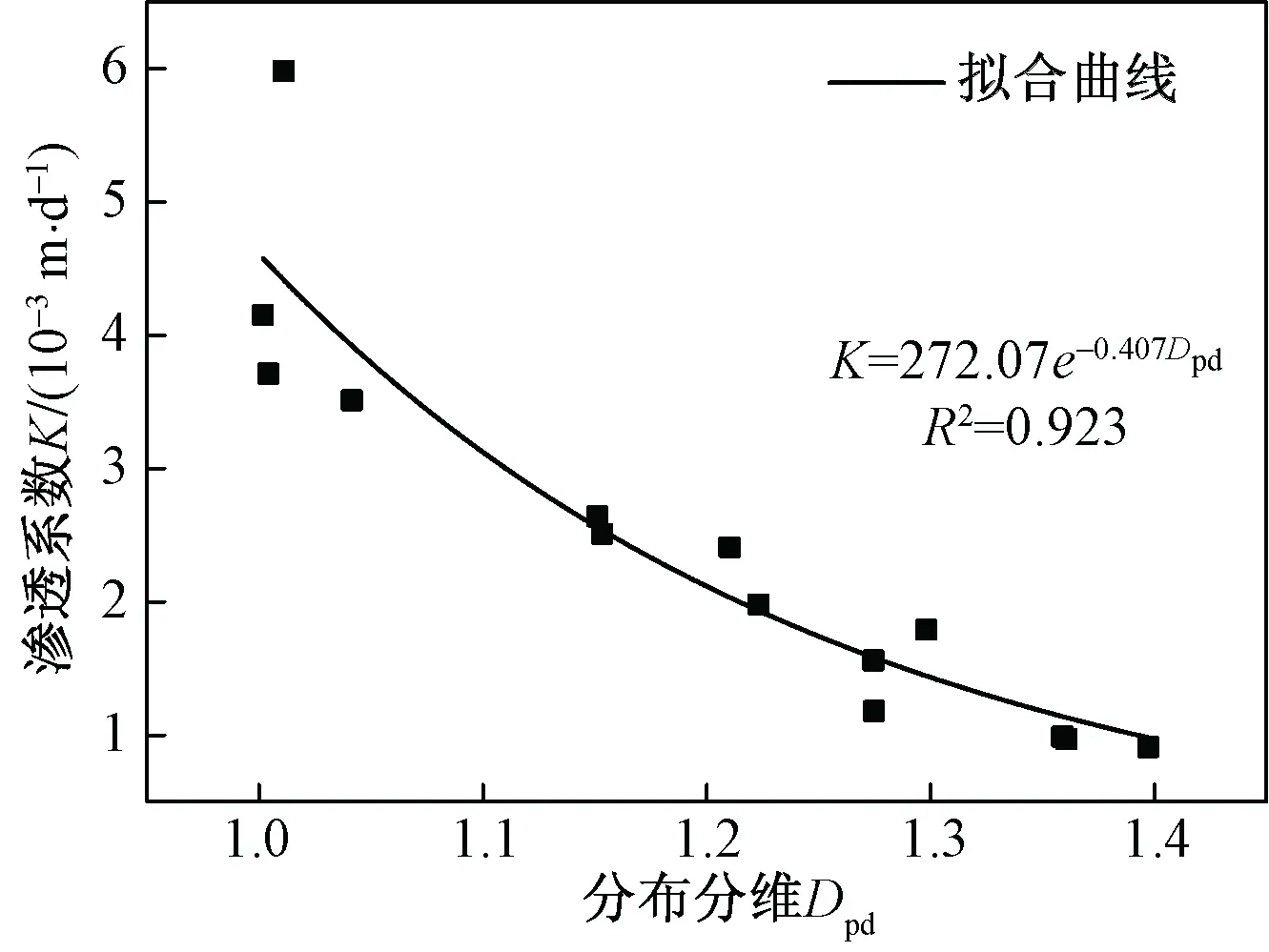
图8 分布分维与渗透系数的关系曲线Fig.8 Relationship between the fractal dimension of distribution and permeability coefficient
(5)孔隙的排列情况
如表2所示,孔隙的概率熵在0.97~0.99之间,孔隙在空间上的排列处于混乱、无序的状态。
将孔隙分布的角度按10 °为一个区间,把180 °等分为18个方位区间,统计每个区间内孔隙的累计面积,以各区间内孔隙面积与图像所有孔隙总面积的比值为数据绘制玫瑰花图,选取其中三个土样进行观察,结果如图9所示。各土样的玫瑰花图均存在“尖锐”的特点,表现出较差的定向性,各区间分布差异大。
4 结论
(1)微观结构分析表明,西北地区N2红土的小孔隙数量最多,约50%以上,中孔隙占红土孔隙面积最大,约60%以上;随着小孔隙数量和面积减小,中孔隙及大孔隙数量和面积的增大,渗透系数增大。
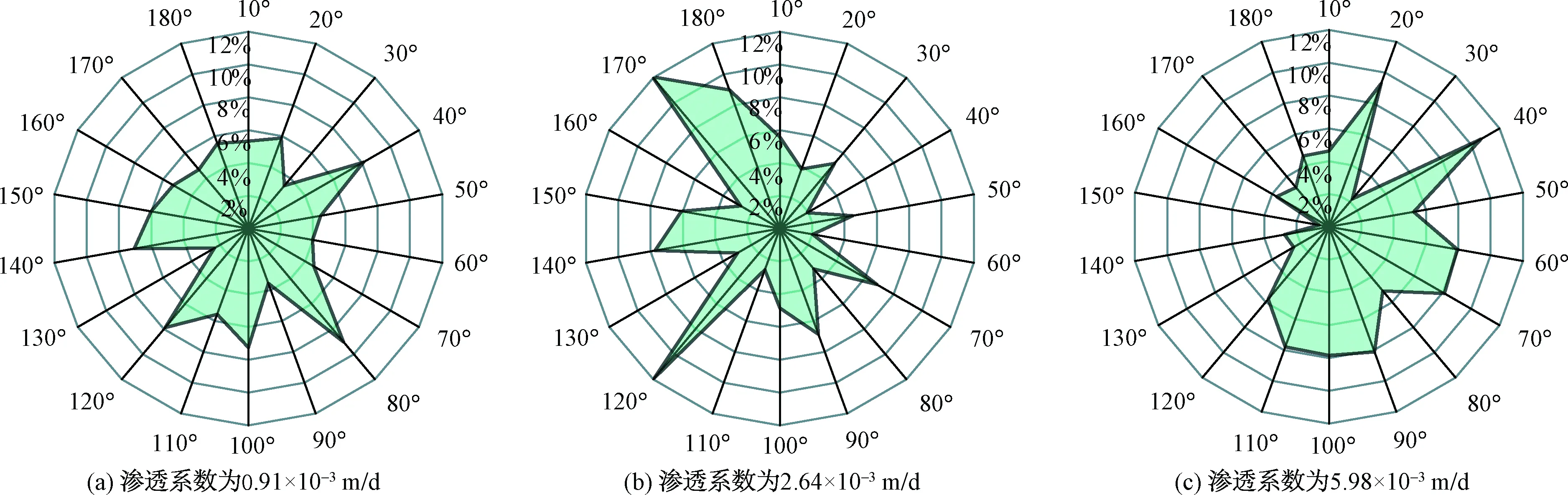
图9 不同渗透系数的红土孔隙分布玫瑰花图Fig.9 Pore distribution rose diagrams of laterite with different permeability coefficient
(2)灰度熵与渗透系数大小无明显关系,孔隙分布的离散情况相似;渗透系数随平均孔径的增大呈指数型增长,平均孔径越大,渗透系数越大。
(3)红土中的孔隙主要呈不规则椭圆状,渗透系数随扁圆度的增大呈指数型缓慢减小;渗透系数随形状系数的增大呈线性减小,孔隙轮廓起伏逐渐变小,变得更加光滑。
(4)渗透系数随孔隙的分布分维呈指数型减小,随着分布分维的增加,孔隙分布由集中变得相对分散,孔隙由大孔隙逐渐变为小孔隙,渗透系数随之减小;概率熵与渗透系数之间无明显变化关系,孔隙方向玫瑰花图中各方向区间内的孔隙分布不均匀,说明孔隙的定向性差。
