跨越饱和/非饱和土壤条件下竖直地埋管换热器传热特性研究

2020-04-15蔡学龙王松庆

可再生能源 2020年4期

蔡学龙，王松庆

（东北林业大学土木工程学院，黑龙江哈尔滨 150040）

0 引言

受到占地面积和换热稳定性等因素的限制，土壤源热泵系统的室外地下换热器多采用竖直地埋管换热器（以下简称为地埋管）。地埋管通常会跨越不同的地质层，即一部分位于无渗流区，另一部分位于地下水位以下。对于前者，地埋管与周围土壤之间的传热过程是一个温度梯度下的热量传递和土、水势梯度下的水分迁移相互耦合的复杂传热传质过程；对于后者，地埋管与周围土壤之间的传热过程是一个温度梯度下的热传导和水力梯度下的对流换热相互耦合的传热过程。对于实际工程中的地埋管，如果将其与土壤之间的传热过程等效为纯导热问题，并单纯地选用线热源模型或柱热源模型等进行分析和设计，会造成设计结果与实际结果偏差较大，影响土壤源热泵系统的运行性能及其初期投资[1]，[2]。

地埋管的换热性能不仅与其周围土壤的物性参数密切相关，还会受到地下水渗流和分层作用的影响[3]。 Chiasson[4]通过有限差分法，分析了地下水渗流对地埋管换热性能的影响，分析结果表明，若忽略地下水在土壤中的迁移，会导致地埋管几何尺寸设计得偏大，使得初期投资随之增加。 Angelotti[5]研究了地下水渗流速度对土壤传热性能以及热干扰的影响，分析结果表明，地下水渗流速度越大，地埋管周围土壤的等温线沿渗流方向的偏移度越大。 Capozza[6]研究了地下水渗流对于土壤中热量迁移情况的影响，分析结果表明，若考虑地下水渗流，则会导致地埋管总长度的预测值减小。

实际情况下，土壤的分层情况以及物性的不均匀情况均会对地埋管换热器的传热情况产生影响，但影响规律尚不明确，值得深入探讨[7]。景政[8]通过数值方法和实验方法，研究了渗流作用对地埋管传热情况的影响，分析结果表明，渗流作用会大幅度地增加土壤的导热系数以及地埋管与周围土壤之间的换热量。张琳琳[9]建立了同时考虑分层和渗流作用的地埋管传热解析模型，模拟结果表明，部分土壤层存在渗流时的热作用距离比全部土壤层存在渗流时的热作用距离减小了43%。可见，地下水渗流和分层作用对地埋管传热性能的影响是不容忽视的。

上述研究虽然考虑了渗流作用和分层作用，但没有考虑渗流作用情况下，非饱和土壤和饱和土壤相邻间隔分层布置时，地埋管的传热特性。本文同时考虑分层作用和渗流作用，并采用数值仿真方法研究了地埋管跨越非饱和土壤和饱和土壤时的传热规律，为土壤源热泵系统的设计提供理论依据。

1 控制方程

1.1 地埋管换热器传热模型

由于地埋管换热器内循环液（工质）的流线会在U 型管的弯管处发生较大的变化，因此本文采用Realizable k-ε 模型描述地埋管换热器内循环液的流动和传热情况。

地埋管换热器内循环液的连续性方程为

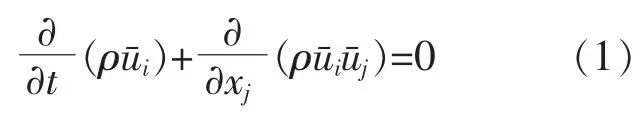
式中：ρ 为地埋管换热器内循环液的密度，kg/m3；分别为地埋管换热器内循环液在 x 轴、y 轴方向上的流速，m/s；xj为y 轴方向上地埋管换热器内循环液的流动距离，m。

地埋管换热器内循环液的动量方程为[10]

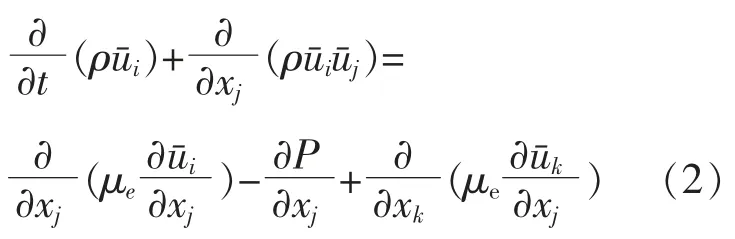
式中：μe为地埋管内循环液分子扩散造成的动力粘性；xk为z 轴方向上地埋管换热器内循环液的流动距离，m；为地埋管换热器内循环液在z 轴方向上的流速，m/s。

地埋管换热器内循环液的能量方程为

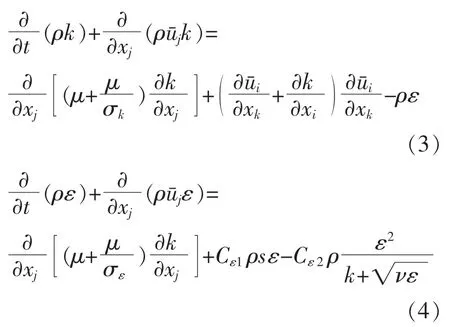
式中：xi为x 轴方向上地埋管换热器内循环液流动的距离，m；k 为地埋管内循环液的湍流脉动动能，J；μt为地埋管换热器内循环液的湍流粘性系数；μ 为地埋管换热器内循环液的动力粘度，（N·s）/m2；ε 为地埋管换热器的效能；ν 为地埋管换热器内循环液分子的粘性；Cε1，Cε2均为系数，Cε1=1.2，Cε2=1.44；σk，σε均为常量，σk=1.0，σε=1.2[11]。

1.2 土壤传热模型

1.2.1 饱和土壤传热模型

对于有、无渗流的饱和土壤，一个物质系统或空间体积内含有固体和液体2 个部分。因此，对于选取的任意一个控制体积而言，令其孔隙率为φ，那么单位体积内液体和固体骨架占据的体积分数分别为 φ 和1-φ ，于是本文基于体积平均法，构建出多孔介质中各部分的能量方程[12]。

多孔介质中液体相的能量方程为

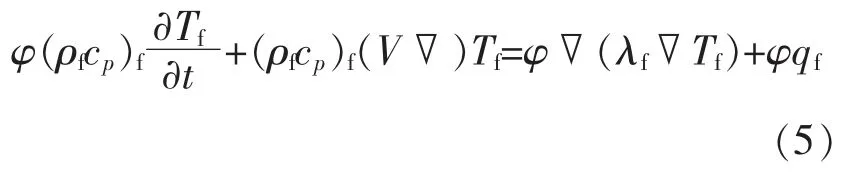
式中：ρf为多孔介质中液体相的密度，Kg/m3；cp为多孔介质中液体相的定压比热，J/（Kg﹒℃）；Tf为多孔介质中液体相的温度，℃；λf为多孔介质中液体相的导热系数，W·（m·℃）-1；V 为土壤的体积，m3；qf为多孔介质中单位体积液体相的内热源产生的热量，J/m3。

多孔介质中固体相的能量方程为

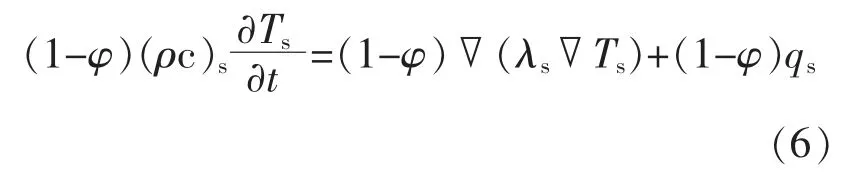
式中：ρ 为土壤的干密度，kg·m-3；c 为土壤的比热，J/（kg·℃）；Ts为土壤的温度，℃；λs为多孔介质中固体骨架的导热系数，W/（m·℃）；qs为多孔介质中单位体积固体骨架相的内热源产生的热量，J/m3。

通常可以假设流体和固体可以在瞬间达到局部热平衡状态，此外，本文将流体、固体的热容和导热系数均视为常数，则基于式（5），（6）可得到有渗流的饱和土壤的能量方程为

式中：λm为土壤的表观导热系数，W/（m·℃）；T 为土壤的温度，℃；qm为土壤的表观内热源产生率；cm为土壤的表观容积比热，J/（kg·℃）。

式（7）中 ρcm，λm，qm的计算式分别为

1.2.2 非饱和土壤传热模型

在土壤非饱和区，非等温条件下，土壤水分的迁移可以由扩散达西定律进行描述[13]。其中：液相质流由对流质流和表面扩散质流组成；蒸汽质流由蒸汽对流质流和蒸汽在多孔介质中产生的扩散质流组成；空气质流由对流质流和扩散质流组成。

液相、蒸汽和空气的质流方程分别为

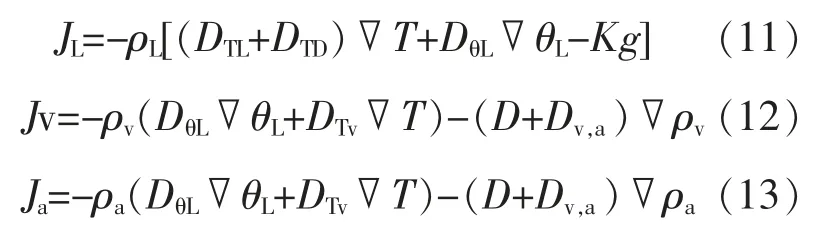
式中：JL，Jv，Ja分别为液态水、蒸汽、空气的质流，kg/s；DTL为水的热质扩散系数；DTD为吸附传递系数；D 为分子扩散系数；DθL为等温质扩散系数；DTv为蒸汽热质扩散系数；Dv，a为 Knudsen 扩散系数；θL为液相的百分比；K 为水力传导系数；g 为重力加速度，N/kg；ρL为液态水的密度，kg/m3； ρv为蒸汽的密度，kg/m3；ρa为空气的密度，kg/m3。

土壤非饱和区的质量守恒方程为

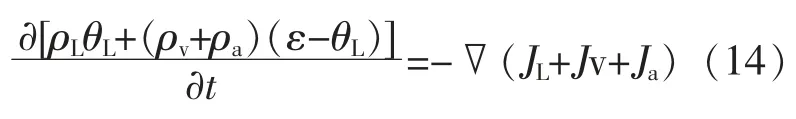
土壤非饱和区的能量守恒方程为

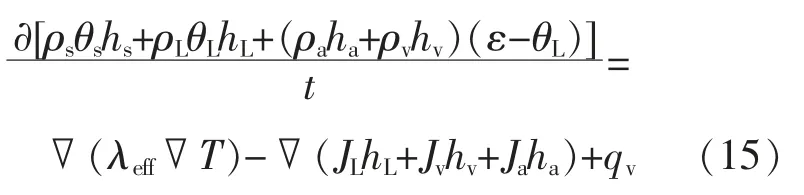
式中：ε 为土壤的孔隙率；hL，hv，ha分别为液体、蒸汽、空气的焓值；qv为土壤内热源；λeff当量导热系数，W/（m·℃）。

λeff的计算式为

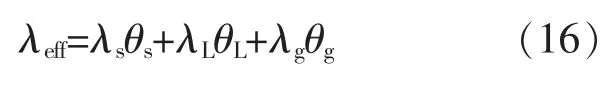
式中：θs，θL，θg分别为固相、液相和气相的百分比。

θs，θL，θg的关系式为

2 数值仿真研究

2.1 物理模型建立与网格划分

本文采用相似理论建立几何尺寸小于实际情况的物理模型。在考虑分层和渗流同时作用的情况下，若按照实际几何尺寸设计模型，则会导致在仿真过程中难以控制水在分层土壤中渗流的均匀性，仿真计算也很难收敛。利用几何尺寸小于实际情况的物理模型能规避上述问题。

本文的模型为长方体，几何尺寸为800 mm×800 mm×900 mm。利用3 个等分点将该模型上表面的一条对角线等分成4 份，以该对角线中点两侧的等分点为中心，向下布置了两根U 型管，每根U 型管的内径均为8 mm，外径均为10 mm，长均为830 mm，U 型管两支管的管心距均为 40 mm。由于U 型管与土壤之间的接触面存在复杂性，因此，该模型采用非结构化网格进行划分，并将U 型管管壁设置为边界层，此外，对于U 型管由内到外适当地增大网格的尺寸，以减少网格数量，提高计算效率。

为了确保计算结果的准确性，须定量地确定模型的最优网格数，因此，本文进行了网格的无关性分析。考虑模拟过程中的各种约束条件，分别计算了4 种不同的网格划分模型，网格数量分别为700 000，900 000，1 100 000 和 1 400 000，网格质量均为 0.5～1。监测的温度：U 型管壁面的最高温度、平均温度，以及U 型管出口工质的平均温度。

每种工况各处监测温度以及各工况之间相对误差的具体情况如表1 所示。表1 中的相对误差为相邻工况测量结果之间的偏差。

表1 网格独立性验证Table 1 Verification of grid independence

由表1 可以看出，当网格数量不低于110 万时，各项测量结果大体上保持不变，相对误差均小于0.1%。因此，本文采用的网格数量为110 万，这样既能够保证计算精度，又能够保证计算效率。

2.2 仿真参数与测点设置

2.2.1 砂土热物性参数

本文对砂土进行水平分层布置，自下而上分别为饱和砾砂层、非饱和中砂层和饱和粗砂层，厚度均为300 mm。由于中砂的保水性优于砾砂和粗砂，故将中砂设置成非饱和砂土，这样会使得非饱和土壤层的含水率更加均衡。

各层砂土的热物性参数如表2 所示。

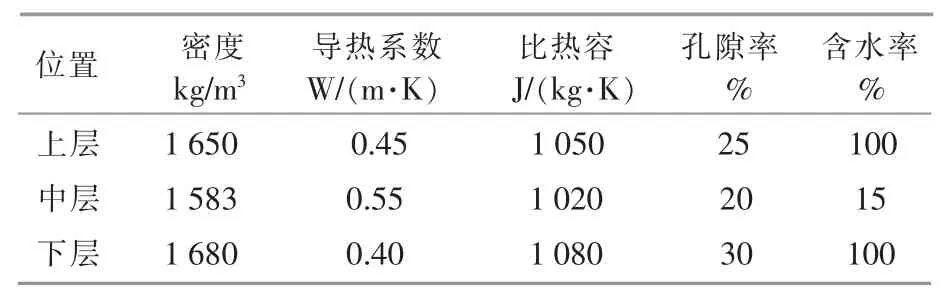
表2 各层砂土的热物性参数Table 2 Thermophysical parameters of each layer of sand

2.2.2 边界条件设置

模型的各个壁面均设置为绝热壁面，U 型管入口、出口和土壤渗流入口、出口均设置为速度入口、出口。U 型管壁面及其与土壤层之间的交界面均设置为耦合传热。此外，设置模型中的工质为多孔介质混合流，由于土壤中渗流速度较低，因此，该混合流也被视为线性流。U 型管的材质为铜，其内部的工质为水。本文研究了2 种工况下，土壤温度的变化特性。这2 种工况均为夏季工况。各工况下，模型的仿真参数如表3 所示。

表3 2 种工况下，模型的仿真参数Table 3 Simulation parameters of the model under 2 working conditions

2.2.3 测点设置

图1 为土壤中各测点的布置情况。

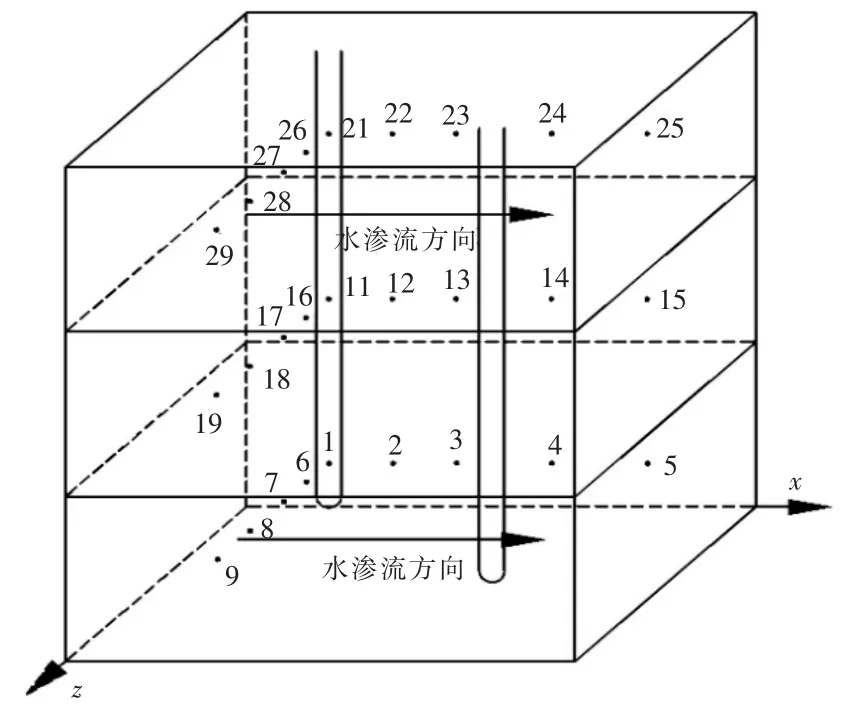
图1 土壤中各测点的布置情况Fig.1 Arrangement of measuring points in soil

由图1 可知，在每个土壤层的x 轴、z 轴方向上各布置了 5 个测点。对于下土壤层，测点 1，2，3以及测点 1，6，7 的间距均为 100 mm；测点 3，4，5以及测点7，8，9 的间距均为150 mm；其他土壤层中各测点的布置方式与下土壤层相同。

2.3 案例分析

2.3.1 无渗流条件下土壤温度变化特性研究

地埋管中的热量会向土壤的四周传递，传递情况和传递规律将对该地埋管的设计有重要影响。当土壤层中无渗流（工况1）时，中土壤层、下土壤层中各测点处的温度随时间的变化情况如图2 所示。

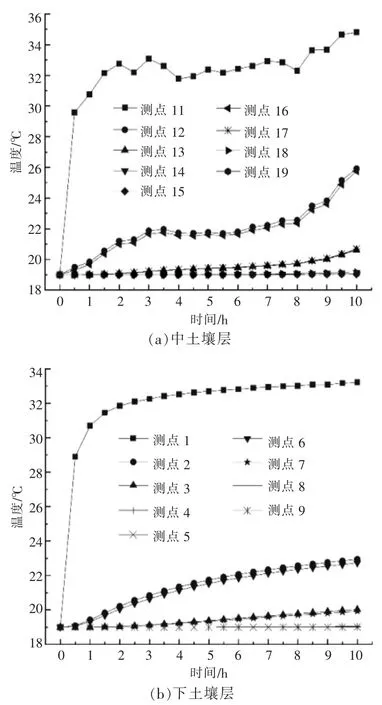
图2 当土壤层中无渗流时，中土壤层、下土壤层中各测点处的温度随时间的变化情况Fig.2 When there is no seepage in the soil layer，the temperature changes with time at each measuring point in the middle soil layer and the lower soil layer

由图2 可知，在下土壤层x 轴、z 轴两个方向上，均是靠近U 型管测点处的温度升高速率较快，远离U 型管测点处的温度升高速率较慢，且两个方向上离U 型管等距离测点处温度的升高幅度大致相等。其中，测点12 与测点16 的温度变化曲线几乎重合，x 轴、z 轴方向上其他对应测点温度的变化情况也大致相同，这说明在该土壤层中x 轴、z 轴方向上的传热情况相同，因此，在无渗流情况下，分析土壤层x 轴方向上的传热情况可以确定土壤层z 轴方向上的传热情况。此外，通过研究发现，各土壤层中各测点处温度的变化趋势相同。

为了更全面地明确各测点处土壤温度的变化规律，对工况1 下各土壤层中各测点的温度变化特性进行深入分析。由图2 可知，下土壤层各测点处的温度均呈现出逐渐升高的变化趋势，这说明热源传递至各测点处的热量始终大于各测点处向外传递的热量（上土壤层也有相似的传热特性）。中土壤层的传热情况不同于下土壤层，虽然该土壤层各测点处的温度也呈现出逐渐升高的变化趋势，但在温度升高的过程中，各测点处的温度出现波动现象，温度上升趋势不稳定，这说明热源传递到各测点的热量有时大于各测点处向外传递的热量，有时小于各测点处向外传递的热量。这是由于非饱和砂土中的水分在地埋管运行过程中会向温度高的区域移动，水分的迁移会造成砂土中各区域的含水率随时间发生变化，此外，砂土的导热系数与砂土含水率有关，当含水率发生变化时，会引起砂土的导热系数随之发生变化[14]。综上可知，饱和土壤中的热流量比非饱和土壤中的热流量更稳定。

当土壤层中无渗流，运行时间为10 h 时，各土壤层x 轴方向上各测点处的温度相对于初始温度的升高幅度，如表4 所示。

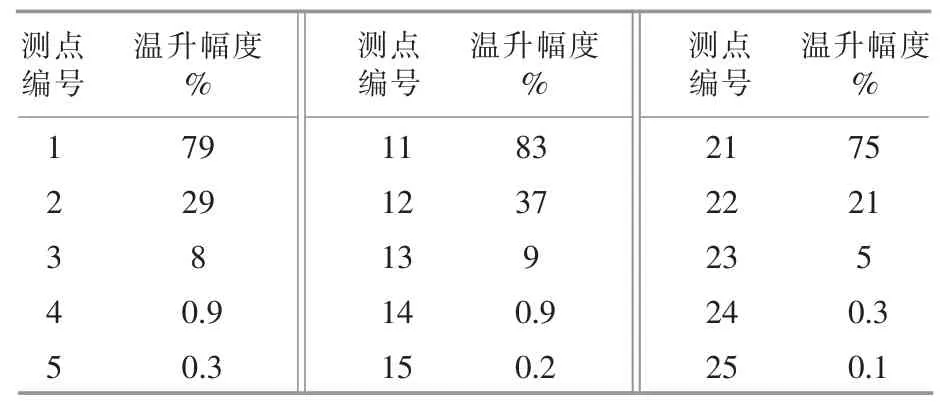
表4 当土壤层中无渗流，运行时间为10 h 时，各土壤层x 轴方向上各测点处的温度相对于初始温度的升高幅度Table 4 When there is no seepage in the soil layer and the operation time is 10 hours，the temperature of each measuring point in the x direction of each soil layer increases with respect to the initial temperature

由表4 可知，对于不同的土壤层，距离U 型管中心越远，其温度相对于初始温度的升高幅度越小，这是由于距离U 型管越远，相邻砂土之间的温度差越小，传热量也越小。因此，土壤中的热流量与其和U 型管中心之间的径向距离成反比关系。

2.3.2 渗流条件下土壤温度变化特性研究

当土壤中有渗流时，中土壤层、下土壤层中各测点处的温度随时间的变化情况如图3 所示。

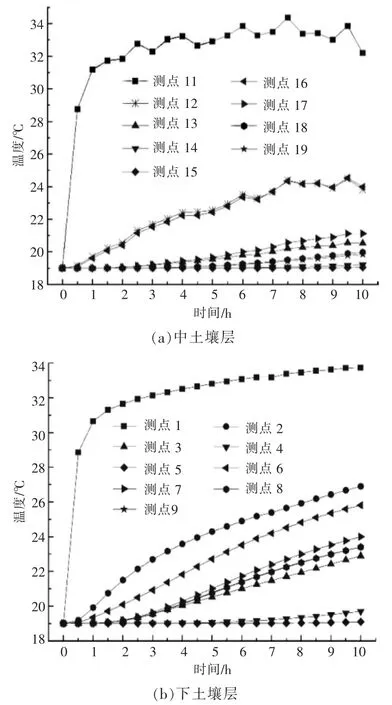
图3 当土壤中有渗流时，中土壤层、下土壤层中各测点处的温度随时间的变化情况Fig.3 When there is seepage in the soil，the temperature changes with time at each measuring point in the middle soil layer and the lower soil layer

由图3 可知，当土壤中有渗流时，下土壤层x轴方向上测点2～5 和z 轴方向上测点6～9 的温度变化情况存在较大差异，这表明对于存在渗流的下土壤层，其内部x 轴、z 轴方向上有着不同传热的特性。此外，经过研究发现，上土壤层也有类似传热特性。由图3 还可看出，当土壤中有渗流时，中土壤层x 轴方向上测点12～15 和z 轴方向上测点16～19 的温度变化情况相似，这表明对于存在渗流的中土壤层，其x 轴、z 轴方向上有着相同的传热特性，综上可知，当饱和土壤层中有渗流时，其x 轴、z 轴方向上有不同的传热特性，对于非饱和土壤层以及没有渗流的饱和土壤层，x 轴、z 轴方向上的传热特性相同。

工况 1，2 下，上土壤层 x 轴、z 轴方向上各测点处的温度随时间的变化情况分别如图4，5 所示。

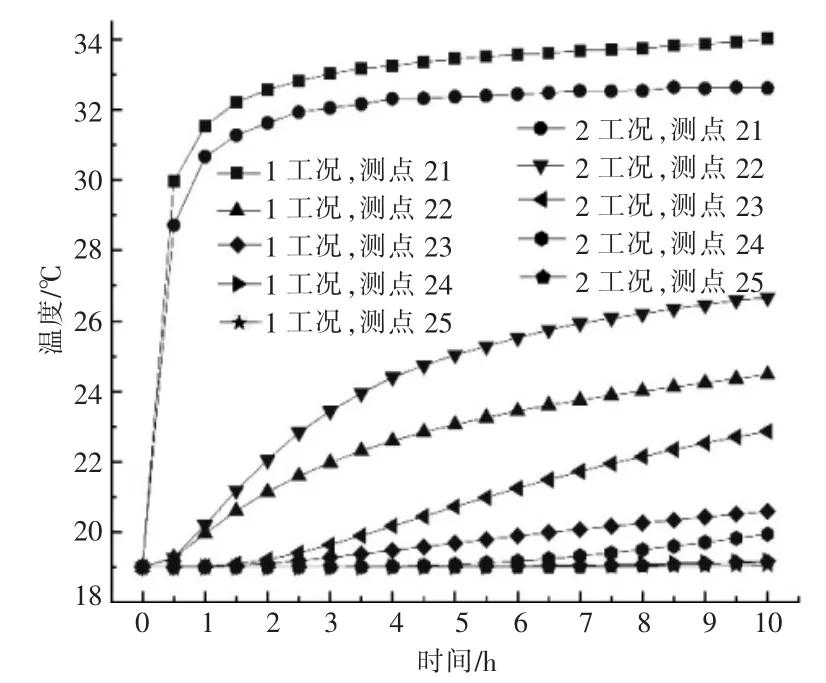
图4 工况1，2 下，上土壤层x 方向上各测点处的温度随时间的变化情况Fig.4 Under working condition 1 and 2，the change of temperature with time at each measuring point in x direction of upper soil layer

图5 工况1，2 下，上土壤层z 方向上各测点处温度随时间的变化情况Fig.5 Under working condition 1 and 2，the change of temperature with time at each measuring point in z direction of upper soil layer

由图4，5 可知，两种工况下，测点 22，23 处的温度与初始温度之间的差值会随着运行时间的增加而增大。当运行时间为10 h 时，工况1，2 下，测点22 处的温度比初始温度分别升高了28.8%，40.3%，两者相差11.5%；由于上土壤层各测点处温度的上升曲线无交点，且变化趋势稳定，故本文在运行时间为10 h 的条件下，分析上土壤层的径向传热特性。

当运行时间为10 h 时，两种工况下，上土壤层各测点处的温度相对于初始温度的升高幅度，以及不同工况下升高幅度的差值如表5 所示。表中：ΔT1，ΔT2分别为工况 1，2 下上土壤层各测点处的温度相对于初始温度的升高幅度；ΔT 为ΔT1与ΔT2的差值，表征了土壤层的传热能力。

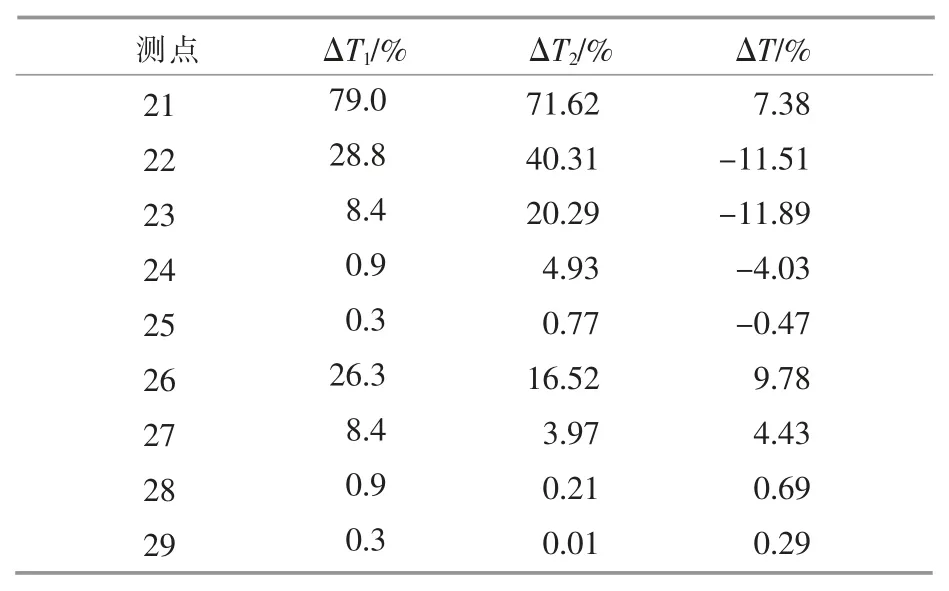
表5 当运行时间为10 h 时，两种工况下，上土壤层各测点处的温度相对于初始温度的升高幅度，以及不同工况下升高幅度的差值Table 5 When the operation time is 10 hours，the increase range of the temperature at each measuring point of the upper soil layer relative to the initial temperature and the difference of the increase range under different working conditions

由表5 可知，工况2 下，上土壤层x 轴方向上各测点处的温度始终高于工况1 下各测点处的温度；上土壤层z 轴方向上大部分测点处的温度始终高于工况1 下各测点处的温度（测点21 除外），这说明当土壤中存在渗流作用时，渗流方向上土壤的传热能力被强化，垂直渗流方向上土壤的传热能力被弱化。通过计算得到，渗流方向上ΔT 的平均值约为7%，垂直渗流方向上ΔT 的平均值约为-3.8%，这是由于渗流作用能够加速渗流方向上的工质的热量传导速率，从而使更多的热量向渗流方向扩散，导致垂直渗流方向上热量传递得较少。