电力市场环境下储能电站和光伏电站合作博弈模型

2020-04-15格日勒图张立辉柴剑雪

可再生能源 2020年4期

格日勒图，张立辉，柴剑雪

（1.华北电力大学经济与管理学院，北京 102206； 2.华北电力大学新能源电力与低碳发展研究北京市重点实验室，北京 102206； 3.内蒙古电力（集团）有限责任公司，内蒙古呼和浩特 010080）

0 引言

随着储能技术的发展，储能电站已成为电力系统调峰填谷、提高系统稳定性、实现需求侧管理的一种有效手段[1]，[2]。光伏发电是一种重要的新能源发电形式，大规模光伏电站的并网运行是未来发展的趋势[3]，[4]。随着电力市场规则的不断完善，储能电站和光伏电站作为决策主体参与电力市场已成为一种重要趋势。

针对多主体参与的电力市场，采用博弈论建立其运行模型是重要研究方向。文献[5]建立了考虑风电与储能参与的电力市场联动博弈模型。文献[6]针对负荷不确定性与随机线路的故障停运，建立了考虑系统运行不确定性的电力市场线性供给函数均衡模型。大部分文献研究的博弈模型所针对的都是发电侧竞价[7]，[8]。文献[9]建立的多主体博弈模型针对用电侧开放的情景。除了传统的电力市场主体，有的文献研究了微电网作为市场主体参与下的博弈模型[10]。目前，大部分文献研究的电力市场博弈模型都是非合作博弈，而且针对发电商的文献较多。尽管一些文献针对分布式电源参与电力市场博弈，但还很少针对储能电站和光伏电站组成联盟进行合作博弈参与电力市场的建模[11]。

光伏电站出力具有随机性和波动性，且受自然条件的影响，光伏电站出力预测精度仍然较低[12]。因此，光伏电站参与日前电力市场存在先天的劣势，即容易与中标电量存在偏差。针对此偏差，电网公司一般通过收取惩罚费用来激励光伏电站采用保守的竞价策略[13]。光伏电站一般通过招标电价制参与电力市场[14]。在中长期招标电价制下，光伏电站在市场上失去了竞价能力，也就失去了进一步提升收益的空间。由于储能电站具有灵活的运行模式，因此能够以多样的运行模式充分参与电力市场。然而，由于储能容量和充放电功率限值的约束，储能电站难以进一步提高收益。如果储能电站和光伏电站组成联盟将具备提高收益的潜力。在合作博弈中，储能电站和光伏电站仍然作为独立决策者参与电力市场，但是须要遵循联盟制定的协议。通过这样的方式可以提高联盟收益，并采取合理的模型对合作博弈剩余进行分配。

本文针对含发电商、售电公司、用户、储能电站和光伏电站等代理的电力市场，建立了博弈模型。其中，计及储能电站和光伏电站组成联盟进行合作博弈。合作博弈联盟以最大化联盟收益为目标，制定联盟内部交换功率和交易电价协议；储能电站和光伏电站在遵循协议的前提下作为独立决策者参与电力市场。本文基于博弈理论得到模型的Nash 均衡，并采用Shapley 值对合作博弈剩余进行分配，并通过算例验证了模型的合理性和适用性。

1 博弈主体基本模型

本文首先建立电力市场环境中各个博弈主体的基本模型，作为建立合作博弈模型的基础。博弈主体包括储能电站代理、光伏电站代理、电网公司代理、发电商代理和用户代理。

1.1 储能电站代理

储能作为一种特殊的电气设备，既要通过充电获得电量，也要通过放电获得收益。在独立运营模式下，储能电站可以在一天的各个时段选择两种运行模式：发电商模式和用户模式。

如果储能电站t 时段运行在发电商模式下，储能参与发电侧竞价，与传统的发电商的报价策略一样，采取如式（1）所示的三段式报价策略[15]。

式中：PSB（t）为 t 时段储能电站充放电功率；P1，P2，P3为阶梯式报价中各个电量区段的报价； Qmin，Qmax为最小出力、最大出力；Q2为第 1 段最大出力；Q3为第2 段最大出力；QSB为储能中标电量。

如果储能电站t 时段运行在用户模式下，储能作为一个用户向电网公司购电，购电价格为电网公司制定的销售电价p（t）。

储能电站在运行过程中的运行成本主要来自于充放电转化及充放电深度变化对使用寿命的折损[16]。计及储能运行成本，则储能电站运行一天的收益如式（2）所示。

式中：ESB为储能电站一天的运行收益；BSB（t）为 t时段储能电站发电收益或购电成本；CSB（t）为t 时段储能电站运行成本。

式中：QSB（t）为 t 时段储能电站在发电侧（发电商模式）的中标电量或者在用户侧（用户模式）的购电电量，QSB（t）≥0 为发电商运行模式，QSB（t）＜0 为用户运行模式；q（t）为 t 时段储能电站发电侧市场出清价；u1（t），u2（t）表征储能电站在 t 时段的运行状态，u1（t），u2（t）为[0，1]之间的整数，当u1（t）=1 时，为发电商运行模式，当 u2（t）=1 时，为用户运行模式，且满足 u1（t）+u2（t）=1 对任意时段t 成立。

式中：Δt 为时段长；PSB（t）为 t 时段储能电站充放电功率，PSB（t）≥0 时，储能电站运行在发电商模式进行放电，PSB（t）＜0 时，储能电站运行在用户模式进行充电；kch为储能电站充电时的损耗成本系数；kdis为储能电站放电时的损耗成本系数。

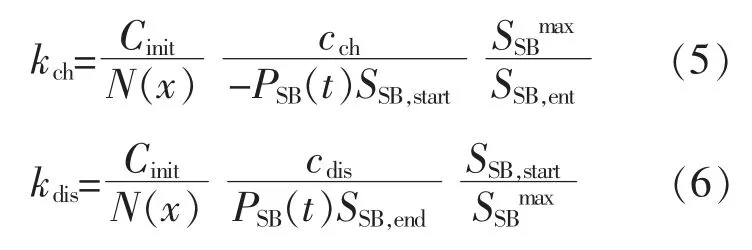
式中：N（x）为储能电池最大循环次数，由充放电深度x 决定[16]；Cinit为储能电站初始固定投资成本；SSB，start，SSB，end分别为储能电池初始、最终荷电状态；SSBmax为储能电池最高允许电量，一般为储能电池容量的0.9 倍；cch，cdis分别为充、放电影响因子。

储能电站运行须满足的约束条件包括充放电功率和剩余电量关系约束。充放电功率约束和剩余电量约束如式（7）～（9）所示。

式中：ESB（t+1）为 t+1 时段末储能电池剩余电量状态；ηch，ηdis分别为储能电池的充电效率、放电效率；DSB为储能电池自放电系数。

1.2 光伏电站代理

电网公司针对光伏电站采取招标电价制。光伏电站在中长期内参与竞标，并且就中标的电量和价格与电网公司签订中长期购电协议。由于本文所建立的模型针对的是日前市场，因此可以将光伏上网价格视作既定的常数。一方面根据招标电价制，电网公司有义务优先消纳光伏出力；另一方面，电网公司也有权利对大于投标电量的光伏出力部分不予消纳，并对小于投标电量的不足出力收取惩罚费用计于电费中。光伏电站一天的运行收益如式（10）所示。

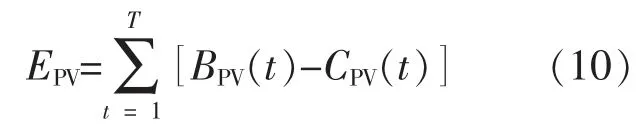
式中：EPV为光伏电站一天的运行收益：BPV（t）为光伏电站在t 时段的发电收益；CPV（t）为光伏电站在t 时段的运行收益。

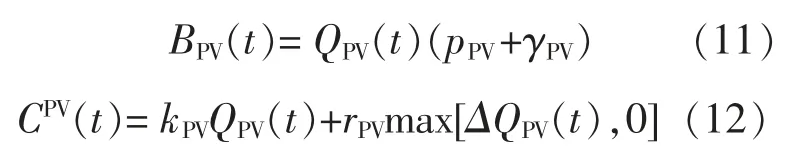
式中：QPV（t）为 t 时段光伏电站中标电量；pPV为电网公司与光伏电站签订的上网电价；γPV为政府对光伏发电的补贴价格；kPV为光伏电站运行维护成本系数；ΔQPV（t）为不平衡功率，当 ΔQPV（t）＞0 时，光伏电站实际出力小于中标出力，当ΔQPV（t）≤0 时，光伏电站实际出力大于中标出力；rPVmax[ΔQPV（t），0]为出力不足惩罚费用；rPV为惩罚系数。

1.3 其他代理

电力市场中参与博弈的主体还有电网公司代理、用户代理和其他发电商代理。目前，已有一些文献针对以上代理进行了研究，本文不再赘述。其中，对电网公司代理采取文献[17]中的模型，对用户代理采取文献[18]中的模型，对其他发电商代理采取的模型参考了文献[15]。本文的电力市场竞价机制采取统一市场出清价格（Market Clearing Price，MCP）机制，在发电侧采取竞价模式，电网公司对发电侧中标的电量采用市场出清价结算[19]。

2 合作博弈模型

2.1 合作博弈联盟

博弈模型的基本要素包括参与者、策略和支付[20]。本文的合作博弈参与者包括联盟代理（下文简称联盟）中的储能电站和光伏电站。博弈策略包括储能电站参与电力市场运行和竞价策略。储能电站与光伏电站的交易电量策略由光伏电站代理制定，交易价格由联盟制定。如果一个博弈中由决策者达成了有约束力的协议，那么该博弈就是合作博弈。本文合作博弈模型中储能电站和光伏电站的交易电量以及交易价格即为协议。与联营模式不同的是，在合作博弈模型下，储能电站和光伏电站还是独立的运营主体，仍然追求自身利益，有着各自的策略，模型中还须要解决合作剩余的分配问题。

在合作博弈模式下，储能电站和光伏电站作为新的主体参与电力市场竞价，联盟需要最大化收益，如式（13）所示。

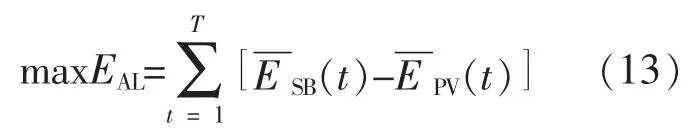
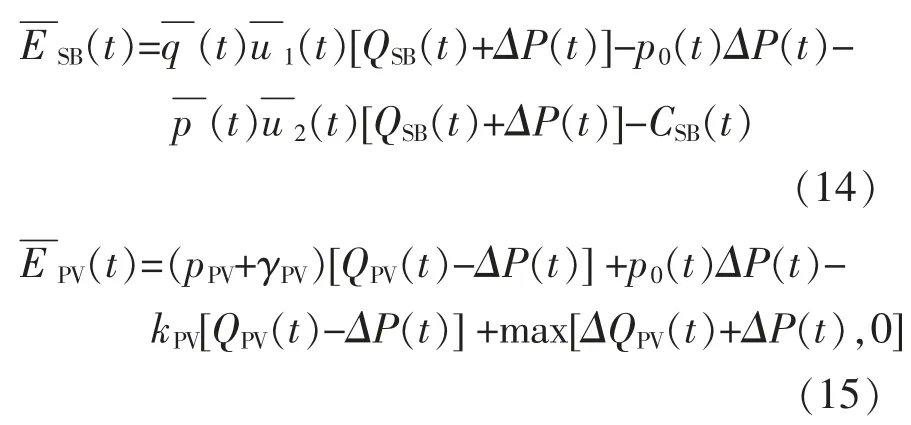
当 ΔP（t）≥0 时，表示光伏电站向储能电站输送功率，实际上更准确地理解是光伏电站代替储能电站在市场中出力；当 ΔP（t）＜0 时，表示储能电站代替光伏电站在电力市场出力，比如用于平抑不平衡功率。

在电力市场中，与储能电站和光伏电站独自参与电力市场相比，合作博弈会对出清价格和销售价格产生影响。本文根据MCP 机制进行电力市场出清，并将出清价格和销售价格看作是各博弈主体策略的函数，则有：

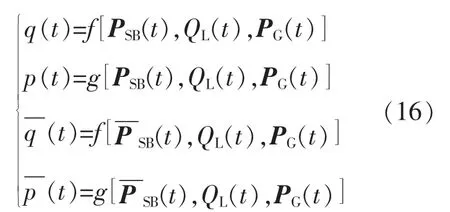
式中：PSB（t），PG（t）分别为合作博弈前 t 时段储能电站和发电商的竞价策略，其中，PSB（t）=[PSB，1（t），PSB，2（t），PSB，3（t）]，PSB，1（t），PSB，2（t），PSB，3（t）分别为 t时段储能电站三段式竞价策略的功率分段；PG（t）=[PG，1（t），PG2（t），PG，3（t）]，PG，1（t），PG2（t），PG，3（t）分别为 t时段发电商三段式竞价策略的功率分段；QL（t）为用户的购电电量策略为合作博弈后t 时段储能电站的竞价策略，其组成形式与PSB（t）相同。

合作博弈联盟主要在如下3 种情况下产生收益。

①当光伏电站出力充裕时，ΔP≥0，储能电站从光伏电站购买电量，扩大市场竞价的规模，获得更大的收益，并将一部分收益拿来作为对光伏电站的补偿。

②当光伏电站出力不足时，须视情况而定竞价策略。如果此时发电侧市场出清价高，则仍然可能ΔP≥0，储能电站向光伏电站购电，扩大市场竞价规模；光伏电站获得储能电站的补偿，用于支付不平衡功率惩罚后，收益仍然较高。

③当光伏电站出力不足，且市场出清价较低时，ΔP＜0，储能减少竞价规模，将节省的电量用于后续时段竞价，或者售电给光伏电站，用于不平衡功率平抑。光伏电站在降低惩罚费用的同时，储能电站也获得售电收益，达到双赢的效果。

分布式电源和储能组成联营模式也能起到能量协调的效果[21]。尽管联营模式能够更加充分地对储能电站和光伏电站的市场行为进行协调，进而获得更大效益，但联营模式不利于体现光伏电站和储能电站独自的市场价值，难以指导社会资本对两者的投资决策。

2.2 基于Shapley值的合作博弈剩余分配

当储能电站和光伏电站组成联盟时，必须保证两者收益不减，否则两个主体就会失去参与联盟的动力，该约束为

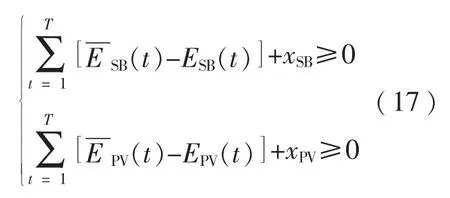
式中：xSB，xPV分别为合作博弈联盟向储能电站和光伏电站分配的合作剩余。

采用Shapley 值法进行计算，计算式如式（18）～（20）所示[22]。

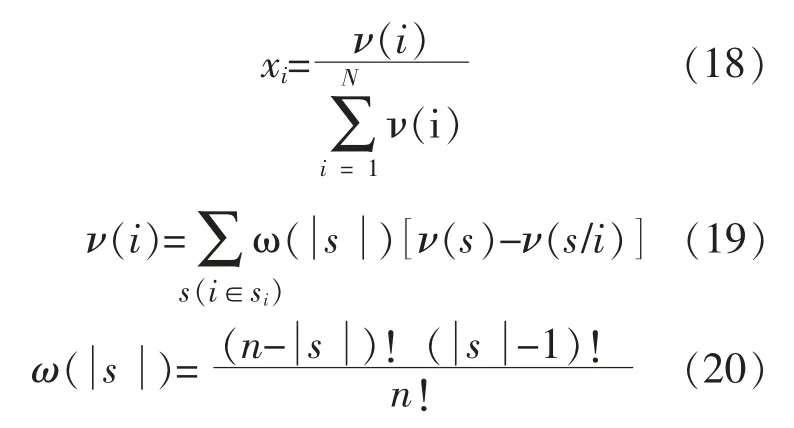
式中：si为联盟中包括参与主体i 的所有子联盟组成的子集；│s│为子集 s 的元素数目；ω（│s│）为加权因子；ν（s）为子联盟 s 的合作剩余；ν（s/i）为子联盟除去参与主体i 后的合作剩余；i∈{SB，PV}。

假定合作博弈联盟由N 个主体组成，则Shapley 值衡量了参与主体i 在进入联盟前后对联盟带来的综合边际收益。因此，用Shapley 值来分配联盟的合作剩余是比较公平合理的。

另外，合作博弈联盟的运行还须要满足内部交易电量约束：

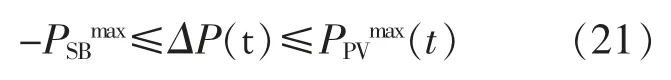
式中：PPVmax（t）为 t 时段光伏实际最大出力。

2.3 合作博弈模型的Nash均衡分析

合作博弈模型中设定一个联盟决策者的角色作为博弈领导者，储能电站和光伏电站作为从属者。两个从属决策者在领导者的决策下达成的博弈均衡叫做Nash 均衡。领导者和从属者达成的博弈均衡叫做Stackelberg 均衡。根据所建立的模型，本文合作博弈联盟中实际有3 个决策者，分别为联盟代理制定的内部交易电价策略、储能电站制定的运行策略及市场竞价策略、光伏电站制定的交易电量策略。

事实上，将联盟策略看作主体决策者，将储能电站和光伏电站看作从属决策者，则可以得到对于任意 p0下，合作博弈模型的 Nash 均衡[PSB*，ΔP*]。其中：对于∀PSB≠PSB*，式（22）成立；对于∀ΔP≠ΔP*，式（23）成立。

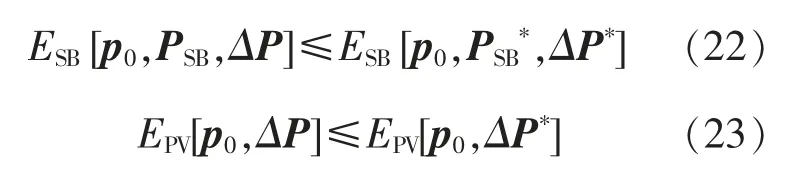
式中将储能电站一天的运行收益看作PSB，p0和ΔP 的函数，将光伏电站一天运行收益看作p0和ΔP 的函数。

另外，可以得到模型的Stackelberg 均衡为ESB[PSB*，p0*，ΔP*]。其中：对于∀p0≠p0*，式（24）成立。

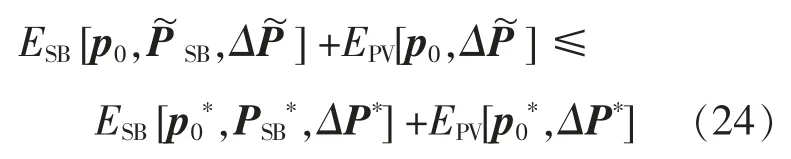
以下规划都须要满足必要的约束条件：

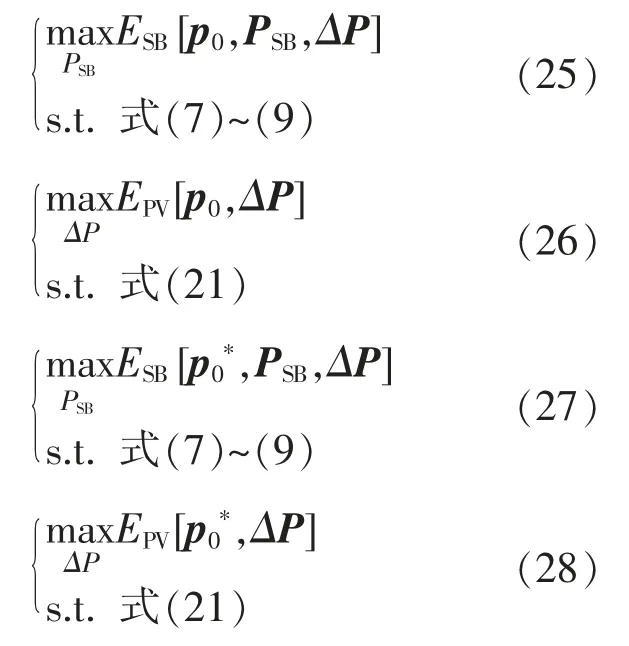
3 算法与模型求解流程

3.1 混沌粒子群算法

本文采用混沌粒子群算法设计合作博弈模型的求解流程。混沌粒子群算法中种群的速度和位置更新分别为

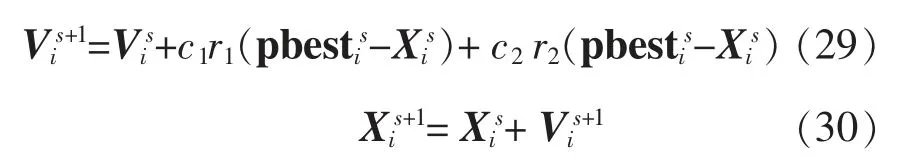
在每一次迭代后采用如下的Logistic 映射进行混沌搜索。

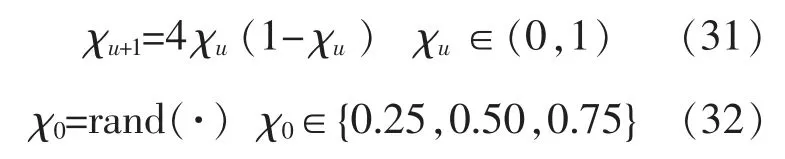
式中： χu+1，χu分别为第 u+1 次、第 u 次迭代时的混沌变量值；χ0为混沌变量初始值。

3.2 模型求解流程

根据以上混沌粒子群算法的基本原理，可以设计基于混沌粒子群算法的合作博弈模型的求解流程。

①根据随机初始化储能电站的报价策略，调度运行方案以及联盟内部的交易电量计划和交易电价曲线。初始化混沌粒子群算法参数：最大迭代次数为300；混沌搜索代数为30 代；学习因子为2；惯性系数为0.8。

②计算所有粒子对应的联盟竞价和运行方案下的目标函数，即参与电力市场竞价收益。

③根据各粒子对应的电力市场竞价收益，将约束条件作为罚函数出力，计及到该目标函数中，计算各粒子的适应度函数值。

④记录种群中的全局历史最优粒子以及每个粒子的历史最优情况。

⑤令每一个粒子根据全局最优粒子和历史最优粒子改变位置来寻优，并将改变后的每个位置粒子引入混沌算法，在局部区域进行混沌搜索。

⑥根据混沌粒子群算法收敛条件判断算法是否收敛。如果收敛，得出全局最优解及其对应的合作博弈联盟报价策略、调度运行方案以及联盟内部的交易电量计划和交易电价曲线；否则返回步骤②。

4 算例

4.1 算例设置

本文构造的电力市场中接入了3 个发电商（G1，G2，G3），其中，G1 为保守型发电商，G2 为中庸型发电商，G3 为投机性发电商。 3 个发电商的竞价参数参考文献[15]。此外，系统中还并网接入了一个储能电站和一个光伏电站作为市场主体。光伏电站并网容量为0.3 MW，储能电站最大出力为0.1 MW，储能电站容量为1 MW·h。电网公司代理作为对整个输配电网络的拥有者，对整个系统进行管理，并作为市场的组织者有权对各个市场主体的行为进行约束。电力市场运行时段长为0.5 h。为了比较储能电站与光伏电站合作博弈的效果，设置储能电站为独立运营模式与合作博弈模式两种运营方式。电力市场中，典型日一天的综合负荷水平曲线、光伏电站实际出力曲线如图1 所示。从图1 中可以看出，电力市场中负荷水平具有明显的峰谷特性。

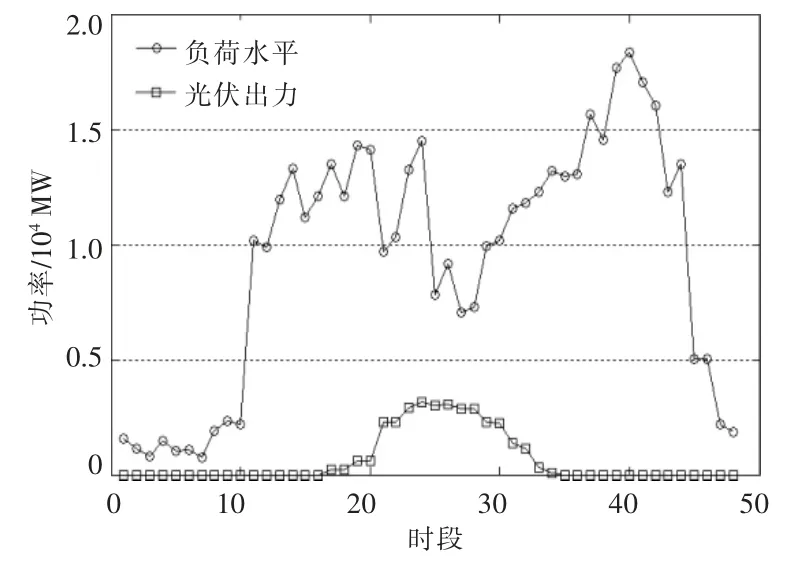
图1 电力市场典型日中光伏发电和负荷水平曲线Fig.1 Photovoltaic power generation and load level curve in a typical day of electricity market

4.2 仿真结果

运行本文所建立的模型，可以得到典型运行日电力市场发电侧一天的出清电价曲线、电网公司代理制定的销售电价曲线和储能电站及光伏电站组成合作博弈联盟的内部交易电价曲线（图2）。

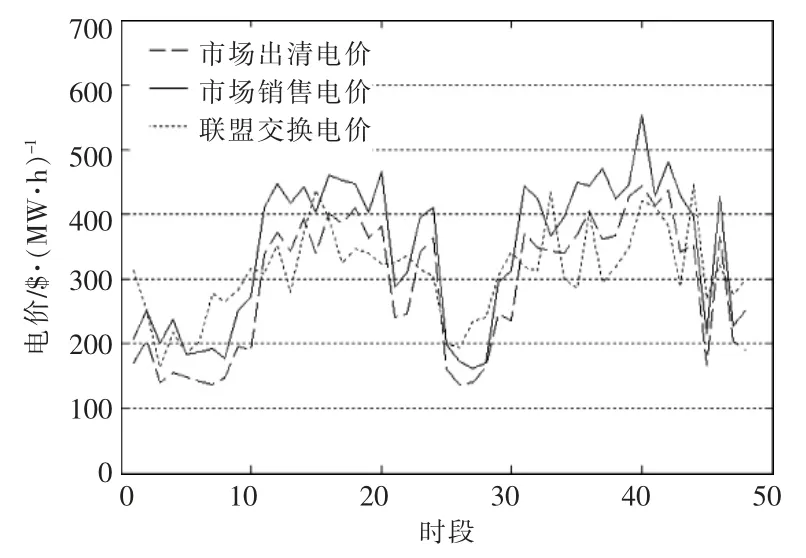
图2 电力市场博弈后市场出清电价曲线、销售电价曲线及联盟内部交换电价曲线Fig.2 Market clearing price curve，sales price curve and inter-alliance exchange price curve in power market game

从图2 中可以看出，市场出清电价曲线基本上随着综合负荷水平的变化而变化，并随着负荷水平的上升而增高。在第1～10 时段，系统综合负荷水平较低，无论是传统发电商还是储能电站，都能够根据经验存在一个对系统低负荷水平的预期。因此，为了尽量获得中标电量，趋向于申报较低的报价曲线。在这种情况下，系统中保守型的发电商有着更优的中标优势，而保守型发电商的报价曲线降低了电网公司代理制定的出清电价。

在第12～26 时段，系统综合负荷水平较高，无论是传统发电商还是储能电站，都能够根据经验存在一个对系统高负荷水平的预期，此时电力市场相对处于功率紧张时段，发电商和储能电站都更容易获得中标电力，因此都趋向于申报较高的报价曲线。在这种情况下，积极型发电商更具备中标优势，拉高了电网公司代理制定的市场出清电价。

在后续的综合负荷低谷时段和负荷高峰时段，对电力市场的分析也与上述时段相同。由于电网公司代理在制定市场出清电价时，不仅考虑经济因素，也须考虑系统电气运行约束（如支路传输容量限值、发电商的出力受出力限值的约束和机组组合约束），因此图中所示的市场出清电价曲线又不完全只与综合负荷水平有关。

从图2 中还可以看出，系统中线路输送功率越紧张，电网公司代理制定的销售电价水平与出清电价水平之差越大，以缓解紧张局面，并提高电网公司代理收益。相比于出清电价曲线和销售电价曲线，联盟内部的交换电价水平在不同运行时段具有不同的特征。当储能电站向光伏电站销售功率时，联盟内部电价高于市场出清价格，同时小于不平衡功率惩罚价格，以保证储能电站和光伏电站的双赢。

在储能电站与光伏电站组成合作博弈联盟的情况下，可以得到电力市场中各个主体一天的收益情况和合作博弈联盟内部的运行情况，包括联盟内部交换功率曲线、光伏电站不平衡功率曲线和储能电站充放电功率曲线（图3）。在这种情况下，其他发电商总收益达到了1 312 869 美元/d，而储能电站总收益达到了29 645 美元/d，光伏电站总收益达到了78 615 美元/d。

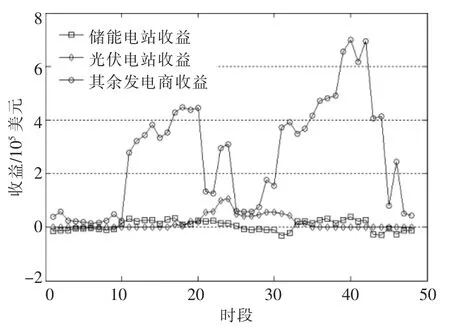
图3 储能电站、光伏电站和其他发电商一天收益曲线Fig.3 Benefit curves of energy storage power stations，photovoltaic power stations and other generation companies in a day

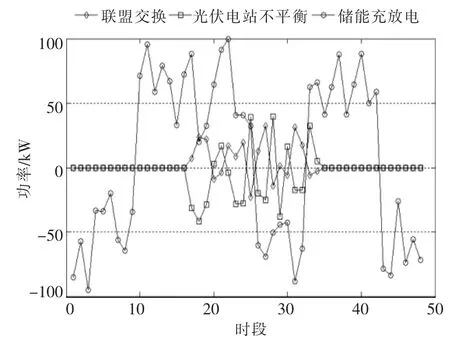
图4 合作博弈联盟内部交换功率、光伏电站不平衡功率以及储能充放电曲线Fig.4 Internal exchange power，unbalanced power of photovoltaic power station and charge-discharge curve of energy storage in cooperative game alliance

从图4 中可以看出，由于其他发电商承担了电力市场中大部分的中标电量，因此其收益水平远远高于储能电站和光伏电站。对于储能电站来说，在一天的第1～10 时段，市场出清电价较低，储能电站在用户模式下运行，向市场购电进行充电，并向市场支付销售电价。在第11～25 时段，市场出清电价高，储能电站在发电商模式下运行，参与发电侧的市场竞价并获取收益。在第26～33时段，储能电站再一次在用户模式下运行，为后续的放电做好准备。在该时段中，储能电站收益为负，即存在购电成本。在第34～42 时段，市场再一次运行在负荷水平和电价水平的峰时段，储能电站也再一次在发电商模式下运行。由此可以看出，储能电站利用自身的削峰填谷效益获得收益。对于光伏电站以及合作博弈联盟来说，光伏电站只在第17～35 时段存在出力的情况下才能获取收益。同时，光伏电站的不平衡功率基本上都通过储能电站加以平抑，避免付出高昂的惩罚费用。

实际运行中，储能电站还能和光伏电站作为一个电力市场主体在联营模式下运行。表1 给出了储能电站在4 种运行方式下各电力市场运行的收益情况。其中：方式1 为不参与电力市场；方式2 为独立运营模式；方式3 为与光伏电站联营模式；方式4 为与光伏电站合作博弈。

表1 电力市场博弈综合运行分析Table 1 Power market game comprehensive operation analysis 美元

当储能电站未参与电力市场时，一天的综合收益为零。在该方式下，光伏电站、其他发电商以及电网公司代理均有一定的收益，分别为68 157 美元，1 296 348 美元和 52 369 美元。

储能电站在独立运营模式下，能够获得一定的收益，但这收益是以光伏电站以及其他发电商的收益降低为代价的。在负荷水平一定的情况下，针对同样的市场出清电量，必然会出现这样的情形。对于其他发电商来说，储能电站的参与使发电商中保守型报价策略更加占优，以弥补电量不中标的风险，因此，其他发电商的收益比储能电站未参与时降低。对于电网公司代理来说，由于储能电站的加入，市场多样性得到了加强，电网公司代理作为市场出清电价制定者和向发电侧的购电者，其买方市场地位得到加强，因此电网公司代理收益得到了提升。

当储能电站与光伏电站联营时，由于两者的能量互补协调，储能电站和光伏电站的收益都得到了提高。这种方式下，联营主体对市场出清电价的稳定作用更加明显，其他发电商的收益也得到了显著提升。但是，对于电网公司代理来说，其收益提升不明显，因为这时发电侧的联营体作为新的市场主体，产生了一定的垄断效应。在联营模式下，储能电站和光伏电站不存在各自的运行收益。当储能电站与光伏电站在合作博弈方式下运行时，由于储能电站能够充分运用与光伏电站之间的电量协调，其收益要高于独立运营方式。这时，光伏电站的收益比储能电站独立运营方式下得到了提高，从66 154 美元提高到了78 615 美元。对于发电商来说，储能电站与光伏电站合作博弈，尽管仍然会与发电商竞争，但储能电站的参与对电力市场电价起到了稳定的作用，促进发电商制定更加激进的报价策略，从而提高收益。然而，这种情况下储能电站效益仍然明显，而发电商的收益仍然低于储能电站未参与电力市场时。对于电网公司代理来说，储能电站与光伏电站进行合作博弈，最重要作用是降低了电网公司代理对光伏电站收取的不平衡电量费用，因此电网公司代理的收益低于储能电站独立运营方式。