Lp-Blaschke-Minkowski同态的Shephard问题

富 娜,陈 斌

(1．西南交通大学 数学学院，四川 成都 610031；2．三峡大学 理学院，湖北 宜昌 443002)

0 引言

设K是一个凸体,如果K是n维欧式空间n中具有非空内点的紧的凸集.在n中所有凸体的集合写作Kn.令表示包含原点为内点的凸体集合,表示原点对称的凸体集合.此外,令表示在n中的星体集合(即包含原点且具有连续的径向函数的紧的星形).表示原点对称的星体集合.我们记u为单位向量,B为质心在原点的单位球, 其表面记为Sn-1.

投影体的概念是由Minkowski在上世纪末首次引入的.通过Petty[1], Schncider[2], Bolker[3], Lutwak[4]和张高勇[5]等人的工作,投影体的研究引起了许多国内外学者的关注.

h(K,x)=max{x·y∶y∈K},x∈n

其中x·y表示n中x和y的标准内积.

假设K∈Kn,任意的u,v∈Sn-1,K的投影体∏K是原点对称的凸体,并且有如下的支撑函数:

其中S(K,·)表示K的表面积测度.

关于投影体,Shephard[7]提出了如下的问题：

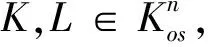
V(K)≤V(L).

问题1.1被称为Shephard问题,比问题1.1中条件更广泛的一类问题称之为一般Shephard问题.对于问题1.1的解答,Petty[1]和Schneider[2]分别给出了肯定与否定回答.

关于投影体的更多知识可以参考下面的两本非常好的书(见文献[6,19]).

2006年,在投影体性质的基础上,Schuster[8]介绍了Blaschke-Minkowski同态的概念,并在此概念的基础上研究了Shephard问题.关于Blaschke-Minkowski同态的更多知识可以参考文献[9～13].2013年,汪卫又将Schuster介绍的Blaschke-Minkowski同态概念推广到了Lp形式,在此,根据Lp Minkowski存在定理[14](定理9.2.3)，我们改进汪卫的Lp-Blaschke-Minkowski同态的概念如下：

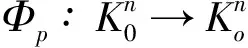
1)Φp是连续的；

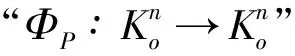
有关Lp-Blaschke-Minkowski同态的更多知识可以参见文献[15～17].

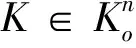
(1.1)

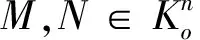
在本文中,结合Lp仿射表面积的概念,我们继续研究Lp-Blaschke-Minkowski同态的Shephard问题.

(1.2)

结合式(1.2),我们给出Lp-Blaschke-Minkowski同态的Shephard问题的肯定回答如下：

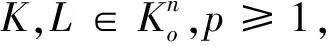
(1.3)

等号成立当且仅当ΦPK=ΦPL.

(1.4)

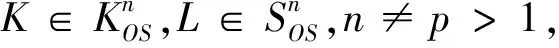
(1.5)

等号成立，当且仅当ΦPK=ΦPL.

最后,我们给出Lp-Blaschke-Minkowski同态的Shephard问题的否定回答.

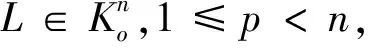
ΩP(K)>ΩP(L).

(1.6)

以下,我们介绍一些基本的概念.定理1.1～1.3的证明将在第二节给出.

1 预备知识

1.1 径向函数和极体

ρ(K,x)=max{λ≥0∶λ·x∈K},x∈n{0}.

如果ρK是一个连续的函数,则称K是一个关于原点的星体.如果K,L∈Sn,且ρk(u)/ρL(u)与u∈Sn-1无关,则称K，L是彼此膨胀的.

设E∈Kn的极体E*定义为[19]

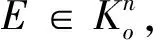
(2.1)

1.2 Lp混合体积和Lp对偶混合体积

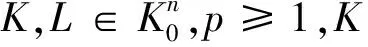
dSp(K,·)=h(K,·)1-pdS(K,·),

其中S(K,·)是K的表面积测度.

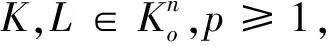
(2.2)

(2.3)

由式(2.2)和式(2.3),我们容易得到

V-p(K,K)=Vp(K,K)=V(K).

1.3 Lp-Blaschke体

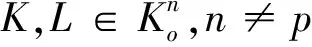
Sp(λ⊙K∓pμ⊙L,·)=λSp(K，·)+μSp(L，·),

(2.4)

其中∓p表示Lp-Blaschke加,⊙表示Lp-Blaschke数乘.

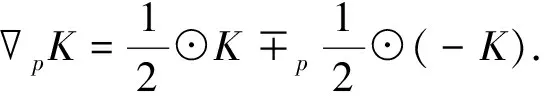
(2.5)

2 Lp-Blaschke-Minkowski同态的Shephard问题

在本节中,我们给出Shephard问题,即定理1.1～1.3的证明.首先,我们给出下面的引理，以证明定理1.1.

Vp(K,ΦpL)=Vp(L,ΦpK).

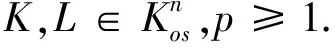
h(ΦpK,u)p≤h(ΦpL,u)p

(3.1)

=Vp(L,ΦpN)=Vp(N,ΦpL).

(3.2)

在式(3.2)中等号成立当且仅当ΦpK=ΦpL.

根据式(3.2)中等号成立的条件,我们可以得到式(1.3)中等号成立当且仅当ΦpK=ΦpL.

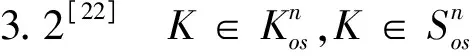
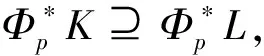
(3.3)

(3.4)

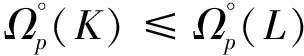
根据式(3.4)等号成立的条件,我们得到式(1.5)中等号成立当且仅当ΦpK=ΦpL.

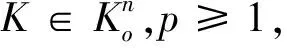
由引理3.3,我们立即可以得到下面的结果：

Ωp(-K)=Ωp(K).

(3.5)

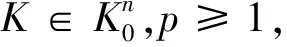
Ωp(pK)≥Ωp(K)

(3.6)

当p=1时,等号成立当且K的质心在原点,当p≥1时等号成立，当且仅当K是原点对称的.

证明结合式(1.1)和式(2.5),我们得到

则通过式(3.5),我们可以得到式(3.6)，并且在式(3.6)中当等号成立，当p=1时,等号成立当且K的质心在原点；当p>1时,等号成立当且仅当K是原点对称的.

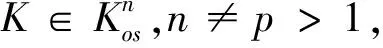
h(ΦpK,·)p=Sp(K，·)*g,

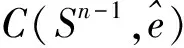
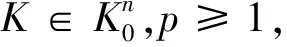
h(Φp(pK),u)p=Sp(pK,u)*g

当Φp是偶的时,则ΦpK=Φp(-K).因此我们得到Φp(pK)=ΦpK.

定理1.3的证明当L不是原点对称的,利用引理3.4,我们得到

Ωp(pL)>Ωp(L)

取一个ε>0,使得Ωp((1-ε)pL)>Ωp(L),并且令K=(1-ε)pL,则Ωp(K)>Ωp(L).