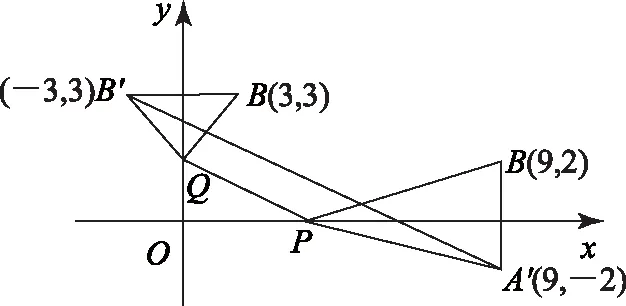
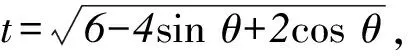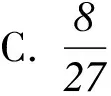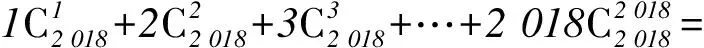2018年北京大学博雅计划自主招生数学试题(部分)及其详解

◇ 北京 甘志国(正高级教师)

2018年北京大学博雅计划自主招生数学试题包括20道单项选择题,每道题答对得5分,答错扣1分,不答得0分.本文是考生回忆版,缺少第7,8,18,19,20题,试题中第2,14,17题是数列问题,第11题是方程问题,第4题是三角函数问题,第5题是不等式问题,第10,13题是平面解析几何问题,第6,15,16题是排列组合问题,第1题是古典概型问题,第9题是复数问题,第12题是平面几何问题,第3题是数论问题.整体难度不大，本文给出其详细解析，供读者参考.

1. 一个集合中有10个两两互异的元素,若有放回地取,则在前5次内取到相同元素的概率为( )(保留两位有效数字).

A. 0.50 B. 0.55

C. 0.70 D. 前三个答案都不对

3.若正整数n的全部正约数之积是n3,且n≤400,则n的个数是( ).

A. 50 B. 51

C. 55 D. 前三个答案都不对

当m=1时,J(m)=1.

y1yg(m)=y2yg(m)-1=y3yg(m)-2=…=
yg(m)-1y2=yg(m)y1=m.

所以由倒序相乘法可得

J(m)=y1y2y3·…·yg(m)-1yg(m),
J(m)=yg(m)yg(m)-1yg(m)-2·…·y2y1.

因而

下面用该结论来解答本题.

当n=1时，满足题设:J(1)=1=13.

若p1=2,可得3≤p2≤97,此时n的个数是24;若p1=3,可得p2≤43,此时n的个数是13;若p1=5,可得p2=2,3,7,11,13,此时n的个数是5;若p1=7,可得p2=2,3,5,此时n的个数是3;若p1=11,可得p2=2,3,此时n的个数是2;若p1=13,可得p2=2,此时n的个数是1;若p1≥17,可得p2不存在,此时n的个数是0.

综上所述,可得所求答案是51，故选B.

A. 0 B. 1

C. 无穷多个 D.前三个答案都不对

进而可得

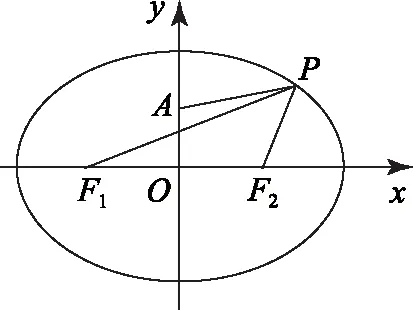
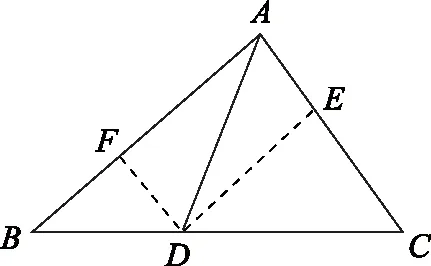
5. 若非负数a,b,c满足a+b+c=3,则a+ab+abc的最大值是( ).

A. 3 B. 4

设g(a)=a3-8a2+20a(0

6.15个人围坐在圆桌旁,从中任取4人,他们两两互不相邻的概率是( ).

进而可得

且

图1

A. 2 B. 3

C. 4 D. 前三个答案都不对

图2

再由S△ABC=1,可得

图3

所以

方法2我们先证明一个结论.

结论如图4所示,点D在△ABC的边BC上且不是端点.

(1)若BD∶DC=λ∶μ,则

图4

证明(1)如图5所示,过点D作DE∥AB且DE交AC于E,作DF∥AC且DF交AB于F,得

再由平面向量基本定理可得

图5

下面用结论来解答本题.

再由平面向量基本定理,可得

A. [10,11] B. (11,12]

C. (12,13] D. 前三个答案都不对

图6

14. 已知a,b,c是公差不为0的等差数列,在平面直角坐标系xOy中，过点P(-3,2)向直线ax+by+c=0作垂线,垂足为M.若点N的坐标是(2,3),则|MN|的最大值与最小值之积为( ).

C. 14 D. 前三个答案都不对

图7

再由点N(2,3)在圆C外,可得

15.从所有不大于2 018的正整数中任取3个,3个数两两不相邻的选法种数有( ).

……

综上所述,3个数两两不相邻的选法种数为

故选A.

综上所述,3个数两两不相邻的选法种数为

方法4本题也可用正难则反的方法来求解.

当所取的3个数两两相邻时,有2 016种取法，即i,i+1,i+2(i=1,2,3,…,2 016).

当所取的3个数恰有两个相邻时,包括下面的2 015×2+2 014×2 015=2 015×2 016种情形.

1,2,n(n=4,5,6,…,2 018)的形式,共2 015种;

2,3,n(n=5,6,7,…,2 018)的形式,共2 014种;

3,4,n(n=1,6,7,8,…,2 018)的形式,共2 014种;

4,5,n(n=1,2,7,8,…,2 018)的形式,共2 014种;

……

2 015,2 016,n(n=1,2,3,…,2 013,2 018)的形式,共2 014种;

2 016,2 017,n(n=1,2,3,…,2 014)的形式,共2 014种;

2 017,2 018,n(n=1,2,3,…,2 015)的形式,共2 015种.

综上所述,3个数两两不相邻的选法种数为

注本题与2017年清华大学能力测试数学试题中的一道题实质相同,即

已知集合A={1,2,3,4,5,6,7,8,9,10},若从中取出3个元素构成集合A的子集,且所取得的3个数互不相邻,则这样的子集个数为( ).

A. 56 B. 64 C. 72 D. 80

A. 2 018·22 018B. 2 018!

C. 2 019·22 018D. 前三个答案都不对

所以

17.若把全体正整数中的完全平方数全部去掉后,再把剩下的数从小到大排列得到一个新数列,则该数列的第2018项是( ).

A. 2 062 B. 2 063

C. 1 009 D. 前三个答案都不对

但该数列中又有一个完全平方数2 025，即452,所以还要去掉它,因而目前得到的新数列的第2 018项是2 062+1=2 063.

又由452=2 025<2 063<2 116=462,可知2 063不是完全平方数,故选B.