基于响应面法的起重机结构可靠性灵敏度分析
2020-04-13张焕梅杨瑞刚
张焕梅,杨瑞刚
(1.太原工业学院机械工程系,山西太原030008;2.太原科技大学机械工程学院,山西太原030024)
起重机工作环境复杂,一旦发生事故,会产生机毁人亡的后果。因此,起重机安全事故不仅给国民经济造成损失,还有损民族企业的形象,降低企业的市场竞争力。如何进一步保证起重机的安全性与可靠性是我国起重机制造业发展面临的重要课题之一。
可靠度计算方法大多是以显式表达式作为极限状态方程。当分析计算没有显式的失效函数时,求解存在一定困难。基于响应面法(Response Surface Method,RSM)提出了一种可近似建立模型及计算分析方法解决这一问题。Wong[1]在分析土坡稳定的可靠度时,开创性地提出了RSM;Bucher等[2]将RSM引入结构可靠性分析中,建立结构输入与结构响应之间的关系;陈铁冰等[3]将RSM应用在桁架桥可靠度分析中;武清玺等[4]提出变f序列的RSM和相应的收敛控制准则应用在大型复杂结构的可靠度分析中;Sayan等[5]提出一种改进的响应面函数,并且就构成响应面函数的各变量,在功能函数中对失效概率影响的贡献大小对变量排序;胡冉等[6]提出考虑变量之间相关性的随机RSM;Yoo等[7]采用连续标准RSM对结构进行可靠性拓扑优化;徐尧等[8]利用多元回归分析技术,以显式的响应面模型逼近模型参数与响应特征之间的隐式函数关系;蔡斌等[9]在灵敏度与可靠度的分析中,基于RSM将可靠性指标函数表示为随机变量的显式;张春宜等[10]将智能算法与双重RSM相结合,提出可靠性灵敏度分析的智能双重RSM。
本文采用Visual Studio软件和ANSYS有限元软件的APDL语言,对通用桥式起重机结构进行分析。通过对通用桥式起重机有限元建模、网格划分、定义边界条件,分析不同工况下的载荷,在基于有限元的概率设计技术(Probabilistic Design System,PDS)模块中,分析研究了起重机的RSM可靠性与灵敏度关系,为设计人员提供了理论和技术指导。
1 基本理论
1.1 响应面结构可靠性计算方法
对结构可靠度分析而言,RSM指运用有限元数值计算拟合一个函数面替换难以确定的复杂的极限状态函数,从而能够对结构可靠度进行分析求解。使用有限的试验结合回归拟合出可靠性解析表达式Z'=g'(X),替换真实的高阶非线性曲面Z=g(X)。当基本随机变量值为2时,响应面如图1所示。

图1RSM示意图Fig.1 The response surface method
对含n个随机变量常用如下不含交叉项的二次多项式函数:

式中:a,b,c为表达式的待定和修正系数。
对有n个随机变量的响应面函数有2n+1个待定系数,对于系统的确定和整个表达式的修正可按照以下步骤计算:
步骤1先选择一个较为合适的假定迭代点X(1)=(,…,),初次计算一般可以取均值点;
步骤2用试验计算功能函数(复杂结构的可靠度分析一般采用数值模拟试验,如有限元计算)Z=g(,…,)以及Z=g(,…,σi,…,),可以得到2n+1个点的估计值,其中,系数f在第一轮估计中通常取2或3,在以后的迭代计算中常取1,为X的均方差;
步骤3由上面步骤2求得的2n+1个点的估计值,从而能够求得a,最终就可以确定结构的近似极限状态函数;
步骤4采用JC法或者其他可靠度求解法求解可靠度指标,k代表第k次迭代;
步骤5如果|β(k)-β(k+1)|<ε停止迭代(为收敛精度条件),否则利用插值法获得新的展开点:

通过插值可使点十分靠近极限状态曲面,以为迭代点返回步骤2进行迭代,直至满足精度条件为止。
1.2 基于RSM的可靠性灵敏度分析方法
通常选取线性或二次多项式函数作为近似函数,选取可靠性指标函数的近似函数的完全二次多项式:

式中:n为设计变量的;αi与αij为待定系数。
可靠度对基本随机变量X分布参数的灵敏度为

2 桥式起重机主梁的载荷分析
桥式起重机金属结构载荷主要有自重、风压、起升载荷及变速运动引起的惯性与冲击等偶然载荷。起重机受到的载荷图谱如图2所示。
2.1 主梁的强度
主梁在垂直方向与水平方向联合作用下产生的最大应力σmax为

式中:σ(G+P)为最大弯矩处产生的正应力;σH为大车启动或刹车时会产生水平惯性载荷。则

图2 起重机桥架所受外载荷图谱Fig.2 Crane bridge by external load
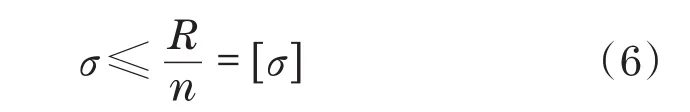
式中:n为安全系数;R为材料抗力值。
2.2 静态刚性指标
当主梁受到两个移动载荷力同时施加相同的力时,主梁跨中的静挠度为
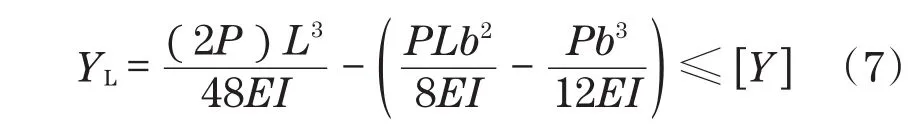
式中:P为作用在主梁上的小车轮压;L为主梁的跨度;E为材料的弹性模量;I为主梁截面折算之后的近似惯性矩;b为小车的轮距;[Y]为主梁的许用静刚度。
3 基于ANSYS RSM的桥机金属结构可靠性分析
3.1 基于ANSYS RSM的结构可靠性
利用ANSYS软件中RSM求解结构模型的可靠度,可以采用交互GUI方式(图形界面)和批处理方式(命令流文件),或把两者结合起来进行。ANSYS可靠性分析数据流向如图3所示。
3.2 基于VS对ANSYS开发的软件
根据以上原理,基于VS对ANSYS开发的软件界面如图4所示。
当所有的参数都设置完成后,可以在ANSYS分析组中单击生成命令流,即可给txt命令流文件命名并保存;单击命令流按键查找刚才生成保存的命令流文件,单击查找ANSYS程序就可以把本电脑中ANSYS的路径获取到,执行ANSYS分析功能就可后台调用ANSYS执行生成的命令流文件,分析完成后找到文件夹,文件夹里有分析结果。
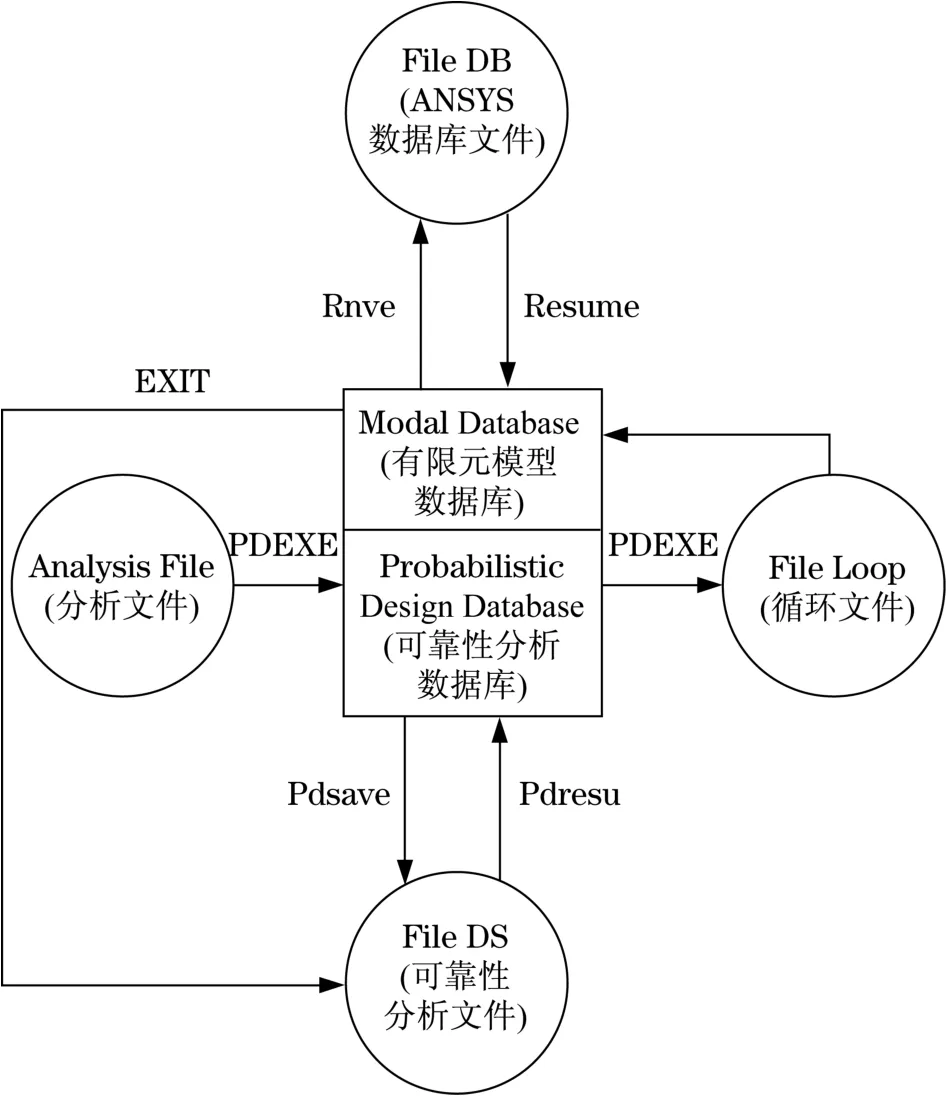
图3 可靠性分析数据流向示意图Fig.3 Reliability analysis of the data flow diagram
4 工程算例分析
4.1 工程算例
以某公司一台桥式起重机做为算例,该桥式起重机的参数如表1和表2所示。输入参数主梁翼缘板厚度T1、主腹板厚度T2和输出结果Z的柱状图及累积分布曲线图,从图5、图6、图7中可以得到该参数抽样的均值、标准方差、偏度系数。
4.2 静强度可靠性与灵敏度分析
静强度可靠性与灵敏度分析结果如图8所示。
图8反映了随机输入参数对强度失效的影响程度。从影响程度强弱可以分为重要参数(如B1,T2,…,H1)与不重要的参数(T3,T4,…,T8);从影响关系可分为正数与负数的关系,正数代表输入参数与输出参数是正比例关系,负数代表它们是反比例关系。
4.3 静刚度可靠性与灵敏度分析
静刚度与灵敏度分析结果如图9所示。
图9反映了重要的参数(如H1,T1,…,T3)与不重要的参数(T4,T5,…,T8)。

图4 软件主要界面图Fig.4 The software main interface

表1 桥架结构主、端梁截面尺寸Tab.1 Section size of beam and end beam of bridge structure

表2 桥式起重机的参数和数值Tab.2 Parameters and values of the bridge crane
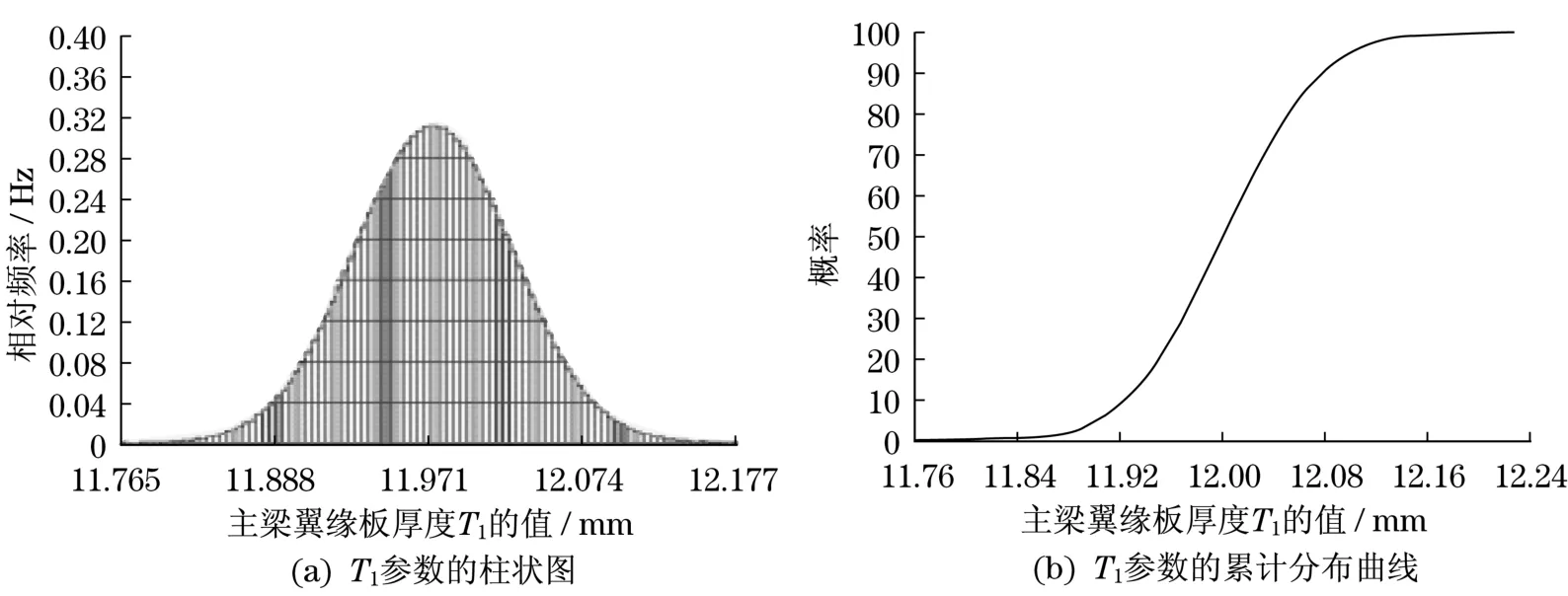
图5 T1参数的柱状图及累积分布曲线图Fig.5 T1parameters histogram and cumulative distribution curve
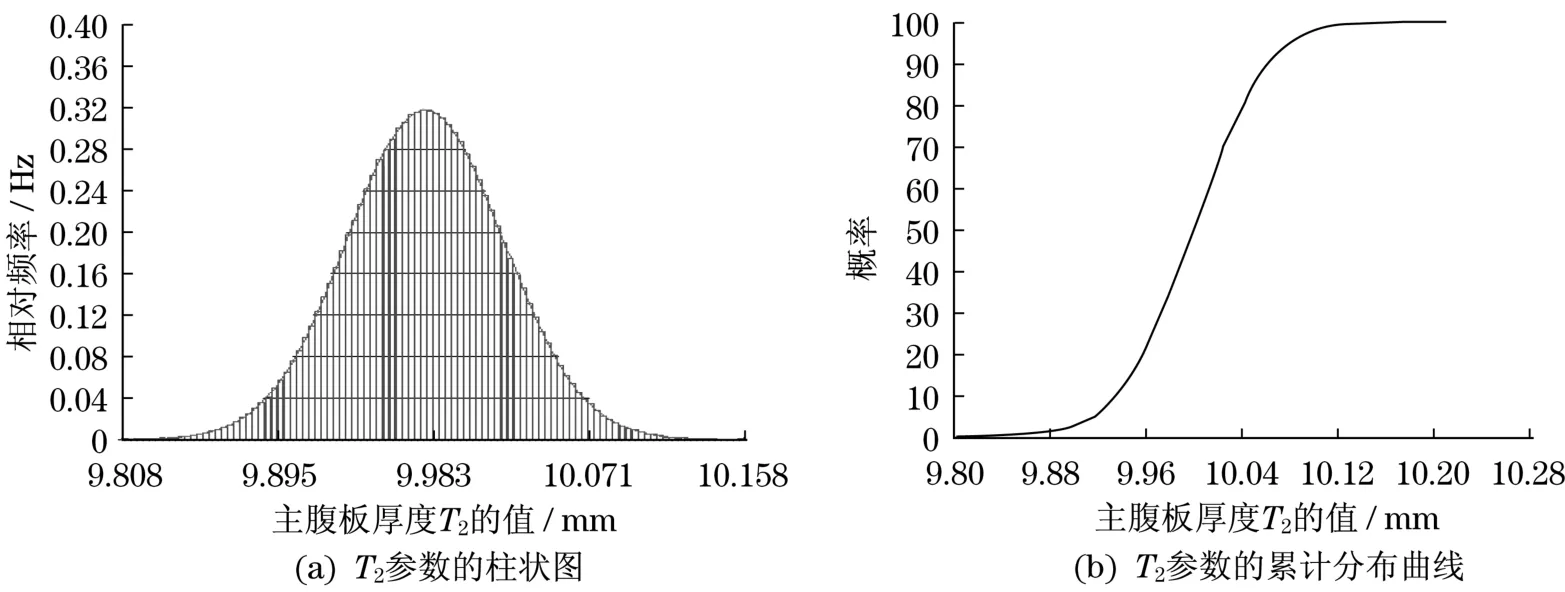
图6 T2参数的柱状图及累积分布曲线图Fig.6 T2parameters histogram and cumulative distribution curve

图7 输出参数z的柱状图及累积分布曲线图Fig.7 Output parameter z of histogram and cumulative distribution curve

图8 输入参数的灵敏度图Fig.8 The sensitivity of the input parameters
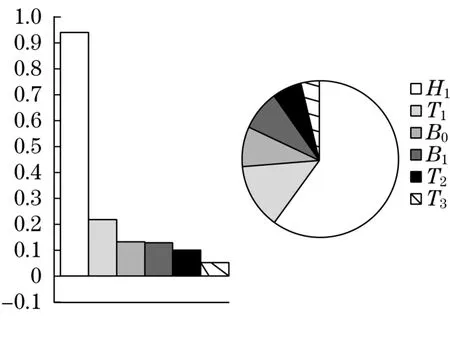
图9 输入参数影响输出参数的灵敏度图Fig.9 Input parameters affect the sensitivity of output parameters
5 结论
(1)利用Visual Studio软件开发设计了建模交互界面,并完成分析类型的选择、参数的输入、命令流的生成、选择命令流与ANSYS程序、执行分析一系列功能,提高了建模分析的效率。
(2)本文假设起重机主梁结构截面服从正态分布,研究了该起重机的强度、静刚度的可靠性与灵敏度,并分析其原因。
(3)影响起重机可靠性与灵敏度的参数因素多,本文在分析时只是选择了以主梁截面为主,并没有考虑其他因素对起重机的影响。
