基于谱熵与弯曲时间特征的性能退化GG聚类

王 微，胡 雄，王 冰，孙德建

（上海海事大学物流工程学院，上海201306）

港口起重机械是码头重要的物资装卸设备，轴承和齿轮是其中重要的旋转支撑部件，一旦发生突发性故障，轻则带来经济损失，重则导致人员伤亡。因此，采集并分析旋转支撑部件的运行监测信号，进而准确识别性能退化状态，能够降低旋转支撑部件发生突发故障的概率，提升港口起重机械的整机可靠性。港口起重机械工作在重载、高速性的工作环境下，旋转支撑部件的振动监测信号一般呈现出非线性、非平稳、非周期的特点，需要针对性地研究性能退化状态识别的方法。

性能退化状态识别的关键步骤包括退化特征提取与识别模型构建［1］，其中退化特征提取是构建识别模型的基础。特征参数的优劣决定着是否能够准确识别退化状态。常见的退化特征主要基于时域、频域以及时频域分析方法而提出，其中时域和频域因计算简单且有应用价值而被广泛采用，如信号的有效值、方差、平均频率等［2-3］。目前，大多数工程振动信号均体现出强烈的非线性以及非平稳性，以信息熵为基础的复杂度分析方法为该领域的研究提供了一条有效的途径。该类复杂度分析方法一般可以划分为行为复杂度算法和结构复杂度算法，行为复杂度算法中应用较多的包括模糊熵［4］、样本熵［5］、近似熵［6］等。该类方法计算过程一般涉及嵌入维数选取问题，结果受参数因素影响较多，且当数据长度增大时，运算速度随之变慢，实用性不足。

结构复杂度算法以傅里叶变换（FFT）为基础，能够度量序列的相关结构复杂性，参数少，计算速度快。典型的方法包括谱熵（Spectrum Entropy，SE）和C0复杂度方法。谱熵方法计算方便，不涉及中间参数，计算速度快，可以有效地分析短时、非平稳、有噪声干扰的数据［7］。文献［8］证明了SE和C0复杂度曲线能够正确有效地描述连续混沌系统的动力学特征。当前，SE算法主要应用在混沌系统的复杂性分析上，利用该算法分析机械设备性能退化规律的研究很少，因此，开展基于SE的退化特征分析具有一定的研究空间。

机械设备退化状态的在线识别一直是该领域的难点问题。本文重点研究其中的一个关键问题：退化状态的无监督离线识别，即通过无监督聚类方法分析特征数据的关联性，挖掘数据之间的内在规律，识别不同的退化阶段，从而为退化状态在线识别奠定基础。当前，应用较多的无监督聚类方法包括K-means［9］，FCM（Fuzzy Center Means）［10］，GG（Gath-Geva Fuzzy Clustering）［11］以 及 GK（Gustafaon-Kessel Clustering）［12］等。其中 GG 聚类算法采用了模糊最大似然估计距离范数，具有更优的聚类精度［13-15］。在关于GG聚类算法的研究中，研究热点主要集中在故障模式的诊断，对性能退化状态聚类的研究则相对较少，并且对性能退化中的时间连续性约束考虑较少，算法的性能还有进一步提升的空间。

综上，本文将SE方法应用于性能退化特征提取中，将时间参数映射到指数函数中，形成更符合退化过程的“弯曲时间参数”，并与SE、有效值构成三维退化特征向量，最后，采用GG模糊聚类算法实现不同退化状态的识别。设计序列离散度指标评估聚类的时间聚集度，采用来自美国智能维护系统（Intellegent Maintenance System，IMS）中心的轴承全寿命试验数据对方法进行验证。

1 SE定义

SE的主要思想是以傅里叶变换为基础，分析傅里叶变换得到频域内的能量分布，并基于香农熵理论而得到描述信号复杂度的指标。该算法的基本流程如下［16］：

（1）直流部分去除。假设x（n）为长度N的时间序列，利用下式去除掉信号的直流成分，从而使频谱更准确地表征信号的能量，即

（2）对去除直流分量的信号进行离散傅里叶变换，得

（3）计算相对功率谱。对经过离散处理后的频谱序列取其前半部分进行计算，并应用算法，得到其中一个特定频率的功率谱大小，即

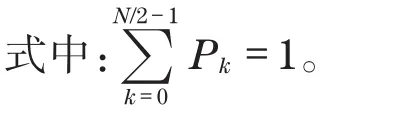
（4）以香农熵理论为基础，计算信号的SE为

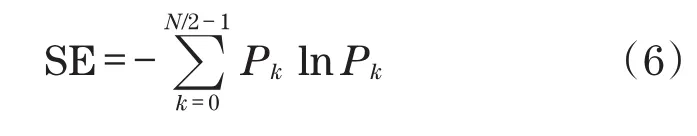
一般情况下，由于SE的最大值为ln（N/2），因此，一般会对SE进行归一化操作，得到如下归一化的SE，即

通过以上定义可以看出，SE能够描述信号的结构稳定性，如果功率谱变化情况越不稳定，则信号的结构组成越简单，其序列振幅越不明显，得到的测量值也较小。反之，信号的结构组成越复杂，参数的取值越大。本文采用SE对机械设备的性能退化特征进行描述。

2 退化过程识别流程

本文提出一种基于SE与弯曲时间特征的性能退化GG聚类方法，流程如图1所示。获得机械设备全寿命数据之后，分别经过退化特征提取、退化状态划分、聚类效果评价3个阶段，重点对弯曲时间特征以及聚类效果评价进行阐述。

图1 退化状态划分流程Fig.1 The flow chart of degradation condition

2.1 弯曲时间特征

为了提高特征向量的全面性，提取了信号的三维特征向量［RMS，SE，CT］。其中，均方根RMS能够表征信号的能量累积变化，SE复杂度能够反映信号复杂度变化，弯曲时间（Curved Time，CT）能够反映性能退化进程中的时间特征。计算方法是将全寿命时间参数T归一化并映射到函数CT=eT-1中，从而获得初期平缓、后期剧烈的“弯曲时间维度”，从而更准确地反映机械设备性能退化的时间分布特性，如图2所示。

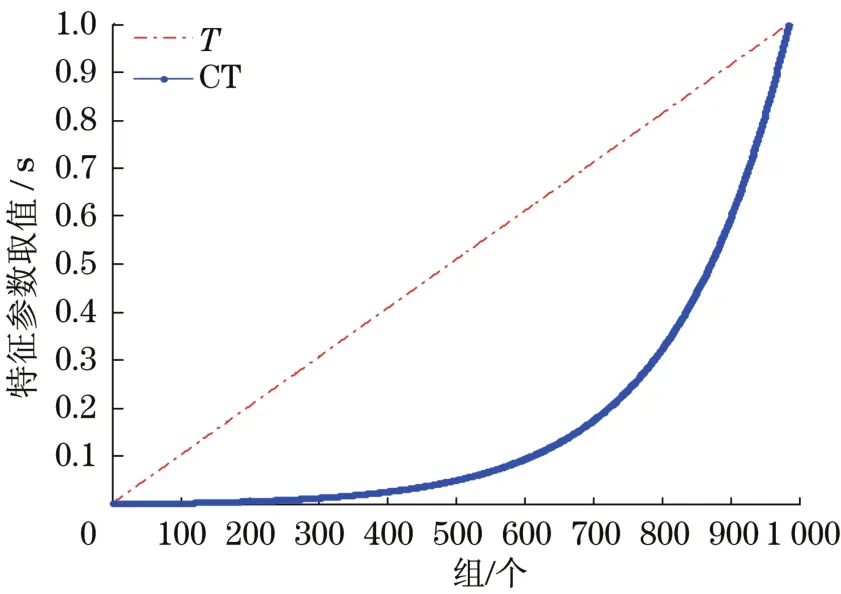
图2 时间参数与“弯曲时间参数”对比Fig.2 Contrast of T and CT

2.2 GG模糊聚类的效果评价

GG模糊聚类原理已在文献［17-18］中论述，在此不做详细展开。一般情况下，以模糊理论为基础的聚类算法均是采用隶属度最大原则进行类别聚类，判断的数据依据均是隶属度矩阵U。应用较多的两个指标分别为分类系数（Classification Coefficient，CC）以及平均模糊熵（Average Fuzzy Entropy，AFE）［11］。CC指标越接近1，AFE指标越接近0，模糊聚类的效果越好。

此外，退化状态的聚类最主要特征是同一运行状态的时间连续性。因此，提出一种序列离散度指标（Sequence Dispersion，SD），以此衡量同一类别样本时间标签的连续性。对于某个聚类，假设I为该集合的标签序列，n为该聚类的样本个数，m-1为该标签序列最大值与最小值之差，定义该聚类的序列离散度如下：

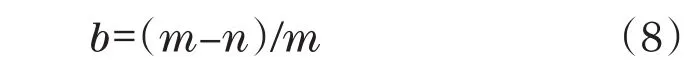
显然，如果I为连续序列，则b=0；I越不连续，序列中存在“空位”越多，序列离散度越大。

假设整个样本集合被划分为c类，则此次聚类的时间序列离散度计算如下：

该指标越接近于0，代表时间聚集度越高，退化状态聚类效果越好；取值越大，时间聚集度越低，聚类效果越差。

3 退化状态识别实例分析

本节采用的全寿命数据集来自辛辛那提大学IMS中心［21］。加速寿命实验台的示意图如图3所示。

图3 加速试验台Fig.3 The accelerated test bench

选取其中一组数据集进行分析，该组试验的负载为5 000 N，转速为1 500 r/min，采样频率为20 kHz，每组采样时间为1 s，组间采样间隔为10 min。数据集采样组数为984，最终失效形式为外圈故障。

3.1 退化特征提取

分别对每组采样数据进行退化特征分析，计算SE、RMS以及CT。图4为全寿命数据集的退化特征趋势图。

图4 轴承全寿命数据集下的性能退化特征趋势Fig.4 The performance degradation characteristic trend graph under bearing life data set

从图4可以看出：在整体趋势上，复杂参数随着性能退化程度加深而逐渐降低，有效值RMS的趋势则与之相反。这说明随着性能退化程度的增加，信号中的随机成分逐渐减少，信号的复杂度随之降低。而从能量累积观点上看，信号的能量随着退化程度的增加而不断增大，有效值RMS也随之增大。从细节上看，两个特征参数均呈现出一定的阶段性，反映了轴承性能退化的不同状态。另外，通过时间的“弯曲化”，CT参数与性能退化的整体趋势关联性更强。

3.2 退化状态识别

采用GG聚类算法进行退化状态聚类，参考同类文献，本文将退化状态划分为4个类别，设置参数为c=4，m=2，容差为ε=0.000 01。

GG聚类的退化状态识别结果如图5所示。整个退化过程聚集成4个阶段，分别定义为正常状态（Normal）、轻微退化状态（Slight）、严重退化状态（Severe）、失效状态（Failure），并且每个状态在时间尺度的连续性较好。从图5（a）可以看出，在约第520组采样点之前，轴承一直保持较长时间的正常状态，SE取值维持在0.7附近。当轴承性能轻微退化时，SE曲线非常敏感并快速下降，并出现明显的波动现象。进入到约第820组采样点后，轴承性能严重退化，SE曲线基本维持在0.4左右，数值反弹不大。当进入到失效状态时，退化特征参数总体较低，且出现一些数值异常的离散点，此时认为轴承已经完全失效。4个分组的序列离散度分别为0.001 9，0.065 1，0.050 0，0.410 3，本次分类的总的序列离散度为0.527 2。

图5 GG聚类效果图Fig.5 Graph of GG clustering effect

3.3 CT特征分析

分析CT特征参数对于聚类效果的影响。保持GG模糊聚类算法和参数设置不变，分别采用二维特征［SE，RMS］和三维特征［SE，RMS，T］进行对比分析，其中T为未进行映射的时间参数。图6为两种方案的聚类效果图，表1为聚类的定量评价结果对比。

图6 不同特征参数的聚类效果Fig.6 Clustering effect diagram of difference feature parameters

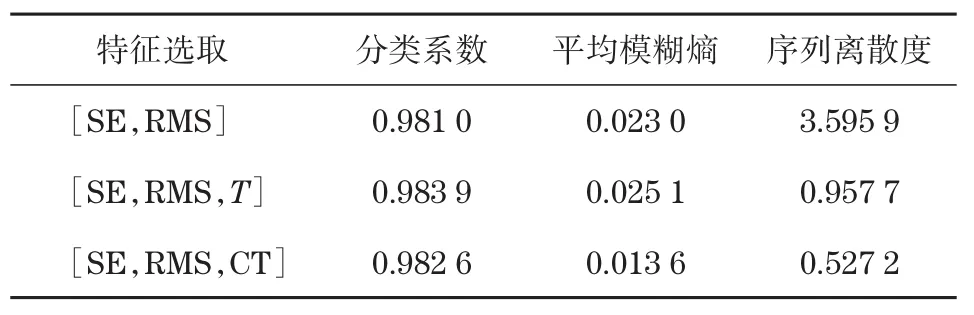
表1 不同特征参数的定量评价结果Tab.1 Quantitative evaluation results of different characteristic parameters

对比可以看出，3种方法在分类系数和平均模糊熵参数上取值相近，但序列离散度取值较大，说明聚类的时间集聚性较差，从图6中同类状态的不连续性也可以印证。同时从图6（b）中可以看出，尽管引入了时间T参数，但由于未做映射处理，导致了分类结果的误判。

综上所述，SE参数具有良好的性能退化指示能力，结合CT参数和有效值，能够构成科学的退化特征向量。结合GG聚类算法良好的聚类性能，能够科学地识别性能退化状态。

4 结论

本文提出了一种基于SE和CT特征的性能退化GG聚类方法，通过实例数据的分析验证，得到如下结论：①SE参数能够反映信号中不规则成分的比例，有效描述性能退化过程中的规律性，并且对复杂度变化十分敏感，计算速度快，对实例信号的分析验证了该方法的有效性；②引入的CT参数能够反映采样数据的时间特征，并且通过对指数函数的映射操作使其更符合机械设备的性能退化规律；③GG聚类方法能够对任意形状的数据进行聚类，将时间约束加入到特征向量中，能够在保持聚类精度的同时，提高类别内部的时间聚集度。所提出的序列离散度指标参数较好地反映出了聚类的时间聚集效果。