某煤矿深部地应力测量及巷道围岩应力场分布规律

2020-04-13熊锋

铁道勘察 2020年2期

熊锋

(中铁大桥勘测设计院集团有限公司，湖北武汉 430050)

1 概述

近年来，我国煤矿开采逐渐由浅部转入深部。随着开采深度的增大，一系列工程灾害也随之而来：如巷道变形加大、采场失稳加剧、岩爆与冲击地压剧增等[1]。“三高与时间效应”(地应力高、温度高、渗透压高及较强的时间效应)使得深部岩体的组织结构、基本行为特征和工程响应均发生了根本性的变化，也是导致深部开采中灾变事故发生的根本原因[2]。因此，了解深部巷道的地应力特征及巷道围岩的应力分布规律是实现巷道围岩稳定与施工安全控制的必要条件之一。

由于地应力的存在，地壳受压会产生缓慢的流变，但仍处于应力平衡状态。然而，巷道开挖意味着卸荷，破坏了地壳内原有的地应力平衡状态，使得一定范围内巷道围岩的初始应力场发生了改变。在这个影响范围之内，巷道垂直应力增大，围岩将产生回弹；超过这个范围，巷道垂直应力仍保持原有的应力状态。根据弹性力学理论，对于圆形巷道，其影响范围约为3倍洞径。如果考虑到开挖扰动效应、应力集中效应以及相邻巷道的影响，应力的调整范围则可能进一步扩大，且调整范围从理论上来说是不确定的，需要通过现场的地应力测试来确定。因此，了解巷道围岩应力的调整范围及其分布规律至关重要，对支护方案的选择及支护参数的优化具有重要的工程意义。

目前，地应力测试的方法有很多种，根据测量原理的不同，可以分为直接法和间接法两大类[3-4]。直接测量方法中广泛使用的是水压致裂法[5-8]。蔡美峰等应用水压致裂法对玲珑金矿深部地应力进行测量，得到矿区应力场的分布规律；刘允芳采用水压致裂法对单孔中的三维应力进行测量，得到了相关的应力数据。水压致裂法对环境的要求相对比较宽松，能测量地下较深处的绝对应力状态，且无需了解和测定岩石的弹性模量，具有测量空间范围大、受局部影响小、成功率高等优点[9]。间接测量中广泛使用的是应力解除法，其发展历程较长，技术比较成熟[10-11]，如刘允芳等采用应力解除法对空心包体式钻孔的地应力进行测量，得到钻孔的三向应力应变数据。

以下采用水压致裂法，对某煤矿-790 m高程深部巷道进行地应力测试，研究深部巷道的原岩应力和巷道围岩的地应力分布规律。

2 工程概况

该煤矿可采煤为15层，煤层总厚度为31.7 m，分-530 m和-800 m两个面水平开采，现正向第二水平面开拓延深伸。

为保证地应力测试的顺利进行，选择高程为-790 m的东翼矸石胶带机大巷(实际高程为-773.8 m)作为试验巷道，测试地点距联络巷约60 m(如图1所示)。在胶带机大巷附近还有轨道大巷(实际高程为-792.8 m)，两条巷道的水平距离约为75 m，垂直距离约为19 m(如图2所示)。轨道大巷位于中细砂岩层中，胶带机大巷位于泥岩、粉细砂岩层中，周围没有大的断裂构造带通过。

图1 地应力测试地点

图2 相邻巷道布置(单位：m)

3 地应力测试

3.1 测试方案

图3 地应力测试孔及测点布置(单位：m)

采用水压致裂法进行地应力测试。水压致裂法一般可分为平面应力测量和三维应力测量[9]，本项目采用平面应力测量。在巷道的两帮及底板布置了3个测试孔(如图3所示)。其中，1号、3号测试孔为水平孔，孔径110 mm，孔深25 m，均从孔深4.4 m处开始测量，然后每隔3 m测量一次，每孔测量7次；2号为垂直孔，孔径为110 m m，孔深25 m，采用取芯钻进行钻孔，并对取得的岩芯进行抗压强度测试，以查明巷道围岩的基本力学性质。

3.2 测试结果

水压致裂法测试过程中，部分测量压力曲线如图4所示，分别显示了1号孔7.4 m处、2号孔22 m处及3号孔7.4 m处压力曲线随时间的变化情况。根据试验曲线，可以得到破裂压力、重张压力及关闭压力，进而根据水压致裂法平面应力测量的基本假定及计算公式[7]，可以得到最小水平主应力及最大水平主应力(如表1、表2及表3所示)。

其中，D表示孔深，Pb表示破裂压力，Pr表示重张压力，Ps表示关闭压力，σH表示最大水平主应力，σh表示最小水平主应力，σV表示自重应力。

图4 1号孔、2号孔、3号孔地应力测量压力曲线

表1 1号孔地应力测试结果

表2 2号孔地应力测试结果

表3 3号孔地应力测试结果

4 地应力特征及相邻巷道影响

4.1 地应力特征

地应力测量结果表明，煤矿-790 m高程地应力具有如下特征。

(1) 地应力大

由表2可以看出：2号孔最大水平主应力为28.33 MPa，最小水平主应力为16.33 MPa。在钻孔过程中，对3个孔的岩芯进行了单轴抗压强度测试(如表4所示)，其平均抗压强度为164.8 MPa,Rc/σmax=164.8/28.33=5.8,根据规范[12]可知，Rσmax在4～7范围内为高应力。故煤矿-790 m高程处为高应力区。

表4 岩样的单轴抗压强度

(2)原岩应力场以水平构造应力为主

3号孔受邻近巷道(-790 m底板轨道大巷)影响较大，故只考虑1号、2号测试孔的原岩应力测试结果。由表1及表2可知：1号孔22.4 m处侧压力系数(λ=σH/σV)为1.69，2号孔的侧压力系数(λ=σH/σV)为1.63，两处的测试结果较为接近，表明煤矿-790 m高程原岩应力场以水平构造应力为主。

(3)巷道两帮的应力分布具有规律性

由图5及图6可知，在巷道开挖之前，地壳处于地应力平衡状态，其内部的初始应力状态如图5中的应力圆①。在开挖过程中，巷道围岩受到扰动，导致围岩产生了一定的损伤，降低了围岩的承载能力[13-15]。

开挖之后到支护之前，此时巷道洞壁处的水平应力为0，垂直应力加大，巷道围岩的应力状态如图5中的应力圆②，垂直应力沿洞深的分布情况如图6中的分布曲线①。然而，这种状态是不稳定的，随着应力的调整和传递，围岩产生回弹，巷道两帮将产生向内的收缩变形，靠近洞壁处的垂直应力也会迅速下降，此时洞壁处的应力状态迅速由图5中的应力圆②下降为应力圆③，垂直应力沿洞深的分布也由图6中的分布曲线①转变为分布曲线②。实际上，在上述的应力调整过程中，巷道围岩的力学性质也在不断变化，一方面由于开挖扰动的影响，巷道围岩的力学性质出现了一定程度的下降，导致其承载能力降低；另一方面，由于应力集中，靠近洞壁处的围岩进入塑性区，也在一定程度上降低了围岩的承载力。此外，如果考虑流变因素，即随着时间的增长，围岩的强度不断降低，最终达到稳定强度，洞壁的应力状态也由图5中的应力圆③下降为应力圆④，垂直应力沿洞深的分布也由图6中的分布曲线②转变为分布曲线④。开挖扰动、应力集中及长期强度的影响都会导致围岩的应力逐渐转移，但出现的阶段不同。

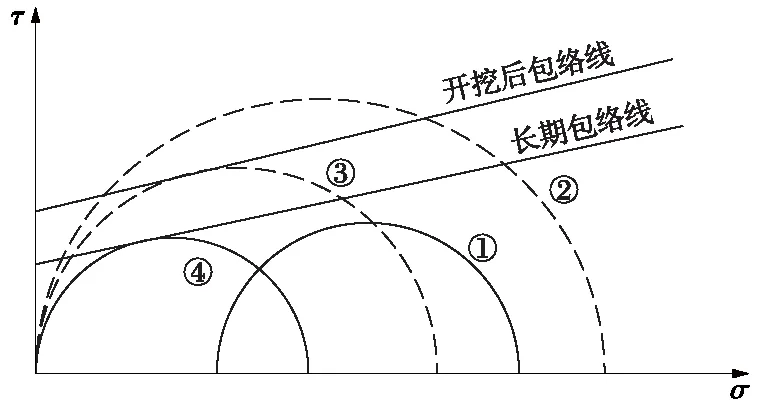
图5 开挖前后帮部围岩的应力圆

图6 开挖后帮部围岩的应力状态变化

将表1及表3中最大主应力及最小主应力的测试结果表示成随深度分布的形式(如图7所示)。由图7可知，1号孔的最大、最小主应力从4.4 m处开始增加，在10.4 m处达到最大值，然后逐渐减小并趋于稳定；3号孔的最大、最小主应力从4.4 m处开始增加，在13.4 m处达到最大值，然后逐渐减小。受测试深度的限制，并没有得到最终的稳定值。比较图7和图6中曲线④的分布规律可以发现，它们的规律基本一致，说明理论分析与测试结果相符。另外，根据图5的应力圆可知，巷道围岩的承载能力在靠近洞壁处最差，距离洞壁越远，承载能力越强，最终趋于一个定值。

图7 巷道围岩两帮主应力分布

4.2 邻近巷道影响

若不考虑左侧邻近巷道(底板轨道大巷)对胶带机大巷的影响，巷道两帮测试孔1号和3号的应力分布在测试误差的范围内应该比较接近。然而，比较图7中巷道左右两帮的应力分布可以发现，受邻近巷道的影响，一侧的巷道帮部应力分布具有以下几个方面的特点。

(1)应力调整范围扩大

未受邻近巷道影响的1号测试孔在约2倍洞径处主应力达到最大值，而受到邻近巷道影响的3号测试孔则在约2.5倍洞径处主应力达到最大值，说明受到邻近巷道的影响，最大主应力向更深处转移(应力的调整范围扩大了)。另外，1号测试孔的主应力达到最大值后很快趋于一个稳定值，而3号测试孔的应力在同样的深度却依然未达到一个稳定值，这也说明3号测试孔应力调整的范围超过了1号测试孔。

(2)主应力值降低

对于相同的孔深，3号测试孔的主应力均小于1号测试孔，说明随着应力调整范围的扩大，对应主应力值降低。

(3)构造应力和应力集中程度降低

由表1和表3可知，3号测试孔中的侧压力系数要小于1号测试孔，说明受邻近巷道的影响，巷道的构造应力下降，应力集中程度降低。