中国股市是宏观经济的晴雨表吗？——基于马氏域变模型的研究

孟庆斌，张永冀，汪昌云

(1.中国人民大学商学院，北京 100872；2.北京理工大学管理与经济学院，北京 100081)

1 引言

我国股市经历了将近30年的发展，市值规模迅速扩大，资金配置效率逐步提升，在社会经济融资体系中发挥了越来越重要的作用。在这种趋势下，证券市场作为我国实体经济“晴雨表”的作用日益明显，对实体经济和宏观政策变动的反应也越来越灵敏。相应地，宏观经济因素对股市的影响也逐渐成为我国经济政策制定过程中需考虑的重要因素之一。因此，我们有必要结合股市的发展变化，考察和比较不同阶段我国宏观经济因素对股市的影响，从而为政策制定提供参考依据。

证券价格会对宏、微观信息及时作出反应。以往研究多从微观角度探讨价格波动机制[1-2]。近年来宏观经济因素对股市波动的影响日益得到学术界广泛关注。国内外研究主要从三个方面研究宏观经济因素对股市的影响：首先是经济增长对股市的影响，如Schwert[3]对美国股市波动与美国宏观经济、金融政策波动之间的相关性进行了研究；Beltrattia和Morana[4]考察了美国股市周期和宏观经济周期之间的协同性。郑江淮等[5]、许均华和李启亚[6]、梁琪和腾建州[7]、刘少波和丁菊红[8]、唐平和刘燕[9]、余秋玲和朱宏泉[10]、赵华和秦可佶[11]等国内学者从不同角度探讨了我国经济增长与股市之间的联系，探讨了实体经济发展中证券市场的功能定位问题。其次是货币政策对股市的影响，如Thorbecke[12]研究发现美国货币政策(利率或联邦准备金)对股市收益有显著影响。中国人民银行研究局课题组[13]、孙华妤和马跃[14]、吕江林[15]等分别从货币政策的制定、调整等角度分析了货币政策与股市的关系，基于证券市场反应对货币政策的制定和实施提出建议。此外，还有不少学者关注国际资金流动对股市的影响，如Bollerslv等[16]从理论上对政策变动对股价跳跃的影响进行建模，给出了解决此类问题的一般理论框架。Jorion[17]研究发现美元汇率波动对美国股市影响并不显著。吕江林等[18]、杨海珍等[19]研究了人民币升值引起的资金流入对中国股市的影响。

已有研究为我们深入理解宏观经济因素对股市影响提供了很好的借鉴，但在这些文献中仍然存在两方面的问题：首先，这些文献大多侧重于分析特定经济变量对股市的影响，虽具有较强的针对性，但由于缺少对这些变量影响程度的综合分析，使我们难以从总体上对各种经济变量对股市的影响进行分析和比较。同时，现有文献多在线性模型框架下研究经济变量对股市的影响，对不同时间样本进行计量检验时得到的结论往往相差较大。造成该结果的原因在于，很多经济变量的波动具有很强的周期性或者说非线性性，线性模型的假设势必与现实情况相去甚远。针对以上问题，本文将选取反映经济增长和货币政策的主要宏观变量，利用能够捕捉经济变量之间非线性关系的计量方法——马氏域变向量自回归模型(Markov Switching Vector Autoregressive)，建立统一的计量模型框架，分析其对股市的综合影响。

2 股市收益与宏观经济变量的马氏域变特征

本章将利用马氏域变模型对我国股市收益及各宏观经济变量进行建模，分析其周期性波动特征，检验其在不同时期所处状态，并在此基础上对各宏观经济变量与股市之间的关系进行分析。

2.1 数据处理及统计分析

本文以上证综合指数的变动反映股市收益，选取反映产出、价格和货币方面的宏观经济指标，如：工业增加值、出口、消费(由于居民消费数据无法获得，文中以社会消费品零售总额代表消费数据)、通货膨胀率、利率、广义货币以及人民币兑美元实际汇率等。投资也是反映实体经济增长的重要变量，但由于缺乏完整的月度数据，因此并未纳入本文。数据样本期为从1996年1月到2015年12月(由于本文研究的多个经济变量序列中，最短的序列从1996年1月开始，因此我们的样本期初始点设定为此时)，采用月度数据，数据来源于万德资讯数据库和中经网数据库。

在数据处理上：股市收益率(dsit)是通过对月末上证指数取对数后进行差分获得。产出方面，由于官方公布的GDP为季度序列数据，故本文用工业增加值进行替代，先对其进行X-12-ARIMA季节调整，然后进行对数变换并做差分，就得到了工业增加值增长率(dyt)。利用同样方法，计算得到出口增长率 (dext)、消费增长率(dct)、月度环比通货膨胀率(inft)。对银行间七日同业拆借利率、广义货币、人民币兑美元实际汇率进行对数变换并取差分，可得利率变化率(dintt)、广义货币变化率(dM2t)和人民币兑美元实际汇率变化率(dret)。各序列的统计特征见表1。

表1 宏观经济变量与股市收益率基本统计特征(1996年1月-2015年12月)

注： 1.*、**、***分别表示在10%、5%、1%的水平上显著；2.JB(Jarque-Bera)统计量检验样本是否服从正态分布；3.Q(8)(Ljung-Box)统计量检验时间序列中是否存在序列相关性；4.ADF(Augmented Dickey-Fuller)统计量检验各序列中是否存在单位根。

表1显示，各序列JB统计量均较大，说明其峰度和偏度较高、波动剧烈、分布均呈非正态性；Q(8)统计量表明序列存在较为严重的序列相关性；ADF统计量均在1%水平上显著，说明序列平稳。综合判断这八个宏观因素序列呈非线性性，即可能存在着某种结构性变化或结构性断点，为下文利用马氏域变模型对各序列进行分析和研究提供了依据。

2.2 模型设定与参数估计

马氏域变模型最早由Quandt[20]提出，后经Goldfeld和Quandt[21]逐步完善，多用于非线性计量问题研究。虽然马氏域变模型在上世纪50年代末期就已提出，但在几近30年之后，随着计算机信息技术的发展与普及，才被广泛应用于实证金融研究当中。Hamilton[22-24]、Cecchetti等[26]、杨继平和张春会[26]等应用此模型预测利率、国民生产总值、汇率以及证券收益率与波动率等，均表现为很高的预测准确性。因此，本文先对上证指数收益率建立马氏域变自回归模型；然后，将工业增加值、消费以及出口三变量联合起来，建立马氏域变向量自回归模型，以分析实体经济周期；对于反映价格和货币政策的变量通货膨胀率、实际汇率、广义货币和利率，则分别建立马氏域变自回归模型。需要指出的是，马氏域变自回归模型是马氏域变向量自回归模型变量数为一时的特殊情况。

p阶马氏域变向量自回归模型的一般形式可表示为：

(1)

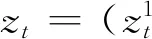
P(St=0|St-1=0)=p00,P(St=1|St-1=0)=p01

P(St=0|St-1=1)=p10,P(St=1|St-1=1)=p11

(2)

其中，p00、p01、p10和p11为正常数，满足p00+p01=p10+p11=1。进一步，可以将(1)式改写为均值调整形式，即：

(3)

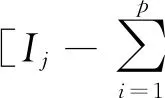
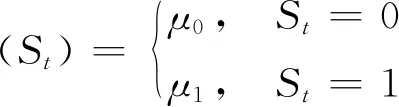
(4)

(4)式说明，随着经济形势在(0,1)之间转换，各宏观经济变量的均值也在μ0和μ1之间变化。当向量zt仅包含一个宏观经济变量时，模型(3)易化为马氏域变自回归模型。

常见有两种马氏域变向量自回归模型的参数估计方法：吉布斯采样法(Gibbs Sampling)和最大似然估计法。吉布斯采样法采用马氏链蒙特卡洛迭代模拟技术(MCMC)，属于贝叶斯分析的范畴，可提供相对丰富的信息，如参数后验分布信息。当模型待估参数较多、估算较复杂时，吉布斯采样法更为准确和高效。最大似然估计法属于经典回归估计法，通过卡尔曼滤波(The Kalman Filtering)进行预测方差分解，得到模型参数的最大似然估计。当模型待估参数较少、估算较为简单时，最大似然估计法更为方便和快捷。由于本文模型中待估参数相对较少，样本期间较短，因此选用最大似然估计法。

本文对上述变量分别建立了MSM-VAR、MSM-AR、MSMH-AR、三类马氏域变向量自回归模型。在实体经济发展过程中，政府会通过财政政策、货币政策等一篮子工具调节市场，促进经济平稳增长，避免经济增速剧烈波动。MSM-VAR模型适用于均值随经济状态转换而变化，而自回归系数与随机扰动项协方差矩阵都不受状态转换影响的情形。因此本文采用MSM-VAR模型对实体经济增长建模，所涉及的经济变量有工业增加值增长率、消费增长率和出口增长率，此时(3)式中的zt=(dyt,dct,ext)’。MSM-AR为仅包含单个变量的MSM-VAR模型。由于通货膨胀率、广义货币、实际汇率在短期内极少出现剧烈波动，其变动率的状态转移特征主要表现为均值的变化，因此本文利用MSM-VAR模型来表征通货膨胀率、广义货币和实际汇率变化率的状态转移特征，zt分别等于inft、dM2t和dret。股市收益和利率的波动相较其他经济变量更为剧烈，而MSMH-AR模型是除均值外，扰动项方差也随状态转移而变化的MSM-VAR模型，因此可利用该模型对股市收益和利率建模，zt分别等于dsit和dintt。以上各模型的自回归阶数均依据AIC准则获得，模型参数估计结果见表2。

从表2中可以看出，各序列残差和残差平方的Ljung-Box Q统计量均接受了残差中不含序列相关性的假设。根据马氏域变向量自回归模型和经典线性模型的对数似然值，本文构造出似然比统计量，对经济状态转移前后模型的拟合效果进行比对检验。其中，对反映实体经济增长的工业增加值增长率、消费增长率和出口增长率建立的MSM-VAR模型相较于经典VAR模型构成的似然比统计量为LRdyt,dct,dext=18>χ0.01(3)=11.34；对通货膨胀率、广义货币和实际汇率变化率所建立的MSM-AR模型相较于AR模型的似然比统计量分别为LRinft=10、LRdM2t=116和LRdret=21，均大于χ0.01(1)=6.63；对股市收益率、利率所建立的MSMH-AR模型相较于经典AR模型的似然比统计量分别为LRdsit=34和LRintt=180，两者均大于χ0.01(2)=9.21。综上可以看出，引入状态转移后，模型的拟合效果显著提高，进一步说明利用马氏域变向量模型对各变量进行建模是适合的。

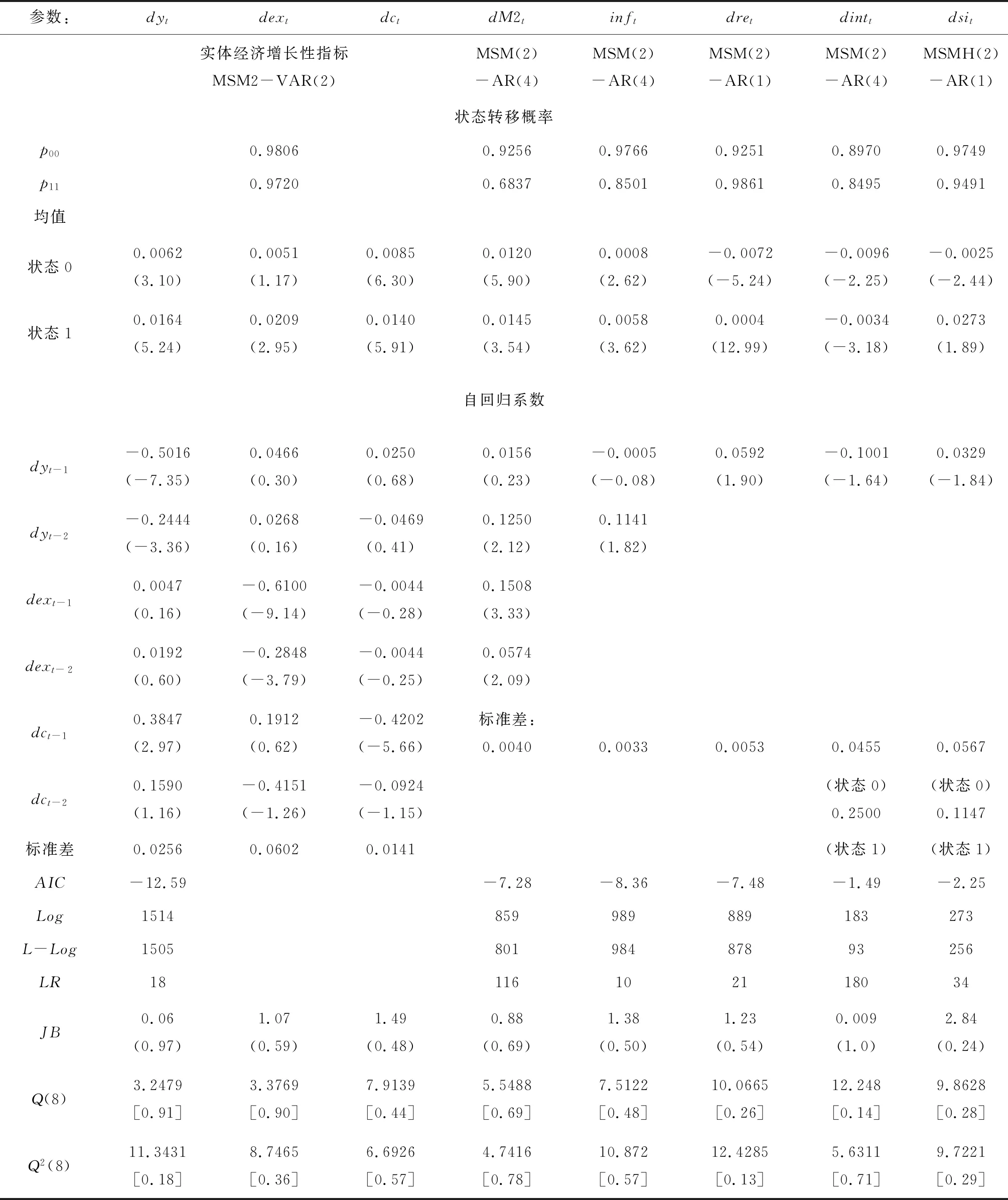
表2 上证综指收益率及宏观经济变量的马氏域变向量自回归参数估计结果

注：1.Q(8)和Q2(8)统计量检验时间序列中是否存在序列相关性；2.Q(8)和Q2(8)统计量下方中括号内数据为p值，其他数据下小括号内数据为参数估计值的t统计量；3.Log表示马氏域变向量自回归模型参数估计的对数似然值、L-Log表示经典线性模型参数估计的对数似然值。

各变量在样本期内不同阶段处于某一状态的概率见图1到图6，分别表示股市高收益率状态概率、工业增加值高增长状态概率、广义货币高增长状态概率、高通货膨胀率状态概率、利率高波动率状态概率以及实际汇率下降(人民币升值)状态概率等。

图1 股市高收益率状态概率

图2 工业增加值高增长状态概率

图3 广义货币高增长状态概率

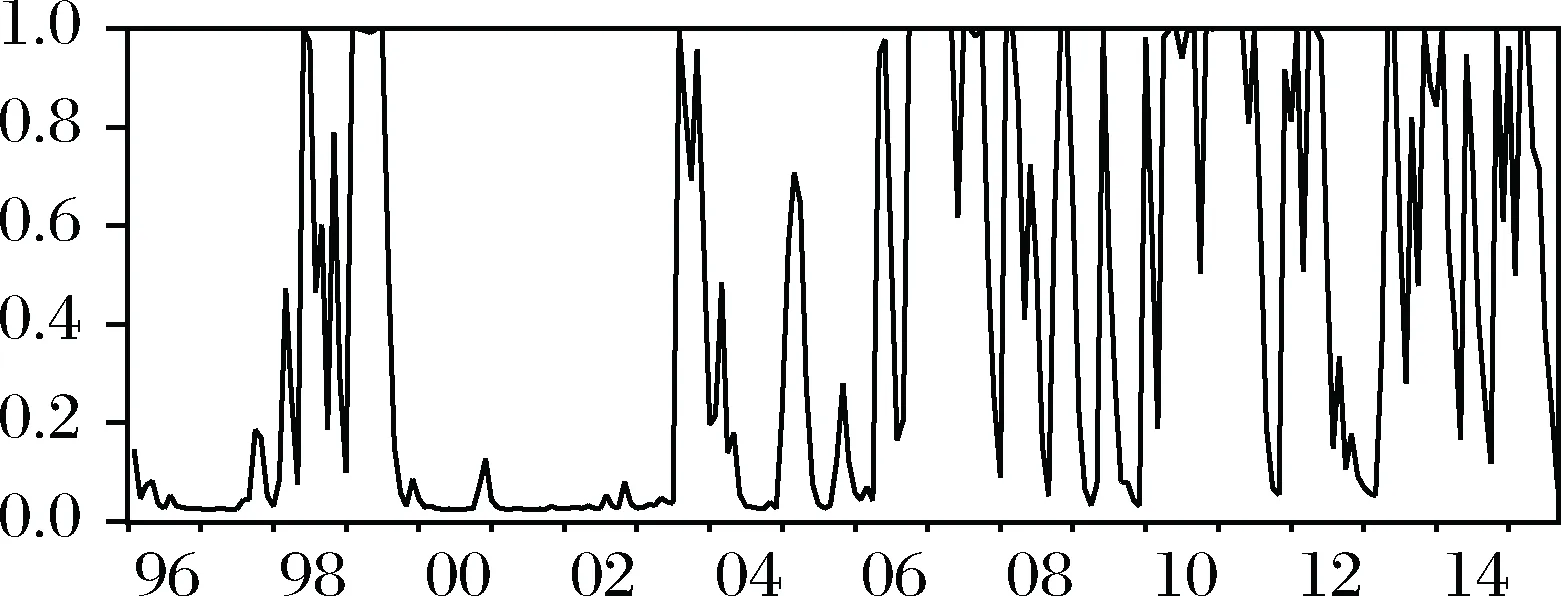
图4 利率高波动状态概率

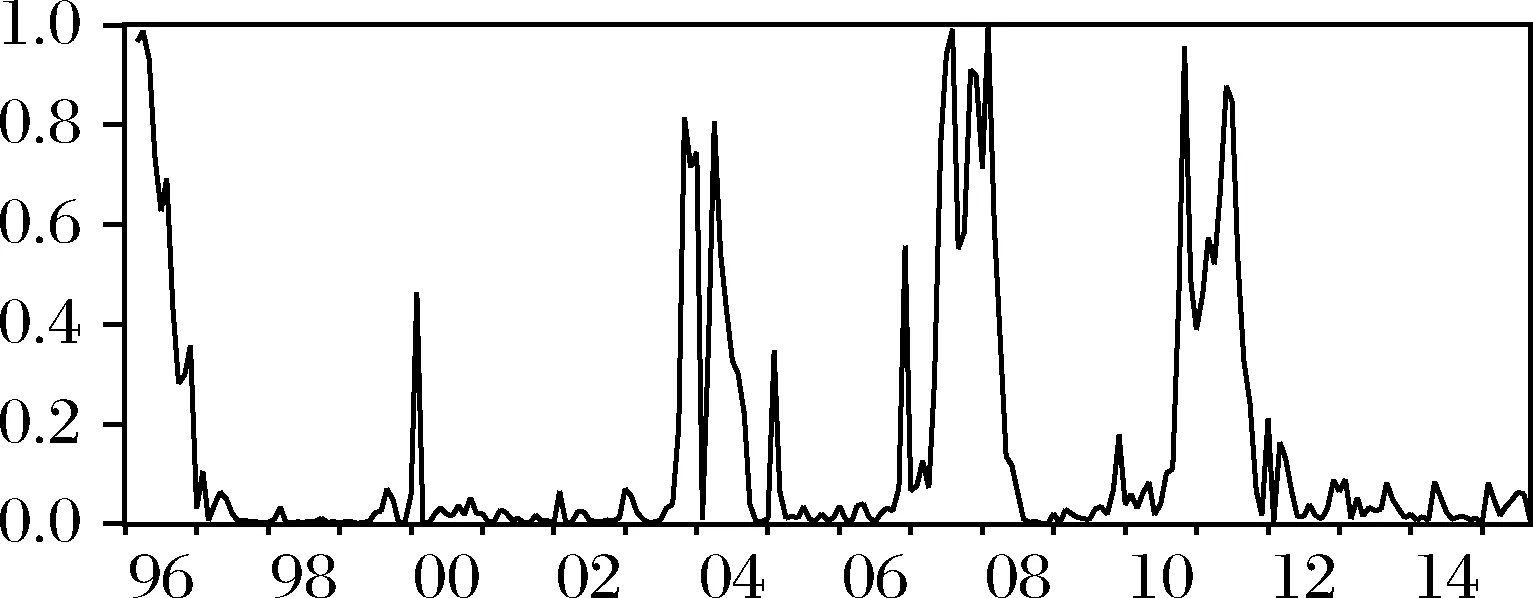
图5 高通货膨胀状态概率

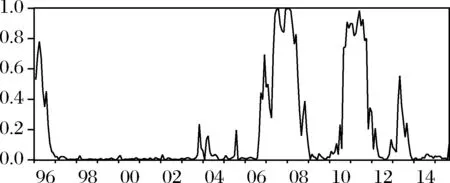
图6 实际汇率下降状态概率

2.3 状态转换特征分析

根据表2中的模型参数估计结果和图1到图6中的概率结果可以看出：股票市场在低收益率状态(St=0，下称“熊市”)和高收益率状态(St=1，下称“牛市”)下的均值分别为-0.0025和0.0273，波动率分别为0.0567和0.1147，差距明显。牛市在相邻时间点之间得以维持的概率为97.49%，意味着其平均持续期达到将近39.8个月；熊市在相邻时间点之间得以维持的概率为94.91%，说明其平均持续期约为19.6个月，为牛市平均持续期的一半。从图1中可以看到，我国股市在1996年到1997年4月间处于牛市，之后受1997年亚洲金融危机冲击，迅速由牛转熊，虽然在1999年的个别月份出现了强劲反弹，但很快又重陷低迷，这样的状态一直持续到2006年；从2006年5月到2009年2月，我国股市迅速完成了一轮大涨大跌的周期，先是在2006年5月开始到2007年10月的一年半时间里迅速上涨超过6倍，接着从2007年11月到2008年10月，又下跌了将近75%；从2008年12月开始，我国股市开始反弹，并一直持续到2009年10月，此后又进入了长达5年的持续震荡下行状态； 2014年10月，我国股市经历了新一轮的大幅快速上涨，并一直延续到本文样本期的结束(2015年9月)。

就实体经济而言，高增速(St=1)和低增速(St=0)时工业增加值增长率、出口增长率和消费增长率的均值差距明显，分别为0.0164、0.0209、0.0140和0.0062、0.0051、0.0085。经济低增速期在相邻时点间维持的概率为98.06%，平均持续期为51.5个月。经济高增速时期在相邻时点间维持的概率为97.2%，平均持续期为35.7个月，略小于低增速期。在所考察的样本期内，实体经济处于低增速状态的时期主要有三个阶段：第一个阶段为1997年到2001年。在此期间，从1996年开始，实体经济增速逐渐下滑并进入收缩状态，这种状态一直持续到1999年6月，在1999年7月到2000年之间虽然有所回暖，但2001年又出现反复，直到2002年才彻底复苏，进入了较为持续和稳定的扩张期。第二个阶段为从2008年9月到2009年5月，该阶段，受金融危机冲击，我国实体经济迅速陷入收缩期，但在财政货币政策的双重刺激下，不到半年时间实体经济便走出低谷。第三个阶段为2012年之后直到2015年9月，其原因主要是由于我国发展模式的“减速换挡”，以及同期欧美经济的持续低迷。

广义货币高低增长率状态下的均值分别为0.0145和0.0120。低增长时期(St=0)，相邻时点间得以维持的概率为92.56%，平均持续期将近13.4个月，显著高于高增长时期(St=1)68.37%的维持概率和3.2个月的平均持续期。M2高速增长的时段分别是1996年、2001年、2008年到2009年7月、2011年和2015年。其中第一个时期是延续1994年高通胀时期的资金大量投放，而后几个时期则是我国为应对危机和经济下滑实行宽松货币政策的结果。

利率在两状态下的均值分别为-0.0096和-0.0034，差距比较明显，但二者波动率差距更大，高状态(St=1)下波动率接近低状态(St=0)下的5.5倍。两状态维持概率也很接近，低状态在相邻时点间的维持状态不变的概率为89.70%，平均持续期为9.7个月，高状态在相邻时点间的维持状态不变的概率为84.95%，平均持续期约为6.6个月。从图4可以看出，1998年到1999年和2003年到2015年两个区间利率波动较剧烈，前一时期政府利用货币工具刺激经济频繁降息，2008年是后一时期的分水岭，当年8月份之前，政府为防止经济过热和高通胀而多次加息，8月份之后，央行为应对美国金融危机对中国的冲击而连续降息。

高低状态下的通货膨胀率均值分别为0.0058和0.0008。低通胀状态(St=0)相邻时点间得以维持的概率为97.66%，平均持续期为42.7个月，显著高于高通胀状态(St=1)下85.01%的维持概率以及6.7个月的平均持续期。从图5中可以看到，在所研究的时间段内，我国通胀情况大致可以分为四个阶段：从1996年到2003年间，我国通胀率长期处于较低的水平，只有1997年和2000年里的个别月份(2007年4月和2000年2月)出现了短期上升；2003年后，中国经济逐渐进入高增长时期，高通胀现象出现频率和持续时间均显著增加，尤其是2003年10月到2004年4月和 2007年5月到2008年4月这两个阶段，通胀率始终都维持在较高水平；2008年下半年，抑制通胀的紧缩货币政策开始逐渐发挥作用，同时受全球金融危机影响，实体经济迅速下滑，通货紧缩随之而来；进入2010年之后，在我国经济复苏、全球大宗商品价格上扬的推动下，通货膨胀水平再次快速攀升，至当年10月，高通胀概率已超过70%，这种状况一直持续到2011年底。

实际汇率在下降状态(人民币升值，St=0)下的平均下降速度为-0.0072，在上升状态(人民币贬值St=1)下以每月0.0004的速度缓慢上升。下降状态中相邻时点间维持概率为92.51%，平均持续期为1.33个月，远低于上升状态相邻时点间98.61%的维持概率和71.9个月的平均持续期。从图6中可以看出，人民币升值主要集中在1996年3到6月、2006年9月到2008年6月以及2010年7月到2011年10月这三个阶段。

将图1分别与图2至图6进行对比可以看出：首先，大部分时间里股市和实体经济保持了较好的协同性，股市周期略领先于实体经济周期，这说明股市是实体经济的晴雨表，实体经济是股市的源动力。在2002年到2005年间，实体经济和股市的协同性关系遭到破坏，实体经济已走出低谷，实现高速增长，而股市却依然低迷。造成这一结果的主要原因除了货币当局在该阶段提高利率对股市产生的抑制作用外，更重要的是国有股减持政策迟迟未能公布，市场扩容前景极不明朗，导致市场情绪长期低迷。第二，M2的快速增加之后往往伴随着股市的大幅增长，但股市大幅上涨并不与M2的快速增加相伴，且股市的长期变化与M2的存量结构之间没有关系，这说明阶段性的货币供给增加会在一定程度上推动股市上涨，但不会将股市维持在一定的水平。第三，利率调节无法对证券市场产生立竿见影的影响，其效果具有一定的滞后性。作为常见的央行货币政策，利率调节是对未来经济趋势的提前干预，除非是市场预期之外的调节，不然股价有可能已经反应了货币政策的变化。第四，通货膨胀因素对股市收益率影响显著，通胀率的上扬短期会对股价上涨产生较大的刺激，但长期影响会比较复杂。第五，实际汇率变化周期与股市收益率周期相协调，尤其是从2004年以后，实际汇率下降阶段与股市高涨阶段高度吻合，这从实证上说明了汇率变动与股市变动联系密切，并且随着我国开放程度和汇率市场化程度的不断加深而加强。这是因为，在两国价格水平短期相对稳定的状态下，人民币实际汇率下降对应着名义汇率上人民币升值，这会使人们产生强烈的资金流入预期，从而刺激股市上涨。

3 宏观经济波动对股市影响的实证检验

上一部分对我国股市收益率和各宏观经济变量的周期性特征进行了研究，同时分析了各变量与股市之间的相互联系。在此基础上，本部分将利用马氏域变向量自回归模型研究宏观经济波动对股市的影响。

3.1 模型设定及参数估计结果

首先从各变量中剔除趋势性成分，得到其绝对离差，然后利用MSMH-VAR模型(均值和标准差都随着状态的变化而变化的马氏域变向量自回归模型)对绝对离差进行建模，最后将通过MSMH-VAR模型的冲击响应函数来分析各宏观经济因素对股市的影响。需要指出的是，剔除了变量趋势性成分后所得的冲击响应函数，度量的是各变量偏离趋势的超额波动所引起的股市偏离趋势的超额收益。

工业增加值增长率、出口增长率、消费增长率、广义货币增长率、通货膨胀率、利率变化率、人民币兑美元实际汇率变化率和股市收益率的绝对离差分别记为：Dyt、Dext、Dct、DM2t、Dintt、Dinft、Dret和Dsit，(3)式中的zt就等于(Dyt,Dext,Dct,DM2t,Dintt,Dinft,Dret,Dsit)’。利用AIC确定该模型的滞后阶数为1，进而用最大似然估计法对模型参数进行估计，结果见表3。

从表3可以看出，各变量残差序列和大部分变量残差平方序列的Ljung-Box Q统计量均无法拒绝其不存在序列相关性的假设，这说明模型的设定是合理的。同时，将该模型与不考虑状态转移的经典VAR模型进行似然比对照检验，得到LRMSMH=438>χ0.01(16)=32，在1%的显著性水平下拒绝原假设，说明引入状态转移特征后模型的拟合效果显著提高。除通货膨胀率外，其他变量序列在状态1时的均值显著大于状态0时的均值，各变量标准差的情况类似，表明当经济快速增长时，宏观经济指标波动更为剧烈。从图7可以看出，整个马氏域变向量自回归系统状态转移比单个变量状态转移更加频繁，状态0下相邻时间点间得以维持的概率为89.93%，平均持续期约9.9个月，高于状态1时的77.92%维持概率和约4.5个月的平均持续期。

表3 宏观经济因素对股市收益率影响的MSM(2)-VAR(1)模型参数估计结果

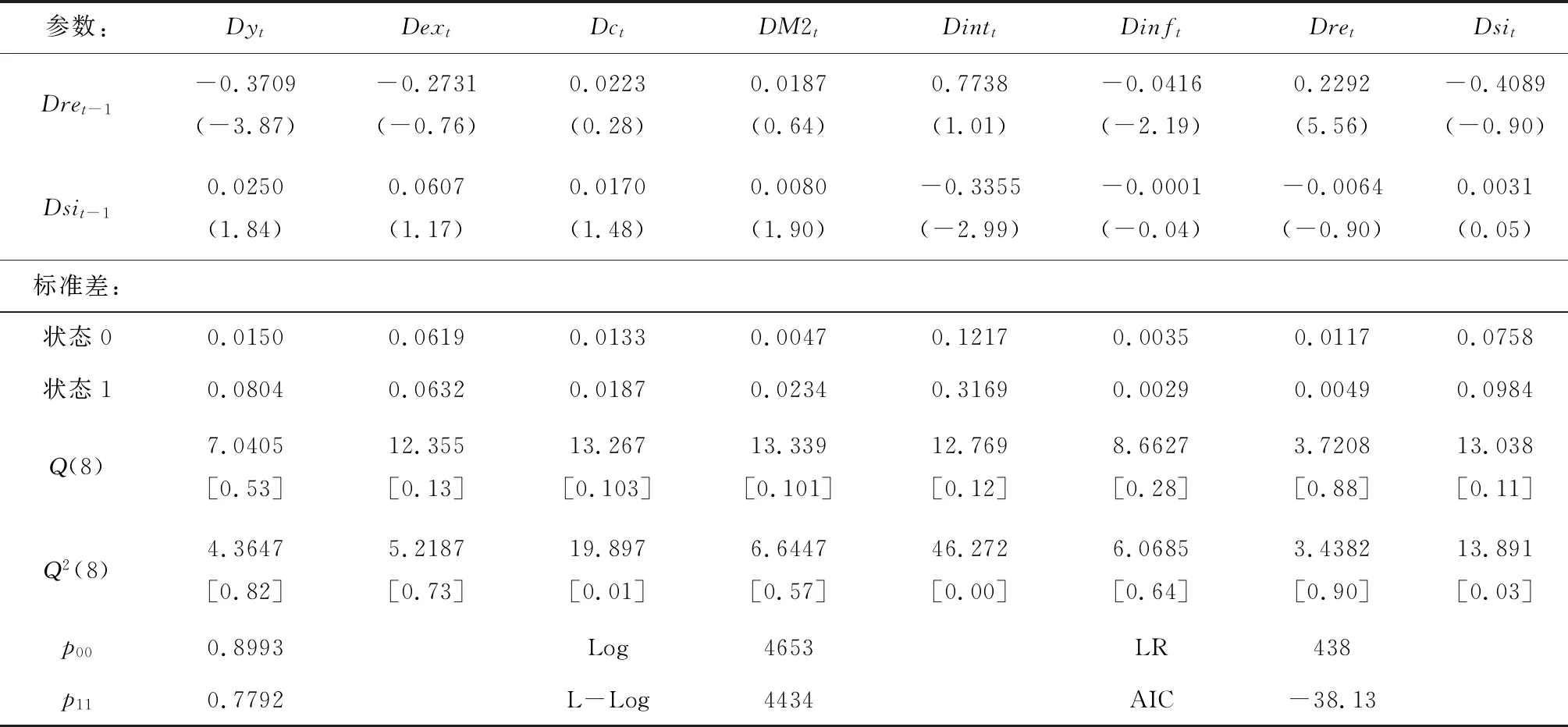
续表3 宏观经济因素对股市收益率影响的MSM(2)-VAR(1)模型参数估计结果

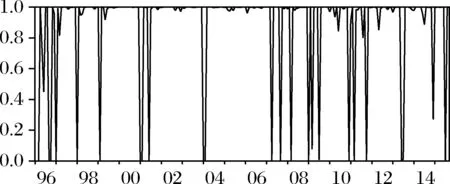
图7 状态0滤波概率

3.2 宏观经济变量对股市收益率的脉冲响应分析

本文进一步将通过估算马氏域变向量自回归模型的脉冲响应函数，来分析宏观经济波动和经济政策调整对股市收益的动态影响。马氏域变向量自回归模型本质上属于非线性计量模型，因此经典的向量自回归模型脉冲响应函数并不适用。Krolzig[27]提出了一种新的脉冲响应函数，具有广义脉冲响应函数的优势，不仅可用来考察非线性动态模型高斯新息的脉冲响应，还可以考察状态转移过程中各变量所受冲击。状态0时的总体滤波概率见图7。宏观经济因素波动对股市收益的脉冲响应函数如图8(a)和图8(b)所示。状态转移过程中各变量所受到的冲击影响见图9(a)和9(b)，两图分别代表各变量在状态1向状态0和状态0向状态1转移过程中受到的冲击。

图8(a)及图8(b)显示：两种状态下，各宏观经济因素对股市收益率的影响在三个月内达到峰值，半年之后基本衰减殆尽，表现出较好的收敛性。在低状态下，人民币实际汇率下降和M2增加对股市收益的影响最大，两者1个标准差的冲击，在下一期分别引起股市收益增加0.013和0.006。同时，人民币实际汇率下降对股市收益的冲击迅速收敛并消失，且持续期短，而M2增加的冲击则体现出更强的震荡特征且持续期较长。通货膨胀和工业增加值对股市收益影响次之，两者1个标准差的冲击分别使下一期的股市收益增加0.003和0.0023，两者对股市冲击响应函数的变化特征也基本相同，相比而言，通货膨胀影响的震荡性略强。利率是唯一对股市收益产生负向冲击的变量，其提高1个标准差可在下一期对股市产生0.0028的负向冲击，此外利率冲击的衰减最为平缓。消费和出口对股市的影响效果相当一致，其增长对股市下一期的影响几乎为零，两期后出现峰值，两者1个标准差的冲击分别使股市收益提高0.0063和0.0054。

图8(a) 宏观经济波动及政策调整对股市收益率的影响(状态0)

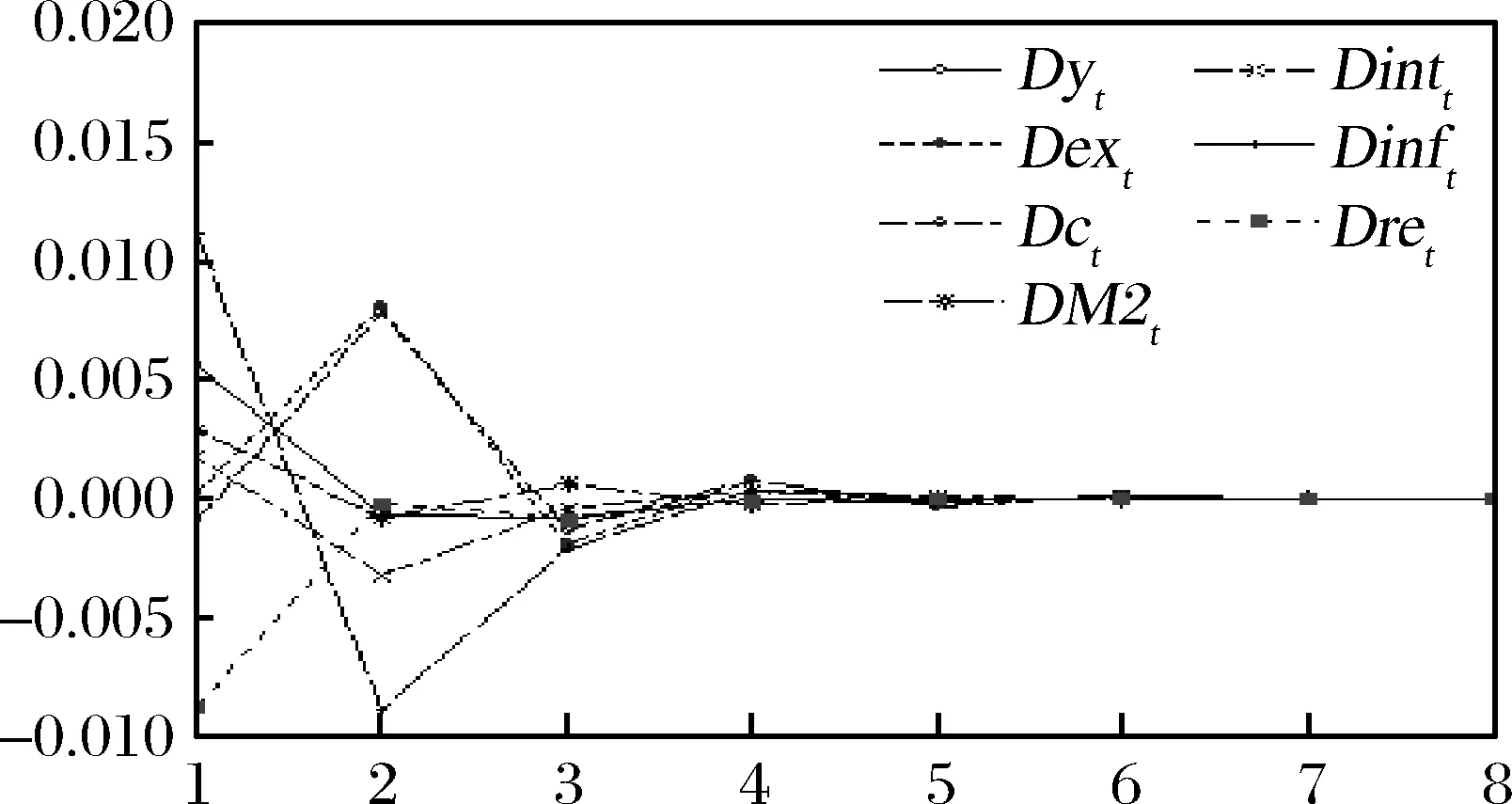
图8(b) 宏观经济波动及政策调整对股市收益率的影响(状态1)

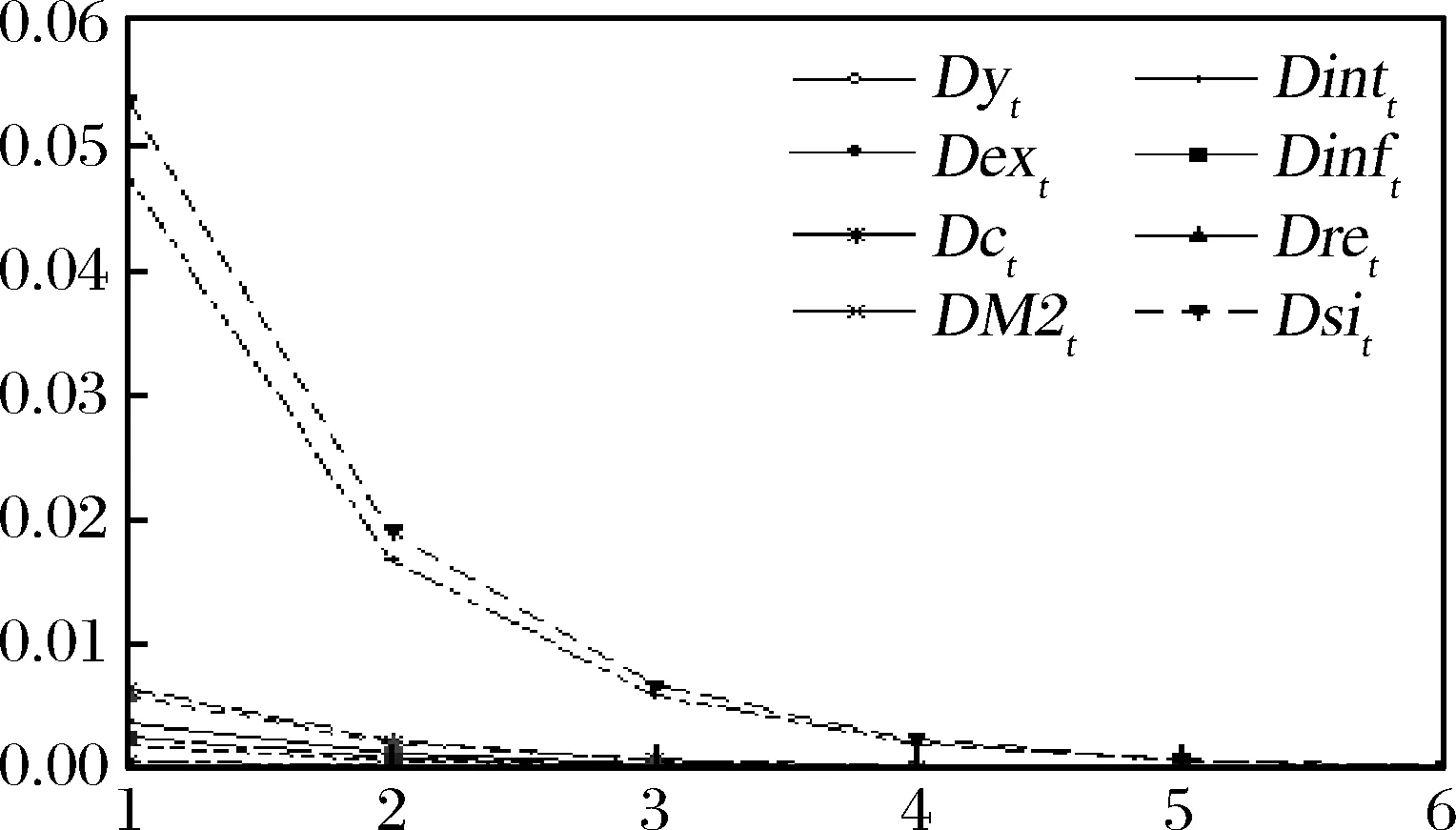
图9(a) 各变量在状态1向状态0转移过程中受到的冲击

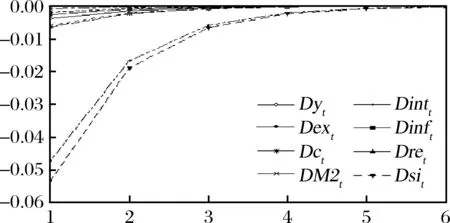
图9(b) 各变量在状态0向状态1转移过程中受到的冲击

在高状态下，通货膨胀对股市收益的影响最大，其1个标准差的冲击可带来股市收益0.011的增加，同时其冲击响应函数的变化形式与低状态下基本相近。人民币实际汇率的冲击响应次之，且几乎是低状态下的等比例缩小，其1个标准差的下降使股市收益在下期提高0.0087个标准差。工业增加值、出口和消费三个变量对股市收益的影响则几乎是低状态下的等比放大，其中工业增加值1个标准差的增加可使股市收益下期增加0.0056，出口和消费每提高1个标准差分别使股市收益在滞后两期出现0.0081和0.0079的增加。高状态下M2对股市收益影响显著低于低状态下的影响，其1个标准差的冲击只能使股市收益在下期增加0.0029。与低状态下相差最大的是利率的影响，在提高利率的下期，股市收益出现了0.0017的提高。

从两状态下冲击响应函数的对比中可以看到：首先，除了利率之外，股市收益对其他变量波动在两状态下冲击响应的方向是相同的，工业增加值、出口、消费和实际汇率在高低状态下对股市的影响非常相近，在高状态下，工业增加值、出口和消费对股市的影响要大一些，说明高状态下实体经济的增长更容易反映在证券市场上，而实际汇率的变动则在低状态下对股市影响更大。其次，M2和通货膨胀在高低两状态下对股市的影响差异很大。M2变动在低状态下对股市的影响极大，说明大量发行货币是刺激股市的有效方法，1999年东南亚金融危机过后股市的大涨以及2008年底金融危机阴霾下我国股市的“V”型反转都与流动性的大量释放有关；通胀在高状态下对股市的影响远远超过低状态下的影响，同时也是高状态下所有变量中对股市影响最大的，说明遏制通胀是抑制股价泡沫较为有效的手段，我国股市在2007年12月的触顶回落就在一定程度上说明了这个问题。最后，虽然利率在两状态下对股市收益的影响都比较小，但其方向在高低状态下却截然相反。其原因在于，在低状态下降低利率可以在一定程度上刺激经济、提振股市；在高状态下，虽然提高利率会对股市形成一定打击，但由于市场对加息的提前预期，这种打压更多的出现在加息之前，而加息的政策落地时，投资者会认为利空已经兑现而买入股票从而推动股市上涨，2007年多次加息当天股市大涨正说明了这个问题。

从图9中可以看出：经济形势在高、低状态之间迁移时，各变量受到的冲击成镜像关系，即在状态变量从0到1和从1到0转换过程中，同一经济变量受到的冲击大小相等、方向相反。因此，不失一般性且为简单起见，我们仅对从高状态向低状态转移情形进行分析。在此情形下，各变量波动水平迅速下降，半年之后状态转换所造成的冲击基本淡化和消失。在该过程中，受到冲击最小的是M2、出口和通胀率，说明央行的干预和调节减缓了目标变量的波动；产出、消费和汇率变化次之，所受冲击较大，这一方面体现出工业产出、消费和汇率对整体经济状态的依赖性较强，另一方面是由于我国工业产出和消费是宏观经济周期的主要决定因素，一旦宏观经济状态发生变动，两者的下降幅度就会比较明显；利率所受到的冲击非常剧烈，这与利率变动较为灵活的特征是分不开的；在状态转移过程中，股市所受到的冲击最大，其下降幅度约为1.89%，这充分说明股市对经济变动的反应最为灵敏，但其中也可能蕴含了超调的风险。

4 结语

本文研究了我国宏观经济因素变动对股市的影响。在研究中，我们选取反映实体经济增长和货币政策变动的产出、价格和货币因素，包括工业增加值、消费、出口、通货膨胀率、M2、利率以及人民币对美元的实际汇率，来考察其对股市收益率的影响。本文首先利用马氏域变模型对我国股市收益率和各宏观经济变量在不同时期所处状态进行识别，进而分析了各宏观经济变量周期与股市周期之间的关系；在此基础上，依据各宏观经济因素对股市收益绝对离差的冲击响应函数探讨了彼此间关系。研究发现：

首先，中国股市收益率和各宏观经济因素变动皆具有明显的非线性，对它们的波动周期进行分析得出：对于反映实体经济增长的因素而言，在大多数时间里实体经济变动和股市波动保持了较好的协同性，股市周期略领先于实体经济周期，这说明股市是实体经济的晴雨表，实体经济是股市的源动力。对于货币政策而言，广义货币的快速增长往往伴随着股市的大幅上涨，但股市大幅上涨阶段并不与广义货币的快速增长相伴，说明货币供给增加会在一定程度上推动股市上涨，但并非股市上涨的主要因素；利率调节无法对股市周期变化产生立竿见影的影响，无论是股市的上升期还是下跌期，其效果的发挥体现出一定的滞后性。央行准备金率的调整也与利率调节情况类似。于价格因素而言，通胀率的上扬往往对股价的短期上涨产生较大的刺激作用，但这种影响会伴随着货币政策的调整而逐渐衰减；实际汇率变化周期与股市收益率周期相协同，尤其是从2005年以后，汇率的上升阶段与股市高涨阶段高度吻合，说明汇率变化与股市变动联系密切，并且随着我国开放程度和汇率市场化程度的不断加深而加强。

其次，利用马氏域变向量自回归模型对宏观经济变量和股市收益的绝对离差进行建模，并分析其冲击响应函数可以发现：第一，除了利率之外，股市收益对其他变量波动在两状态下冲击响应的方向是相同的，尤其是工业增加值、出口、消费和实际汇率在高低状态下对股市的影响非常相近。第二，M2和通货膨胀在高低两状态下它们各自对股市收益的影响差异很大。M2变动在低状态下对股市的影响极大，说明大量发行货币是刺激股市的有效方法；通胀在高状态下对股市的影响远远超过低状态下的影响，说明遏制通胀是抑制股价泡沫较为有效的手段。最后，虽然利率在两状态下对股市收益的影响都比较小，但其方向在高低状态下却截然相反，低状态下降低利率可以在一定程度上提振股市，高状态下，虽然提高利率会对股市形成负面冲击，但由于市场对加息的提前预期，股价下跌更多的出现在加息之前。靴子落地之后，股市反而会迎来上涨。

另外，在从高状态向低状态转移时，受到冲击最小的是消费，表明其对宏观经济状态变化的弹性较小；汇率、通货膨胀率和M2所受冲击较小，是由于央行的监控和及时调节，为宏观逆周期调节的重要工具；工业增加值和出口所受冲击较大，折射出我国工业产出和出口在高状态下的高速增长和对整体经济状态的较强依赖性；利率所受到的冲击非常剧烈，这与利率变动较为灵活的特征密不可分；证券市场受到的冲击最大，说明股市对经济变动的反应最为敏感，但其中必然包含了超调的成分。

从本文的分析中我们可以得到这样的政策启示：政策当局在运用经济政策促进经济增长和稳定物价水平的同时，也应密切关注政策实施可能引起的股市波动，并根据经济所处的不同状态考虑股市所受的冲击及相应的调节方式。在扩张性政策时期，可以通过合理引导投资者的行为、增加非货币资产的短期投机成本，减小股票价格超调上涨带来的泡沫风险；在紧缩性政策时期，促进人民币升值会较扩张期对股市产生更强的带动作用。当经济处于过热状态时，积极治理通货膨胀有助于防止股市泡沫的膨胀；而当经济进入低迷状态时，提高市场流动性是提振股市较为有效的方式。另外，央行在选取利率作为政策工具时，应该明确政策信号，减少投资者预期的不确定性，避免引起股市的过度波动。