四旋翼无人机的反步RBF网络自适应控制

沈炜皓,李 众

(江苏科技大学电子信息学院,江苏镇江 212003)

四旋翼无人机作为新型的小型无人机,凭借其良好的机动性能,能够垂直起降,自由悬停。由于四旋翼具备这些优势,它被广泛应用于军事领域和民用领域,例如无人机群战场侦察[1]、快递投送、农业植保等[2]。就四旋翼的控制而言,其难点分为两个方面:第一,陀螺效应和外界干扰等因素的存在,使得建立准确的动力学模型异常困难;第二,四旋翼飞行器具有4个输入6个输出[3],其驱动、非线性、强耦合等特性[4]增加了设计高品质控制器的难度。针对四旋翼控制系统的设计,控制策略主要包括局部线性化、非线性控制和智能控制。局部线性化方法包括传统PID控制和最优LQR控制;非线性控制方法主要有反步法、滑模控制、预测控制、自适应控制、鲁棒控制等;智能控制方法有模糊控制、神经网络控制等。

针对四旋翼多变量、强耦合、复杂非线性的系统,反步法可以有效处理。但是,反步法对于模型中的不确定因素和外界干扰不具备良好的抵抗能力,所以通常将反步法和其他算法结合,提高其抗干扰性能。文献[5]运用自适应块反步控制法,设计了四旋翼飞行器姿态控制器。文献[6]设计了四旋翼无人机反步自适应控制器,在控制律中加入积分项,提高了系统的鲁棒性。文献[7]针对反步法的不足之处,提出一种将反步法与滑模自适应控制相结合的方法。文献[8]采用了积分饱和反步控制法,以此抵抗无人机所受的外界干扰。文献[9]利用滑模控制与RBF自适应相结合的方法,以此提高系统的抗干扰性。文献[10]为了提高四旋翼抗干扰性,将反步法与扩张状态观测器结合设计控制器。

本文从文献[7]、[9]中获得启发,在不考虑外界干扰时,利用反步法设计控制器;在考虑外界常值干扰和变值干扰时,在反步法的基础上,利用RBF网络逼近并补偿外界扰动,并通过Lyapunov方法设计RBF网络权值的自适应律,在线调整神经网络的权值。

1 四旋翼无人机的动力学模型

四旋翼无人机是欠驱动系统,因为它具有6个自由度,却仅含有4个控制输入。四旋翼的结构示意图如图1所示,其中地球坐标系为OE-XEYEZE,机体坐标系为OB-XBYBZB。调节4个电机的转速,无人机能够产生横滚、俯仰、偏航运动。相邻两对旋翼的旋转方向不同。保持旋翼1和旋翼3转速不变,增大旋翼2的转速,减小旋翼4的转速,将产生横滚运动;保持旋翼2和旋翼4转速不变,增大旋翼3的转速,减小旋翼1的转速,将产生俯仰运动;保持旋翼1和旋翼3转速不变,增大旋翼2和旋翼4的转速,将产生偏航运动。

图1 四旋翼结构示意图

建立较为准确、完整的描述系统运动的数学模型是设计控制器的前提条件。为了便于求解,给出下列假设:

1)四旋翼是刚体;

2)四旋翼的质量和转动惯量不变;

3)四旋翼的重心和几何中心一致[11]。

四旋翼无人机的位置由相对于地球坐标系下的坐标[xyz]T以及两个坐标系之间的夹角[ΦθΨ]T确定,其中[xyz]T表示无人机的位移,[ΦθΨ]T表示无人机产生的横滚角、俯仰角、偏航角。在机体坐标系下,利用Newton-Euler[12]法对四旋翼建模并简化,可得其动力学模型为

(1)

式中，m为机体质量,IX、IY、IZ为转动惯量,Ωr=Ω1-Ω2+Ω3-Ω4,Δi=f/m(i=1,2,3),f为风扰,m为四旋翼质量,l为旋翼中心至机体坐标系原点的距离,g为重力加速度,四旋翼的控制输入(U1,U2,U3,U4)与电机转速Ωi(i=1,2,3,4)之间的关系为

(2)

2 控制器设计

2.1 四旋翼状态方程

当不考虑x,y,z方向上的外界干扰时,可将四旋翼动力学方程式(1)表达为

(3)

其中,控制输入量为U=[U1U2U3U4]T,状态变量X为

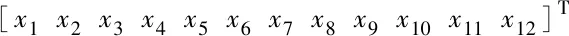
(4)

结合式(2)、(3)、(4)可得

(5)

表1 相关参数符号及含义

2.2 控制策略

本设计的控制策略为双环控制。外环为位置控制,由位置期望值xd、yd、zd与其实际值x、y、z作差,设计位置控制器U1、ux、uy。再进入内环姿态控制,由ux、uy反解算出期望姿态角Φd和θd,由期望姿态角Φd、θd、Ψd与实际值Φ、θ、Ψ作差,设计姿态控制器为U2、U3、U4。如此,整个控制流程如图2所示。

图2 控制流程框图

2.3 反步控制器设计

在无外界干扰的条件下,高度子系统的状态空间表达如下:

(6)

其中,

(7)

给定高度的期望值为zd=xd5,高度跟踪误差为

z1=xd5-x5

(8)

根据Lyapunov理论,假设高度子系统在点z1处达到平衡(z=zd),构造Lyapunov函数V(z1):

(9)

沿着系统的轨迹V(z1)的时间导数为

(10)

(11)

式(11)中,α1为可调控制器参数。

定义速度跟踪误差为

(12)

取Lyapunov函数为

(13)

沿系统的轨迹V(z1,z2)的时间导数为

(14)

所以,高度控制器U1设计为

-α2z2]m/(cosx7cosx9)

(15)

(16)

同理,可以设计其他通道控制器:

U2=[z3-a1x10x12+a2Ωrx10-α3(α3z3+z4)-α4z4]/b1

(17)

U3=[z5-a3x8x12+a4Ωrx8-α5(α5z5+z6)-α6z6]/b2

(18)

U4=[z7-a5x8x10-α7(α7z7+z8)-α8z8]/b3

(19)

水平位置控制器中采用两个虚拟控制量ux、uy:

ux=(cosφsinθcosψ+sinφsinψ)
uy=(cosφsinθsinψ-sinφcosψ)

(20)

由式(20)反解算出期望姿态角Φd和θd:

φd=arcsin(uxsinx11-uycosx11)

θd=arcsin[(ux-sinx9sinx11)/(cosx9cosx11)]

(21)

同理,运用反步法,控制律ux、uy可表示为:

(22)

2.4 反步RBF网络自适应控制器设计

当存在外部干扰时,传统反步法不能有效抵抗干扰,所以需要加入辅助控制来估计干扰并进行补偿。在传统反步控制的基础上,引入RBF自适应算法对干扰进行逼近,以此来增强控制系统的抗干扰性。当存在外界干扰时,可将非线性动力学方程(3)改写成

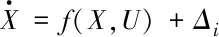
(23)

其中,Δi=f/m(i=1,2,3),f为x、y、z方向上的风扰,m为四旋翼质量。

存在外界干扰时,高度子系统的状态空间形式为

(24)

由前文反步法设计的高度控制器将表达为

α2z2+Δ3]m/(cosx7cosx9)

由于控制量U1中存在未知外界干扰Δ3,而传统反步法抗干扰能力较差,所以利用RBF网络的万能逼近特性,逼近外界干扰Δ3。RBF网络算法为

(25)

Δ3=f(x)=W*Th(x)+ε

(26)

其中,x是RBF网络输入,j是隐含层第j个节点,h=[hj]T是RBF网络的高斯基函数输出,W*是RBF的理想权值,ε是RBF网络的逼近误差[13]。

设计RBF网络权值自适应律为

(27)

其中,γ为设计参数,且γ>0。

取RBF网络输入为z2,z2为高度速度跟踪误差,则RBF网络输出为

(28)

定理考虑外界存在扰动的四旋翼无人机系统如式(23)所示,系统误差由式(31)控制,RBF网络权值的自适应律设计如式(27)所示,则四旋翼无人机系统将渐进稳定。

证明为证明反步RBF网络自适应控制的稳定性,构造Lyapunov函数为

(29)

则

(30)

设计高度控制律为

(31)

则

(32)

同理,可以设计其他通道的控制器。

3 仿真实验与分析

参考文献[12],选取四旋翼无人机的系统参数为m=0.5 kg,IX=0.006 kg·m2,IY=0.006 kg·m2,IY=0.012 kg·m2,b=3.13e-5 N·s2,d=7.5e-7 N·ms2,Jr=5e-5 kg·m2,l=0.3m,g=9.8 m/s2。

首先,在不考虑外界干扰的条件下,给定期望姿态角和期望位置,根据姿态控制效果和位置控制效果,验证本文反步控制器设计的正确性。其次,在考虑外界常值干扰和变值干扰的条件下,给定期望位置,进行定点控制实验。根据四旋翼无人机的位置误差,比较反步控制器和反步RBF网络自适应控制器的抗干扰性能。

1)当不考虑干扰时,验证传统反步法的姿态控制效果,如图3所示。姿态控制仿真初始条件是:姿态角为Φ=0.5 rad,θ=0.5 rad,Ψ=0.5 rad,仿真时间为6 s。控制目标:使四旋翼无人机达到期望姿态角Φd=0 rad,θd=0 rad,Ψd=0 rad。

2)当不考虑干扰时,验证传统反步法的位置控制效果,如图4所示。位置控制仿真初始条件是:x=2 m,y=2 m,z=5 m,姿态角均为零,仿真时间为6 s。控制目标:使四旋翼无人机到达期望位置xd=0 m,yd=0 m,zd=7 m。

图3 无干扰时反步法姿态控制

图4 无干扰时反步法位置控制

由图3和图4可知,当不考虑外界干扰时,利用反步法可以达到期望的姿态控制和位置控制效果,由于运用反步法设计的控制量中存在误差和误差的微分项,通过合理选取误差微分项系数,能够减小超调量。因此,在没有干扰的条件下,通过合理选取反步控制器的控制参数,可使得四旋翼无人机无超调且平滑地达到期望位置。由此可验证反步法设计的正确性。

3)从第0 s开始,在x、y、z方向上分别施加f=2 N的常值风扰时,反步法与反步RBF网络自适应法比较如下图5所示。仿真初始条件是:x=2 m,y=2 m,z=5 m,姿态角均为零,仿真时间为10 s。控制目标:使四旋翼无人机到达期望的位置xd=0 m,yd=0 m,zd=7 m。

图5 常值干扰下位置跟踪

4)从第0 s开始,在x、y、z方向上分别施加f=0.5sin(t)N的变值风扰时,反步法与反步RBF网络自适应法比较如图6所示。仿真初始条件:x=2 m,y=2 m,z=5 m,姿态角均为零,仿真时间为10 s。控制目标:使四旋翼无人机到达期望位置xd=0 m,yd=0 m,zd=7 m。

从图5可以看出,反步法是一种递归设计方法,将高阶系统分解成低阶子系统,设计Lyapunov函数并构造中间虚拟控制量保证子系统镇定,通过合理选取参数,可以使得调节过程平滑无波动。但是,当在x、y、z方向上施加常值干扰时,利用反步法反步法无法有效抵抗干扰,不能将实际位置调节至期望位置,存在较大的稳态误差,而采用本文设计的方法,RBF网络能对外界常值干扰进行有效估计和补偿,在3 s左右使得实际位置到达期望位置,且稳态误差较小。从图6中可以看出,当在x、y、z方向上施加变值干扰时,相比于反步法,由于RBF网络对时变干扰具有一定的补偿和抑制作用,反步RBF网络自适应法的调节时间更短,随干扰变化幅度更小。所以本文设计的方法比传统反步法抗干扰性能好。

图6 变值干扰下位置跟踪

4 结束语

1)将RBF网络引入传统反步法中,并设计神经网络权值自适应律,设计出了基于反步法的RBF网络自适应控制器,可用于四旋翼无人机飞行控制。

2)根据Lyapunov稳定性定理,证明运用反步RBF网络自适应方法控制的四旋翼无人机系统是渐进稳定的。

3)定点控制仿真实验表明,传统反步法抵抗常值干扰和变值干扰的能力较差。相反,本文设计的控制算法抗干扰性更好。