基于分布式信息融合的多传感器目标定位算法

陈林秀,宋 闯,范 宇,张 航

(复杂系统控制与智能协同技术重点实验室,北京 100074)

随着现代高科技与电子设备的飞速发展,战场电磁环境日益复杂,舰艇平台防御体系日趋完善,使得依靠单一模式制导的反舰武器已经难以完成对目标的稳定跟踪与精确打击要求[1]。主/被动雷达双模复合制导作为多模复合制导中的一种典型制导模式,受到了极大的关注。主动雷达量测精度高,既有距离信息,又有角度、多普勒信息,但由于它主动发射电磁波,易被敌方的探测器截获,相对来说易受敌方干扰和攻击。被动雷达本身不发射电磁波,具有隐蔽性好、作用距离远、提取目标属性信息多等优点,具有复杂战场环境电磁感知与侦察优势,但被动雷达存在着测角精度差、无法测距等问题[2-4]。将二者进行结合,能够实现性能互补,大大提高武器系统的作战效能与生存能力。但如何有效地融合主/被动雷达的信息是一个难点问题。

信息融合算法设计是主/被动雷达复合制导技术的核心,其本质属于多传感器信息融合范畴。按照信息抽象的5个层次,信息融合可分为检测级融合、位置级融合、属性(目标识别)级融合、态势评估和威胁估计[5]。本文研究采用的主被动雷达信息融合跟踪算法属于位置级融合。从多传感器系统的信息流通形式和综合处理层次看,典型的位置级数据融合方式主要分为集中式融合、分布式融合和混合式融合 3 种[6]。集中式融合估计是将所有传感器信息集中到一个观测方程,即对观测状态进行扩维,最后输出融合状态估计,这种方式信息损失小,但计算量大,当存在传感器异常时可能导致滤波器发散[7]。分布式融合方式是先将各传感器测量的信息进行预处理,滤去一些不相干的杂波以及干扰之后，再送入融合中心进行融合,这类融合方式计算量小,而且不受单一传感器异常影响[8-9]。由于主动雷达在跟踪末段容易受到目标采用电磁波干扰、欺骗、伪装和隐蔽等手段的干扰,本文采用分布式融合结构,首先利用非线性滤波技术对主/被动雷达量测信息进行处理,形成主/被动雷达目标跟踪航迹,然后进行航迹的融合。

1 主/被动雷达信息融合方案

对于主/被动雷达复合导引头系统来讲,主动雷达可以对目标方位角、高低角及距离进行测量;被动雷达可以观测目标的方位角和高低角。对于分布式信息融合结构来说,融合一般包括时空对准、单传感器航迹形成、数据对齐、数据关联以及航迹融合等内容。本文以文献[10]中的主/被动雷达复合导引头模型为参考,即主/被动雷达天线采用共口径设计,其观测角度相同;并且主/被动雷达通过时钟同步工作,量测信息为同一时刻的目标信息;于是,对于主/被动雷达复合制导的飞行器跟踪单目标的信息融合问题,融合的总体结构设计如图1所示。

图1 主/被动雷达信息融合总体结构

在主/被动雷达都达到对目标进行正常观测条件后,首先利用非线性滤波技术对主/被动雷达量测信息进行处理,分别形成主/被动雷达独立的目标跟踪航迹,将获得的两条航迹送入融合中心进行目标状态的融合,为进一步充分利用目标的先验信息与观测信息,将融合中心输出的目标估计状态和估计协方差反馈至主/被动雷达独自跟踪的滤波器,以提高融合系统的目标定位精度。若主动雷达在目标跟踪过程中被干扰时,利用先验信息对目标状态进行外推,形成虚拟的主动雷达跟踪航迹,最后与被动雷达跟踪航迹在融合中心进行状态的融合。

2 主/被动雷达信息融合关键技术

2.1 非线性滤波器技术

本文采用无迹卡尔曼滤波(UKF)、三阶容积卡尔曼滤波(CKF)、五阶容积卡尔曼滤波(FCKF)、中心差分卡尔曼滤波(CDKF)以及粒子滤波(PF)算法来形成主/被动雷达独自的目标跟踪航迹。前四种属于卡尔曼系列算法,是依据不同的方法及准则来处理非线性,再根据标准卡尔曼滤波思想进行融合,最后一种即粒子滤波(PF)的核心是蒙特卡洛采样的思想[11-12]。这些算法都是在目标的状态模型和观测模型基础上进行的。

1)系统状态模型

在地心笛卡尔坐标系下,目标的状态方程为

Xk+1=Fk+1/k·Xk+Gk+1/k·Vk

(1)

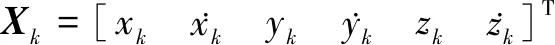
状态转移矩阵Fk为

其中,T为仿真步长。

过程噪声驱动矩阵Gk为

2)观测模型

主动雷达观测模型为

(2)

被动雷达观测模型为

(3)

2.2 带反馈的协方差交叉融合算法

交叉可以用协方差的凸组合来描述,协方差交叉算法如下

(4)

3 仿真分析

3.1 仿真条件

假设飞行器和目标均进行匀速直线运动。目标在地心直角坐标系下的初始状态为:Xecef,0=[-1 055 593 m -3.5 m/s 4 711 338 m -80 m/s 4 153 729 m 89 m/s]T;目标在飞行器地理坐标系下的初始状态为:Xenu,0=[1 750 m 21m/s 17 973 m -382 m/s -9 272 m 140 m/s]T，Xecef,0和Xenu,0分别表示目标在对应坐标系下x,y,z三个方向上的位置和速度。

本次仿真的时间为85 s;仿真步长为0.01 s,主动雷达量测噪声为:均值为0,方差为(100 m2,0.4度2,0.4度2)的白噪声。被动雷达量测噪声为:均值为0,方差为(1.0度2,1.0度2)的白噪声。

本次仿真使用位置的均方根误差(RMSE)作为性能指标。k时刻目标位置的RMSE为

(5)

3.2 非线性滤波算法仿真

3.2.1 主动雷达目标跟踪状态单独滤波估计仿真

如图2、3所示,当观测信息为角度和距离时,粒子滤波的收敛性最佳,五阶容积卡尔曼滤波具有相对较好的滤波稳定性和估计精度。中心差分卡尔曼滤波在仿真运行后期也表现出了较好的滤波精度,但是其前期的滤波性能较差。除粒子滤波外,其他滤波器随着仿真时间增长,它们滤波精度的差别越来越小。综上,在后面进行主/被动雷达数据融合时,将采用五阶容积卡尔曼滤波对主动雷达的观测信息进行单独滤波处理。

图2 目标位置的均方根误差(主动雷达)

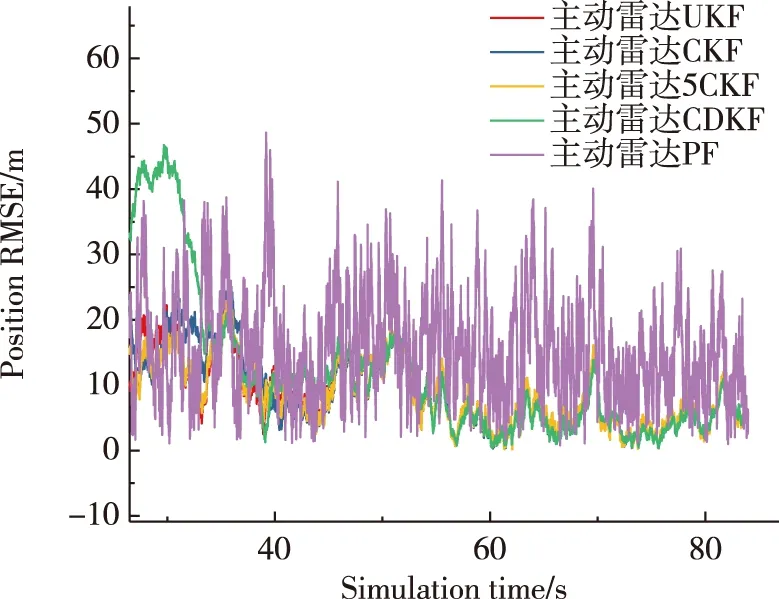
图3 目标位置的均方根误差(图2部分放大图)

3.2.2 被动雷达目标跟踪状态单独滤波估计仿真

如图4、5所示,当观测信息仅有角度时,与主动雷达量测信息单独滤波结果相比,该条件下各种滤波器的收敛时间均增长,滤波误差增大。其中,粒子滤波仍然具有较好的收敛性能,容积卡尔曼滤波在滤波后段的滤波精度明显优于其他滤波器。因此,在后面进行主/被动雷达数据融合时,将采用容积卡尔曼滤波对被动雷达的观测信息进行单独滤波处理。

图4 目标位置的均方根误差(被动雷达)

图5 目标位置的均方根误差(图4部分放大图)

3.3 数据融合仿真

3.3.1 主被动雷达均正常工作条件下的融合仿真

由图6、7可知,采用协方差交叉融合算法可以得到比单传感器独自滤波更精确的状态估计。

图6 目标位置的均方根误差(主被动正常融合)

图7 目标位置的均方根误差(图6部分放大图)

3.3.2 主动雷达被干扰条件下的状态融合仿真

假设当仿真时间T>a秒时,经检测分析后,确定主动雷达被干扰,主动雷达失效,此时将根据第一节所述的融合方案进行主/被动雷达目标状态的融合。

1) 主动雷达在其独自滤波跟踪收敛后(T≥25 s)被干扰

①T>70 s,主动雷达被干扰(如图8、9);

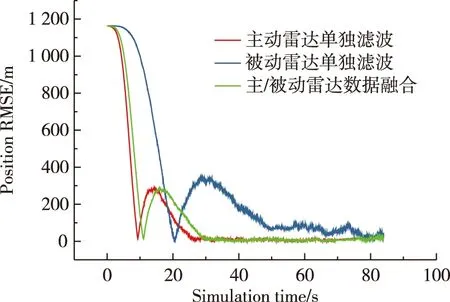
图8 目标位置的均方根误差(T>70 s主动雷达失效)

图9 目标位置的均方根误差(图8部分放大图)

②T>50 s,主动雷达被干扰(如图10、11);

图10 目标位置的均方根误差(T>50 s主动雷达失效)

图11 目标位置的均方根误差(图10部分放大图)

③T>25 s,主动雷达被干扰(图12);

图12 目标位置的均方根误差(T>25 s主动雷达失效)

2) 主动雷达在其独自滤波跟踪未收敛时(T<25 s)被干扰

当T>15 s,主动雷达被干扰，如图13所示。

图13 目标位置的均方根误差(T>15 s主动雷达失效)

仿真结果表明,若主动雷达在其独自滤波跟踪收敛后被有源干扰,利用信息融合方法可以得到优于被动雷达单独滤波的目标定位精度,若主动雷达在独立滤波未收敛时被干扰,由于先验的主动雷达观测信息得到的状态估计存在较大的误差,此时将其送入融合中心再进行信息融合,会带入这部分误差,对融合结果不利。

4 结束语

本文针对多传感器信息融合中的主被动雷达数据融合问题,制定了主/被动雷达复合导引头信息融合的总体方案,在分布式信息融合结构下,通过仿真,分析比较了主动雷达和被动雷达单独滤波条件下五种非线性滤波算法的估计性能;在信息融合中心采用带反馈的协方差交叉融合算法,充分利用了主/被动雷达的观测信息,具有较好的融合效果。特别针对主动雷达容易受干扰的特点,仿真分析了在不同干扰条件下融合算法的性能;结果表明,若主动雷达在其独自跟踪滤波收敛后被有源干扰,基于信息融合方法得到目标状态估计更稳定,且估计精度更高。