一种GA-BP神经网络模型的RSSI测距算法

余振宝，卢小平，陶晓晓，周雨石，皇永波

一种GA-BP神经网络模型的RSSI测距算法

余振宝，卢小平，陶晓晓，周雨石，皇永波

（河南理工大学 矿山空间信息技术国家测绘地理信息局重点实验室，河南 焦作 454000）

路径损耗模型；遗传算法；反向传播神经网络；测距精度；室内定位

0 引言

基于位置的服务（location based service, LBS）主要分为室外定位和室内定位2个部分。在室外环境中，全球卫星导航系统（global navigation satellite system, GNSS）可以提供准确的位置服务[1-2]。但是由于室内环境相对较为复杂多变，仅依靠全球卫星导航系统不能实现准确的室内定位，因此大量学者研究基于无线传感器网络（wireless sensor network ,WSN）的室内定位技术[3]。

WSN室内定位技术主要分为基于测距（range-based）和基于非测距（range-free）的定位算法[4]。基于测距的定位算法主要有：到达时间（time of arrival, TOA）[5]、到达时间差（time difference of arrival, TDOA）[6]、到达角度（arrange of arrival, AOA）[7]、基于接收信号轻度（received signal strength indication, RSSI）[8]等方法。基于非测距的定位算法主要有：质心算法、DV-Hop算法、APIT算法、指纹数据库定位算法[9-10]。基于非测距定位算法在精度上要比基于测距定位算法的精度高，因此基于RSSI的室内定位算法成为目前研究重点，但因信号强度在室内环境中传播易受环境影响，因此建立准确的无线信号路径损耗模型是研究的重点。文献[11]中对采集到的数据进行高斯滤波处理，然后利用处理后的信号强度估算距离值。文献[12]分析了灰度理论和径向基函数（radical basis function, RBF）神经网络，并对 2者进行结合构建无线信号路径损耗模型，通过实验证明该方法提高了测距精度。文献[13]针对反向传播（back propagation, BP）神经网络存在收敛速度较慢的问题，提出了莱文贝格-马夸特（Levenberg-Marquardt，LMBP）算法，通过MATLAB模拟仿真显示，该算法提高了收敛速度，同时提高了定位精度。文献[14]在分析传统路径损耗模型的基础上提出了利用BP神经网络训练无线信号路径损耗模型，最后通过模拟仿真证明BP神经网络模型比传统的信号路径损耗模型测距精度要高。本文在研究BP神经网络的基础上提出了遗传算法（genetic algorithm, GA）优化BP神经网络的路径损耗模型，该方法利用遗传算法寻找最优的初始权值和阈值，然后将其赋值于BP神经网络，从而提高测距精度，为基于RSSI测距的室内定位算法提供重要依据。

1 传统路径损耗模型及其分析

1.1 自由空间传播模型

自由空间模型是指信号传播的过程中没有任何阻碍，不发生散射、反射、衍射的理想状态下，接收到的信号强度与信号传播距离之间的关系，可以用Friis公式[15]表示为

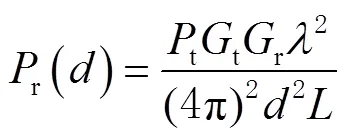
在实际的环境中不可能是理想的状态，有学者在自由空间模型的基础上通过大量的实验得出对数-常态模型[16]（lognormal model）为

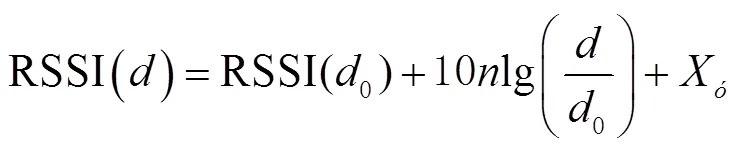
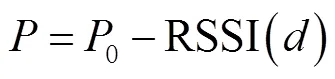
由式（2）及式（3）可以得出常用的无线信号路径损耗模型公式为

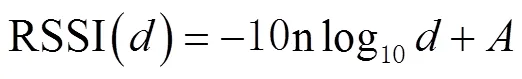
式中为1 m处的信号强度。

1.2 分析环境参数A和n

在传统的无线信号路径损耗模型中，估算的距离值受环境参数和（为路径损耗因子）的影响较大。对不同参数进行模拟仿真，选取走廊作为模拟环境，取=-28 dB·m，值分别取1.8、2.0、2.2、2.4、2.4、2.6、2.8，将其分别代入式（4）中得到不同的拟合曲线，如图1所示。

图1 A值固定不同n值对应的衰减模型曲线

由图1可以看出，在环境参数确定的情况下，参数直接影响信号的衰减速率，值与衰减速率成正相关，即随着值的增大，信号衰减速率也增大，无线信号传播的有效距离在缩短。同时也可以得出：参数值取值稍有偏差直接影响估算的距离值。

验证参数对估算距离的影响，假设参数不变，选取=2.0，值分别为-27、-28、-29、-30、-31、-32 dB·m然后分别代入式（4）中得到不同的拟合曲线，如图2所示。

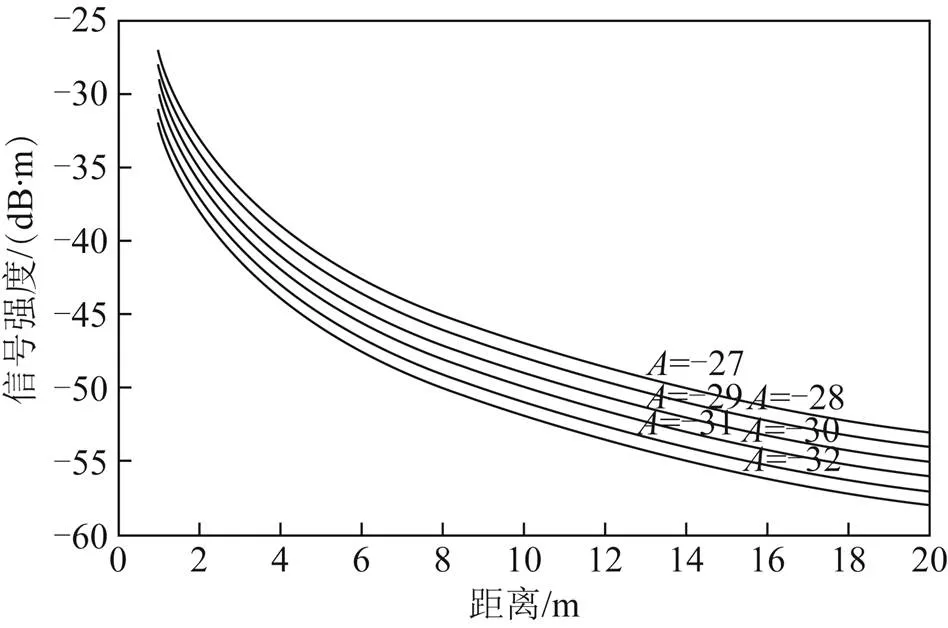
图2 n值固定不同A值对应的衰减模型曲线

从图2中可以看出，当值固定的情况下，参数对信号衰减速率没有影响，随着值的增大，信号传播的有效距离也在不断增大。参数选取不当会直接影响估算距离值的整体偏移。

2 基于GA-BP神经网络训练路径损耗模型

由上述分析可知传统的路径损耗模型估算的距离值受环境参数、的影响较大，环境参数、的选取不当直接影响距离值的估算，从而直接影响基于测距的室内定位算法的精度。由Kolmogorov定理可知，任意1个非线性的连续函数都可以由3个3层的BP神经网络来实现，同时由图2、图3可以得出无线信号衰减与距离值之间是非线性的，因此由神经网络来拟合信号传播距离与信号强度之间的关系可以很好地避免对环境参数的依赖。

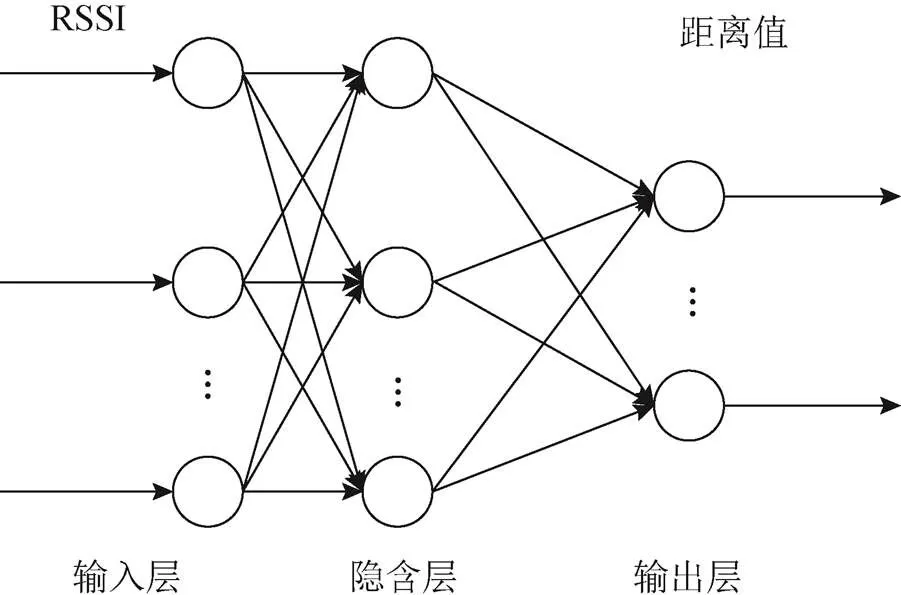
图3 BP神经网络结构

2.1 BP神经网络

BP神经网络是1种误差逆向传播的前馈神经网络，主要由输入层、隐含层、输出层3部分组成（如图（3）所示），其中每层之间的神经元相互独立，但前1神经元与后1神经元相互关联。BP神经网络主要包括正向传播和反向传播2个过程。

正向传播：正向传播指的是从输入层开始，输入值乘以对应的权值，然后再加上其对应的偏置，最后通过激励函数得到输出值，计算公式为

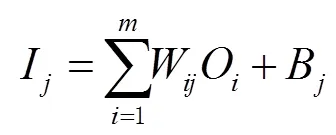
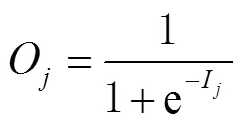
反向传播：通过正向传播可以计算出输出值，输出值与真实值之间会存在1个误差，误差函数可以表示为

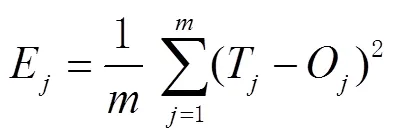
通过式（7）计算出最后1层误差，然后将该误差利用梯度下降法进行反向传播，经过隐含层直到最上1层，从而对权值和阈值进行更新，然后再进行正向传播过程计算输出值，直到输出值与真实值之间的差值小于设置的范围为止，否则继续更新权值和阈值。计算公式为

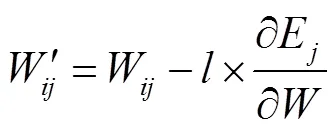
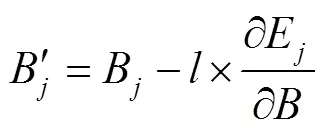
2.2 GA-BP神经网络训练路径损耗模型

BP神经网络算法是根据梯度下降法进行计算，当遇到复杂的非线性函数问题时，该算法会出现局部极小解，而不是全局最小解。因此在BP神经网络的基础上引入遗传算法，该算法是模拟生物界适者生存、优胜劣汰的生存法则。通过杂交、变异等操作进行繁衍使优良基因得以传递给后代。利用遗传算法寻找阈值和权值的最优值，然后再将其赋值给BP神经网络，将接收到的信号强度作为输入值，距离值作为输出值进行训练，算法流程如图4所示。

1）处理数据：在实验场地不同的位置利用移动设备进行信号采集，记录距离值与其对应的信号强度值，对测得的信号强度进行高斯滤波处理，然后再将信号强度作为输入值，距离值作为输出值。

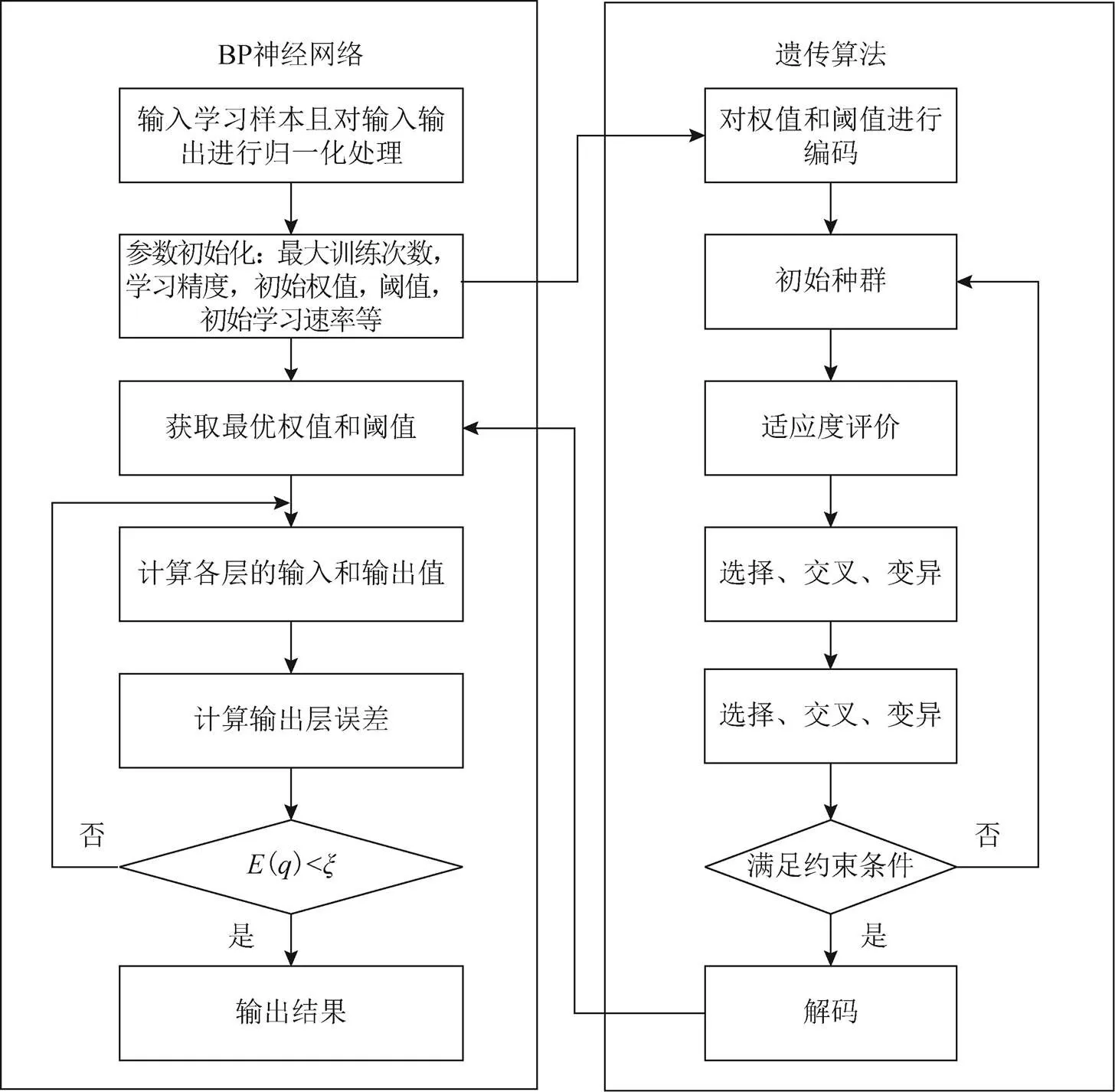
图4 GA-BP神经网络流程

算法的具体步骤为：

2）对初始总群进行编码：采用实数编码的方法对初始总群进行编码。假设输入层节点数为，输出层节点数为，隐含层节点数为，则编码长度为

3）适应度值计算：适应度函数的选择直接影响到最终的结果，个体根据适应度值进行选择，将适应度高的个体留下，将BP神经网络中的误差函数的倒数作为适应度函数，即

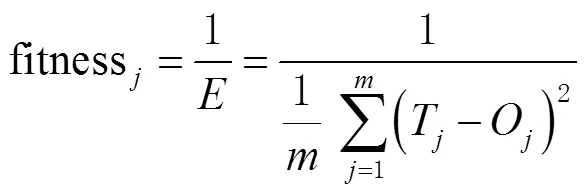
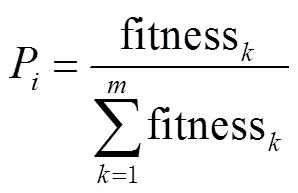
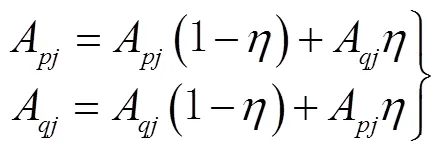
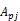
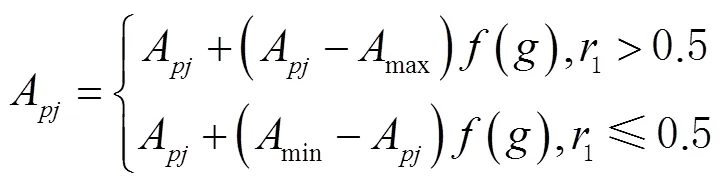
7）重复上述操作，直到达到预设的条件终止训练，否则继续训练。

8）将选择出的目标个体进行解码，并将权值和阈值赋值于BP神经网络。

9）利用最优的权值和阈值对网络进行训练，直到输出值与真实值之间的差值小于预设值或者达到最大训练次数结束训练。

3 实验与结果分析

3.1 模拟仿真实验

为了验证GA-BP神经网络训练的无线信号路径损耗模型的测距精度，采用MATLAB2014a进行模拟仿真实验。考虑到有无线保真（wireless fidelity,WiFi）信号的有效传播距离为20 m，因此在1~20 m之间随机生成30个数作为距离值，然后取环境参数=-28 dB·m、=1.8作为环境参考值，利用式（4）的无线信号路径损耗模型计算距离值对应的信号强度值，然后对生成的信号强度中加入均值为0、方差为1高斯白噪声，以模拟数据的真实性。随机取21对距离值及其对应的信号强度值作为GA-BP神经网络和BP神经网络训练数据，剩下的9个信号强度值作为GA-BP神经网络和BP神经网络的输入值，其对应的距离值作为真值，然后利用经GA-BP神经网络和BP神经网络预测出的距离值与真值的差的绝对值（Δ1、Δ2）作为评价标准，Δ1、Δ2的计算方法为

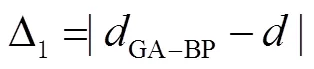
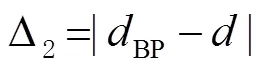
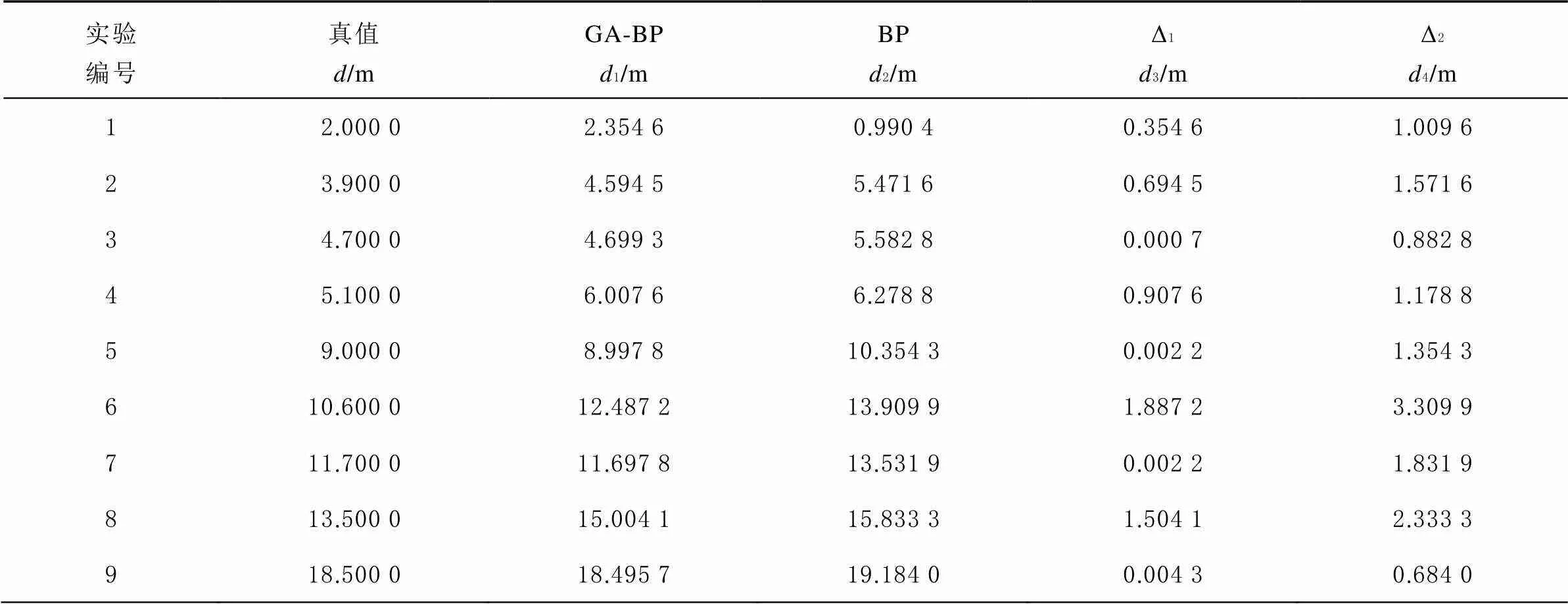
表1 模拟数据测距对比

注：为真实的距离值；1为GA-BP估算的距离值；2为BP估算的距离值；3为GA-BP预测距离的误差值；4为BP预测距离的误差值。

由表1可得：GA-BP神经网络构建的无线信号路径损耗模型估算的距离值的最大误差为1.887 2 m，最小误差为0.000 7 m，平均误差为0.595 3 m。BP神经网络构建的无线信号路径损耗模型估算的距离值最大误差为3.3099 m，最小误差为0.684 0 m，平均误差为1.5729 m。上述2种算法计算得出的最大误差：1.8872 m <3.3099 m、最小误差0.0007 m< 0.6840m、平均误差0.5953 m<1.5729 m。由此可得无论是最大测距误差、最小测距误差还是平均测距误差，本文提出的GA-BP神经网络的信号损耗模型都要比BP神经网络的信号损耗模型要小。

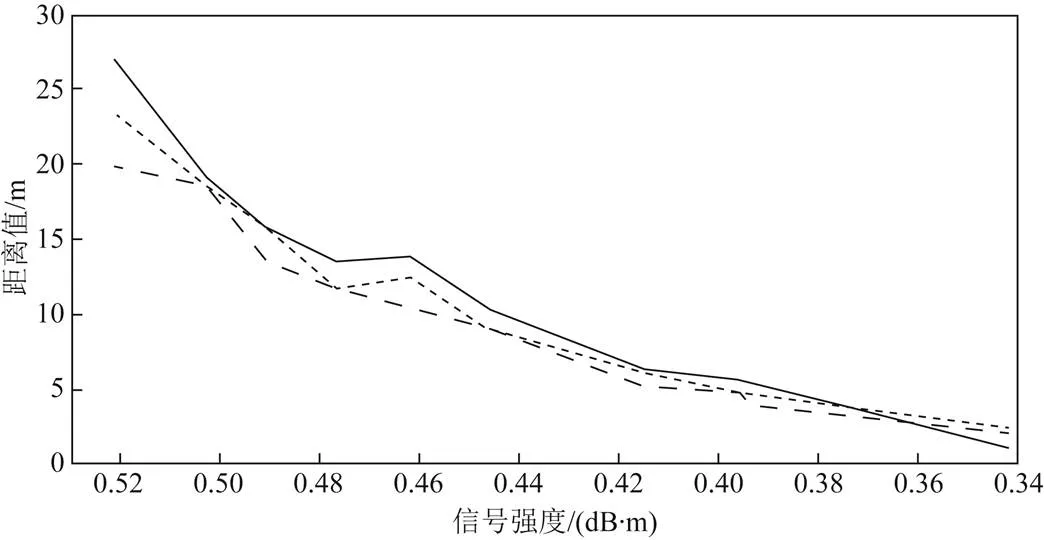
图5 距离对比

图5表示真实的距离值、GA-BP神经网络构建的无线信号路径损耗模型估算的距离值和BP神经网络构建的无线信号路径损耗模型估算的距离值。由图5可以看出：GA-BP神经网络构建的无线信号路径损耗模型估算的距离值比BP神经网络构建的无线信号路径损耗模型估算的距离值更加接近于真实的距离值。

3.2 实测实验

选取空旷的阳台作为实验场地，利用手机作为移动端放在22个不同的位置上进行信号采集，每个不同的位置采集100次信号强度，利用2倍中误差进行粗差的剔除，然后再求其平均值作为该点的信号强度值（如表2所示）。

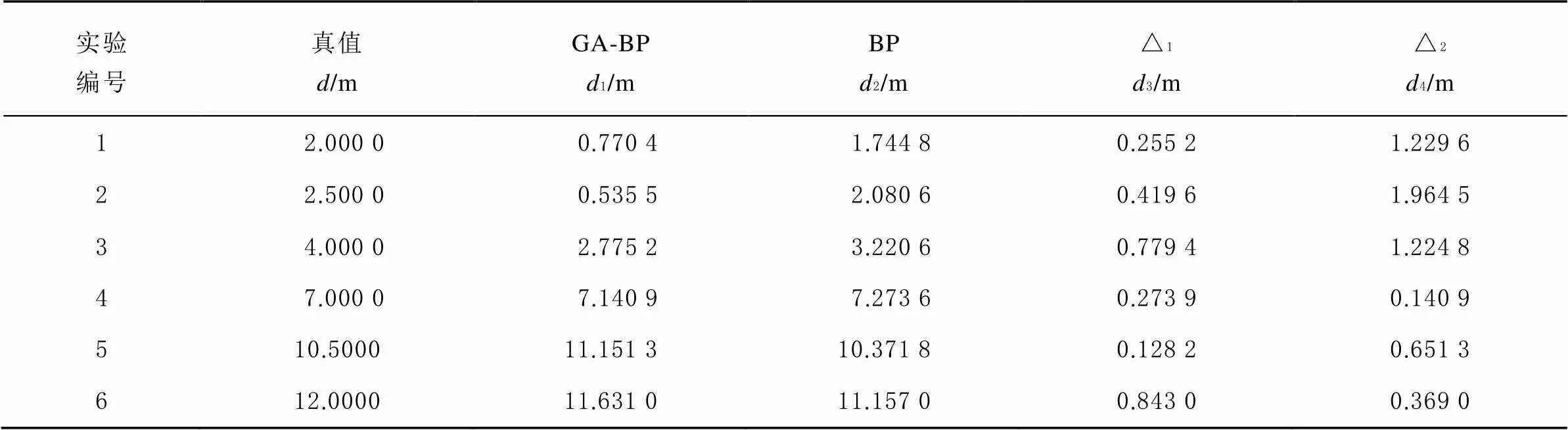
表2 实测数据测距对比

由表2可以看出GA-BP神经网络构建的无线信号路径损耗模型估算的距离值的最大误差为0.8430 m，最小误差为0.2552m，平均误差为0.4498 m。BP神经网络构建的无线信号路径损耗模型估算的距离值最大误差为1.9645m，最小误差为0.140 9m，平均误差为0.9300 m。上述2种算法计算得出的最大误差0.8430 m <1.9645 m、最小误差0.2552 m>0.1409m、平均误差0.4498 m< 0.9300 m。虽然在最小误差上本文提出的方法比BP神经网络预测的距离值误差大，但是最大误差和最小误差都有所减小，因此通过上述实测数据可以得出本文的GA-BP神经网络构建的无线信号损耗模型的测距精度比BP神经网络构建的无线信号路径损耗模型的测距精度平均提高了0.4498 m。

由文献[14]可以得知BP神经网络构建的无线信号路径损耗模型比传统的无线信号路径损耗模型预测的距离值的精度要高，同时由上述模拟数据和实测数据可以得出：本文提出的无线信号路径损耗模型的测距精度比BP神经网络构建的无线信号路径损耗模型以及传统的无线信号路径损耗模型的测距精度都要高。

4 结束语

本文通过对传统无线信号路径损耗模型分析，发现其预测的距离值受环境参数和的影响较大，因此利用神经网络构建无线信号路径损耗模型，在对BP神经网络构建的无线信号损耗模型的基础上进行了改进，提出了利用GA-BP神经网络构建无线信号损耗模型。该模型利用遗传算法对BP神经网络进行优化，提高测距精度。通过实测验证得出：本文提出的GA-BP神经网络构建的无线信号路径损耗模型比文献[14]提出的BP神经网络构建的无线信号路径损耗模型测距精度平均提高了48 %。本文提出的测距算法可为基于测距的室内定位算法提供参考。

[1]李维, 黄鹤, 罗德安. 改进粒子滤波器的室内地磁匹配精度研究[J]. 测绘科学, 2018, 43(7): 109-114, 120.

[2]宋斌斌, 余敏, 何肖娜, 等. 一种BP神经网络的室内定位WiFi标定方法[J]. 导航定位学报, 2019, 7(1): 43-47.

[3]李英玉, 陈刚. 基于人工神经网络的RSSI测距的牛顿定位算法[J]. 仪表技术与传感器, 2017(8): 122-126.

[4]龙佳, 卑璐璐, 张申, 等. 基于虚拟信标节点的改进加权质心定位修正算法[J]. 微电子学与计算机, 2017, 34(3): 74-78.

[5]邹延宾. TOA/TDOA定位的凸优化方法研究[D]. 成都: 电子科技大学, 2018.

[6]SEO H, KIM H, KANG J, et al. 3D moving target tracking with measurement fusion of TDoA/FDoA/AoA[J]. ICT Express, 2019, 5(2): 115-119.

[7]TOMIC S, BEKO M, DINIS R, et al. Bayesian methodology for target tracking using combined RSS and AoA measurements[J]. Physical Communication, 2017(25): 158-166.

[8]KARTHICK N, PRASHANTH K, VENKATRAMAN K, et al. Location estimation using RSSI and application of extended Kalman filter in wireless sensor networks[EB/OL].[2019-06-18].https://wenku.baidu.com/view/ ff50697c27284b73f242507f.html.

[9]KAUR A, KUMAR P, GUPTA G P. et al. A weighted centroid localization algorithm for randomly deployed wireless sensor networks[J]. Journal of King Saud University-Computer and Information Sciences, 2019, 31(1): 82-91.

[10]陶育仁. 基于WLAN位置指纹的室内定位技术研究[D]. 南京: 南京邮电大学, 2017.

[11]LUO X, BRIEN W J, JULIEN C L. Comparative evaluation of received signal-strength index based indoor localization techniques for construction job sites[J]. Adv. Eng. Informat, 2011, 25(2): 355-363.

[12]李丽娜, 梁德骕, 马俊, 等. 基于灰色-RBF神经网络的传播损耗模型训练[J]. 计算机应用与软件, 2016, 33(8):136-140.

[13]邹自明, 何文斌, 杨小平. 基于LMBP神经网络的无线室内定位方法[J]. 桂林理工大学学报, 2018, 38(3): 574-578.

[14]费扬, 杜庆治. 基于BP神经网络模型的RSSI测距方法研究[J]. 电波科学学报, 2018, 33(2): 195-201.

[15]李桢, 黄劲松. 基于RSSI抗差滤波的WiFi定位[J]. 武汉大学学报(信息科学版), 2016, 41(3): 361-366.

RSSI ranging algorithm based on GA-BP neural network model

YU Zhenbao, LU Xiaoping, TAO Xiaoxiao, ZHOU Yushi, HUANG Yongbo

（Key Laboratory of Mine Spatial Information and Technology of NASMG, Henan Polytechnic University, Jiaozuo, Henan 454000, China）

Aiming at the problem that it is liable to environmental parametersand(represents the signal strength at 1 m andrepresents the path loss factor) for the traditional wireless signal path loss model in the prediction of distance values, a wireless signal path loss model based on BP neural network optimized by genetic algorithm (GA) was proposed: the path loss model of wireless signal based on BP neural network was analyzed; and genetic algorithm was used to optimize the initial weights and thresholds of BP neural network, which helps overcome the defect of local minimum solution of BP neural network. Experimental result showed that the ranging accuracy of the proposed model could be average 48 % higher than that of the wireless signal path loss model with BP neural network, meanwhile avoiding the dependence on environmental parameters.

path loss model; genetic algorithm (GA); back propagation (BP) neural network; ranging accuracy; indoor location

P228

A

2095-4999(2020)02-0063-06

余振宝，卢小平，陶晓晓，等. 一种GA-BP神经网络模型的RSSI测距算法[J]. 导航定位学报,2020,8(2): 63-68.（YU Zhenbao, LU Xiaoping, TAO Xiaoxiao, et al. RSSI ranging algorithm based on GA-BP neural network model[J]. Journal of Navigation and Positioning, 2020, 8(2): 63-68.）

10.16547/j.cnki.10-1096.20200211.

2019-07-12

国家重点研发计划项目（2016YFC0803103）；河南省高校创新团队支持计划项目（14IRTSTHN026）。

余振宝（1993—），男，河南新乡人，硕士研究生，研究方向为室内外一体化定位。

卢小平（1962—），男，河南焦作人，博士，教授，研究方向为室内外一体化定位。