联合历元间差分相位和GRAPHIC组合的定位方法

杨武召，阮仁桂，孙中苗，刘 宁，李 鼎

联合历元间差分相位和GRAPHIC组合的定位方法

杨武召1，阮仁桂2，孙中苗2,3，刘 宁1，李 鼎1

（1. 长安大学 地质工程与测绘学院，西安 710054；2. 西安测绘研究所，西安 710054；3. 地理信息工程国家重点实验室，西安 710054）

为了进一步研究通用航空及无人机产业中低成本、小型化及实时性导航的解决方案，提出1种基于历元间差分相位和非差半合组合观测量（GRAPHIC）的单频单点定位方法，该方法不需要外部的星历、钟差或电离层改正信息，可用于实时导航。采用国际全球卫星导航定位系统服务组织（IGS）观测站数据对该方法进行验证，结果表明：滤波收敛之后，单频定位结果在、及方向的精度(RMS)分别达到0.54、0.35及0.71 m，3维位置精度达到0.96 m，与传统的单频伪距单点定位结果相比，分别提高了6.14 %，56.43 %，73.3 %，也显著优于双频伪距单点定位的精度。

单频；历元差分；单点定位；非差半合组合观测量（GRAPHIC）；精度

0 引言

全球卫星导航系统（global navigation satellite system, GNSS）具有全球性、全天候的实时连续授时和3维定位的能力，在交通运输、工程测量、形变监测、农业生产、通信等诸多领域得到广泛应用[1]。GNSS通常可提供单频或双频定位服务，后者的优势是可以利用双频组合消除电离层影响从而获得更高的定位精度，前者的优势是用户接收机成本更低。事实上，单频用户占据了GNSS用户的绝大部分。因此，提高GNSS单频用户的定位精度始终是研究的热点。广域增强系统就是成功的案例，如美国的广域增强系统（wide area augmentation system, WAAS）和欧洲静地轨道卫星导航重叠服务（European geostationary navigation overlay service, EGNOS），它们主要目的就是用于提供航空用户（仅使用L1频点）的定位精度和完好性。此外，近年来还发展了通过提供精密轨道、钟差和电离层改正数产品的单频精密单点定位技术[2]。这2种技术都要求用户接收机能够接收导航电文之外的增强信息，而这些信息通常需要专门的服务系统（包括监测站网络、运算中心和通信链路等）提供，这无疑大幅度提高了用户使用成本，致使其应用领域大大受限。

本文针对单频接收机的实时定位应用，提出了1种基于历元间差分载波相位和非差半合组合观测量（group and phase ionospheric correction, GRAPHIC）的实时单频精密单点定位方法，并开发相应的定位软件。

1 数学原理

1.1 单频GPS观测量

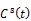
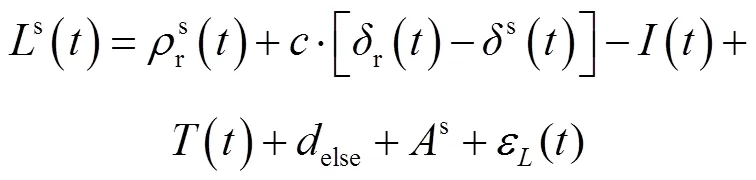
1.2 历元间差分模型

载波相位的精度可以达到毫米量级，远远高于伪距测量精度。为了获得高精度的定位结果，需要充分利用载波相位观测量。在精密单点定位应用中，通常采用非差观测量以实现精密的位置和钟差解算，如果对钟差不关注，也可以等价地采用星间单差观测数据。无论是非差还是单差观测数据都需要同时解算对应每个跟踪卫星的模糊度参数。在对计算效率要求较高的实时定位中，可以通过对相邻历元的载波相位观测量求差来消除相位模糊度参数，从而显著减少未知参数个数，降低对计算机资源的要求[3]。

对于连续跟踪的卫星，相邻历元间的载波相位差分观测量可表示为

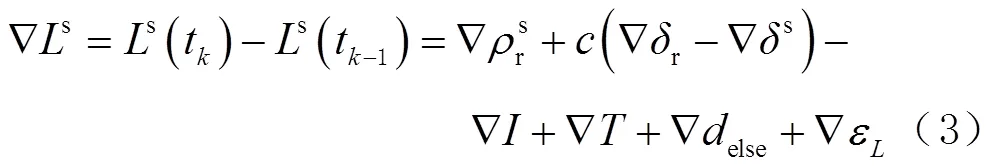
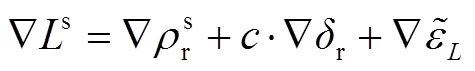
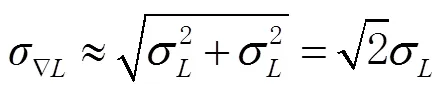
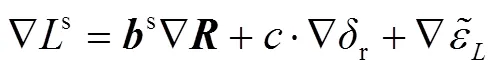
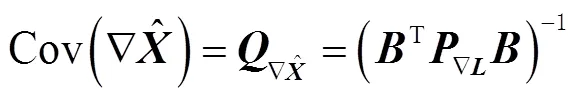
1.3 GRAPHIC组合

与双频观测数据相比，单频数据处理的难处在于电离层误差的处理。常用的方法是用电离层模型进行改正，如高精度的事后全球电离层格网模型对电离层延迟改正效果可以达到90 %以上[7]。另1种方法是利用电离层延迟对码伪距和载波相位的影响量级相等且符号相反的性质，构造单频无电离层线性组合观测量即GRAPHIC组合，这1组合是由文献[8-10]于1993年提出的，可以表示为

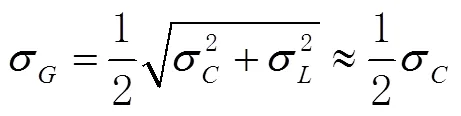
由式（10）可以看出GRAPHIC组合的测量噪声约为伪距观测噪声的1/2。省略时间参数，卫星位置和钟差作为已知值，对流层延迟用模型计算，线性化的GRAPHIC观测方程为

利用GRAPHIC组合观测量进行精密单点定位的优势是无需利用外部电离层数据进行电离层延迟误差改正。不少学者展示了运用GRAPHIC组合进行单频精密单点定位的效果[11]。

1.4 滤波模型

历元间差分相位观测量可以获得高精度的位置差，GRAPHIC组合可以用于确定接收机的绝对位置，但是其测量噪声约为伪距噪声的一半，为了实现实时精密单点定位，需要综合利用2种观测量，构建的滤波模型为

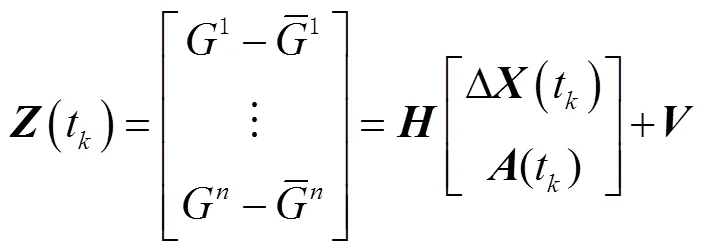
针对以上动态系统，采用Kalman滤波[12]计算卫星位置和钟差的过程如下：

1）状态更新

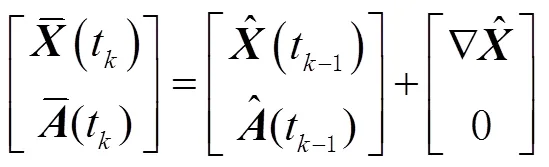
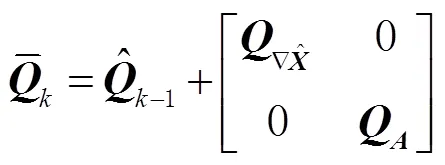
2）观测更新

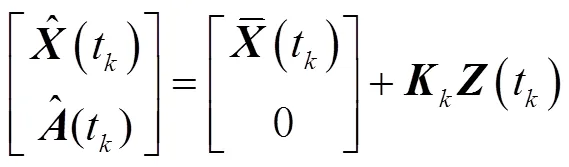
其中

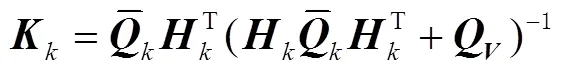
文献[13]采用相似的滤波模型进行低轨卫星的实时定轨，可以获得实时亚米级定轨精度。低轨卫星星载数据的特点是不受对流层延迟影响，电离层的影响也比地面数据小很多，尚未有文献讨论该模型用于地面用户导航定位的可行性。

2 数据处理策略及实现

基于上述原理，本文详细考虑了周跳探测、滤波初始化等问题，开发了1套可用于实时应用的精密单点定位软件。

2.1 周跳探测

周跳探测对于载波相位数据处理十分重要。对于上述方法，如果2个历元之间载波相位发生周跳，则对应的历元差分相位不能用于式（7）进行位置差计算。周跳发生后，在式（15）中要为对应的模糊度参数设置较大的过程噪声，以吸收模糊度的变化。如果不能准确探测出周跳，将会导致滤波发散。对于单频数据，可以通过分析单频伪距和载波相位之差的连续性进行周跳探测。本文采用这一方法实时地探测较大的周跳。在此基础上，在计算历元间位置差时，通过分析历元间差分相位的验后残差来探测较小的周跳，通过多次迭代，每次剔除残差最大的且超过给定限制的卫星，直到没有超限的观测量为止。

2.2 滤波初始化

观测方程式（12）中待估参数包括3个位置参数，1个钟差参数和每颗卫星1个模糊度参数，因此在第1个历元是秩亏的。为此需要进行滤波初始化。本文采用伪距单点定位（single point positioning, SPP）计算初始位置信息和对应协方差阵，用伪距和载波相位求差计算模糊度参数的概略值。

2.3 解算流程

RTKLIB由日本东京海洋大学的高须知二开发的开源程序包，支持多个GNSS系统的标准和定位算法。本文基于开源软件RTKLIB进行2次开发，实现了基于历元间差分相位和非差GRAPHIC观测量的单点定位算法。具体的解算流程如图1所示。

3 实验与结果分析

3.1 实验

为了验证本文的方法，随机选取了2019-05-10（年积日第130天）的4个国际GNSS服务组织（International GNSS Service, IGS）跟踪站（ABMF、CEDU、CHAN和JPLM）采样间隔为1 s的观测数据进行单历元定位实验，测站的分布如图2所示。

图1 软件处理流程

图2 所用测站分布图

为了体现本文方法的优势，进行以下3组实验：

实验1：采用双频伪距进行单点定位计算，采用双频组合方法消除电离层延迟的影响；

实验2：采用单频伪距进行单点定位计算，其中电离层延迟采用Klobuchar 模型计算；

实验3：采用本文所提出的联合历元间差分相位和非差GRAPHIC观测量进行单点定位计算。

以上3组实验中，卫星位置和钟差采用广播星历进行计算，截止高度角为15°，不同高度角的观测量等权处理，伪距和载波相位的观测值分别按照0.3和0.002 m的先验精度进行赋权。接收机位置逐历元解算，每秒钟获得1个位置解。将每个历元的定位结果与已知的精确坐标比较，并转化为东()、北()和上()方向的位置差用以评价定位结果在各个方向的精度。各测站的坐标真值来自于IGS第2052星期的星期解文件。

3.2 结果分析

对于静态观测站，相邻历元间的位置差的理论值为零，因此用式（7）计算得到的历元间位置差可以反映历元间差分相位模型的精度[6]。图3显示了测站CHAN的历元间位置差(d，d，d)序列。可以看出，3个方向的位置差均在±2 cm以内。统计表明、和方向位置差的均方根（root mean square, RMS）分别为0.21，0.29和0.31 cm。

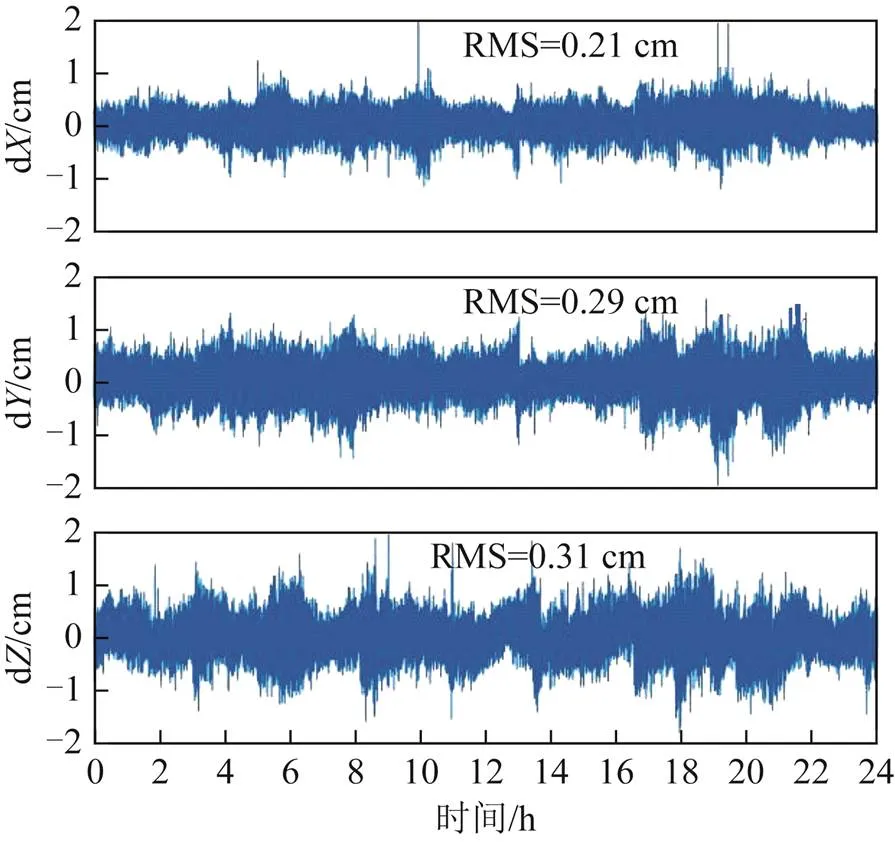
图3 CHAN站历元间位置差序列

图4 实验1：ABMF站偏差序列

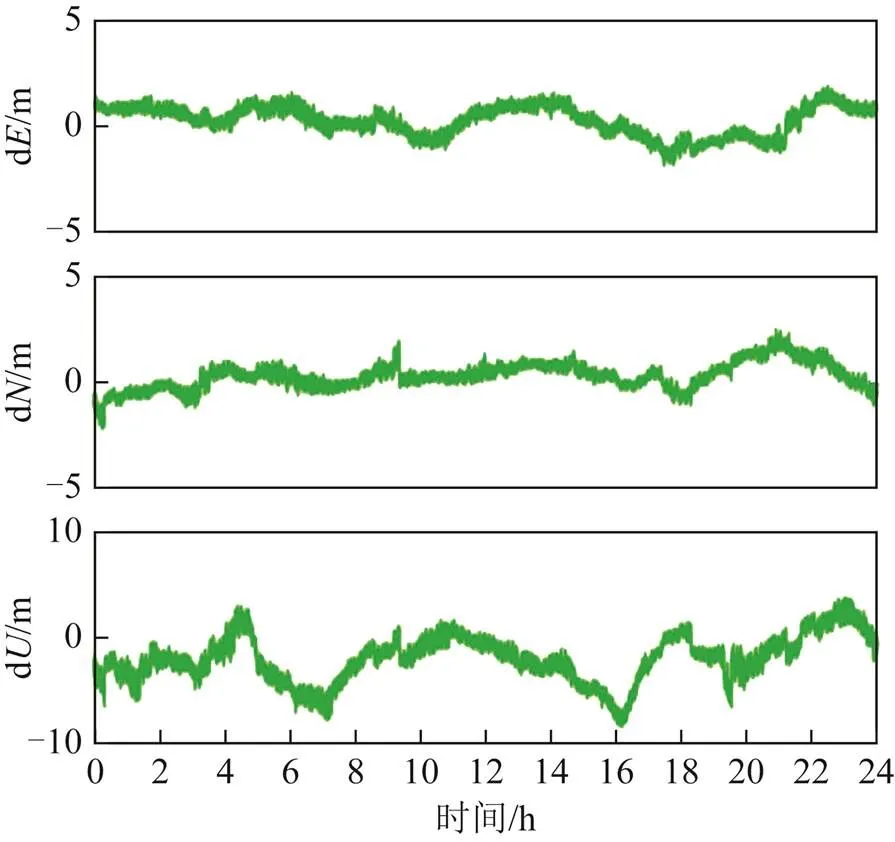
图5 实验2：ABMF站偏差序列

图6 实验3：ABMF站偏差序列和PDOP序列

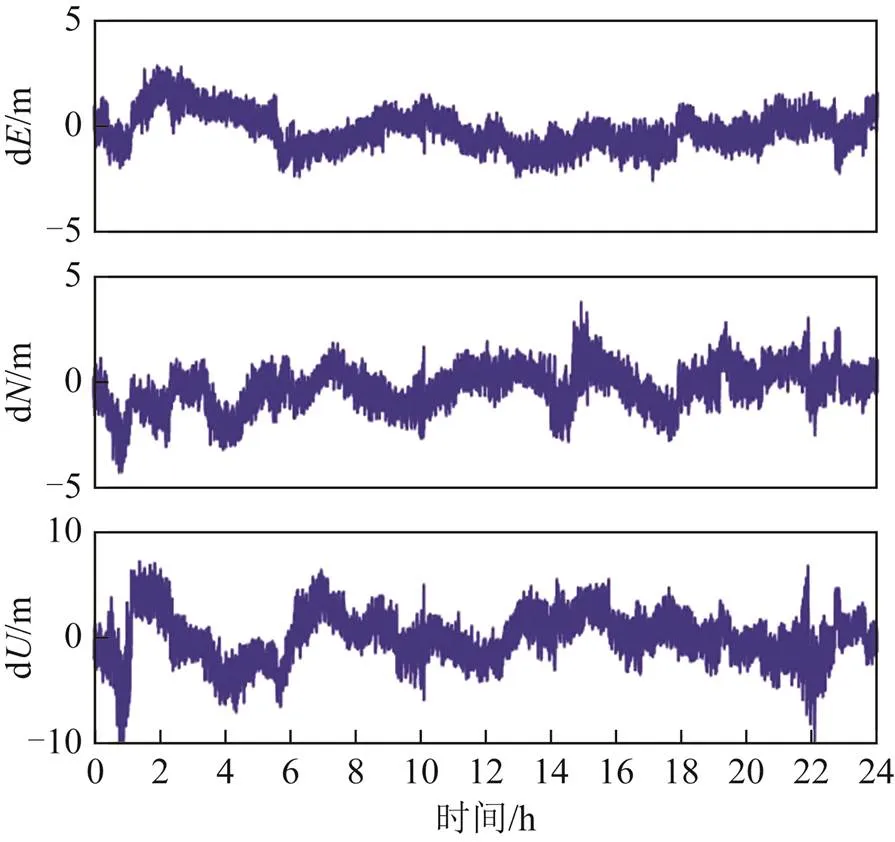
图7 实验1：JPLM站偏差序列

图8 实验2：JPLM站偏差序列

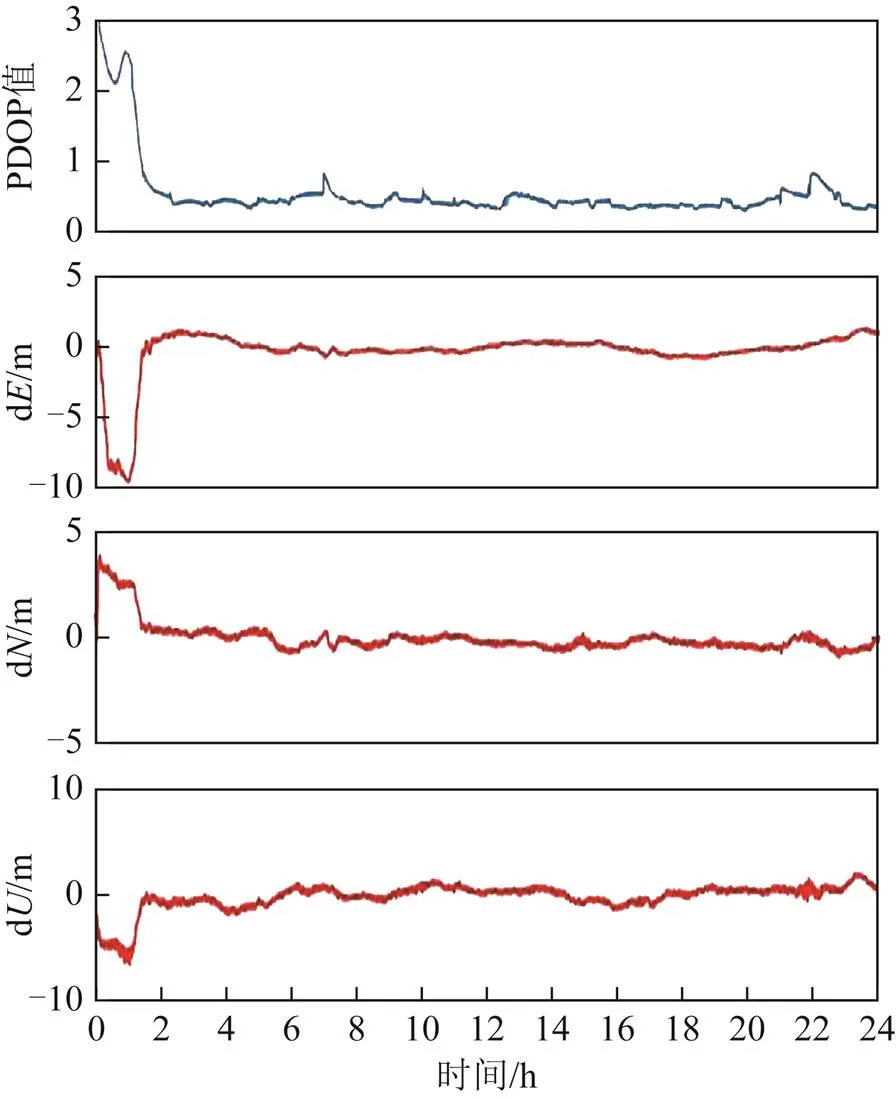
图9 实验3：JPLM站偏差序列和PDOP序列

图10 实验1：CEDU站偏差序列

图11 实验2：CEDU站偏差序列

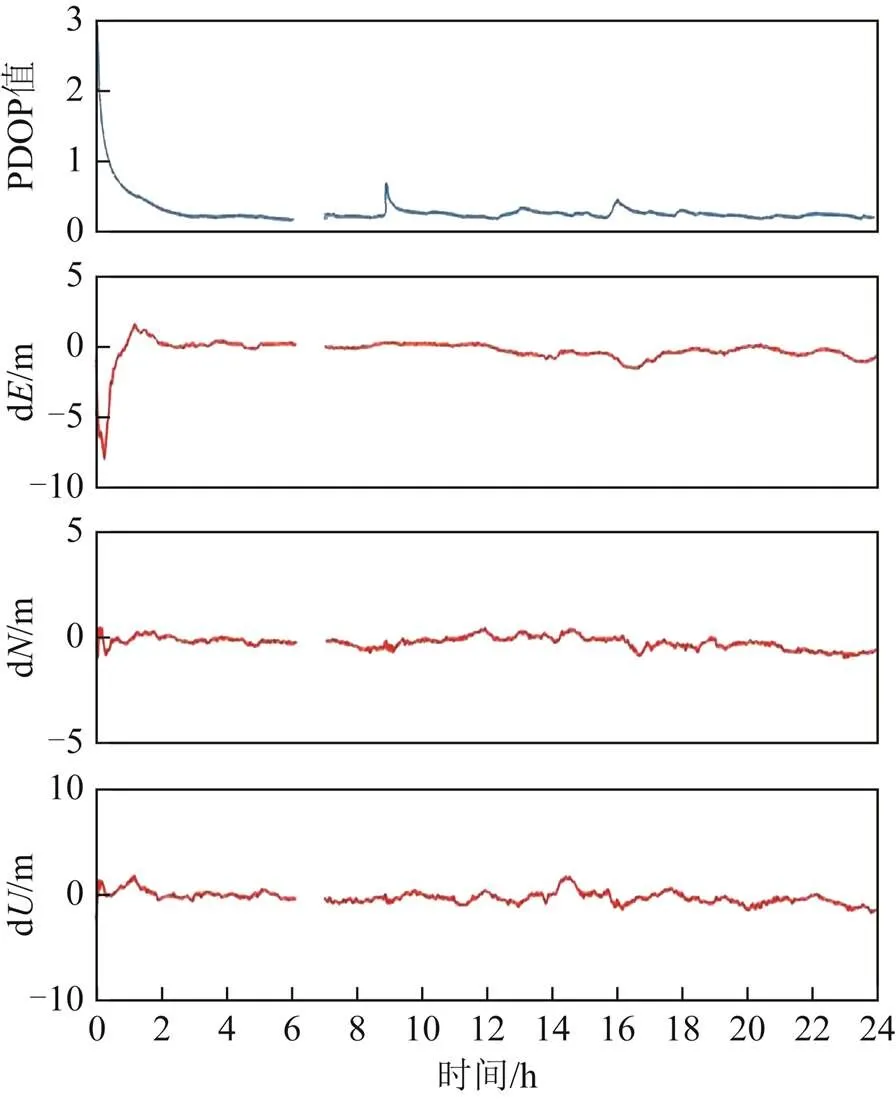
图12 实验3：CEDU站偏差序列和PDOP序列

图13 实验1：CHAN站偏差序列

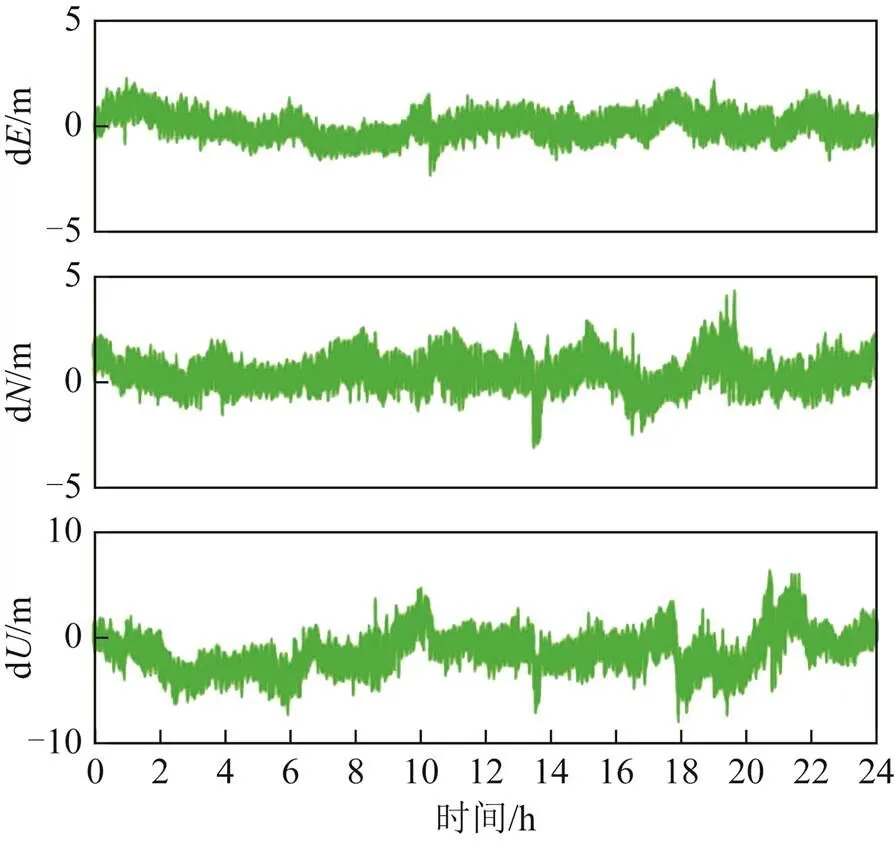
图14 实验2：CHAN站偏差序列

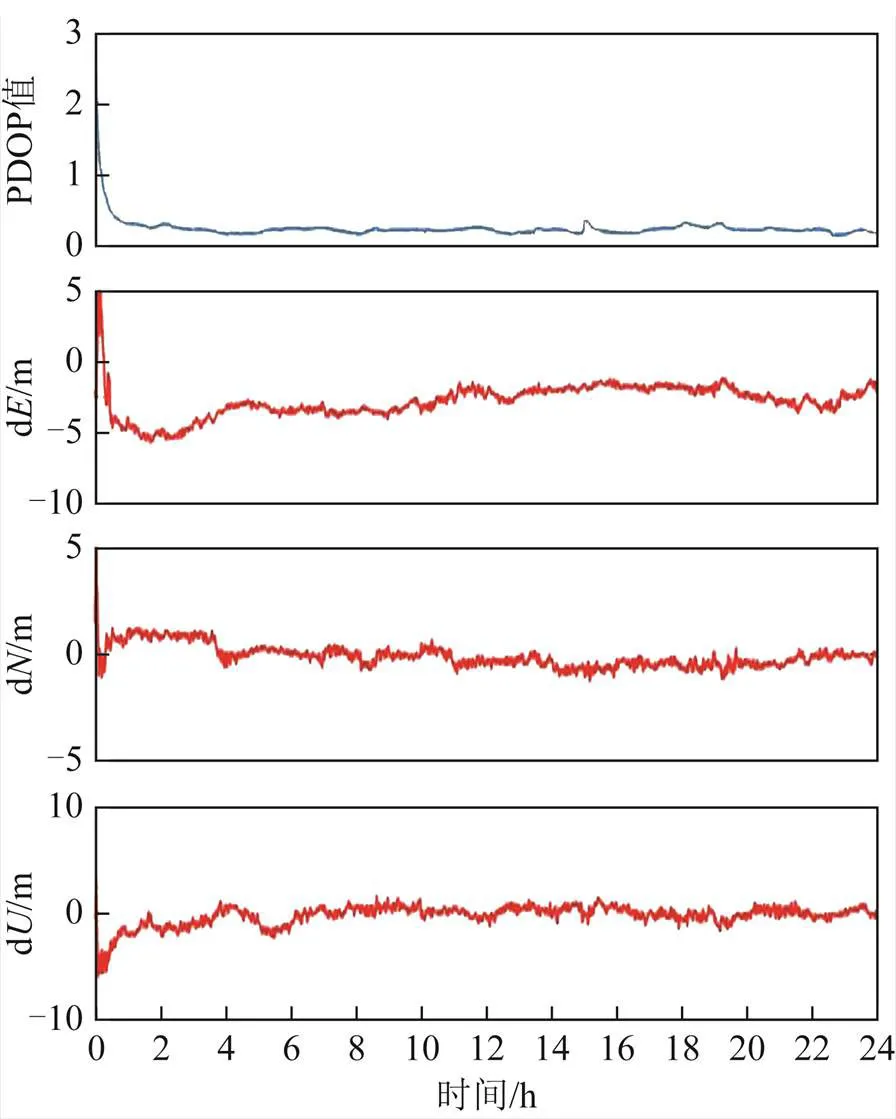
图15 实验3：CHAN站偏差序列和PDOP序列

表1统计了不同方法得到的各测站在、、方向和3维位置（）方向误差的RMS，以及所有测站的平均RMS。其中，实验3的RMS为定位收敛后的结果。可以看出：实验3中各测站方向的RMS都不超过0.71 m ，除了测站CEDU和CHAN外，都优于实验1和实验2的结果；方向的RMS都小于0.5 m，而实验1的都大于0.88 m，实验2的都大于0.67 m；方向的RMS都不超过0.78 m，实验1和实验2的RMS都大于2 m；3维位置（）误差的RMS都不超过1.17 m，实验1和实验2的结果都超过2.2 m。从4个测站的平均RMS来看，实验3在、和方向的定位精度相对于实验1改进幅度分别为43.63 %、70.24 %及74.46 %，相对于实验2改进幅度分别为6.14 %、56.43 %及73.3%。

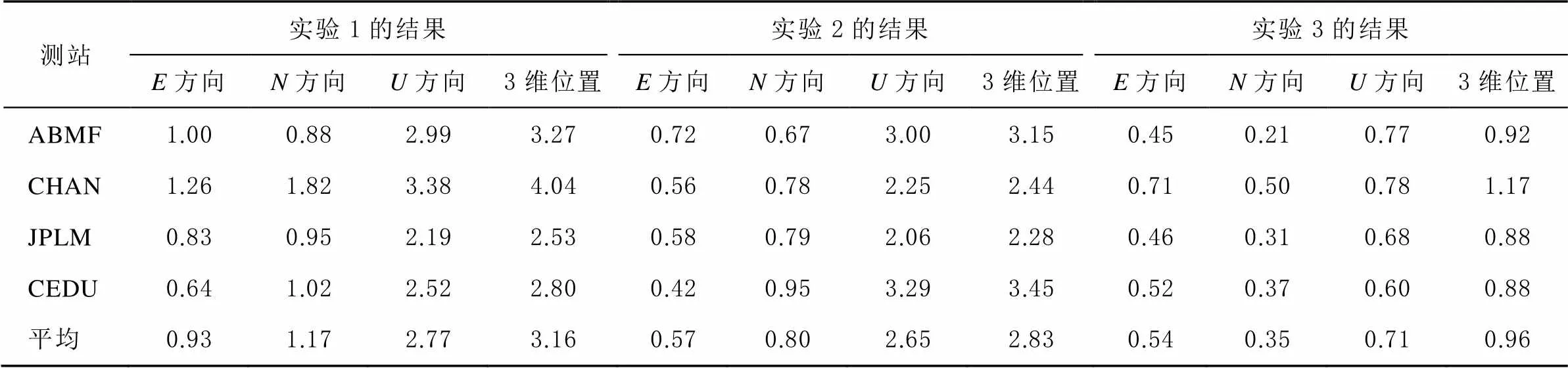
表1 各测站不同实验方法定位误差的RMS统计 m

4 结束语

本文展示了1种基于历元间差分载波相位和非差GRAPHIC观测量的单频精密单点定位方法。该方法的核心思想是利用高采样历元间差分载波相位获得高精度的历元间相对位置差，对GPAPHIC组合获得的绝对位置进行平滑从而提高定位精度。实验表明：滤波收敛之后，该方法在和方向的定位精度（RMS）可分别达到0.54、0.35及0.71 m，在3维位置精度达到0.96 m。与传统单频伪距单点定位方法相比，分别提高了6.14 %，56.43 %，73.3 %；与双频伪距单点定位方法相比，分别提高了43.63 %，70.24 %，74.46 %；与文献[14]相比分别提升了59.39 %，82.41 %，83.41 %。与传统的基于非差相位观测值的精密单点定位方法相比，该方法不需要外部精密轨道、钟差和电离层改正数产品，应用更加方便。

在本文的实验中，不同测站的收敛时间差异较大，下一步将深入分析其原因并设法提高收敛速度。

致谢：本文的研究获得全球连续监测评估系统支持。

[1]刘基余. GPS卫星导航定位原理与方法[M]. 北京:科学出版社, 2008.

[2]张小红, 李星星, 郭斐, 等GPS单频精密单点定位软件实现与精度分析[J]. 武汉大学学报（信息科学版）, 2008, 33(8): 783-787.

[3]李浩军, 王解先, 胡丛玮, 等. 基于历元间差分技术的精密单点定位研究[J]. 宇航学报, 2010, 31(3): 748-752.

[4]TANG Chengpan, HU Xiaogong, ZHOU Shanshi, et al. Initial results of centralized autonomous orbit determination of the new-generation BDS satellites with inter-satellite link measurements[J]. Journal of Geodesy, 2018, 92(10): 1155–1169.

[5]范士杰, 牟春霖, 刘焱雄, 等. 历元间差分精密单点定位的精度分析[J]. 测绘科学, 2016, 41(1): 122-126.

[6]LI Min, LI Wenwen, FANG Rongxin, et al, Real-time high-precision earthquake monitoring using single-frequency GPS receivers[J]. GPS Solutions, 2015, 19(1), 27-35.

[7]彭冬菊, 吴斌.GIM在LEO卫星单频CPS定轨中的应用[J]. 天文学报, 2012, 53(1): 36-50.

[8]MONTENVRUCK O.Kincmatic GPS positioning LEO satellites using lonosphere-free single frequency measurements[J]. Areospace Science and Technology, 2003, 7(5): 396-405.

[9]BOCK H, JAGGI A, DACH R, et al. GPS single-frequency orbit determination for low Earth orbiting satellites[J]. Advances in Space Research, 2008, 43(5): 783-791.

[10]宋伟伟, 施闯, 姚宜斌, 等. 单频精密单点定位电离层改正方法和定位精度研究[J]. 武汉大学学报(信息科学版), 2009, 34(7): 778-781.

[11]阮仁桂, 吴显兵, 冯来平, 等. 星间差分GRAPHIC观测量单频精密单点定位算法[J]. 测绘科学技术学报, 2012, 29(1): 24-27.

[12]杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006: 51-66.

[13]CHEN Pei, ZHANG Jian, SUN Xiucong. Real-time kinematic positioning of LEO satellites using a single-frequency GPS receiver[EB/OL].（2016-11-16）[2019-06-21].https://arxiv.org/ftp/arxiv/papers/1611/1611.04683.pdf.

[14]魏二虎, 刘学习, 刘经南. 北斗+GPS组合单点定位精度评价与分析[J]. 测绘通报, 2017(5): 1-5.

Positioning method using epoch-differenced phase and GRAPHIC observation

YANG Wuzhao1, RUAN Rengui2, SUN Zhongmiao2,3, LIU Ning1, LI Ding1

（1. School of Geology Engineering and Surveying, Chang’an University, Xi’an, 710054, China;2. Xi’an Research Institute of Surveying and Mapping, Xi’an, 710054, China;3. State Key Laboratory of Geo-Information Engineering, Xi’an, 710054, China）

In order to further study on the low-cost, miniaturized and real-time navigation solutions in the industry of general aviation and unmanned aerial vehicle, the paper proposed a single-frequency and single-point positioning method based on differential phase between epochs and group and phase ionospheric correction (GRAPHIC), which could be used in real-time navigation without the information of additional corrections for ephemeris, clocks or ionospheric delays. Finally the method was validated by IGS observatory data, and result showed that: after convergence, the RMS of single-frequency positioning in the,anddirections could be 0.54, 0.35 and 0.71 m, respectively, and the accuracy of the three-dimensional position could reach 0.96 m, which means that the results would be improved by 6.14 %, 56.43 %, and 73.3 %, respectively, comparing with those of traditional single-frequency pseudo-range point positioning; furthermore, the results could be significantly better than those of dual-frequency pseudo-range point positioning.

single-frequency; epoch-difference; point positioning; group and phase ionospheric correction (GRAPHIC); precision

P228.4

A

2095-4999(2020)02-0018-08

杨武召，阮仁桂，孙中苗，等. 联合历元间差分相位和GRAPHIC组合的定位方法[J]. 导航定位学报, 2020, 8(2): 18-25.（YANG Wuzhao, RUAN Rengui, SUN Zhongmiao, et al. Positioning method using epoch-differenced phase and GRAPHIC observation[J]. Journal of Navigation and Positioning, 2020, 8(2): 18-25.）

10.16547/j.cnki.10-1096.20200204.

2019-08-20

杨武召（1994—），男，陕西咸阳人，硕士研究生，研究方向为GNSS精密定位和低轨卫星定轨。