一种基于统计的二维航迹关联方法

魏兵卓，刘 鑫，曹 政，范海洲，杨 刚

（上海机电工程研究所，上海 201109）

0 引 言

多传感器数据融合是指通过相关算法合并来自于多个传感器的数据，进而获得比单一传感器更加可靠、准确的数据［1－2］。在未来军事领域中，该技术是实现网络化协同作战的关键性技术之一［3－4］。航迹关联作为多传感器数据融合的基础和关键环节，其作用是判定来自于各个传感器的航迹是否同属于一个目标。航迹关联的有效性是数据融合正确性的前提和保证。只有关联正确，信息融合结果才会具有准确性、合理性。目前较为常用的关联算法包括双门限法［5］、最近邻法［6］、序贯法［7］等，已经得到了广泛应用。其中，双门限法是指：对来自于两个传感器的L个估计误差样本，逐个进行基于χ2分布的门限假设检验，累计接受M次以上，则完成航迹关联判决［5］，但在实际工程中常常由于多传感器间存在的误差波动导致正确关联率迅速下降［8］。

本文提出了一种基于统计的二维航迹关联方法。该方法首先在统一坐标系下建立了同一时刻不同传感器观测同一目标的位置差距与传感器系统误差、随机测量误差间的函数关系；然后通过计算位置差距的范围设立第一维关联门限，在观测周期内将计算得到的航迹间的位置差距与第一维门限进行比较，建立初次关联；而后进一步计算观测周期内位置差距的方差范围，建立第二维关联门限，并将计算得到的连续时刻内位置差距的方差值与第二维门限进行比较，建立二次关联。在计算关联门限时，本文充分考虑了系统误差和随机测量误差因素，有效克服了传统双门限法在误差波动时出现正确关联率迅速下降的情况。仿真结果表明，相对于传统的双门限法，该方法针对多传感器数据进行关联，具有较高的正确率。

1 位置差距计算

如图1所示，假设编号为s（s＝1，2）的传感器在关联中心北天东直角坐标系OXYZ下位置分别为（xs，ys，zs），某一时刻i分别测得目标的距离、方位角、俯仰角为（Rs（i），As（i），Es（i））。

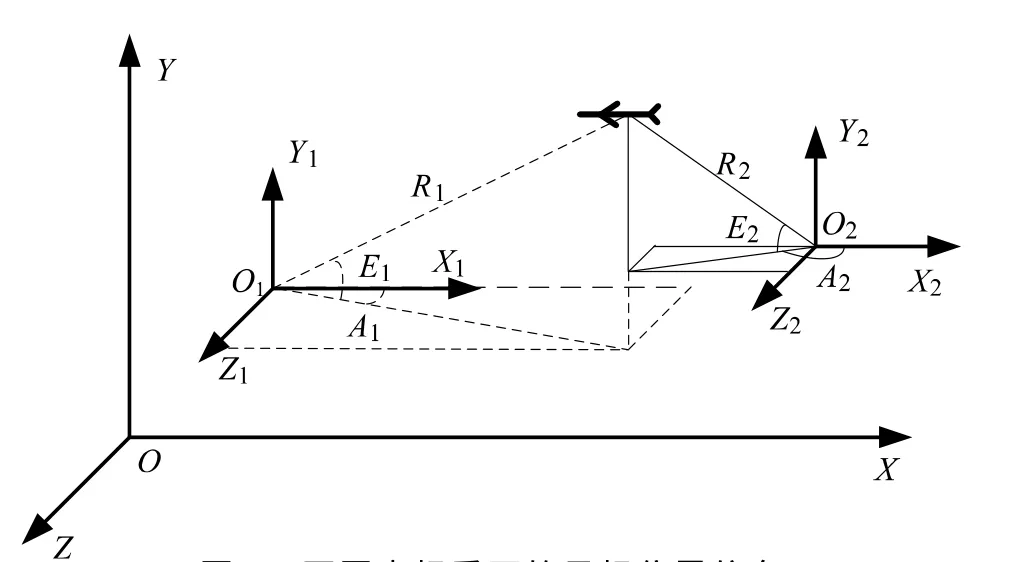
图1 不同坐标系下的目标位置信息Fig．1 Target position information at different coordinates

则在关联中心直角坐标系下目标的位置信息（xT（i），yT（i），zT（i））（T＝m，n）为

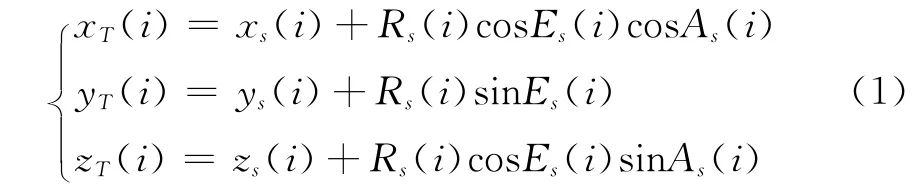
假定目标在编号为s的传感器中真实位置为Ws′（i）＝ ［Rs′（i），As′（i），Es′（i）］T，考虑到传感器探测目标时存在系统误差αs＝ ［αrs，αas，αes］T和随机测量误差βs（i）＝ ［βrs（i），βas（i），βes（i）］T，则记

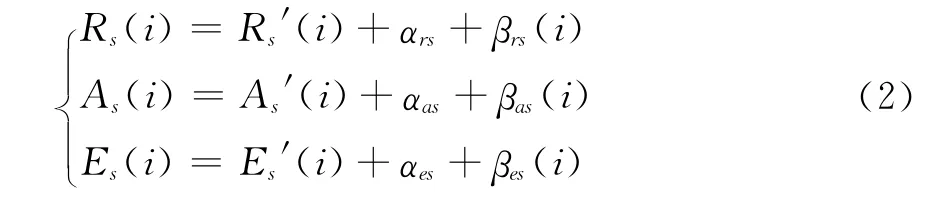
式中：αrs、αas、αes分别为距离、方位角、俯仰角的系统误差；βrs（i）、βas（i）、βes（i）分别为距离、方位角、俯仰角的随机测量误差。假定系统误差的范围已知，随机测量误差服从均值为零的正态分布，则根据式（1）～（2）计算在关联中心直角坐标系下传感器1、2测得的位置差距为

式（4）描述了在坐标系OXYZ下不同传感器观测到同一目标的位置差距与系统误差、随机测量误差的函数关系。

2 第一维关联门限

对于某一具体时刻i，传感器1、2的测量值（R1（i），A1（i），E1（i））、（R2（i），A2（i），E2（i））为确定已知的，可计算出矩阵B（i）中各元素。以X方向上关联门限的计算为例，有

式中：lj（i）为矩阵B（i）中第一列第j个元素；αj为矩阵α中第j个元素；βj（i）为矩阵β（i）中第j个元素。

假设βj（i）随机测量误差中各元素均满足正态分布，即βj（i）～ N（0，），其中为βj（i）的方差。则

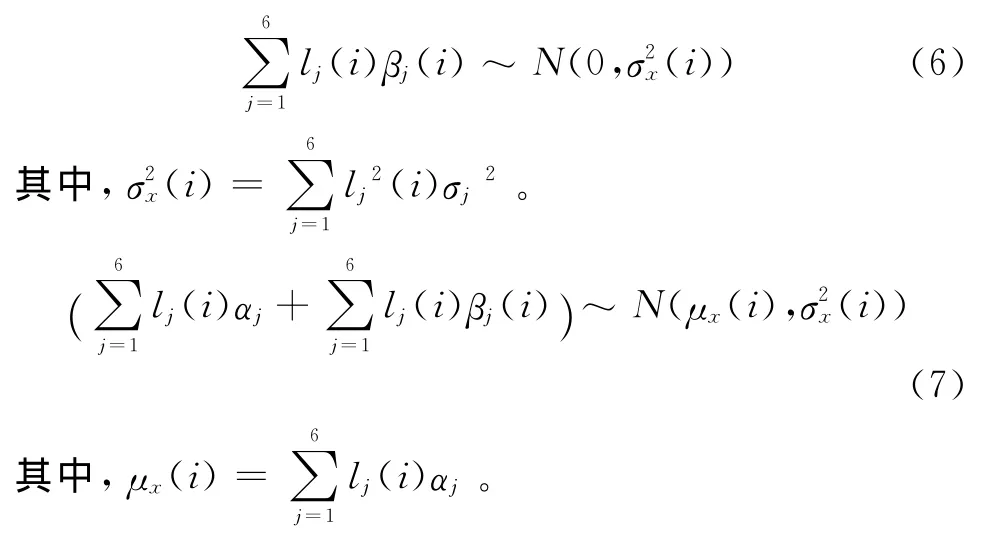
假设系统误差αj的大小范围已知，即αj∈ ［0，αj＿max］（αj＿max≥0）。而由正态分布函数的3σ原则可知（i）βj（i）∈ ［－3σx（i），3σx（i）］的概率不小于99．7%，因此认定其取值范围为 ［－3σx（i），3σx（i）］。由此可进一步估算Δx（i）的取值范围为

则Δx（i）取值范围为

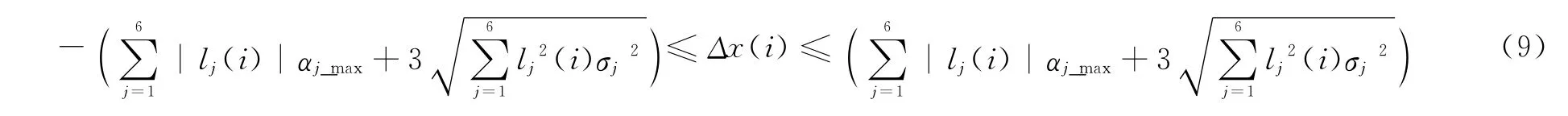
在每个时刻，可根据式（9）计算出Δx（i）的取值范围，当超出该范围时，则认为两个点迹归属于不同目标。依据该范围建立X方向上的初次关联准则：若在连续的M个时刻，来自两个不同传感器的点迹在关联中心直角坐标系下的位置差距均在式（9）计算的范围内，则认为两条航迹在X方向上关联成功。若两条航迹在X、Y、Z3个方向上均关联成功，则认为两条航迹关联成功。

3 第二维关联门限

归属于同一目标的的航迹，其对应点迹间位置差距在连续的时刻内应保持平稳。因此针对初次关联成功的航迹，进一步计算连续M个时刻内位置差距的方差范围来设立第二维关联门限，若方差超出该门限，则认为两条航迹归属于不同的目标。根据式（5），M个时刻内Δx（i）的平均值为

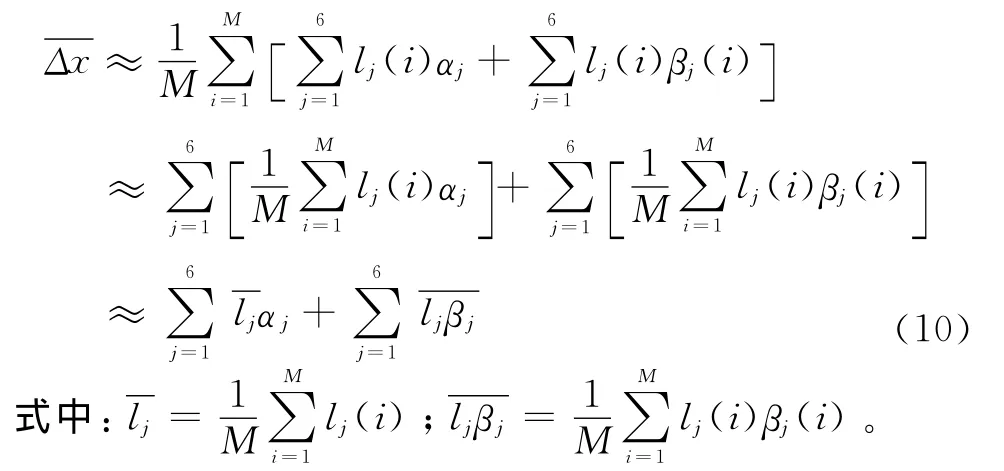
则M 个时刻Δx（i）的方差σ2为

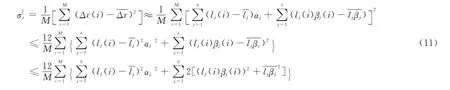
其中，αj∈ ［0，αj＿max］。基于正态分布函数的3σ原则，本文认定βj（i）∈ ［－3σj，3σj］。式（11）中简化为

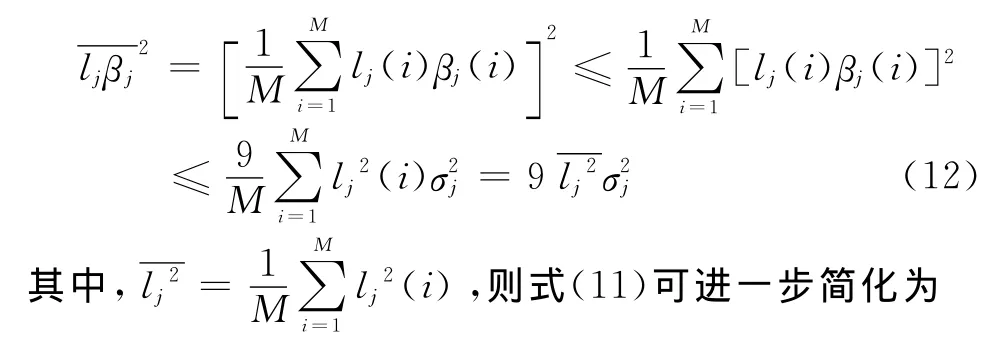
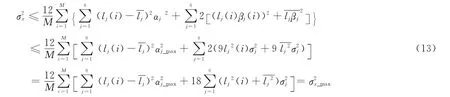
4 仿真分析

为了验证本文算法的有效性，设计了如图2所示的算法流程。

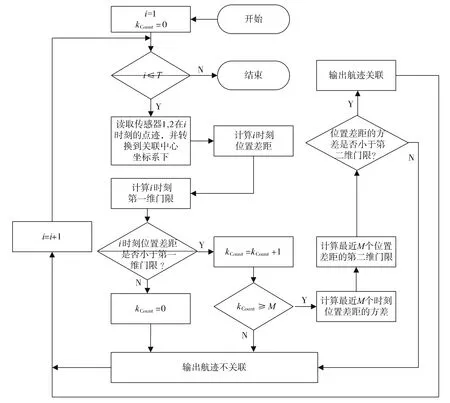
图2 仿真流程Fig．2 Simulation flow

假设本文所有坐标系均为北天东直角坐标系，关联中心坐标系、传感器1和2的观测坐标系原点分别位于 ［0，0，0］、［40 000，1 000，10 000］、［10 000，4 000，40 000］（单位：m）处。传感器1、2观测目标的采样周期均为1s，系统误差设定如表1所示，随机测量误差服从正态分布，标准差设定具体如表2所示。

表1 不同序号仿真过程中系统误差设定值Tab．1 Setting values of system error in different simulations

表2 不同序号仿真过程中随机测量误差标准差设定值Tab．2 Standard deviations of random error in different simulations

空中飞行目标仿真场景设定两种：低密度目标运动场景（图3）和高密度目标运动场景（图4）。模拟低密度目标运动时，传感器1、2探测区域内共有20个飞行目标，其中两批目标间交叉飞行，每批飞行目标6个，目标间平行飞行，间距为250 m，速度为200 m／s，其余8个目标初始位置在探测区域内随机产生，速度方向随机选取，速度大小均为200 m／s。模拟高密度目标运动时，传感器1、2探测区域内共有40个飞行目标，其中四批目标分两组，每组中两两交叉飞行，每批飞行目标6个，目标间平行飞行，间距为250 m，速度为200 m／s，其余16个目标初始位置在探测区域内随机产生，速度方向随机选取，速度大小均为200 m／s。

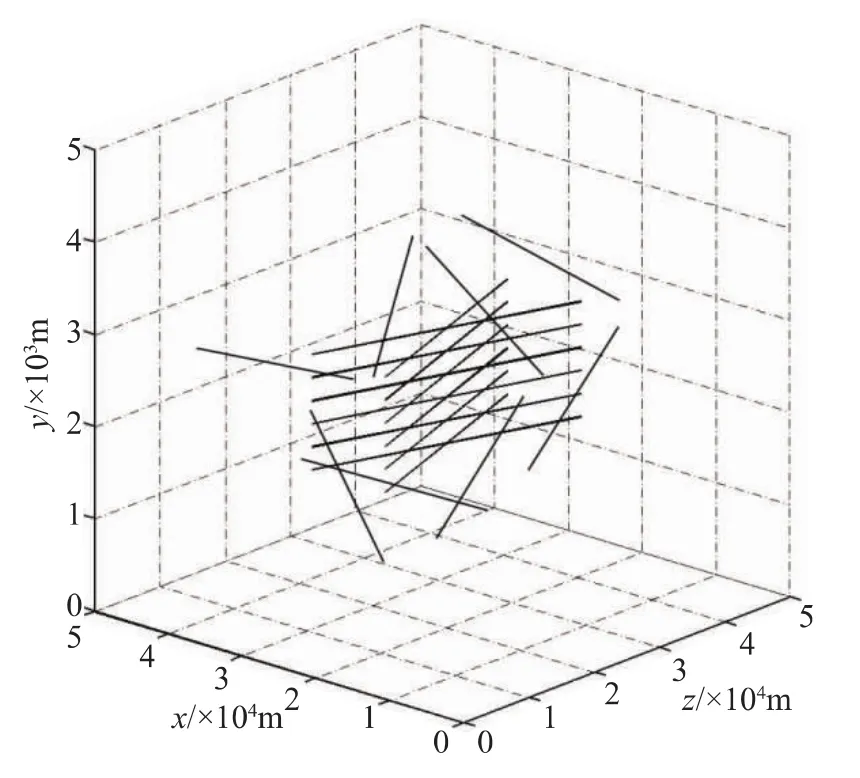
图3 低密度目标运动场景Fig．3 Low－density target motion scene

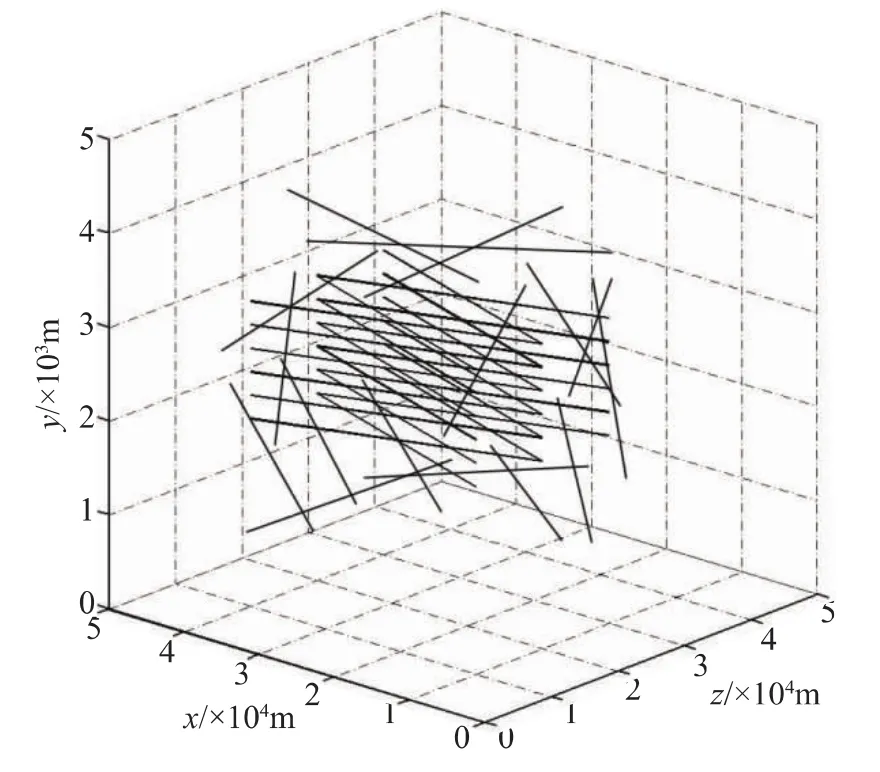
图4 高密度目标运动场景Fig．4 High－density target motion scene

航迹关联有效性的评价主要考虑关联成功概率P1和关联失败概率。P1表示正确判断来自不同传感器的两条航迹归属于同一目标的概率，P2表示没有将归属于同一目标的两条航迹关联成功的概率，且P1＋P2＝1。

针对不同误差情况下（序号1、2、3）的运动场景，采用本文所述的二维航迹关联法、传统双门限关联法分别进行50次仿真，仿真过程中观测窗口M设定为8，结果如图5所示。可以发现，随着系统误差和随机测量误差的增大，两种关联方法的成功概率均出现减小；相较于低密度场景，高密度场景中两种关联方法的成功概率均有所下降。但在设定的不同仿真场景中，二维航迹关联法的关联效果均优于传统航迹关联法。

对序号2高密度运动场景，选取观测窗口M分别为6和10的情况，采用两种航迹关联方法分别进行仿真，结果如图6所示。结果表明，当观测窗口M由6提升到10时，两种航迹关联方法的成功概率均在逐步提升；在不同观测窗口下，二维航迹关联方法均具有更好的关联成功概率。

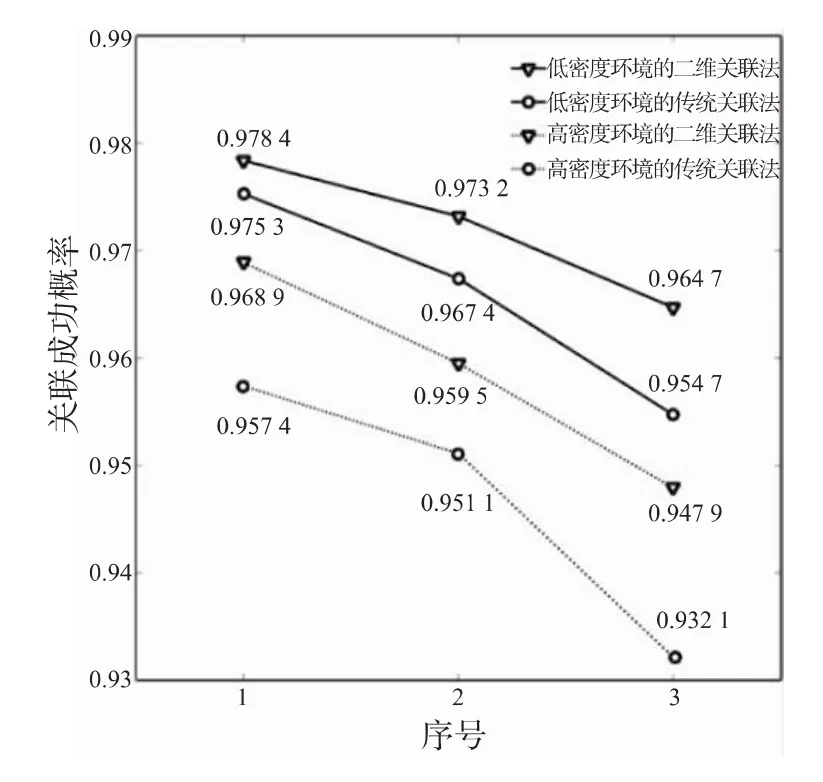
图5 不同仿真环境下关联成功概率Fig．5 Correct correlation rates in different simulation environments

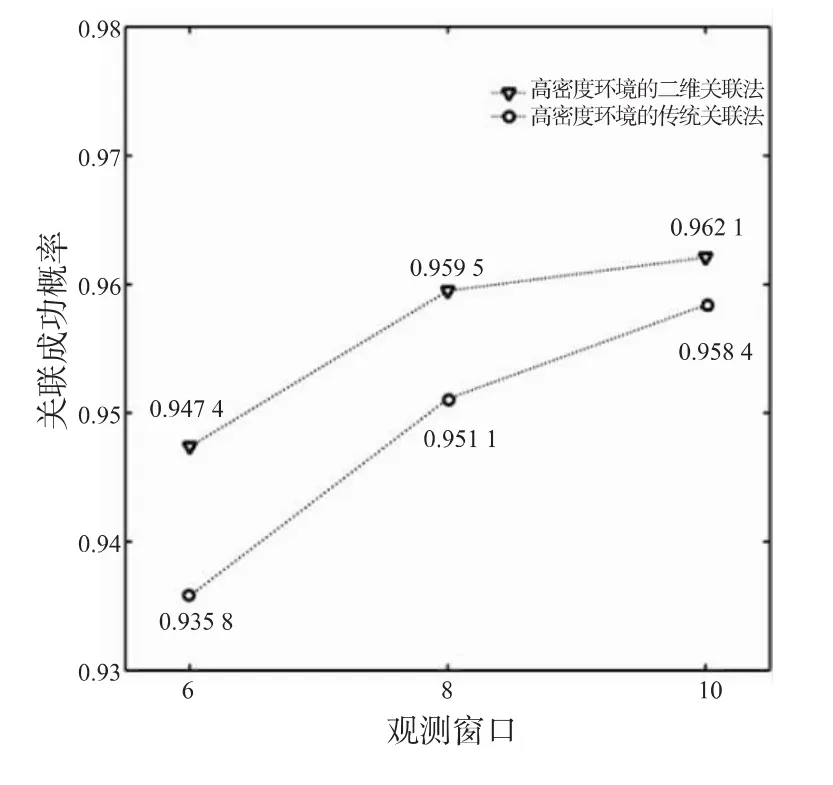
图6 不同观测窗口下关联成功概率Fig．6 Correct correlation rates under different observation windows

5 结束语

本文分析了在统一坐标系下同一时刻由不同传感器观测同一目标的位置差距与传感器系统误差、随机测量误差间的函数关系，并依据该函数关系，进一步估算了位置差距的范围及连续时刻内位置差距的方差范围，建立了航迹间第一维、第二维关联门限。将计算得到的连续时刻内航迹间位置差距与第一维门限进行比较，建立初次关联；进一步将计算得到的连续时刻内位置差距的方差与第二维门限进行比较，建立二次关联。对该算法进行了仿真验证，结果表明，相对于传统的双门限法，该算法在系统误差、随机测量误差增大的情况下仍具有较好的关联成功概率。