高速列车低频晃车在线检测及控制

邓辰鑫，周劲松，夏张辉，宫 岛，孙 煜

（同济大学铁道与城市轨道交通研究院，上海201804）

随着我国轨道交通的迅速发展，高速列车的运行速度、载重和发车频次大幅提升，车辆振动问题日益凸显。低频晃车是高速列车的一种异常振动，对高速列车的运行平稳性和安全性构成了极大的威胁［1］。由于导致晃车的因素众多，如车辆关键部件的性能演变、轮轨磨耗以及外界横风激扰等，目前低频晃车的形成机理［2］尚无统一定论，也没有固定的治理方法。

对高速列车的晃车现象进行在线检测时，检测方法须满足实时性和准确性要求。大部分信号处理方法，如基于傅里叶变换的频域分析等，无法满足实时 性 和 准 确 性 要 求［3］。Huang［4］提 出 了Hilbert-Huang 变换，利用经验模式分解（EMD）把信号分解成若干本征模态函数（IMF）分量，再对分量进行Hilbert 变换，得到时频能量的分布。针对信号局部特征进行分析，从时间尺度入手，获得具有不同尺度特征的IMF分量［5］。该方法的优势在于能提供准确的局部时频特征［6］，并且满足晃车信号在线检测的实时性要求，对指定频段有强分辨力。

检测到车辆发生低频晃车时，启动主动惯容元件吸收车辆的低频振动［7］。Smith［8］提出的惯容器具有能以小质量实现大质量的特性，极大地拓展了悬架的设计思路。文献［9］中给出了惯容器装置，并对其性能展开了试验研究。结果表明，该装置在0.1～30.0 Hz 频率范围内有显著的吸振效果。惯容式动力吸振器目前已在汽车领域得到运用，它能有效地抑制车身共振，显著改善车辆的乘坐舒适性［10］。

基于高速列车晃车的实测振动信号，运用Hilbert-Huang 变换提取实测信号的低频振动能量，并定义谱能比来描述晃车特征，实现对车辆运行状态的在线检测。建立高速列车横向振动模型，利用主动惯容式动力吸振器来吸收晃车的低频振动，并对比控制前后的频响特性和时域仿真结果。

1 经验模式分解和Hilbert变换

1.1 经验模式分解

经验模式分解［4］可将任意信号x（t）分解为

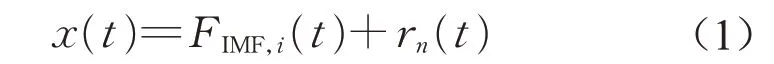
式中：x（t）为原始信号；FIMF，i（t）为第i 个IMF 分量；rn（t）为剩余分量。该方法规定［4］IMF分量中全程极值点和过零点个数必须相等或至多相差一个，并且任意点处极大值包络线和极小值包络线的均值为零。图1 为经验模式分解流程，图中hj（t）表示中间变量。具体分解步骤如下所示：

（1）拟合原始信号x（t）的极大值、极小值包络线u（t）和d（t），取两者均值m（t）作为均值包络线。

图1 经验模式分解流程Fig.1 Flow chart of EMD

（2）x（t）减去m（t）得到低频信号n（t）。重复k次后得到低频信号nk（t），若满足IMF分量规定则作为第1 个IMF 分量；否则，重复步骤（1）和（2）。通常，ε精度下均值为零的条件近似为［5］

（3）令新信号r1（t）=x（t）－FIMF，1（t），并代替x（t）。重复步骤（1）和（2）得到后续的IMF 分量，直至FIMF，n（t）或rn（t）小于阈值、或rn（t）为单调函数或常量。

1.2 Hilbert变换

对IMF分量做Hilbert变换，如下所示：

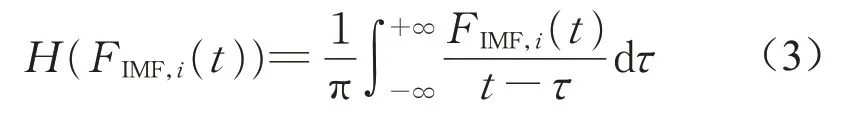
构造解析函数

式中：Ai（t）和φi（t）分别为幅值函数和相位函数。由此得到瞬时频率

并求得原始信号的Hilbert谱和边际谱，如下所示：

2 低频晃车在线检测

2.1 实测数据

以250 km·h-1的运行速度对车辆进行测试，采集该车辆车体横向振动数据，如图2所示。由图2可知，约20 s后出现连续的低频晃车现象。

图2 原始数据Fig.2 Raw data

将整个时间历程分为非晃车段、过渡段和晃车段，分别对非晃车段和晃车段两段数据进行频谱分析，如图3 所示。非晃车段的极值频率出现在0.63 Hz 和1.54 Hz 附 近，晃 车 段则 出 现在0.64 Hz 和1.45 Hz附近。对比第1个峰值，两者的频率接近且晃车段的幅值比非晃车段小32%；对比第2个峰值，晃车段幅值为非晃车段的3倍。从非晃车段到晃车段，车体横向振动的低频能量向1.45 Hz处集中。

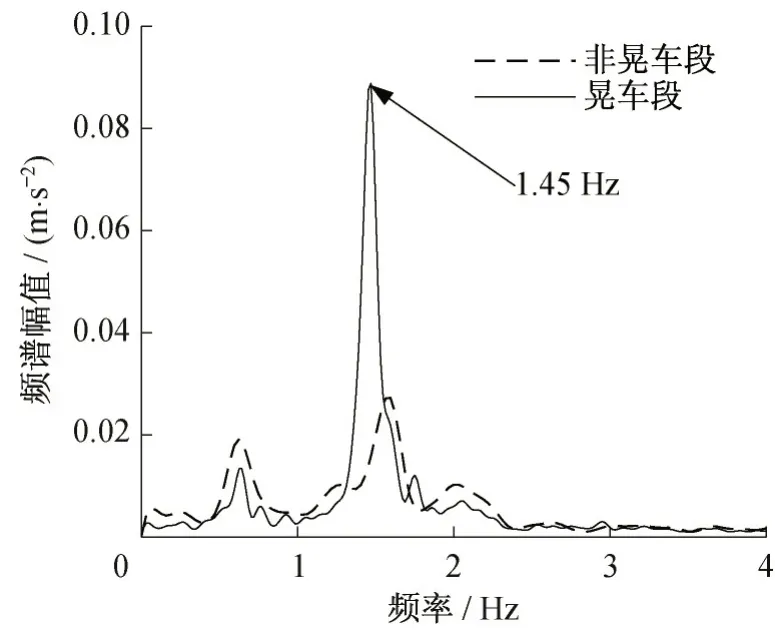
图3 非晃车段和晃车段频谱对比Fig.3 Contrast of spectrum between non- and swaying segment

为了清楚地描述各时段低频成分占整体振动的比例，将0～5 Hz的振动能量占总振动能量的比值记为低频能量比α，即

式中：Sx（f）表示功率谱；fs表示分析频率。功率谱在某频段上的积分表征振动能量。

表1为各时段的低频能量比。不同时段的低频能量比接近，并都处于较高水平。非晃车段和晃车段低频能量比的差值不到10%，分辨力不强。为了保证快速傅里叶变换的频率分辨率，必须基于一定的分析时长，因此不满足在线检测的实时性要求。

均方根值可衡量某时间段内振动水平的高低。图4 显示了整个历程中振动加速度均方根值的变化，计算窗长为1.5 s。非晃车段均方根值总体数值较低；晃车段均方根值存在较大波动，部分与非晃车段接近。因此，均方根值不满足在线检测的准确性要求。

2.2 经验模式分解和Hilbert变换

从晃车段和非晃车段分别选取5 s 时长的样本做经验模式分解和Hilbert 变换，第i 个IMF 分量的能量

表1 不同区段低频能量比Tab.1 Low-frequency energy ratio at different segments

图4 均方根值分布Fig.4 Distribution of root-mean-square value

式中：hi（f）和Ei分别表示第i 个IMF 分量的边际谱和能量。定义第i 个IMF 分量的能量比βi来表征该分量占总振动能量的水平，即

图5 显示了2 个样本前5 个IMF 分量的能量比分布。非晃车段的最大能量比分量为第2个IMF分量，能量比约为46%；晃车段的最大能量比分量为第4个IMF分量，能量比约为51%。

图5 IMF分量能量比分布Fig.5 Distribution of energy ratio of IMF components

图6和图7 分别显示了非晃车段样本和晃车段样本的最大IMF 分量及时频特性。由图6 可知，该分量没有明显的低频振动成分，频率随时间变化的平均值在40 Hz左右。由图7可知，该分量为低频振动成分，频率随时间变化的平均值为1.52 Hz，与图3中晃车段的峰值频率接近，说明该IMF 分量能重现原始信号中的低频振动成分。

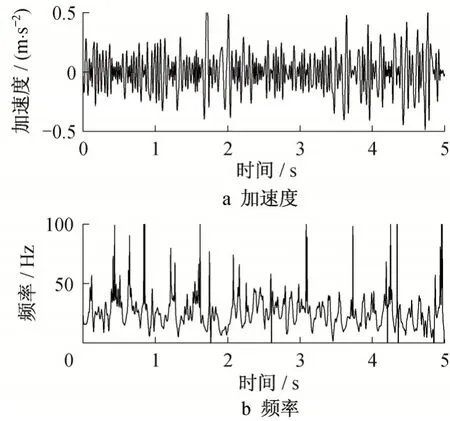
图6 非晃车段样本最大IMF分量及时频特性Fig.6 Maximum IMF component from non-swaying sample and its time-frequency characteristics

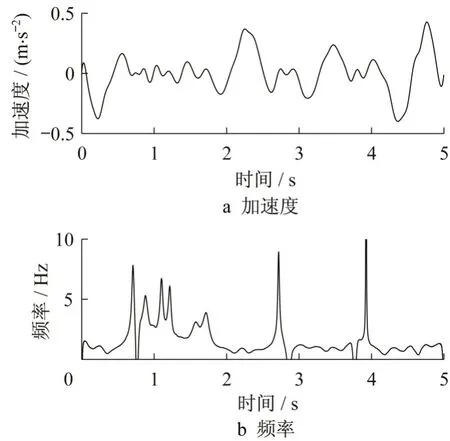
图7 晃车段样本最大IMF分量及时频特性Fig.7 Maximum IMF component from swaying sample and its time-frequency characteristics

与式（10）类似，定义谱能比η 来表征最大能量比分量中低频振动能量占该分量总能量的比例，即

式中：下标m 为最大IMF 分量的序号；Em为该分量的总能量；hm为该分量的边际谱；fs为5 Hz。

选取整个时域样本进行分段处理，各段均为1.25 s。图8 显示了整个时间历程谱能比的变化。在非晃车段，谱能比均较低，最大值为42.18%；在过渡段，谱能比陡升，从26.80%增长到87.30%；在晃车段，谱能比始终较高，最小值为68.37%。整个历程中，非晃车段和晃车段的谱能比波动很小，晃车段的谱能比分布水平始终居高并具有明显的连续性，过渡段存在大幅度的增长现象。处理过程中，各段样本连续且时长短至1.25 s，说明该方法满足在线检测的实时性要求。

图8 谱能比分布Fig.8 Distribution of spectral energy ratio

表2 显示了不同区段谱能比随时间的变化情况。非晃车段的谱能比均值只有25.46%，处于较低水平；晃车段的谱能比均值为81.85%，处于较高水平。非晃车段和晃车段的谱能比均值相差大约55%，说明了该方法满足在线检测的准确性要求。

表2 不同区段谱能比Tab.2 Spectral energy ratio of different segments

3 低频晃车主动惯容控制

3.1 惯容式动力吸振器原理

惯容式动力吸振器是利用惯容器反共振的特性来抑制振动。图9为两自由度并联式惯容器系统。

图9 中，c0、k0、c、k、b 和r 分别表示系统原阻尼、原弹簧刚度、惯容器的附加阻尼、附加弹簧刚度、惯容系数和补偿系数，z1和z2分别为两端的位移。由于附加惯容系统自身具备阻尼元件，可不考虑系统原阻尼，此时频响函数

图9 两自由度并联式惯容器系统Fig.9 Two-degree-of-freedom parallel inerter system

式中：m1和m2为两端的质量；ω 为圆频率。当ω0=时，系统发生反共振，物体振幅为零，据此确定参数k和b。

3.2 高速列车动力学模型及仿真

图10所示为带惯容器的轨道车辆横向动力学模型。

图10 高速列车横向动力学模型Fig.10 Lateral dynamic model of high-speed train

图10中，1处惯容器横移动力学方程为

式中：y、ψ和ρ分别表示横移、摇头和侧滚位移；下标b、t、isd分别表示车体、构架和惯容器；hsc表示车体和构架重心高度差。结合轨道车辆七自由度横向动力学模型［2］，得到整个系统的矩阵方程，如下所示：

式中：轨道不平顺输入Yw=（yw1，yw2，yw3，yw4）T；系统各自由度响应Y =（yb，ψb，ρb，yt1，ψt1，yt2，ψt2，yisd1，yisd2）T；M、C 和K 分别表示质量、阻尼和刚度矩阵，由原模型矩阵［2］扩接形成；D表示不平顺输入的刚度矩阵。上述部分参数如表3所示。

据此，系统的频响函数矩阵

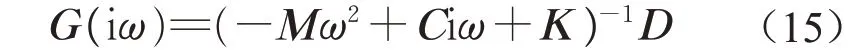
由此计算车辆各处的频响幅值。

图11为车体一位端距纵向中心线0.6 m处的频响函数幅频特性。被动悬挂的车体加速度频响在1.31 Hz频率处出现峰值，该值与前文所述的实测信号频谱中的峰值频率1.45 Hz 接近。当采取主动惯容式控制策略时，车体加速度频响的峰值明显降低，晃车频率处的频响幅值得到了明显抑制，约为被动悬挂时的1/7。

表3 部分参数Tab.3 Partial parameters

图11 频响函数幅频特性Fig.11 Amplitude-frequency characteristics of frequency response function

根据状态空间理论进行时域仿真，选取高速高激扰谱作为轨道不平顺输入，车辆运行速度设置为250 km·h-1。图12显示了不同控制策略下车体一位端的纵向中心线0.6 m处加速度响应。采取主动惯容式控制策略，车体加速度均方根值从0.41 m·s-2降低至0.19 m·s-2，降低了53%。

图12 车体加速度响应时域仿真Fig.12 Acceleration response of carbody from timedomain simulation

4 结论

（1）检测实测晃车信号时，利用经验模式分解和Hilbert 变换定义了谱能比，非晃车段和晃车段车体振动加速度的谱能比相差55%，对晃车的特定频段有着强分辨力，满足在线检测的实时性和准确性要求。

（2）与传统被动悬挂方案相比，主动惯容式车体控制策略显著降低了晃车特定频率处频响幅值，车体振动加速度的均方根值减少了53%。