螺旋面方程建立及铣削时刀具刃型设计*

丁 伟，李春旭，刘柄宏

(1. 辽宁科技大学 a. 应用技术学院，b. 机械工程与自动化学院，辽宁 鞍山 114051； 2. 鞍钢股份有限公司 炼钢总厂，辽宁 鞍山 114001)

复杂螺旋面螺杆广泛应用于气体压缩机、液体泵、挤出机等领域，根据应用场合不同，对螺旋型面有着不同的要求，且随着型面结构日益复杂，对其精度要求越来越高.而螺旋面加工存在易干涉、加工精度不高等问题，严重影响着产品的质量[1-2]，因此对于复杂螺旋面的加工原理、加工刀具设计及干涉问题的研究极为重要.

针对某些螺旋型面用直角坐标系表达相对困难的问题，本文利用标架确定螺旋面方程，然后再将其转换成直角坐标方程，并根据共轭原理设计刀具刃型，运用内铣及合理选择切削用量提高加工精度及效率[3-4].本文提供了母线位于端截面、轴截面、偏轴截面、法截面等各种螺旋型面的数学模型，同时为复杂螺旋面螺杆外、内(旋风)铣削加工提供了刀具设计的数学模型及二分法程序框图.

1 理论分析及螺旋面方程建立

1.1 铣削螺旋面原理

螺旋面铣削过程中，刀具绕自身轴线作回转运动，同时工件绕自身轴线作参数为P的螺旋运动，从而加工出螺旋面.螺旋面铣削坐标示意图如图1所示.

图1 坐标系示意图Fig.1 Schematic coordinate system

图1中，坐标系(o，x，y，z)与工件固连，z为工件回转轴；坐标系(o1，x1，y1，z1)与刀具固连，z1为刀具回转轴，且x1与x重合，y1o1z1面平行于yoz面.铣刀与螺旋面相对运动任意瞬时，工件螺旋面与刀具原始廓面将沿某一空间曲线相切接触，刀具与工件的运动都不影响这条接触线的形状和位置.求出这条接触线且令其绕工件轴线作参数P的螺旋运动，即得到工件螺旋面[5-6]，也就是该接触线与工件固连坐标系(o，x，y，z)中的轨迹.令接触线绕刀具轴线作回转运动，即形成原始刀具面，也就是该接触线在与刀具固连坐标系(o1，x1，y1，z1)中的运动轨迹，求出这条接触线是设计刀具刃型的关键[6-7].

1.2 螺旋面方程

螺旋线方程[8]可表示为ρ=Re(φ)+Pφk.其中：R为基圆柱半径；P为螺旋常数(P=0.5S/π)；S为螺杆导程；e(φ)为圆矢量函数；φ为转角参数.当φ变化时，e(φ)的矢端曲线为一单位圆，i、j、k表示坐标系(o，x，y，z)三个坐标矢量.

在螺旋线上选直角标架{e1，e2，e3}，且使e1=e(φ)，e2=e1(φ)，e3=k.设ξ(t)、η(t)、ζ(t)为母线上任一点在标架上的分量，其中，t为截面角度参数，则母线可表示为ξ(t)e1+η(t)e2+ζ(t)e3，由此得螺旋面方程为

r=Re(φ)+Pφk+ξ(t)e1+η(t)e2+ζ(t)e3=

[R+ξ(t)]e(φ)+η(t)e1(φ)+

[Pφ+ζ(t)]k

(1)

将螺旋面圆矢量函数表达式变换为直角坐标表达式，可得

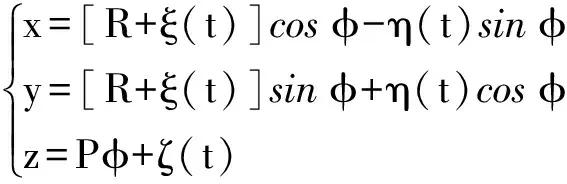
(2)

1.2.1 母线位于端截面情况

当螺旋面母线位于端截面时，母线上任意点在标架e3向的分量ζ(t)=0.由式(1)得此时螺旋面方程为

r=[R+ξ(t)]e(φ)+η(t)e1(φ)+Pφk

(3)

由式(2)得螺旋面的直角坐标表达式为

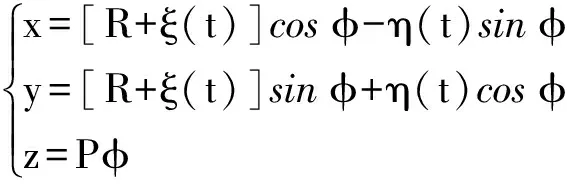
(4)

1.2.2 母线位于轴截面情况

当螺旋面母线在轴截面时，母线上任意点在标架e2向的分量η(t)=0.由式(1)得此时螺旋面方程为

r=[R+ξ(t)]e(φ)+[Pφ+ζ(t)]k

(5)

由式(2)得螺旋面的直角坐标表达式为

(6)

1.2.3 母线位于偏轴截面情况

当螺旋面母线位于偏轴截面时，母线上任意点在标架e1向的分量ξ(t)=0.由式(1)得此时螺旋面方程为

r=Re(φ)+η(t)e1(φ)+[Pφ+ζ(t)]k

(7)

由式(2)得螺旋面的直角坐标表达式为

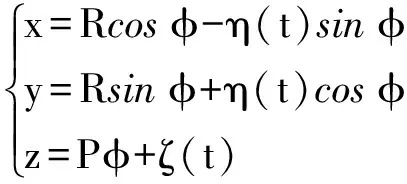
(8)

1.2.4 母线位于法截面情况

当螺旋面母线在偏轴截面在时，选择frenet标架，则有

(9)

式中，β为螺旋角.设ξ(t)、η(t)、ζ(t)为螺旋面母线上任意点在frenet标架上的分量，显然e1向的分量ξ(t)=0.将式(9)代入式(1)得此时螺旋面方程为

r=Re(φ)+Pφk+η(t)e2+ζ(t)e3=

Re(φ)+Pφk-η(t)e(φ)+

ζ(t)[sinβk-cosβe1(φ)]=

[R-η(t)]e(φ)-ζ(t)cosβe1(φ)+

[Pφ+ζ(t)sinβ]k

(10)

将螺旋面圆矢量函数表达式变换为直角坐标表达式，可得

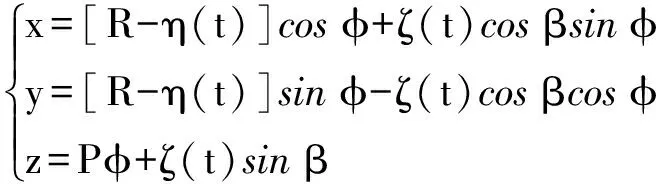
(11)

2 刀具刃型设计原理

只有特定的刀具才能加工出所要求的螺旋面，如上所述，此时刀具和螺旋面在某线上相切，此线即为刀具与螺旋面的接触线.求出接触线，即可得到刀具刃型.

设o1o=a，o1y1对oy转过Σ角，即安装角，两坐标变换关系为

(12)

设G点为接触线F上一点，接触线关系如图2所示.过G作公法线n，由于旋转面上任何法线都与其回转轴线共面，连接Go1，则Go1在n、z1确定的平面上.设n1为此平面的法线，则n1与n垂直，故有

nn1=0

(13)

式(13)即为接触线应满足的向量表达式，即共轭条件式[9].o1在坐标系(o，x，y，z)中的坐标为(a，0，0)，设G点在坐标系(o，x，y，z)中的坐标为(x，y，z)，则o1G坐标为(x-a，y，z)，又知z1坐标为(0，-sinΣ，cosΣ)，因此

Ui+Vj+Wk

(14)

式中：U=ycosΣ+zsinΣ；V=(x-a)cosΣ；W=(x-a)sinΣ.

假设螺旋面的法面截形(即螺旋面母线在法截面内)已知，对式(10)中的φ和t分别求偏导且求外积[9]，可得螺旋面法矢量为

n=(Acosφ+Bsinφ)i+

(Asinφ-Bcosφ)j+Ck

(15)

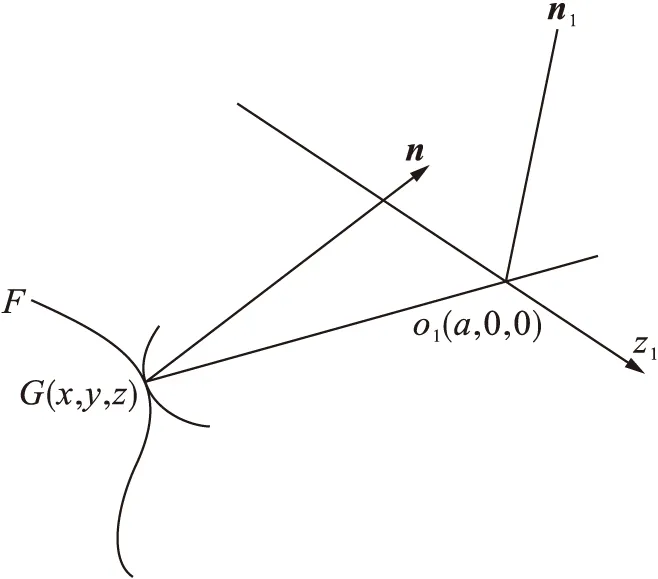
图2 接触线关系Fig.2 Contact line relationship

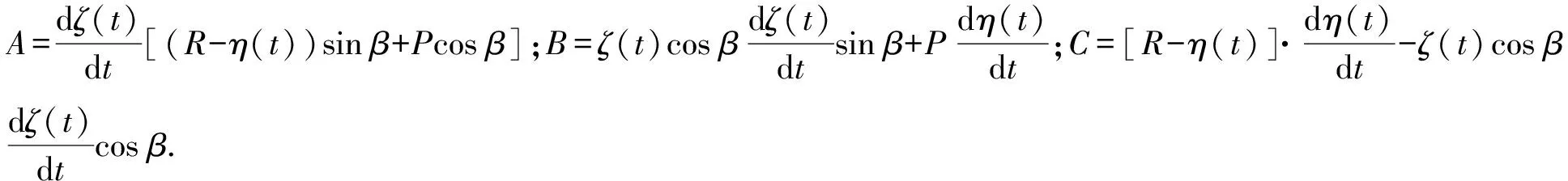
将式(14)、(15)代入式(13)即可确定接触线为

f(φ，t)=U(Acosφ+Bsinφ)+

V(Asinφ-Bcosφ)+WC=0

(16)

式(16)是一个关于φ、t的关系式，一般为超越方程，需用数值法求解.将求得的φ、t代入螺旋面方程，即可得到接触点坐标，进而求得接触线.由于求出的接触点坐标是相对螺旋面上的坐标，需用式(12)变换成铣刀上的坐标值(x1，y1，z1).如令d0为接触点与铣刀轴线间的距离，H为z1轴坐标，把接触点都旋转到通过轴线某平面上，即可得到铣刀加工螺旋面部分轴向剖面的轮廓线，即

(17)

3 设计实例

以某压缩机所用变螺距螺杆为例，建立其中一段螺旋面方程，并设计铣削加工时所用刀具刃型.图3为此段螺杆零件图(单位：mm)，由零件图可知螺杆导程S=72 mm，螺旋常数P=0.5S/π=11.46 mm.图4为螺杆法面截形，法面截形圆弧半径r=12 mm，选取截形圆心至工件圆心为基圆半径，则基圆半径R=33.5 mm，基圆柱螺旋角β=arctg(R/P)=71.11°.

3.1 螺杆螺旋面方程的建立

把法面截形分为三段(bc、cd、de)，分别求出每段所对应的螺旋面方程，具体分段参见图4.

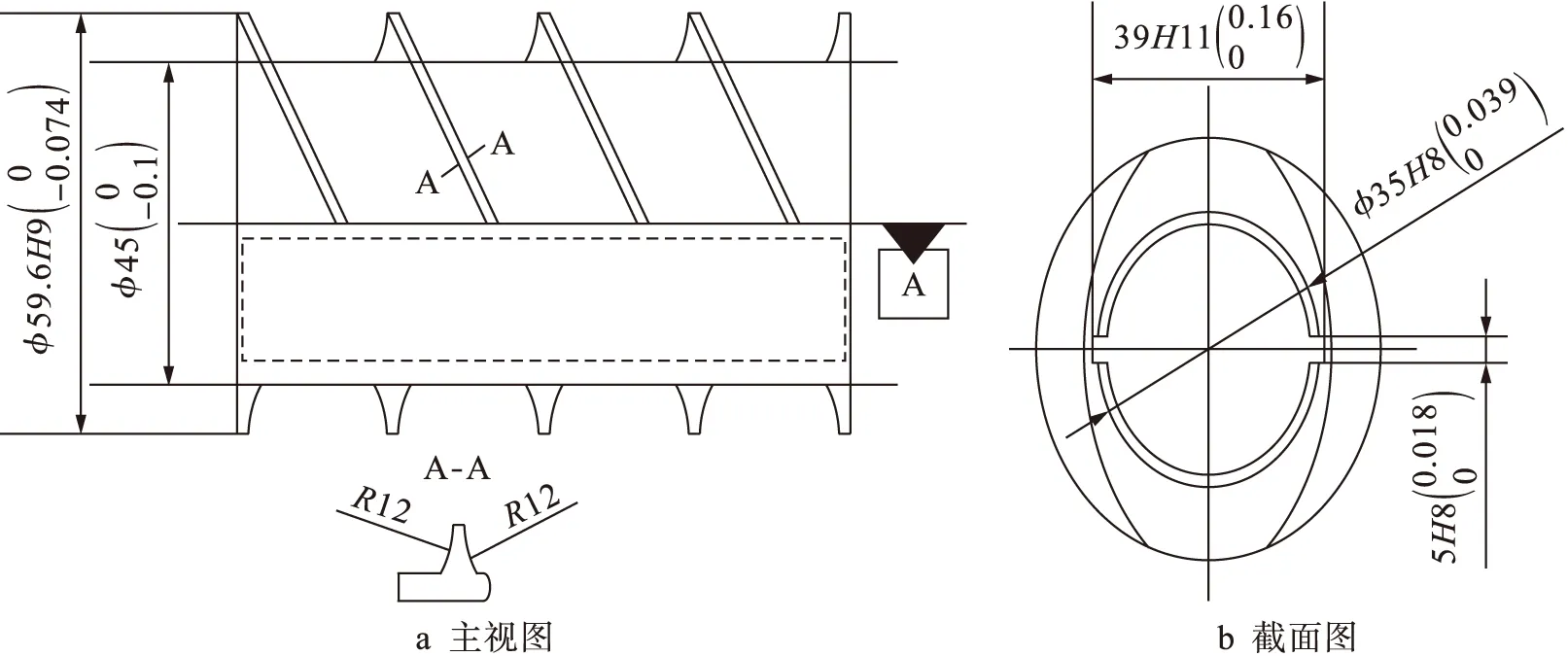
图3 螺杆零件Fig.3 Screw parts

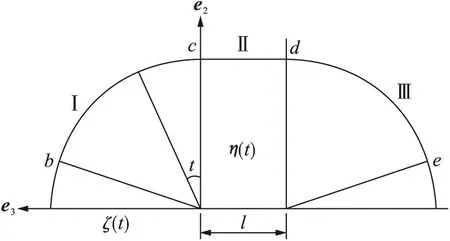
图4 螺杆法面图Fig.4 Normal surface of screw

Ⅰ段：已知η(t)=rcost，ζ(t)=rsint，代入式(10)、(11)得螺旋面方程和其直角坐标表达式分别为

r=(R-rcost)e(φ)-rsintcosβe1(φ)+

(Pφ+rsintsinβ)k

(18)

(19)

此时螺旋面法矢量中各参量表达式为

A=rcost[(R-rcost)sinβ+Pcosβ]；B=rsint(rcostcosβsinβ-P)；C=-rsint[(R-rcost)+rcostcos2β].

Ⅱ段：已知η(t)=r=12mm，ζ(t)=-rtgt，代入式(10)、(11)得螺旋面方程及其直角坐标表达式分别为

r=(R-r)e(φ)-rtgtcosβe1(φ)+

(Pφ-rtgtsinβ)k

(20)

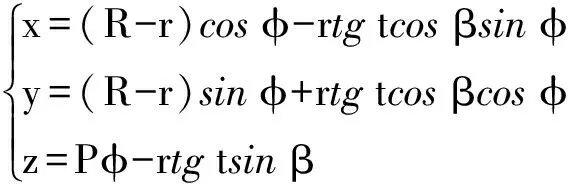
(21)

此时螺旋面法矢量中各参量表达式为

A=-rsec2t[(R-r)sinβ+Pcosβ]；B=r2tgtcosβsinβsec2t；C=-r2tgtcos2βsec2t.

Ⅲ段：已知η(t)=rcost，ζ(t)=l-rsint，其中，l=5.1mm，代入式(10)、(11)得螺旋面方程及其直角坐标表达式分别为

r=(R-rcost)e(φ)+(l+rsint)cosβe1(φ)+

[Pφ-(l+rsint)sinβ]k

(22)

(23)

此时螺旋面法矢量中各参量表达式为

A=-rcost[(R-rcost)sinβ+Pcosβ]；B=rcostsinβ(l+rsint)cosβ-Prsint；C=-rsint(R-rcost)-rcostcos2β(l+rsint).

3.2 刀具刃型设计

3.2.1 螺旋面铣削时安装参数的选取

此螺旋面的截形是由三段光滑曲线组成.只要把螺旋面截形上各特殊点对应的螺旋线映射[10]到特殊平面上，适当选择刀具轴线与工件轴线的距离a及刀具安装角Σ，使刀具轴线与各映射曲线的有效支相交，以满足螺旋面的法线与刀具轴线相交这一共轭条件及不超过共轭界限即可[10].外铣时安装参数选择：a=100mm，Σ=17°；内铣(旋风铣)时安装参数选择：a=-25mm，Σ=17°.

3.2.2 外铣时刀具刃型设计

将每段螺旋面方程x、y、z的表达式及参数A、B、C代入式(16)，即得每段螺旋面所满足的接触条件式.

由f(φi，ti)=0可知，当t0=0时，φ0=0是合理解.以φ0=0为计算的初始值，在整个过程中，前一次的计算结果作为后一次的初始值.由于t是连续的，φ也是连续的，因此以φ0=0为初始值计算出的一系列结果都是合理的.

一般常用于求解超越方程的计算方法是二分法和牛顿法，本文选用二分法.二分法的优点是能充分保证收缩[11]，但它需要预先给出根所在的范围，否则对于每一个确定的ti能从方程中解出不止一个解，但符合需要的只有一个.用二分法确定外铣刀刃型的程序框图如图5所示.

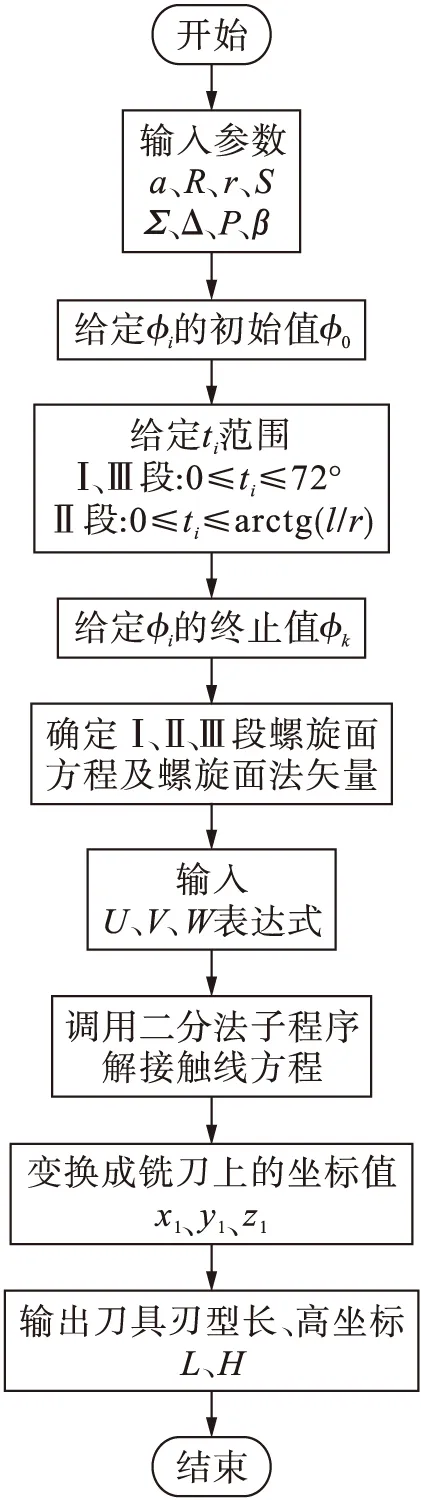
图5 二分法程序框图Fig.5 Program block diagram of dichotomy

图5中，Δ为计算精度，接触线方程的解以φ0表示.在整个计算过程中，前一次的计算结果φ0作为后一次的起始值.当取l=0 mm时，若刀具刃型是半径为r的圆弧，则说明程序正确.图6为对应的外铣刀刃坐标图，图7为对应的内铣刀刃坐标图.

图6 外铣刀具Fig.6 Outer milling cutter

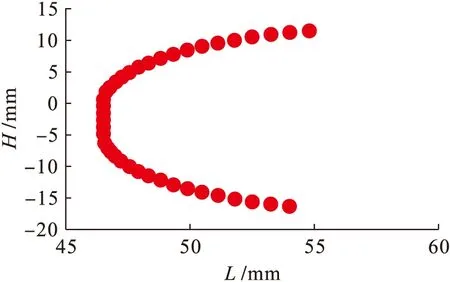
图7 内铣刀具Fig.7 Inner milling cutter

3.2.3 内铣(旋风铣)时刀具刃型设计

内铣时选取的安装参数为：a=-25 mm，Σ=17°.在刃型设计中a按-25 mm代入，其余内铣(旋风铣)时刀具刃型设计方法及程序编制与外铣类似，这里不再赘述.

4 结 论

通过上述分析可以得出以下结论：

1) 以压塑机螺杆为例进行验证，证实了螺旋面方程数学模型及铣刀设计数学模型的实用性；

2) 内(旋风铣)、外铣削螺旋面共轭界限的条件为刀具上与回转圆相切的切矢与加工瞬时接触线切矢共线，超过此界限将会因实体侵入而产生干涉；

3) 在满足共轭条件及不超过共轭界限外，尽量使接触线对应的φ范围最小，使螺旋面形成过程在法面附近完成，以提高加工精度；

4) 与外铣相比，一般情况下内铣(旋风铣)精度、效率更高，但更易产生干涉；

5) 用二分法求解超越方程需给出根的范围，否则每一个确定的ti能从方程中解出不止一个解.