基于升力线理论的风力机气动性能分析方法*
2020-04-11李德源何正举郭坤翔
李德源,何正举,郭坤翔
(广东工业大学 机电工程学院,广州 510006)
80年代Jeng提出升力线算法[9],将叶片用一根环量连续变化的升力线来代替,根据霍姆亥兹涡量守恒定理,从升力线上拽出涡丝张成螺旋尾涡面,即由附着涡(升力线)和尾涡构成流动模型.诱导速度由Biot-Savart定理求解,由涡丝相互之间的诱导考虑有限叶片的效应,不需引入任何修正,是一种简洁有效的算法.
近年来,风力机组呈大型化发展趋势,气动载荷、重力、惯性载荷及操纵载荷随着叶片长度的增加急剧上升[10],需要提高气动模型的三维计算能力.叶片近壁区域流场的展向流动和尾涡系统的三维运动等因素将使基于二维流动假设的BEM模型面临困难,需要对该模型引入人工修正模型,如叶根叶尖损失修正模型和三维无粘延迟失速模型等,才能得出符合实际的结果.而对升力线模型来说,虽然也需要根据二维翼型的升阻力曲线使其计算封闭,但通过Biot-Savart公式计算三维诱导速度在一定程度上提高了该模型的三维流场分析能力,尤其是尾涡模型的引入,大大地增加了模型对尾流分析的可靠性.
基于以上分析,本文采用螺旋尾涡升力线模型来计算叶片气动性能参数.通过对附着涡分布、控制点的诱导速度以及迭代法求解升力系数等问题进行研究和分析,建立了基于螺旋尾涡升力线模型的风力机气动性能数值分析算法,并在FORTRAN平台中创建了分析程序.算例分析了NREL实验室公布的5 MW风力机[11]的气动性能,并与NREL发布的结果进行了对比验证.
1 风力机叶片升力线模型
由伯努利的流体机械能守恒原理可知,由于流过翼型压力面和吸力面的流速不同导致作用在压力面和吸力面产生压力差,从而使翼型产生升力.根据Kutta-Joukowski定理,翼型的升力L可以由自由来流风速w与翼型环量Γ之间的相互作用来表示,即
dL=ρΓwdr
(1)
式中:ρ为当地空气密度;dr为叶片沿展向方向的微段.根据这一思想,升力线模型利用一根涡量沿展向变化的线涡替代叶片,表征叶片与流场之间的相互作用,示意图如图1所示.

图1 涡方法模型示意图Fig.1 Schematic diagram of vortex method model
在升力线模型中,涡量沿展向分布的线涡代表了三维流场中真实三维叶片的附着环量分布,该线涡称为集中附着涡.此外,由Helmholtz第二定理可知,在无粘流体环境中,涡量并不能在流体内部终止,而只能延伸至流体边界或构成环.因此,附着涡沿展向的变化量并不能消失而必然脱落流向下游,形成尾流涡.升力线模型以一根集中涡表征叶片的空气动力作用,对于该集中涡来说,只能感受到力的作用而不能感受到力矩的作用,因此需要将该集中涡放置在翼型的某一点,使得该点的俯仰力矩系数不随攻角的改变而变化,而这样的点恰好为翼型的气动中心[12].
升力线模型通过计算附着涡线上参考点位置处的诱导速度,获取叶片在展向位置某一处的有效攻角,并通过插值获得该处翼型的升阻力系数,从而实现当前翼型的升阻力计算;再通过在整个叶片展向上进行积分,实现叶片的扭矩和功率等气动性能参数的计算.
1.1 诱导速度计算
直线线涡对空间内目标点位置(即控制点)处产生的诱导速度可用Biot-Savart公式描述,即
(2)
式中:wt为叶片控制点处的诱导速度;γ为流场中分布的涡量;r为叶片半径向量;ds为线涡微段矢量.
由于本文采用的是刚性尾涡模型,该涡线为螺旋状,螺旋尾涡向叶片下游延伸至无限远处,形成诱导速度场,坐标系如图2所示.
将螺旋尾涡离散为若干段直线线涡,由式(2)可推出由螺旋尾涡引起的叶片展向位置处的诱导速度,其表达式为

图2 螺旋尾涡示意图Fig.2 Schematic diagram of spiral wake vortex
(3)
式中:s为轮毂中心指向微端dη的向量;wi为叶片展向位置处的诱导速度;r′为轮毂中心指向目标位置点的向量;dη为第k个叶片展向位置r处发散出来的螺旋线涡微段矢量;Γ为附着涡的环量.将dwi沿着坐标轴分解成分量形式,可得
(4)
根据刚性尾涡理论可知,dwx=0.若将诱导速度wi沿着垂直和平行于相对风速w′方向进行分解(如图3所示),则有
dwn=dwzcosφ-dwysinφ
(5)
dwt=dwzsinφ+dwycosφ
(6)
(7)
式中:φ为入流角;V0为来流风速;Ω为叶片转速.

图3 诱导速度分解Fig.3 Decomposition of induced velocity
诱导速度总量可以通过式(5)、(6)从叶片轮毂到叶尖处积分得到.Moriya证明了在叶片上任意位置均有wt=0,设叶片上展向无量纲位置参数为
(8)
式中,R为叶片半径.叶片展向位置任意位置ξ′处,由所有尾涡引起的总诱导速度为
(9)

当θ=θk=0时,积分在点ξ=ξ′处的值变为无穷大,产生奇点,而且奇点附近的积分值也无法确定,为此,本文引进一个额外的参数I,即诱导因子,其定义为
(10)
式中:wn2和wn1分别为涡量强度相同的螺旋线涡和直线涡产生的诱导速度;I为连续函数.
由文献[9]可知,诱导因子I是关于ξ、ξ′和λ0的函数,即
(11)
当θ=θk=0时,积分在点ξ=ξ′处的值同样会变为无穷大,实际上可以近似地认为在这个点处dwn2=dwn1,即I=1,且由于诱导因子为连续函数,可以通过在奇点附近进行样条插值来确定奇点以及其附近的诱导因子的值.
当叶片上各点处的诱导因子确定之后,其诱导速度也可确定,即
(12)
诱导速度与各攻角的关系如图4所示,其中,图4中各变量的表达式为
(13)
(14)
αe=αi+αg
(15)
(16)
根据图4可以得到
(17)

图4 诱导速度与各攻角的关系Fig.4 Relationship among induced velocity and attack angles
设环量为傅里叶正弦级数,并且满足边界条件Γ(ξhub)=Γ(1)=0,则环量函数为
(18)
式中,无穷级数求和可近似用有限项求和来计算,项数m越多,环量Γ(ξ)的计算越精确,一般m取为计算控制点的数目.
根据Kutta-Joukovski定理可知,环量与升力系数之间的关系为
(19)
式中:c为翼型弦长;CL为升力系数.对于每一个有效攻角,均可以通过二维翼型数据表并通过线性插值得到一个与之相对应的升力系数,即CL=CL(αe).
对于初始计算,合成风速w即为来流风速V0,根据式(19)可得
(20)
在小攻角范围内,升力系数与有效攻角之间近似为线性关系,即
CL=a0αe+b0
(21)
式中,a0、b0为常数.综合式(12)、(17)、(18)、(21)可得
(22)
将方程(22)应用于升力线各计算点ξ′处,即可得到M个方程,求解该方程组可以得到Am的值,将Am代入式(18)即可得到环量Γ的值;将式(21)代入式(19),可得有效攻角与环量之间的关系,即
(23)
由环量值即可求出有效攻角αe.
1.2 迭代法求解有效攻角

迭代结束之后,可以计算出叶片的轴向力F、力矩Q以及功率P等叶片气动性能参数,其表达式为
(24)
(25)
(26)
式中,CD为阻力系数,对于每一个有效攻角,都可以通过二维翼型数据表并通过线性插值得到一个与之相对应的阻力系数CD.本文中ψ取为0°.
2 算例分析
根据以上理论分析与数值求解分析方法,在FORTRAN平台上建立了完整的气动性能数值计算程序,实现输入已知参数即可求得多叶片风轮的气动性能参数.
为了验证建立的升力线模型的准确性,以NREL实验室公布的5 MW风力机叶片数据为研究案例,对其气动性能进行计算,并将计算结果与NREL实验室提供的结果(基于叶素动量理论进行的计算)进行对比.
为了保证计算效率和计算结果的可靠性,离散控制点数和位置的选取,一般可根据叶素动量理论计算控制点的选取方法,理论上控制点越多,相应的计算精度越高,但一般不宜取得太多,否则增大了计算量且对精度没有太大提高[9].本文计算中,根据周传捷等[13]的研究可知,将叶片离散为13段,既能保证计算效率,又能得到较为满意的结果.由于叶片靠近轮毂中心的前两段为圆筒状,其升阻力系数在任意攻角下均为恒定值,故其升阻力系数与攻角的函数曲线斜率为0,在进行式(12)的计算时分母为0,会导致结果变为无穷,使得计算无法进行,因此,可以将其剥离出来单独讨论,由于升阻力系数均为已知,故可通过式(24)、(25)直接计算出前两段圆筒的轴向力以及力矩.
基于以上分析,假定前两段圆筒形的环量均为0,则可将叶片第三段起始截面假想为轮毂半径ξhub,因此,叶片的扭角和弦长分布如图5所示.
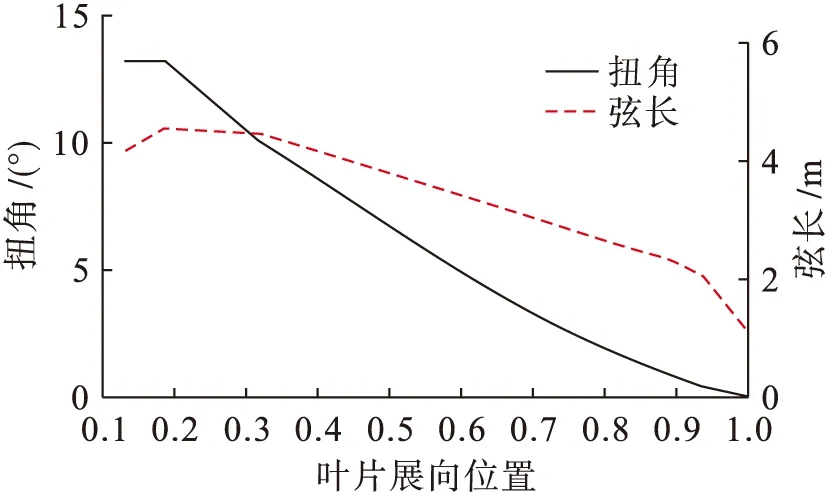
图5 叶片扭角与弦长分布Fig.5 Blade twist angle and chord length distribution
根据NREL公布的5 MW风力机叶片二维翼型数据表[11],各翼型的升力系数曲线的斜率以及截距如表1所示.

表1 叶片各截面位置参数Tab.1 Parameters of blade sections
将上述已知参数作为输入文件导入用FORTRAN编写的升力线模型程序,计算出该5 MW风力机在不同风速下的气动力特性.图6为不同风速下叶片展向位置的环量分布图.

图6 不同风速下沿叶片展向方向的环量分布Fig.6 Distribution of circular rector along blade span direction at different wind velocities
根据文献[11]可知,当风速低于额定风速时,无需对桨距角进行调整,而在更高的风速下,为了使风力机产生稳定的机械功率,在恒定的转速12.1 r/min下需对叶片的桨距角进行相应调整,其相应风速下的变桨距角为文献[11]通过风洞试验所得.表2为不同风速下变桨距后利用升力线模型所求得的风力机轴向力、功率以及扭矩.
将不同风速下采用升力线理论计算所得结果中的推力、功率和扭矩,与NREL实验室公布的5 MW风力机采用引进修正模型的叶素动量理论计算所得的相应参数[11]进行对比,结果如图7所示.
由图7可以看出,用升力线理论计算得到的风力机的功率、力矩、轴向力与文献[11]基于修正的叶素动量理论计算结果比较接近.通过NREL实验室公布的5 MW风力机叶片计算案例可以看出,风力机叶片气动性能参数的升力线模型具有较高的准确性.
3 结 论
本文采用基于螺旋尾涡的升力线模型来研究风力机三维流场的空气动力学性能,研究了升力线模型中附着涡分布和诱导速度的计算,并通过对升力系数进行迭代收敛来修正环量,从而确定准确的攻角和升阻力系数,进而计算出风力机的各项气动性能参数.值得注意的是,诱导速度的求解考虑了风力机各个叶片之间的相互诱导效应,因此,相比于叶素动量理论而言,升力线理论可以极大提高风力机的三维计算能力.
基于升力线模型的理论基础,本文建立了风力机叶片的升力线数值计算模型,编译了适用于多个叶片风轮的气动性能参数分析程序,并与NREL实验室公布的基于叶素动量理论的5 MW风力机气动性能参数进行对比,结果表明,基于螺旋刚性尾涡模型的升力线算法通过结合翼型的升阻力特性可以有效计算风力机的气动性能参数,而且无需引入应用叶素动量理论时需要的大量人为修正模型即可以满足工程要求的精度.对于叶素动量理论而言,人为引入模型的不同可能会导致计算结果存在一定偏差,而升力线模型由于无需引入各种修正模型,减少了繁琐的模型引入,相对于叶素动量理论和CFD理论而言,其计算效率也会提高,同时也可以在一定程度上保证计算的稳定性.由于升力线理论考虑到了叶片展向之间的流动,其不仅适用于直叶片,对于积叠线弯曲的、三维流动更强的叶片(如后掠叶片)设计与气动性能计算同样有效,并能与叶片结构模型结合进行高效而准确的气弹耦合分析.
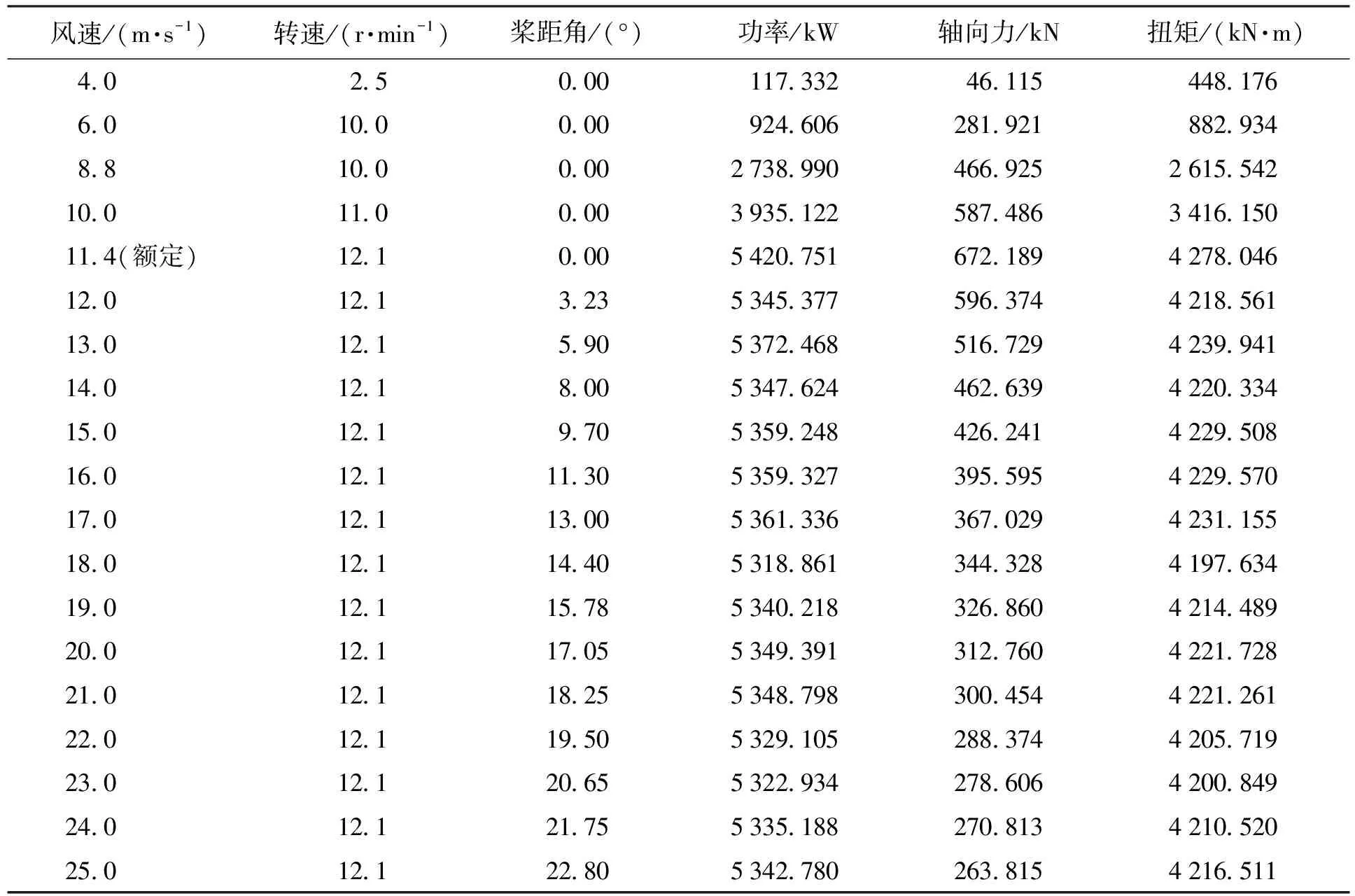
表2 不同风速下风轮气动性能计算结果Tab.2 Calculated results of aerodynamic loads of wind turbine at different wind velocities

图7 不同风速下两种理论计算结果的比较Fig.7 Comparison between two theoretical calculation results at different wind velocities
